A Sort of fusion control strategy for uncertainty complex process with large time lag*

Bo BI

International School, Chongqing Jiaotong University，Chongqing 400074，China



A Sort of fusion control strategy for uncertainty complex process with large time lag*

Bo BI†

International School, Chongqing Jiaotong University，Chongqing 400074，China

Abstract:Aiming at the puzzle of being lower in control precision of complicated large lag process resulted by uncertainty, the paper presented a sort of control strategy based on algorithm fusion. In the paper, it studied the control puzzle and cybernetics characteristic, based on the complex process characteristic with large lag, fused that the integral control is propitious to eliminate the steady error, Smith estimator control is helpful for time lag compensation, and fuzzy control is conducive to deal with some uncertainty controls. Based on the integration of their respective advantages, it gave a sort of I-Fuzzy-Smith control algorithm. Based on MATLAB simulation, it took the inertial process with large time lag as an example, and conducted the comparative study respectively by PID, Fuzzy-Smith and I-Fuzzy-Smith control, and the response demonstrated that the fusion control strategy would be more advantages in respect of system dynamic & static performance and robustness than others. The research result shows that the proposed fusion control strategy is high in control precision, and shows very strong robustness.Key words: Fuzzy control, Smith estimator control, Integral control, Fusion based control strategy

1.Introduction

It is difficult to build the mathematical model for uncertainty complex process with large tine lag, and therefore it is the puzzle of control engineering. Despite the fuzzy logical control owns the peculiarity without the accurate mathematical model of system, and it is simple in algorithm implementation, but the fuzzy always exists in steady-state error, and it would be much worse in control effect for large time lag system. If it takes the nonlinear characteristic of relay into account, then the system is very easy to produce the oscillation[1]. Smith estimator control is considered as one of the most effective control strategy to overcome the impact of large time lag process, but it is very sensitive to the model error. When the model error gets large the quality of Smith estimator of compensating control system would be deteriorated, and even the stability would be lost[2-4]. Going so far as to the discussion about uncertainty, here it is only limited to the uncertainty of being subordinated by the statistical law, such as the uncertainty of general fuzzification. Aimed at the respective superiority, the Smith estimator control can effectively conduct to compensate the impact of time lag for fuzzy control system, and the introduced integral node is propitious to eliminate the steady-state error of the system, and the fuzzy control can deal with the uncertainty puzzle with fuzzification. Based on the above mentioned, the following explored the control strategy with fusion control algorithm.

2.Control puzzle of complex system

The control puzzle comes from the unpredictable cybernetics characteristic of complex process. The complex process always showed the following characteristic from different hierarchy in different respects. For example, it is sometimes unknown, time-varying, randomness and dispersion in system parameter, the system time lag is also unknown and time-varying, there is the serious nonlinearity in system and the relevance among system variables, and in external environmental disturbance there are the unknown, diversity and randomness. Due to the uncertainty in control, the conventional control strategy such as PID controller is incapable of action. For uncertainty control puzzle, the conventional control method is very difficult to build the mathematical model, but the conventional control is essentially a sort of numerical computing method, and it is very high to be demanded by structured control degree, and therefore it is not feasible to adopt PID control because of the complex system being unstructured or semi- unstructured. The complex process is always highly non-linear, and the control method is complicated unnecessarily, and so it makes the traditional control strategy be incapable of action. The relation among sub-process is complicated and confused, and it is highly coupled between the factors and restricted mutually. In addition, the external engineering is very complicated, and the conventional control strategy is lack of effective solution. There is often a contradiction between the robustness and sensitivity for the conventional control method, and it is probably caused to the entire control system collapse for the change of some conditions. The above characteristic is the control puzzle of complex process, and in order to make effective control it is necessary to explore more effective control strategy from cybernetics hierarchy.

3.Control strategy based on algorithm

A general model structure of negative feedback control system is shown as in Figure 1, and the solving space of control problem is constituted by the system deviation and its change rate as well as timet. In Figure 1,r(t) is the system input,u(t) is the output of controller,y(t) is the output of system, ande(t) =r(t)-y(t).

Figure 1.Structure of negative feedback control system

According to the actual process characteristic, it can select the controller matched with the process characteristic. In this paper, it is selected to the control strategy based on fusion of integral control, fuzzy control and Smith estimator control. The priority of the strategy is that it exerted the advantages of Smith estimator control which can overcome the impact of large time lag. Here it assumes the controlled process transfer function with pure time lag to be asW0(s)e-τs, and the transfer function of controller to be asWc(s), then the structure of conventional Smith estimator control system is shown in Figure 2.

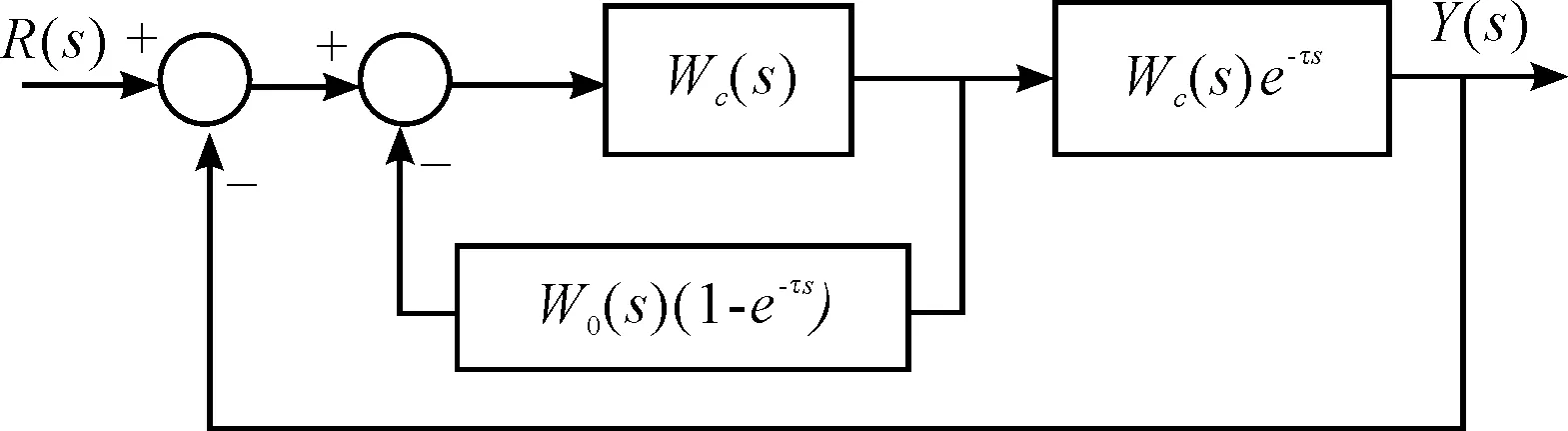
Figure 2.Smith control system structure

From Figure 2 it can be seen that it makes the connection in parallel between the controller and compensation linkW0(s)(1-e-τs), and the compensation link is called as Smith estimator. The system transfer function is as the following.

W(s) =Wc(s)W0(s)e-τs/(1 +Wc(s)W0(s))

FromthetransferfunctionW(s) it can be seen that it is without pure time lag nodee-τsin the characteristic equation after the system compensated, and therefore it realized the complete compensation for controlled process time lag, and improved the adverse impact of pure time lag for controlled process. As for thee-τspure time lag term in expression, it only delayed a timeτfor response curve of control process.

Due to the fuzzy control being not dependent of accurate math model system, the realization of control algorithm is correspondingly simple, and here it is omitted. The introduced integral node can eliminate the steady-state error, and improve the control quality. The Smith estimator control can overcome the impact of large time lag. Based on the fusion of the three advantages, it is easy to construct the simulation model of integral, fuzzy and Smith estimator control algorithm.

4.Control simulation model

In automation control process of industrial production, the most process model can be approximatively viewed as a first order model, second order model, first order plus time lag model and second order plus time lag model respectively aimed at the different situation[5]. Aimed at the uncertainty complex process with large time lag, such as temperature control of plastic & rubber vulcanization process etc, it has the characteristic with nonlinearity and large time lag, and here it can be described by a inertia node plus a large time lag node, namely the transfer function is as the following.

W(S) =Ke-τs/(Ts+ 1)

Inwhich,Kis the amplification coefficient,Tis the time constant of system,τis a pure time lag. By means of the frequently-used step response method, it is easy to determine the parameterK,Tandτ[6]. Here it takesK=0.83，T=1 680 s，τ=200 s. Then the approximate model of the temperature object is as follows.

W(S)=0.83e-200s/(1 680s+1)

UndertheconditionofMATLABenvironment,bymeansofSimulinktoolbox,itcanbuildthesimulationmodelofsystem,andunderthestepinputsignalitconductsthesimulationofcontrolsystem.

5.Simulation of control algorithm

Forconveniencetomakethecomparison,thesamecontrolledobjectisrespectivelycontrolledbyPIDcontrol,Fuzzy-SmithcontrolandI-Fuzzy-Smithcontrol,andhereitisomittedtothecontrolstructurediagrambecauseofbeingnotdifficulttoconstruct[7-8].TheresponsecurveofthreecontrolmethodsisshowninFigure3.Thecurve1istheresponsebyPIDcontrol,andthecurve3istheresponsebyFuzzy-Smithcontrol,andfinallythecurve2istheresponsebyI-Fuzzy-Smithcontrol.Comparedwiththreeresponsecurves,itcanbeseenthatthePIDcontrolhasa40%overshoot,andforFuzzy-Smithcontroltherisetimeis3 600sandthereisasteady-stateerrorof0.5,andfinallybyI-Fuzzy-Smithcontroltherisetimeis260sandthereisnosteady-stateerrorandovershoot.ThereforeitcanbeseenthatI-Fuzzy-Smithcontrolownsbettercontrolquality.

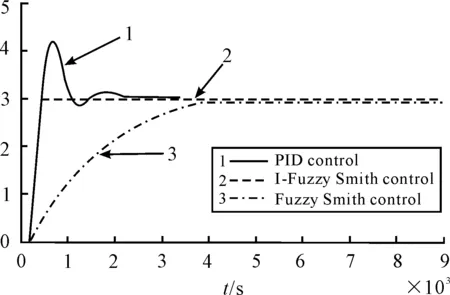
Figure 3.Response under different control method

5.1.Comparison of anti-jamming performance

The disturbance has very impact for control system[9]. The Figure 4 shows the control structure of simulation system under a disturbance. The system joins a step disturbance located in output of I-Fuzzy-Smith controller at timet=5 500 s, and the response curve is shown in Figure 5. The curve 1, curve 2, curve 3 is respectively the system response by PID, I-Fuzzy-Smith and Fuzzy-Smith control. From Figure 5 it can be seen that the I-Fuzzy-Smith control has better anti-jamming performance.

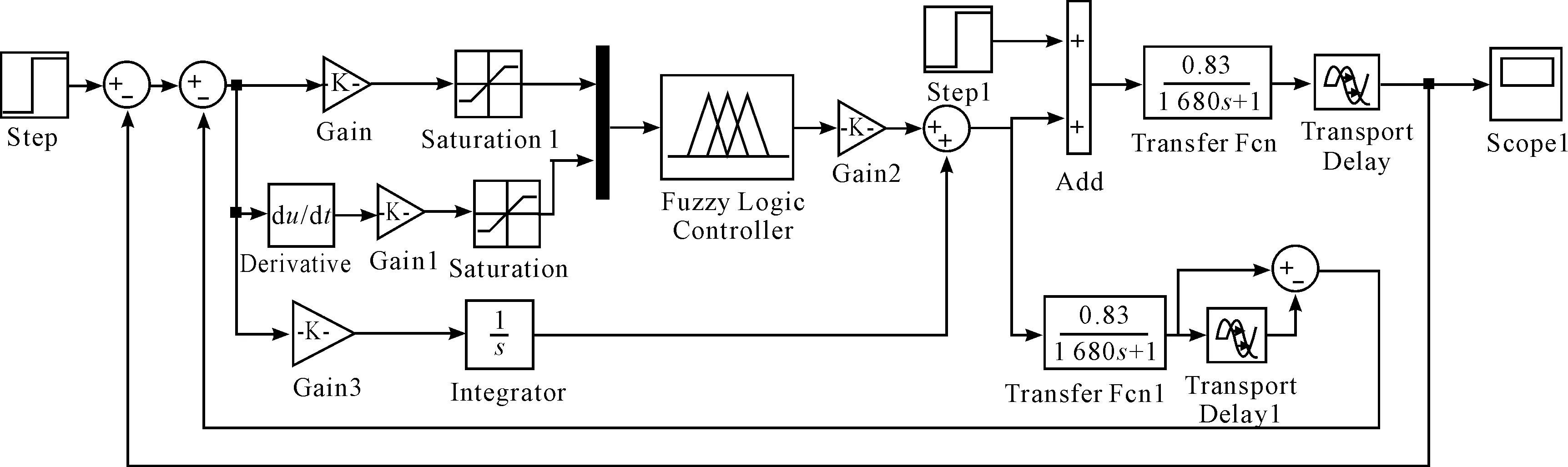
Figure 4.I-Fuzzy-Smith control structure with disturbance

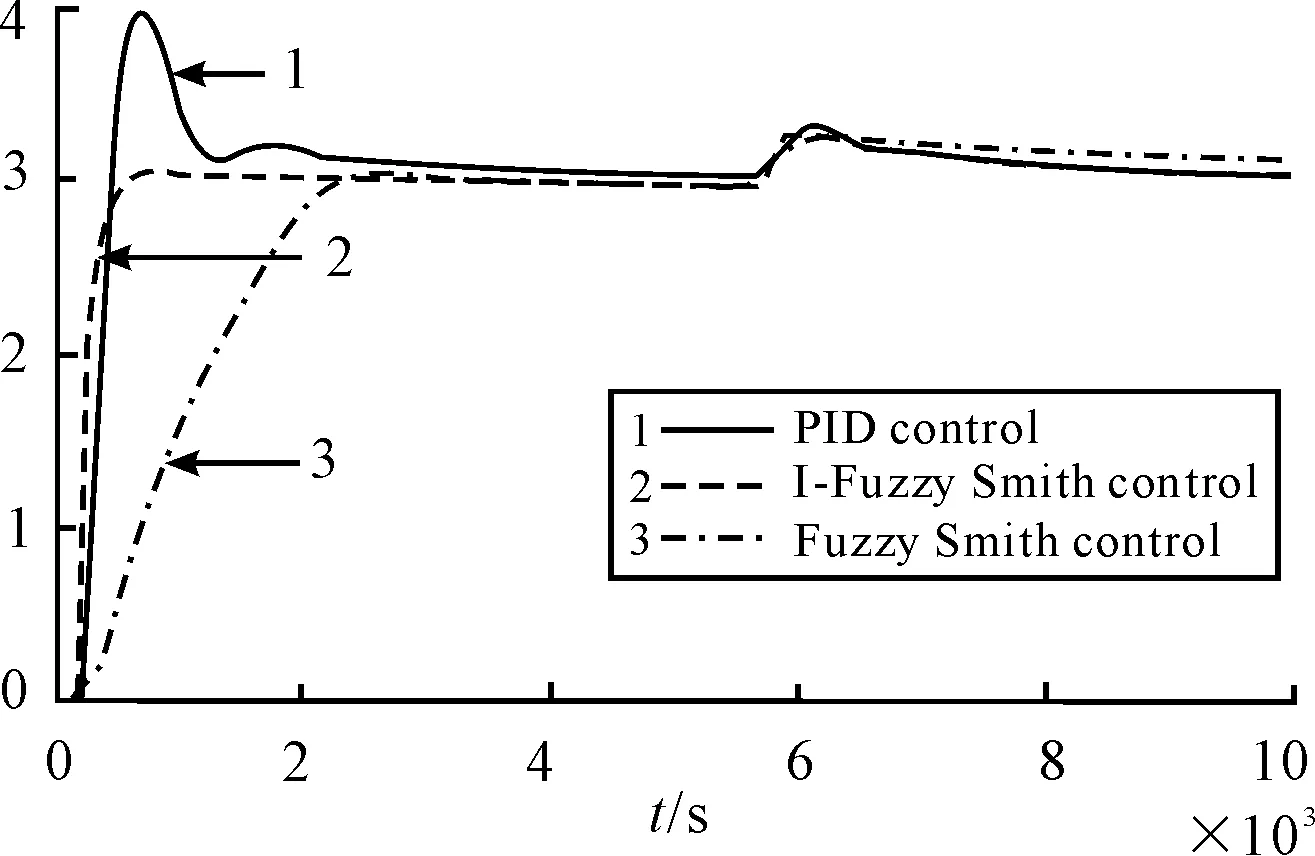
Figure 5.System response curve with disturbance

5.2.Robustness comparison for parameter change

1) Gain change

When the amplification coefficientKchanges from 0.83 to 3, the response of system is shown in Figure 6. The curve 1, curve 2 and curve 3 are respectively the system response by PID, I-Fuzzy-Smith and Fuzzy-Smith control. From Figure 6 it can be seen that the I-Fuzzy-Smith control has better anti-jamming performance. After gain changing, the overshoot of PID control is reduced from the original 40% to current 16.7%, and the steady-state error of Fuzzy-Smith control is reduced from the original 0.2 to current 0, and the rise time of I-Fuzzy-Smith control is reduced from the original 260 s to current 230 s.

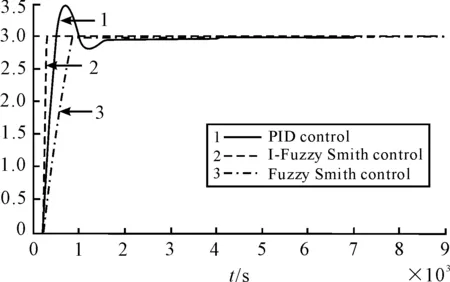
Figure 6.System response curve changed gain

2) Change for time constant

When the time constantTchanges from 1680 s to 1880 s the response curve is shown in Figure 7. The curve 1, curve 2 and curve 3 is respectively the system response by PID, I-Fuzzy-Smith and Fuzzy-Smith control. From Figure 7 it can be seen that the overshoot of PID control is reduced from original 40% to current 33%, the rise time of Fuzzy-Smith control is increased from the original 3 600 s to current 6 000 s, and the response of I-Fuzzy-Smith control is hardly any change. And therefore the robustness of I-Fuzzy-Smith control is better.

3) Change for pure time lag

When the pure time lag changes from 200 s to 400 s, the response is shown in Figure 8. The curve 1, curve 2 and curve 3 are respectively the system response by PID, I-Fuzzy-Smith and Fuzzy-Smith control. It can be seen that the overshoot of PID control is reduced from the original 40% to current 13%, and the PID control has 0.25 steady-state error, and the response curve of other control algorithms is hardly any change and only postpones the time 200 s.

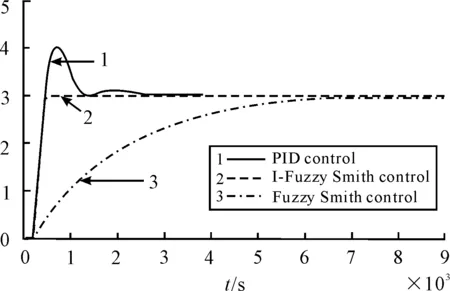
Figure 7.Response curve changed time constant

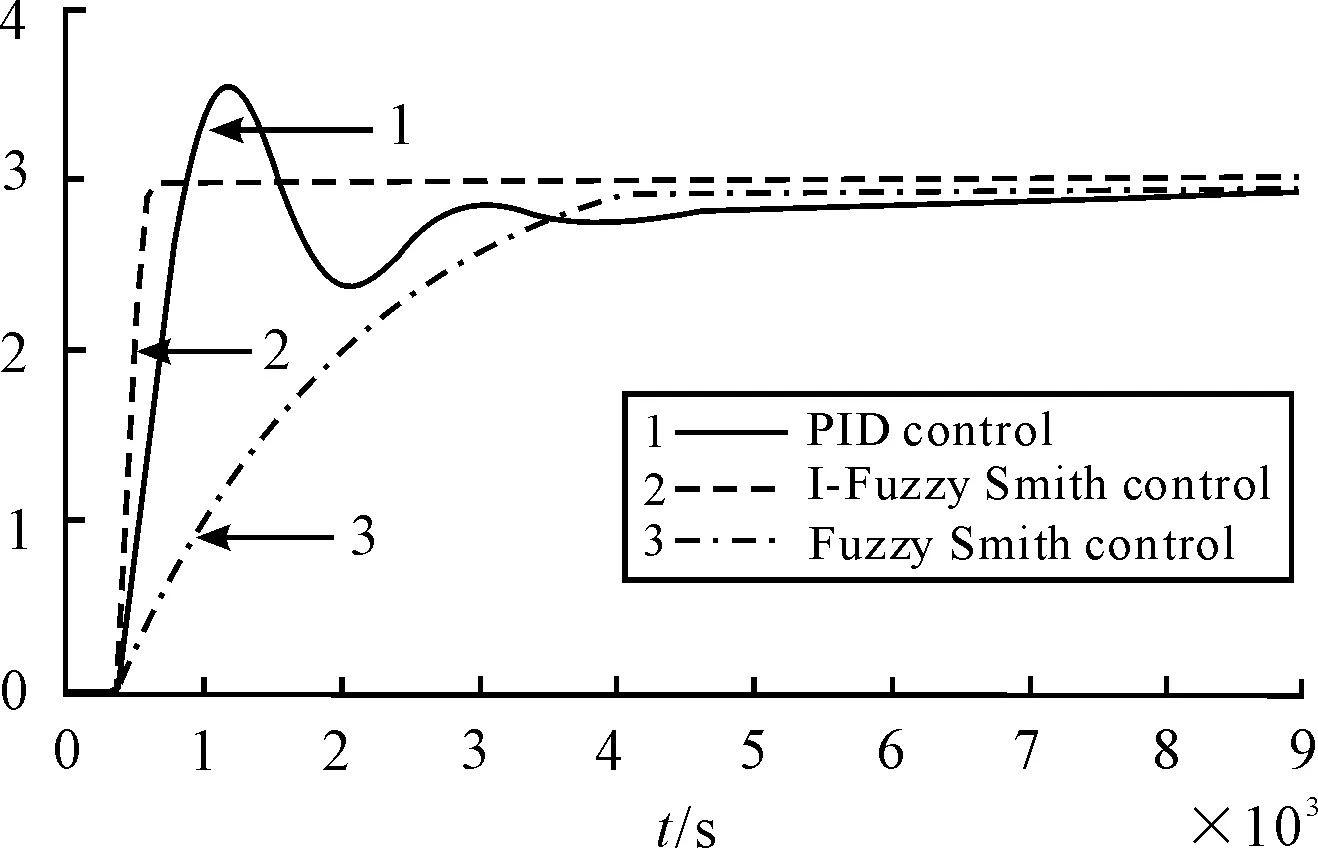
Figure 8.Response curve changed time lag

4) Add an inertia node in the original object

After an inertia node 1/(10s+1)is joined into the original object, the response curve is shown as in Figure 9. The curve 1, curve 2 and curve 3 are respectively the system response by PID, I-Fuzzy-Smith and Fuzzy-Smith control. It can be seen that the overshoot of PID control is increased from the original 40% to current 46.7%, the rise time of Fuzzy-Smith control is increased from the original 3600 s to current 6 000 s, but the I-Fuzzy-Smith control only appeared a 3.3% overshoot.

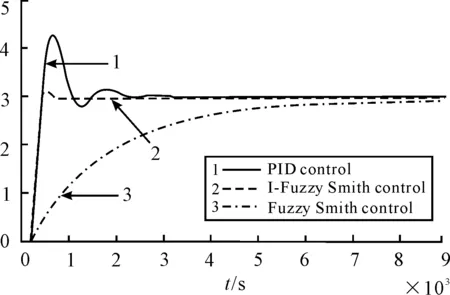
Figure 9　Response curve of 2-order system

5) Analysis of simulation

When the system is disturbed the control of I-Fuzzy-Smith has better anti-jamming performance than Fuzzy-Smith control and PID control. When the controlled object parameters change the control of I-Fuzzy-Smith has strong robustness performance than Fuzzy-Smith control and PID control, and it would be discussed as the following.

① After the gain gets large, all the rise and adjusting time of three methods are shortened, the response curve of Fuzzy-Smith control is no steady-state error, and the overshoot of PID control is reduced.

② After the time constant gets large, the response curve of I-Fuzzy-Smith control is hardly changed, the overshoot of PID control is reduced, and the rise time of response curve is increased for Fuzzy-Smith control.

③ After the pure time lag gets large, the response curve of I-Fuzzy-Smith and Fuzzy-Smith control is hardly changed, and it only the time is postponed to be 200 s. The overshoot of response curve is reduced for PID control, and it appeared the larger steady-state error.

④ After the inertia node is joined into the original controlled object, the response curve of I-Fuzzy-Smith control only appeared a smaller overshoot, and the rise time is increased for the response curve of Fuzzy-Smith control and appeared a small overshoot. The overshoot of response curve gets large for PID control.

6.Conclusion

Aiming at the uncertainty complex process with large pure time lag, the above discussed a sort of fusion control strategy based on I-Fuzzy-Smith algorithm. By means of Simulink toolbox, under the condition of MATLAB environment, the simulation shows that the proposed control method has stronger adaptive ability and robustness, and it owns better control effect for complex system with large pure time lag.

References

[1]WANG Yao-nan, SUN Wei. Intelligent Control Theory and Applications[M]. Beijing: China Machine Press, 2008.

[2]SUN Xiao-fang, CAI Yi-jun, PAN Hai-tian, et al. Research on self-adaptive intelligent fuzzy-Smith control for processes with large time-delay[J]. Industrial Instruments and Automation Equipment, 2008(5):6-9.

[3]LI Xiao-peng, LIU Jian-du. Smith’s algorithm based on fuzzy PID controller design[J]. Microcomputer Information, 2009, 25(11):66-67.

[4]HUANG Xiao-yin. Study on divided time period control for Temperature and humidity[J]. Automatic control and measurement, 2003(4):34.

[5]Bequette B W, Babatunde A. Ogunnaike. Chemical Process Control Education and Practice[J]. System Theory, 2005(3): 234-238.

[6]ZHANG Wei. Design and Research on Intelligent Control System of Temperature and Humidity in Pharmaceutical Workshop[D]. Changsha: Central South University, 2008.

[7]SHI Xin-min, HAO Zheng-qing. Fuzzy Control and its MATLAB Simulation[M]. Beijing: Tsinghua University press, 2008.

[8]ZHANG De-feng. MATLAB Fuzzy System Design[M]. Beijing: National Defense Industrial Press, 2009.

[9]PENG Li, LIN Ying, YANG Yi.Exploring on Related Technique in the Control of Complicated System[J]. Journal of Southwest China Normal University ( Natural Science Edition，2004, 29(6): 1066-1068.

一种不确定性复杂大时滞过程的融合控制策略*

毕波†

重庆交通大学 国际学院，重庆400074

摘要：针对不确定性导致的复杂大时滞过程控制精度低的问题，提出了一种基于算法融合的控制策略。研究了控制难点与控制论特性，基于大时滞复杂过程特性，融合了积分控制有利于消除稳态误差，Smith预估控制有利于时滞的补偿，模糊控制有利于处理某些不确定性控制，集成各自的优势，给出了一种I-Fuzzy-Smith控制算法。基于Matlab仿真，以大时滞惯性过程为例，分别采用PID、Fuzzy-Smith和I-Fuzzy-Smith控制进行了比较研究，响应验证了融合控制策略在系统动、静态性能和鲁棒性方面的优势。研究结果表明:提出的融合控制策略控制精度高，并表现出很强的鲁棒性。

关键词：模糊控制；Smith预估控制；积分控制；融合控制策略

中图分类号：TP273

DOI:10.3969/j.issn.1001-3881.2014.06.008

Received: 2013-11-20

*Supported by project of Chongqing Education Commission (2010-22-09)

† Bo BI, Associate professor. E-mail：804805129@qq.com