基于扩展卡尔曼滤波的磁悬浮轴承刚度阻尼辨识
,
(南京航空航天大学机电学院,江苏 南京210016)
基于扩展卡尔曼滤波的磁悬浮轴承刚度阻尼辨识
邹玥,周瑾
(南京航空航天大学机电学院,江苏 南京210016)
提出一种磁悬浮轴承刚度阻尼的测量方法,通过对转子施加不平衡质量激励,利用扩展卡尔曼滤波算法识别出磁悬浮轴承的刚度和阻尼。仿真研究表明,此方法可有效测量磁悬浮轴承刚度阻尼。经过试验辨识出使用的磁悬浮试验台的支承参数,并将辨识结果带回到仿真文件中进行验证对比,结果表明,可有效辨识出磁悬浮轴承的刚度阻尼参数。
扩展卡尔曼滤波;刚度;阻尼
0 引言
磁悬浮轴承的刚度和阻尼系数影响着控制系统参数优化、临界转速预估和不平衡响应计算等。因此,磁悬浮轴承的刚度和阻尼系数的辨识非常重要。针对五自由度、高速运转情况的下磁悬浮轴承刚度、阻尼测试与辨识还需完善。采用扩展卡尔曼滤波方法辨识磁悬浮轴承的刚度阻尼,使用不平衡量产生的简谐力作为激振力,基于有限元模型的仿真和实验,对磁悬浮轴承的支承参数进行辨识。
1 扩展卡尔曼滤波算法基本理论
磁悬浮轴承-转子系统试验台如图1所示。l1,l2为左右两侧磁悬浮轴承分别离转子质心的距离;d1,d2为左右不平衡质量分别离质心的距离;m1,m2分别为添加在左右两边圆盘上的不平衡质量大小;r1,r2为不平衡质量施加在2个圆盘的半径;p1,p2为位移传感器距转子质心的距离;用弹簧阻尼系统模拟磁悬浮轴承的支承情况。
对于磁悬浮轴承转子系统,考虑运动方程为:
(1)
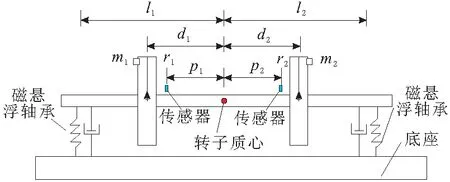
图1 磁悬浮轴承-转子系统试验台

图2 转子不平衡质量在转子施加位置
z为转子的振动位移信号,z={zx1,zy1,zx2,zy2}T,因耦合参数对系统影响较小,且为了计算的简化,忽略耦合参数,则刚度阻尼矩阵为:
(2)
(3)
kxxi,cxxi(i=1,2)为径向轴承X方向的刚度阻尼;kyyi,cyyi(i=1,2)为径向轴承Y方向的刚度。
转子受不平衡质量激励如图2所示,与参考轴夹角分别为φ1和φ2的位置,则运动方程右侧的F0可表示为:
(4)
ω为转子旋转频率;Ω为转子旋转角速度,Ω=2πω;转子轴承处的位移为zxi,zyi(i=1,2)。
在系统与控制理论中,常常用状态变量的形式来描述一个系统的运动。因此,可以用它来描述转子系统的运动。扩展卡尔曼滤波算法是非线性状态滤波的递推算法,可以将系统的状态和未知参数同时辨识出来[1-3],需将轴承参数作为状态变量的一部分。在扩展卡尔曼滤波算法中就是把转子的支承参数也看作状态向量,对于时不变的系统,该向量就是一个常数向量。将其与系统的真实状态向量s组合,构成增广状态变量,然后利用扩展卡尔曼滤波器对这个增广状态进行最优或者次优估计[4]。那么,可以设全局状态变量为:
(5)
r={kxx1,kyy1,kxx2,kyy2,cxx1,cyy1,cxx2,cyy2}T。
由于刚度阻尼参数未知,可将它们看成系统的另外8个状态,这样全部16个状态如下:
si为第i个自由度相对于基础的位移;
si+4为第i个自由度相对于基础的速度;
si+8为第i个自由度刚度系数
si+12为第i个自由度阻尼系数
i=1,2,3,4,系统的一阶微分方程组为:
=f(s,F,t)+w
(6)
f(s,F,t)中不为0的元素可以通过运动方程(1)转化得到。 由位移传感器测得并转换至磁悬浮轴承处的位移向量,即系统的输出量为Yk,Yk向量中也包含了测量误差,那么Yk与位移的实际值szk之间存在一个线性关系,即
Yk=Hszk+vk
(7)
Yk中的变量与各轴承处的位移有以下关系,则有观测方程为:
(8)
状态方程和观测方程都用离散时间的形式为:
s(k+1)=f[s(k),F0,t]·τ+s(k)+w
(9)
Y(k)=h[s(k),F0,t]+v(k)
(10)
s(k)为16维状态向量;Y(k)为4维轴承处位移;w(k),v(k)为零均值的正态白噪声序列;w(k)表示系统的描述误差;v(k)是测量中的噪声[5]。

预测阶段为[6]:
u(tk),tk]·τ
(11)

(12)
增益阵的计算为:

(13)
滤波阶段为:

(14)
P(tk+1|tk+1)=(I-Kk+1Hk+1)·P(tk+1|tk)
(15)
τ为采样时间间隔;Φ为转移矩阵。
(16)
Hk+1=H
(17)
(18)
(19)
估计准则是使状态向量的误差方差最小[7]。根据式(11)~式(19),只要给出系统参数及状态初始值的估计及初始误差的协方差阵,就可以对量测数据进行递推处理和计算。实际表明,对初始值的要求是非常低的,只要给出大约的量级就可以。这对实际应用是十分有利的,采用全局迭代的离线递推辨识算法,可以在有限数据量测的条件下能得到较高的参数估计精度,将预测阶段与滤波阶段反复进行后,状态变量中的支承参数会逐渐逼近真实值。
2 磁悬浮轴承刚度和阻尼的仿真研究
建立试验所用磁悬浮轴承-转子系统有限元模型,附加不平衡质量,计算出磁悬浮轴承处的位移响应。根据上述理论,可辨识出磁悬浮轴承的刚度和阻尼系数。有限元仿真时,先假定左侧磁悬浮轴承的刚度阻尼系数分别为:
K1=5×106N/m,C1=5 000N·s/m
右侧磁悬浮轴承的刚度阻尼系数分别为:
K2=6×106N/m,C2=6 000N·s/m
辨识出磁悬浮轴承的刚度和阻尼系数随旋转频率变化的曲线如图3和图4所示。

图3 20~200Hz刚度变化仿真值曲线
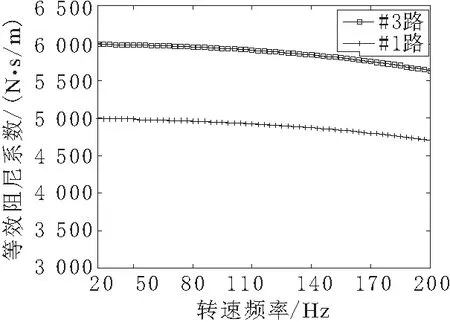
图4 20~200Hz阻尼变化仿真值曲线
由图可见参数识别精度较高,辨识结果在200Hz以内与原值误差较低,与初始给定值极为相符,辨识结果较为可靠。随着转速的升高,辨识值与真实值之间的误差也越来越大,主要考虑为随着转子转速的升高,转子的柔性逐渐显现出来,采用的动力学方程不能完全表达其运动规律。但在辨识范围内,即20~200Hz之间,仿真计算的误差基本处于10%以下,辨识结果较为可靠,该辨识方法用于辨识磁悬浮轴承的刚度阻尼参数具有一定的可行性。
3 磁悬浮轴承刚度和阻尼的实验研究
与仿真的算法相同,得到两侧磁悬浮轴承处的位移后,带入编制好的Matlab程序进行计算。对磁悬浮轴承的径向刚度阻尼值进行求解。各路方向各转速下磁悬浮轴承的刚度与阻尼曲线如图5所示。磁悬浮轴承在转子频率较低时刚度相对较小,随着转速的增加,刚度逐渐上升,阻尼在低速时也相对较小,随着转速的增加,阻尼逐渐上升。
将辨识所得的参数记录成txt文件,用Matlab编制好的程序将其中的辨识出的磁悬浮轴承的刚度阻尼系数,代入上一节的仿真文件中,替换掉其中转子的支承参数,计算对应不同频率,磁悬浮轴承处转子的位移响应,最后将此位移响应与实验采集的位移响应进行对比,以验证辨识结果的可靠性,EKF方法辨识效果验证如图6所示。
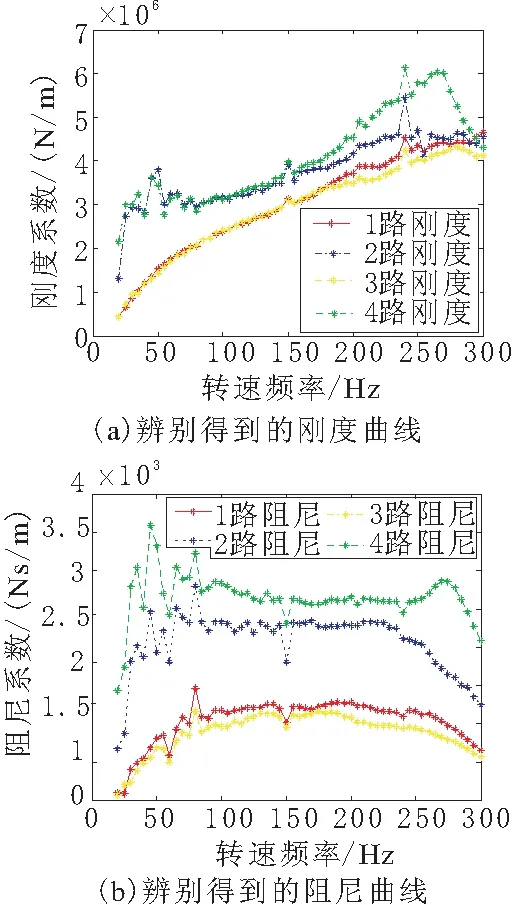
图5 各路方向各转速下磁悬浮轴承的刚度与阻尼系数
由验证结果图来看,在200Hz以下,将辨识出的数值反带回仿真文件中的计算出的幅值,与试验值基本吻合,相差较小,辨识结果可信。而200Hz转速以上,两者差值比较大,并在260Hz左右达到最大,说明在200Hz以上的辨识结果误差逐渐增大,辨识结果可靠程度降低。所以,在200Hz以下的范围,辨识结果相对可靠。

图6 EKF方法辨识效果验证
4 结束语
提出了一种磁悬浮轴承刚度和阻尼系数的测试方法。进行了不平衡质量试验仿真,根据扩展卡尔曼滤波算法建立迭代方程,对磁悬浮转子系统支撑参数进行了辨识。对比设定值表明,识别方法对磁悬浮轴承参数辨识的有效性。并进行不平衡响应实验,对磁悬浮转子实验台进行辨识支承参数,辨识结果带回仿真文件的结果表明,辨识结果比较可靠。
[1] Brad A.Miller,Samuel A.Howard.Identifying bearing rotor-dynamic coefficients using an extended Kalman filter[J].Tribology Transactions,2009,52(5):671-679.
[2] 宝志雯,史文月.基于推广卡尔曼滤波算法的结构模型的参数识别[J].振动与冲击,1990(1):11-21.
[3] 童余德,周永余,陈永冰,周岗. 基于Matlab的卡尔曼滤波法参数辨识与仿真[J].船电技术,2009(8):47-50.
[4] 樊素英,李忠献.基于广义卡尔曼滤波的桥梁结构物理参数识别[J].计算力学学报,2007(4):472-476.
[5] 吴子燕,丁兰,刘书奎.基于广义卡尔曼滤波的桥梁结构物理参数识别的子结构法[J].西北工业大学学报,2010(3):425-428.
[6] Gelb A.Applied Optimal Estimation.Cambridge:MIT Press, 1974.
[7] 仲卫进,艾芊.扩展卡尔曼滤波在动态负荷参数辨识中应用[J].电力自动化设备,2007(2):47-50.
Identification of the Magnetic Bearings Support Parameters Using an Extend Kalman Filter
ZOUYue,ZHOUJin
(College of Mechanical and Electrical Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
An identify measurement of stiffness and damping to AMB system is introduced.By applying unbalance excitation to the rotor,stiffness and damping can be identified use extended Kalman filter(EKF) algorithm.The simulation result shows that it is efficient for this method to measure the stiffness and damping of AMB.Then used the method to identify the supporting parameters in experiment and brought the identified results to simulate files to compare the displacement response.The results indicated that the EKF method can efficiently identify the stiffness and damping.
extend Kalman filter;stiffness;damping;Magnetic bearing
2014-02-24
国家自然科学基金资助项目(51075200);江苏省自然科学基金资助项目(BK2011070)
TH999
A
1001-2257(2014)11-0012-04
邹玥(1989-),女,安徽芜湖人,硕士研究生,研究方向为磁悬浮轴承技术;周瑾(1972-),女,江苏徐州人,博士,教授,研究方向为磁悬浮技术、转子动力学和机电系统控制。

