基于非线性有限元的橡胶隔振器压缩刚度的研究
秦洪艳
(三江学院 机械工程学院,江苏 南京 210012)
基于非线性有限元的橡胶隔振器压缩刚度的研究
秦洪艳
(三江学院 机械工程学院,江苏 南京 210012)
借助ANSYS软件完成了压缩状态下矩形橡胶隔振器的非线性有限元分析,总结了矩形橡胶隔振器压缩刚度计算公式中形状系数的确定方法,并与传统经验公式进行了比较。
矩形橡胶隔振器;形状系数;非线性有限元
由于橡胶材料具有良好的弹性性能和缓冲功能,工程机械设计中通常采用橡胶隔振器达到支承、限位、隔振及减噪的目的。
为了方便设计计算,通常将复杂形状的橡胶隔振器看成是几个简单形体的叠加。国内外对典型形状的橡胶隔振器刚度计算方法进行了研究,一些机构也总结出计算典型橡胶隔振器刚度的经验公式。但橡胶属于典型的非线性弹性材料,其使用性能随橡胶配方、使用环境、隔振器造型及受力变形量而变化,因此传统的经验公式具有一定的局限性。
本文借助有限元分析软件ANSYS对压缩状态下的矩形橡胶隔振器进行非线性有限元分析,从而得到矩形橡胶隔振器压缩刚度计算公式中形状系数的表达式,此表达式同样适用于其他形状的橡胶隔振器。
1 矩形橡胶隔振器压缩刚度的计算
橡胶作为一种非线性弹性材料,其基本的物理性能不会由于外表形状的改变而改变,但制成隔振器后它的弹性模量不再是橡胶材料的弹性模量E,而是表观弹性模量Ea。表观弹性模量与弹性模量的关系为:
(1)
因此,橡胶隔振器压缩刚度Kx的计算公式为[1]:
(2)
式中:AL为橡胶块的约束面积;H为矩形橡胶块的高度;m为形状系数,其大小与橡胶隔振器的约束面积AL与自由面积AF的比值n有关,如图1所示。形状系数的表达式为:
(3)
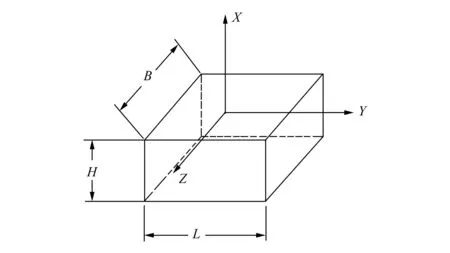
图1 矩形橡胶块
对于矩形橡胶隔振器来说
式中:L为矩形隔振器的长;B为矩形隔振器的宽。
只要确定了形状系数m=f(n)的表达式,橡胶隔振器的压缩刚度可以通过式(2)计算。而橡胶材料的形状、硬度、变形量都会对形状系数m产生影响。
上海橡胶研究所总结的形状系数经验公式是:
(4)
日本机械学会总结的形状系数经验公式是:
(5)
(6)
(7)
2 利用有限元法计算矩形橡胶隔振器的形状系数
对标准橡胶试样进行单轴拉伸和压缩试验,可以得到该橡胶材料的应力-应变曲线,图2是邵氏硬度HA=65时的橡胶试样的平均应力-应变曲线,该曲线用于计算隔振器的弹性模量E,以及确定橡胶材料的Mooney-Rivlin常数。
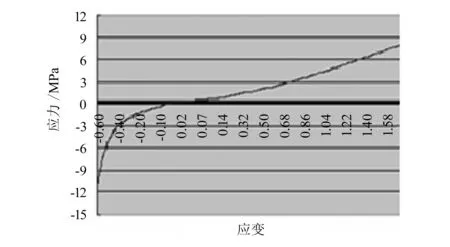
图2 HA=65的橡胶试样的平均应力-应变曲线
借助ANSYS软件对压缩状态下的矩形橡胶隔振器进行非线性有限元分析,可得到某一压缩量下的载荷-位移关系,具体步骤如下:
a.在ANSYS软件中建立矩形橡胶隔振器的有限元模型,包括定义单元类型、创建节点和单元,同时定义材料性质等。
b.输入对橡胶材料标准试样的实测实验数据,通过橡胶材料的应力-应变曲线确定Mooney-Rivlin常数的个数,如果橡胶材料的应力应变曲线没有拐点(反弯点),则Mooney-Rivlin常数为2个;有1个拐点,Mooney-Rivlin常数为5个;有2个拐点,Mooney-Rivlin常数为9个。图2所示的应力-应变曲线只有1个拐点,因此Mooney-Rivlin常数为5个,借助ANSYS软件计算Mooney-Rivlin常数[2]。
c.对矩形橡胶隔振器进行加载,设置载荷步和各项参数。
d.求解并进行结果的后处理。
图3为ANSYS后处理器中显示的矩形橡胶隔振器压缩量为10%时的变形情况。通过时间历程后处理器定义了隔振器顶面位移和顶面承受载荷2个变量,得到图4所示的载荷-位移关系曲线。
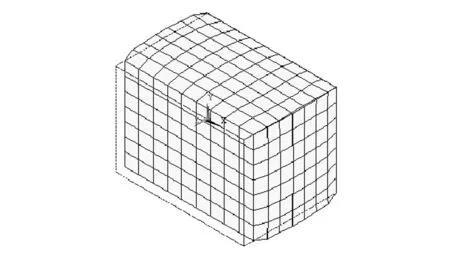
图3 压缩量在10%的矩形橡胶隔振器的变形情况
通过载荷-位移曲线可以求橡胶隔振器的表观弹性模量Ea,该压缩量下,橡胶材料的弹性模量E可以通过拉伸压缩试验得到的应力-应变曲线进行求解,并利用公式(1)求解压缩刚度的形状系数m。改变隔振器的外形尺寸,可以得到若干组m=f(n)的对应关系。
橡胶隔振器用于减振设计时,通常压缩变形量控制在15%以下。分别计算压缩量为5%,10%,12%和15%时橡胶隔振器的刚度特性,得到了HA=65时的矩形橡胶隔振器在不同压缩量下的表观弹性模量Ea,见表1。

表1 HA=65时橡胶材料在不同压缩量下的表观弹性模量Ea
遵循前述方法与步骤得到多组m-n的对应关系。借助ORIGIN或MATLAB软件,利用最小二乘法求解形状系数表达式m=a+bn+cn2,得到不同压缩量下的m-n关系,见表2。

表2 HA=65时矩形橡胶隔振器在不同压缩量时的m-n对应关系
将非线性有限元法获得的矩形橡胶隔振器在不同压缩量下形状系数的表达式与经验公式(4)和经验公式(5)的计算结果进行比较,结果如图5所示,横坐标为n,纵坐标为形状系数m。很明显,由日本机械协会的经验公式(5)计算的形状系数m的值误差较大,不适合此隔振器;当0.2 图5 非线性有限元法得到的形状系数同传统经验公式计算结果的比较 橡胶隔振器的使用性能受橡胶的配方、硬度、温度以及隔振器的外形尺寸、施加载荷、变形量等许多因素影响[3]。传统橡胶隔振器压缩刚度的形状系数是通过对类似模型进行试验得到,然后再进行产品试验,纠正设计计算的误差,这种方法得到的经验公式不仅误差大,而且浪费大量的人力物力。 目前ANSYS、ADINA、ABAQUS等有限元软件已具备橡胶超弹性特性材料和体积近似不可压缩材料的大变形有限元计算功能,借助这些专用软件可以实现橡胶隔振器的有限元仿真设计。应用有限元软件对橡胶隔振器进行静态和动态特性分析,不仅可以得到较为精确的压缩刚度,而且可以实现产品的优化设计,既提高了隔振器的设计质量,又减少了试验次数,节约了试验耗材。 [1] 严济宽.机械振动隔离技术[M].上海:上海科学技术文献出版社,1985:277-290. [2] 王利荣,吕振华.橡胶隔振器有限元建模技术及静态弹性特性分析[J].汽车工程,2002(6):480-485. [3] 秦洪艳,张红.圆柱形橡胶垫刚度经验公式的研究[J].青岛农业大学学报,2007(3):59-61. Researchoncompressionstiffnessofrubberisolatorbasedonnonlinearfiniteelement QIN Hongyan (Sanjiang University, Jiangsu Nanjing, 210012, China) It introduces the nonlinear finite element analysis used to the compressed rectangular rubber isolator with the help of ANSYS software, describes the computing method of the shape factor of compression stiffness. It compares the results with the traditional empirical formula. rectangular rubber isolator; shape factor; nonlinear finite element 10.3969/j.issn.2095-509X.2014.11.016 2014-10-20 秦洪艳(1981—),女,山东潍坊人,三江学院讲师,硕士,主要从事车辆振动方面的研究。 TB535 A 2095-509X(2014)11-0074-03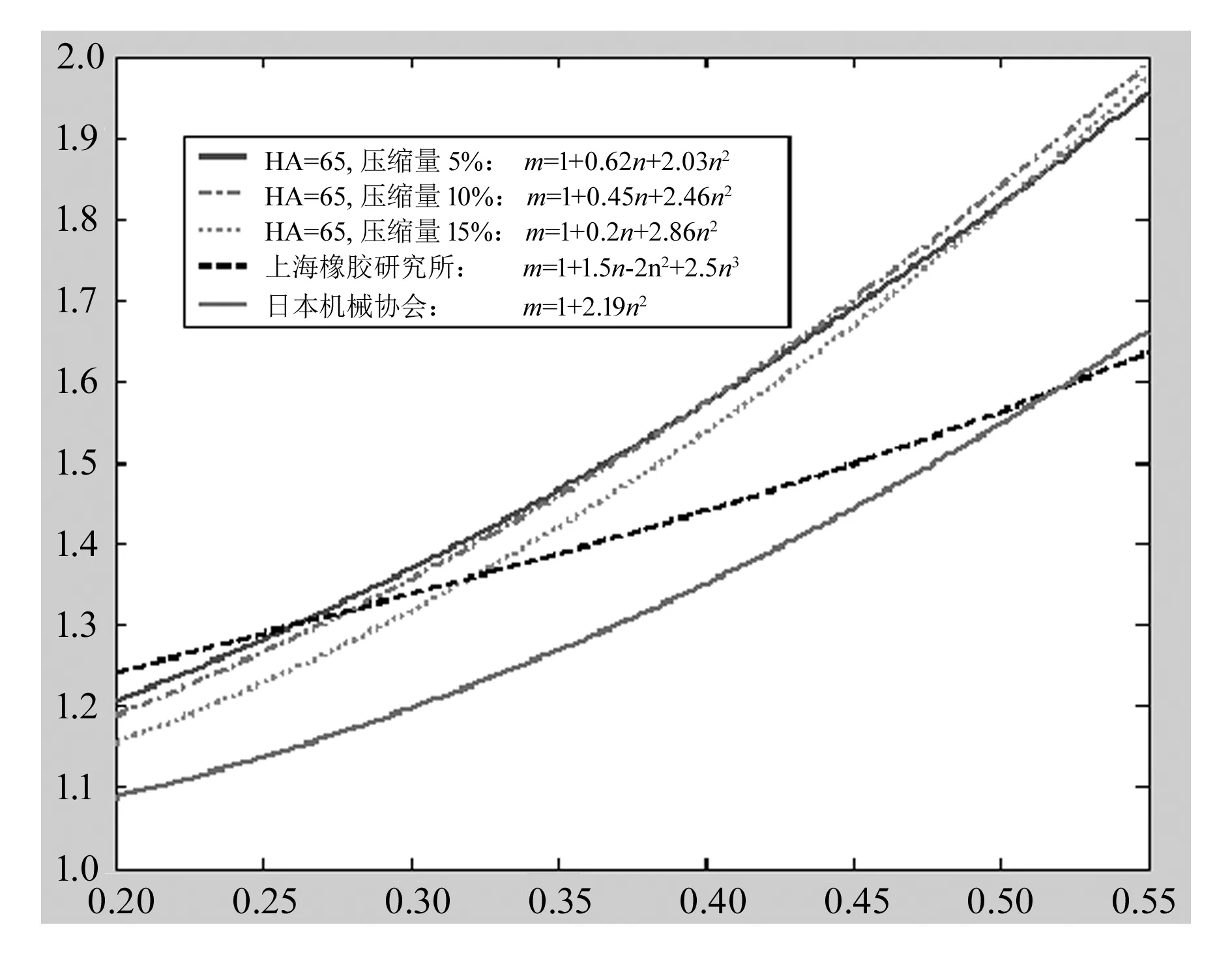
3 结束语

