啄木鸟装置自激振动的动态仿真

许 勇，王 伟

(上海工程技术大学 机械工程学院，上海 201620)

啄木鸟装置自激振动的动态仿真

许 勇，王 伟

(上海工程技术大学 机械工程学院，上海 201620)

啄木鸟装置可以产生自激振动，这种运动需要依赖摩擦力的作用,从而完成一系列的动作。为了研究啄木鸟装置系统的非线性的复杂运动过程，通过拉格朗日方程对自激振动中线性互补问题进行求解，从而得到啄木鸟装置的运动特性。啄木鸟装置可以通过自身的自激振动，而不需要依赖任何的动力和控制完成周期性的运动。整个连续周期的动态仿真表明其是稳定的周期被动运动，试验样机也验证了仿真的正确性。

被动运动；自激振动；动态仿真

为解决单侧接触的线性互补问题，近几十年来单侧接触的线性互补模型的公式广受关注[1]，然而在过去的10年里，这个公式才在数学和物理领域得到验证。在20世纪70年代和80年代Vereshchagin、Armstrong and Green[2-3]最早做了一些关于单侧接触的线性互补问题的研究。 LÖtstedt[4]发表了第一篇有关单侧接触的线性互补问题的文章。

所谓自激振动，就是无外界刺激，单纯靠振动系统本身的运动向整个系统提供动能。自激振动也叫负阻尼振动，这是由于整个系统的阻尼力非但没有阻止运动，反而维持系统的振动[5]。

啄木鸟装置的自激振动也是单侧接触线性互补问题的一种，啄木鸟模型通过弹簧连接在套筒上，将套筒置于金属直杆的顶端，拉开啄木鸟，放手后啄木鸟开始有节奏地摆动身体，一边啄杆一边间歇地、时滑时停地向下滑动，演示了自激振动的现象，也可作为多体系统动力学的教具。本文以啄木鸟装置模型为例，从实验、理论和模拟仿真上对这个问题进行求解分析[6]。

1 模型的建立

图1的啄木鸟装置由于冲击和摩擦的作用完成了一系列的动态行为。整个啄木鸟系统由啄木鸟1、套筒2、直杆3、弹簧约束组成。在啄木鸟的整个运动过程中，维持运动的能源来自重力[7]。套筒2往下滑动时，重力势能转换成维持啄木鸟运动的动能。而套筒与直杆之间的碰撞使得向下滑的动能转换成了啄木鸟往复摆动的动能和弹簧的势能。啄木鸟自身的重力势能并不是周期变化的，但是它对啄木鸟运动的输送是周期变化的，这是由于啄木鸟自身可以控制重力势能的能量分配，啄木鸟整个运动过程如图2所示[8]。

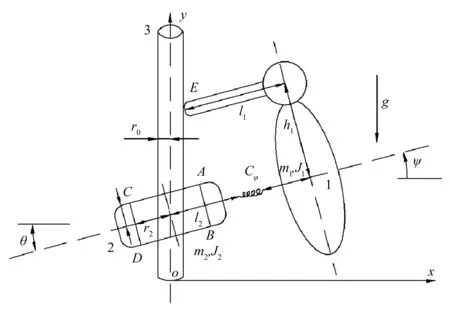
图1 啄木鸟装置 图中变量参数改为斜体

为了方便分析整个啄木鸟的运动过程，将啄木鸟1与套筒2组成的系统记作{0}，质量和为m。1与2由一根弹簧连接，弹簧为扭簧，仅产生由角位移引起的扭矩，本系统由3个自由度组成，q=[yθψ]，各参数的含义如图1所示。由于啄木鸟的运动需要依靠碰撞的干扰作用，所以本系统只有在摩擦力存在的情况下才可以运动[9]。

图2 啄木鸟运动过程示意图

在振动理论中，这种由本身的控制阀从恒定能源吸取能量而实现的不衰运动称为自激振动。这种由库仑摩擦激发的干摩擦自激振动是工程技术中常见的振动形式[10]。

在多体系统动力学中，对线性互补问题有一个整体的动力学方程描述，表示为

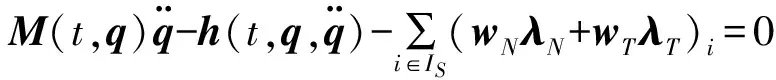
(1)

式中：M表示广义质量矩阵；t表示啄木鸟自由下落的时间;q表示广义坐标矩阵；h表示广义力；λN和λT分别表示法向以及切向的接触力；时间变量集合IS涵盖了所有潜在的约束。

由多体系统动力学的知识可以列出相关的矩阵

式(1)中，wN，wT是根据物体的几何形状特征以及物体间碰撞的动能原理计算出来的,分别为

啄木鸟被释放后，基于自激振动机理的动力学方程为：

(2)

(3)

(4)

式中：m2为套筒的质量；J2为套筒的转动惯量；m1为啄木鸟的质量；J1为啄木鸟的转动惯量；其他尺寸参量表示的含义如图1所示。式(2)、(3)、(4)分别表示整个系统{0}、套筒2、啄木鸟1的3个动力学方程。当不考虑外力时，可以很容易地解出这一方程组，从而求出各时刻啄木鸟的状态[11]。

2 啄木鸟的动态仿真

本动态仿真具体参数设置如下。

2.1动力学参数

m1=4.8g，m2=1.0g，g=9.81m/s2，J2=5.0×10-9kg·m2，J1=7.0×10-7kg/m2，cφ=0.005 6N·m/rad。

2.2几何参数

r0=0.001 35m，h2=0.004 42m，r2=0.001 75m，h1=0.020 0m，l2=0.010 0m，l3=0.015 0m，l1=0.020 1m，r1=0.002 0m。

2.3接触点

套筒与杆：μ=0.3，ξN=0，ξT=0，ν=0。

杆与啄木鸟：μ=0.3，ξN=0.5，ξT=0，ν=0。

将上述参数带入拉格朗日方程，用仿真软件可得到各参数随时间变化的示意图，如图3所示，其中θ和ψ的运动曲线呈周期性变化。

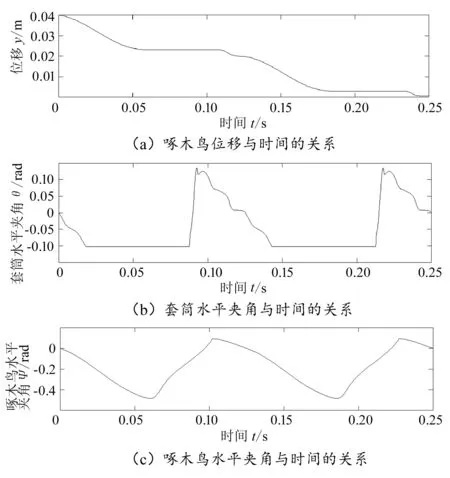
图3 各参数变化示意图

3 样机的运动

为了验证仿真结果的正确性，通过样机的制作，得到了图4所示啄木鸟装置的样机。其中，用一根粗的尼龙绳代替直杆，啄木鸟则是按照模型取适当比例剪裁得到，将啄木鸟套于绳上，从顶端自由下落，其运动恰好是周期性的被动运动。

样机运动示意图如图4所示。

4 结束语

本论文通过对线性互补问题的求解对啄木鸟装置系统的非线性动力学行为进行了研究。啄木鸟装置可以通过自激振动的原理，本身不加任何驱动和控制而实现周期性的运动。动态仿真的数据曲线很直接地显示了啄木鸟装置系统振动的周期性，这表明该装置能够实现周期性的、稳定的被动运动。

图4 样机运动示意图

[1] Pfeiffer F. The idea of complementarity in multi-body dynamics[J]. Archive of Applied Mechanics，2003，72(11/12)：807-816.

[2] Vereshchagin A F. Computer simulation of the dynamics of complicated mechanisms of robot manipulations[J].Eng. Cybern., 1974(6)：65-70.

[3] Armstrong W W,Green M W. The dynamics of articulated rigid bodies for purposes of animation[J]. Visual Computer,1985(1):231- 240.

[4] LÖtstedt P. Coulomb friction in two-dimensional rigid body systems[J]. Zeitschrift fur Angewandte Mathematik und Physik,1981，61(2)：605-615.

[5] 徐阳，卢毓江，秦剑生，等.测定悬臂梁固有频率[J].硅谷，2011(17)：174-175.

[6] Leine R I. Nonlinear dynamics and modeling of various wooden robots with impact and friction[J]. Journal of Vibration and Control，2003(9)：25-78.

[7] Slavic J，Boltezar M.Non-linearity and non-smoothness in multi-body dynamics: application to woodpecker toy[J]. Chinese Journal of Mechanical Engineering,2005，19(4)：491-496.

[8] Cline M B. Rigid body simulation with contact and constraints[D].City of Vancouver：The University of British Columbia，1999.

[9] 刘延柱.再谈荡秋千——兼谈自激振动[J].力学与实践，2007(3)：92-93.

[10] Baraff D. Dynamic simulations of non-penetrating rigid bodies[D]. New York：Cornell University，1992.

[11] 易舜智，晋晓曦，张晚云，等.以啄木鸟玩具为例的LCP问题求解[J].物理与工程，2013(5)：27-32.

Dynamicsimulationofawoodpeckerdevicebasedonself-excitedvibration

XU Yong, WANG Wei

(Shanghai University of Engineering Science, Shanghai, 201620, China)

Woodpecker device can generate self-excited vibration, and need to rely on the friction force to complete a series of actions. In order to study the complex nonlinear motion process of woodpecker system, it solves the linear complementary problem in self-excited vibration based on the Lagrange equation, and obtains the motion characteristics of the woodpecker device. The self-excited vibration woodpecker device can complete periodic motion, and does not need to rely on the power and control. Dynamic simulation of the whole continuous cycle show that the cycle motion is passive and stable, test prototype is also verified the correctness of the simulation.

passive movement; self-excited vibration; dynamic simulation

10.3969/j.issn.2095-509X.2014.11.011

2014-09-30

许勇(1973—)，男，江苏南通人，上海工程技术大学副教授，博士,主要研究方向为机器人机构学、机电装备动力学性能优化设计。

O323

A

2095-509X(2014)11-0051-04