A decision model of optimal production reliability and warranty length in an imperfect production system
Wu Junjian Wang Haiyan
(School of Economics and Management, Southeast University, Nanjing 211189, China)
A decision model of optimal production reliability and warranty length in an imperfect production system
Wu Junjian Wang Haiyan
(School of Economics and Management, Southeast University, Nanjing 211189, China)
A decision model to maximize the total profit of manufacturers in an imperfect production system is constructed. In this model, the production reliability and the warranty length are jointly used as decision variables for the case that products are sold with a warranty; i.e., the demand is dependent on the warranty length and sale price. Also, all the non-conforming quality (defective) items in the production process are refurbished to conform to quality ones at a cost. The existence and uniqueness of the optimal values of production reliability and the warranty length are proved by using the Euler-Lagrange method in analyzing the model. A numerical example is also provided to illustrate the effectiveness of the decision model. The sensitivity analysis of the key parameters of the optimal solution and objective value is presented in addition.
imperfect production system; warranty length; production reliability; Euler-Lagrange method
This paper intends to construct a decision model to maximize the total profit for manufacturers. To reach the goal of profit maximization, manufacturers need to increase the revenue and reduce the costs. To increase the revenue, product quality is an important factor for manufacturers to attract more buyers. Therefore, producers often provide a longer product warranty as a guarantee of the good quality of the products.
Some researchers studied the optimal production policy under the condition that products are sold with a warranty in an imperfect production system[1-4]. Other researchers focus their attention on the sale policy under the condition when products are sold with warranty. They presented a model to determine the optimal sale price and the warranty length with profit maximization[5-7]. However, one of the problems for these studies is that the rework cost of imperfect items is ignored.
On the cost control side, manufacturers need to reduce the defects. Ideally, the production system should work under perfect conditions and have zero defects by drawing maintenance policy for production machines[8]. In reality, however, the production system can have different problems for different reasons, such as machine aging, workers’ mistakes, etc.; i.e., the production system is imperfect[9]. Under these conditions, the production system will produce non-conforming quality (defective) items. The defective products are usually refurbished so that materials can be reused and the value of the defective items be recovered. Obviously, the manufacturers should minimize the rework cost.
The rate of defective items is related to the reliability of the production process. There are two different approaches for studying the reliability of production processes in the literature. The first approach proposes that the production system is required to produce 100% conforming quality items when appropriate advanced machineries and technologies are used. However, malfunctions of the production system do occur from time to time. The reliability of the production system is the rate of defects and the total products. This rate is denoted byθwhich is between 0 and 1, i.e.,0<θ≤1. Manufacturers will determine the optimal value ofθto maximize the profit or minimize the cost[10-11]. The second approach contends thatθis a number which is between a maximum value and a minimal value due to the production machines constraint and basic product quality required, i.e.,θ∈[θmin,θmax]. The production reliability is a decision variable which can be adjusted to the optimal value to maximize profit[12-14]. However, either of these two approaches considers the product warranty policy.
To remedy these problems, we try to develop a model by optimizing production reliability and warranty length simultaneously for an imperfect production with rework items.
1 Problem Description and Assumptions
All the manufacturers want to gain a competitive edge in the market and achieve a higher profit. So, in the production process, they must make an effective investment decision concerning the reliability of the production process; i.e., they need to determine the optimal production reliability. For the same type product, a higher reliability in the production process can help the firm to obtain more profit in a competitive market. At the product sales stage, the manufacturers need to make an effective sale policy. The product warranty policy is widely used as an incentive to attract more customers. Thus, the manufacturers need to determine an optimal product warranty length. Both the reliability of the production process and warranty length are related to the manufacturers’ profits. Therefore, the manufacturers need to determine the optimal reliability of the production process and optimal warranty length in order to maximize the total profits of the production system.
The decision model is built with the following assumptions:
1) The imperfect production system produces only two types of items for a single product, conforming quality items and nonconforming quality (defective) items. A defective item can be refurbished at the cost of making a conforming item.
2) The production rate is greater than the demand of the product; i.e., shortage is not allowed.
3) The failure rate of post-sale products follows an exponential failure distribution.
4) The length of the production cycleTis finite.
2 Formulation and Analysis of the Model
2.1 Formulation of the model
The total cost consists of the development cost, the unit production cost, rework cost for defective items, inventory holding cost and warranty cost. The effects of inflation and time value of money also should be considered.
The development cost is a function of product reliabilityθ. It can be expressed as[15]
DC(θ)=A+Bek(θmax-θ)/(θ-θmin)
(1)
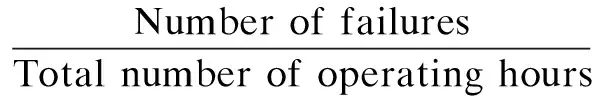
The unit production cost is a function of product reliabilityθand dynamic production ratep(t). It is expressed as[6]
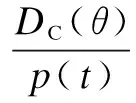
(2)
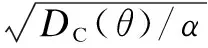
The demand function depends log-linearly on the sale priceSPand the warranty lengthW. It can be expressed as[7]
(3)
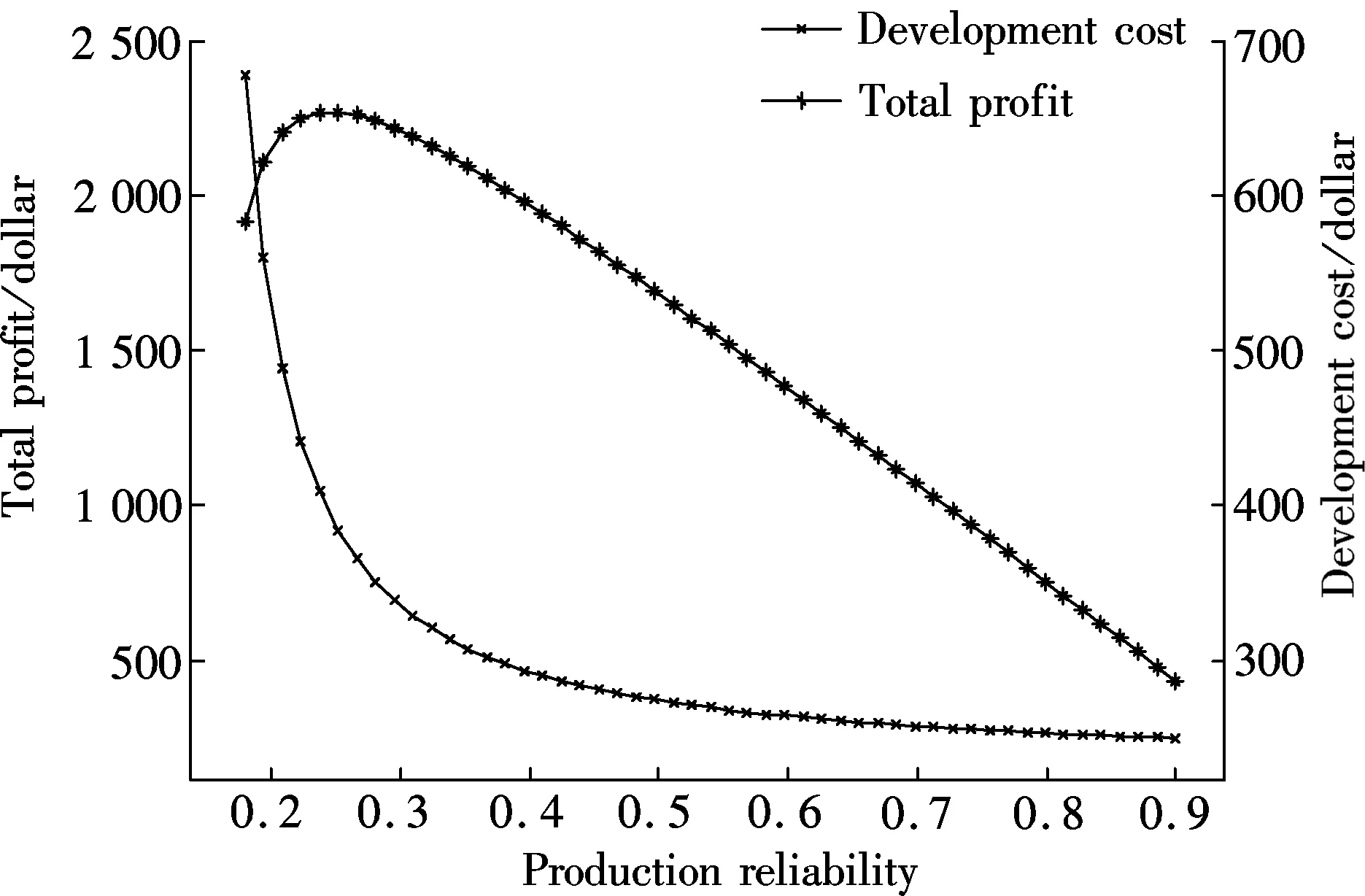
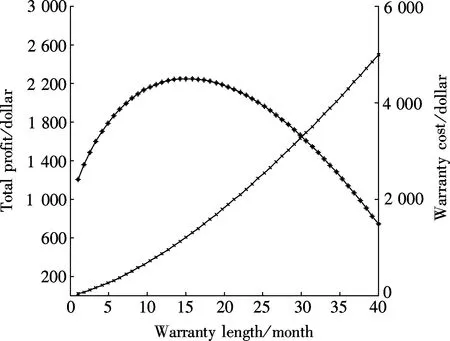
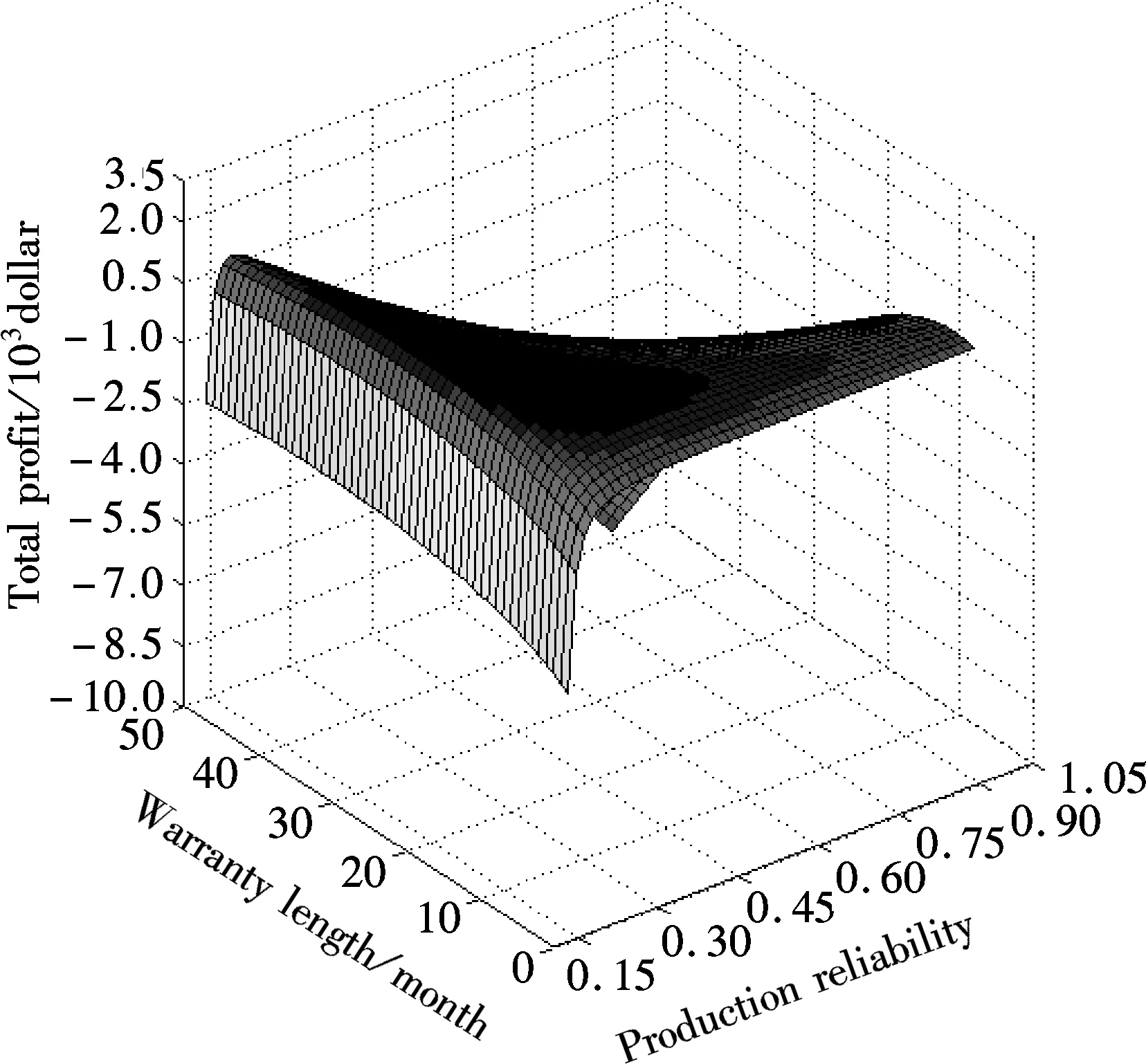
wherek1>0,k2≥0,a>1 and 0 In this paper, we assume that the product failure rate is exponentially distributed. When the production reliability is denoted byθand the repair cost per unit item is denoted byR2. It is easy to obtain the expected warranty cost during the warranty periodR2θWD. We assume that the on-hand inventoryQ(t) is zero att=0 andt=T, i.e.,Q(0)=Q(T)=0. The change of the inventory level can therefore be expressed as the following differential equation: (4) Inflation exists in every economy, especially, in developing economies and the inflation rate will in turn affect the interest rate. To incorporate the effects of the interest rate and the inflation rate, we userandito denote the interest rate and the inflation rate respectively, and thusδ=r-i. From the previous analysis, the total profit function with the effect of inflation and time-value of money during [0,T] can be expressed as (5) where (6) 2.2 Analysis of the model Lemma 1 The total profit functionπhas a maximum value withQ=Q(t) in the interval [0,T]. Proof We denote Qε(t)=Q(t)+εζ(t)t∈[0,T] (7) whereεis a sufficiently small variable;ζ(t) is a first continuous differentiable function oftandζ(t)≥0 for all values oft. FromQε(0)=Qε(T)=0, it is clear thatζ(0)=ζ(T)=0. The value of the total profit functionπforQε(t) is given by (8) (9) (10) (11) (12) Substituting Eq.(11) and Eq.(12) into Eq.(10), we obtain (13) Therefore, by the differential and integral calculus, we find that the profit functionπhas a maximum value. The proof is completed. The Euler-Lagrange equation for the maximum value ofπis (14) Substituting Eq.(6) into Eq.(14), we obtain (15) whereN=SP-MC0+w0θ>0 andw0=MC1-R1<0. Solving the second order differential equation, we obtain that the general solution ofQ(t) is (16) whereEandFare the abstract functions. Now, using the boundary conditions,Q(0)=0=Q(T), the values ofEandFare (17) Using Eq.(4), the optimal dynamic production rate is obtained as (18) Substituting Eq.(18) into Eq.(5), the total profit function can be expressed as (19) Proof Letπbe a function ofθ, i.e.π=π(θ). Calculating the first order derivative ofπ(θ) with respect toθand simplification, we obtain (20) (21) where (22) (23) (24) Proof Letπbe a function ofW, i.e.,π=π(W). Calculating the first order and second order derivative ofπ(W) with respect toWand simplification, we obtain (25) (26) where (27) (28) (29) Proof By Eq.(25), we obtain (30) Therefore, the value ofθis determined byWsolely. Substituting Eq.(30) into Eq.(20), we obtain By the proof process of Theorem 2, we know that the solution of equationχ(W)=0 exists and is unique in [0,+∞) whenθ∈[θ′,θmax], where (31) We assume that the values of parameters in this model are as follows:θmin=0.1,θmax=0.9,δ=0.01,A=100 dollar,B=150 dollar,k=0.15,SP=95 dollar,MC0=15 dollar,MC1=1 dollar,R1=8 dollar,R2=10 dollar,k1=1500,a=1.2,k2=2.8 month,b=0.6,α=0.02, andT=2 month. To find the impact of reliability of the production process on the development cost and the total profit, we take the production reliability as decision variability. By Eq.(1) and Eq.(19), we letW=12 month and use the previous values of parameters, we obtain the optimal productθ*=0.25 with maximal profitπ*=2669 dollar by Matlab 7.0(see Fig.1). By Theorem 1, the optimal solution is the global optimal solution. From Fig.1, when manufacturers take some measures to improve the reliability of the production process(i.e., they lower the value of production reliability, even though that will result in a higher development cost), the manufacturers achieve higher profits and reach the maximal profit atθ*=0.25. However, after that, if manufacturers continue to increase investment in the reliability of production process, the development cost will directly increase and the total profit will decrease. Consequently, the model can be used to help manufacturers draw up an effective investment policy regarding the reliability of production process. Fig.1 Production reliability vs. total profit and development cost To assess the impact of the warranty length on both the warranty cost and the total profit, we take the warranty length as decision variability. By the expected warranty costR2θWDand Eq.(19), we letθ=0.30 and use the previous values for the parameters. We obtain the optimal warranty lengthW*=18.6 month with the maximum profitπ*=2399 dollar by Matlab 7.0 (see Fig.2). By Theorem 2, the optimal solution is the global optimal solution. From Fig.2, we can see that the warranty cost increases when the warranty length increases. In the interval [0,18.6], the total profit increases when warranty length increases. The total profit is maximized atW*=18.6 month. The manufacturers often increase the sale volume by giving a longer warranty length. But when the warranty length is greater than 18.6 month, the warranty cost will increase and the total profit will decrease. Therefore, this model can be used to help the manufacturers determine an optimal product warranty length with maximum profit. Fig.2 The warranty length vs. the total profit and warranty cost The manufacturers often take some measures to obtain more profit, and those measures not only impact the optimal product reliability but also impact the optimal warranty length. To understand the phenomenon clearly, we take both the product reliability and warranty length as decision variables. By Eq.(19), and using the previous values of parameters, we obtain the maximum profitπ*=2247 dollar atθ*=0.22 andW*=21.58 month by Matlab 7.0 (see Fig.3). Fig.3 Total profit vs. warranty length and production reliability From Fig.3, we know that the optimal solution (θ*,W*) is the global optimal solution. Hence, the model can be used to help the manufacturers create an effective policy to improve their profits when both the reliability of the production process and warranty length are considered. The sensitivity analysis of key parameters is in Tab.1. Tab.1 Sensitivity analysis of key parameters % From Tab.1, we can see clearly that the impact of the parameters change value on the optimal production reliability, optimal warranty length and the maximum total profit. For instance, the change of parameterk2has impacts on the optimal warranty lengthW*but not on the optimal production reliabilityθ*. As the parameterkdecreases,W*increases and can attract more consumers. As a result,θ*must decrease (implying a more reliable production process) to reduce the warranty cost and increase profit. Consequently, the model can be used for the manufacturers to improve the production process and make an optimal warranty sale policy with profit maximization. In an imperfect production process, the manufacturers need to decide what is their optimal production reliability and product warrant length. The model constructed in this paper can be used for the manufacturers to make effective investment policies to succeed when competing with similar products. The sale price is fixed for a fixed period. So, the product quality is very important in the competitive market. Product quality is related to the reliability of the production process. Thus, the model is useful for determining an optimal production reliability for the manufacturers who sell their products with warranties. Longer warranty length is an effective strategy to improve the sale volume, because it often implies higher product quality. However, too long warranty length results in higher expected warranty costs and lower profits. Therefore, it is very important to make an optimal warranty sale policy with profit maximization. The model can be used to solve the proposed problems. Both the reliability of production process and warranty length have impact on the total profit. From Tab.1, we can see that this model can also guide the manufacturers in their strategic planning to maximize their profits. [1]Yeh R H, Ho W T, Tseng S T. Optimal production run length for products sold with warranty[J].EuropeanJournalofOperationalResearch, 2000, 120(3): 575-582. [2]Chen C K, Lo C C. Optimal production run length for products sold with warranty in an imperfect production system with allowable shortages[J].MathematicalandComputerModeling, 2006, 44(3/4): 319-331. [3]Wu C C, Chou C Y, Huang C. Optimal price, warranty length and production rate for free replacement policy in the static demand market[J].Omega, 2009, 37(1): 29-39. [4]Giri B C, Dohi T. Inspection scheduling for imperfect production processes under free repair warranty contract[J].EuropeanJournalofOperationalResearch, 2007, 183(1): 238-252. [5]Tsao Y C. Determination of production run time and warranty length under system maintenance and trade credits[J].InternationalJournalofSystemsScience, 2012, 43(12): 2351-2360. [6]Huang H Z, Liu Z J, Murthy D N P. Optimal reliability, warranty and price for new products[J].IIETransactions, 2007, 39(8): 819-827. [7]Glickman T S, Berger P D. Optimal price and protection period decisions for a product under warranty[J].ManagementScience, 1976, 22(12):1381-1390. [8]Tsao Y C, Chen T H, Zhang Q H. Effects of maintenance policy on an imperfect production system under trade credit[J].InternationalJournalofProductionResearch, 2013, 51(5): 1549-1562. [9]Rosenblatt M J, Lee H L. Economic production cycles with imperfect production processes[J].IIETransactions, 1986, 18(1): 48-55. [10]Liao G L, Sheu S H. Economic production quantity model for randomly failing production process with minimal repair and imperfect maintenance[J].InternationalJournalofProductionEconomics, 2011, 130(1):118-124. [11]Maiti M K, Maiti M. Production policy for damageable items with variable cost function in an imperfect production process via genetic algorithm[J].MathematicalandComputerModelling, 2005, 42(9/10):977-990. [12]Sana S S A. production-inventory model in an imperfect production process[J].EuropeanJournalofOperationalResearch, 2010, 200(2): 451-464. [13]Sarkar B. An inventory model with reliability in an imperfect production process[J].AppliedMathematicsandComputation, 2012, 218(9): 4881-4891. [14]Guchhait P, Maiti M K, Maiti M. Production-inventory models for a damageable item with variable demands and inventory costs in an imperfect production process[J].InternationalJournalofProductionEconomics, 2013, 144(1):180-188. [15]Mettas A. Reliability allocation and optimization for complex systems[C]//ProceedingsoftheAnnualReliabilityandMaintainabilitySymposium. Los Angeles, CA, USA, 2000:216-221. 不完美生产系统中最优生产可靠性和产品保证销售期决策模型 吴军建 王海燕 (东南大学经济管理学院, 南京 211189) 在不完美生产系统中,以制造商利润最大化为目标,建立了一个决策模型.该模型以生产可靠性和保证期为联合决策变量,考虑了一种产品保证销售策略,即需求依赖于产品保证期和销售价格.并且在不完美生产过程中产生的所有不合格品均以一定的成本返工成合格品.利用Euler-Lagrange方法对模型进行分析,证明了最优生产可靠性和保证期的存在唯一性.通过数值实例证实了模型的有效性,并就关键参数对最优解和最优目标值影响进行了敏感性分析. 不完美生产系统;保证期;生产可靠性;Euler-Lagrange方法 F252 Received 2014-02-16. Biographies:Wu Junjian(1986—), male, graduate; Wang Haiyan(corresponding author), male, doctor, professor, hywang@seu.edu.cn. s:The National Natural Science Foundation of China (No.71171049), the Scientific Innovation Research of College Graduates in Jiangsu Province (No.CXLX13-097). :Wu Junjian, Wang Haiyan.A decision model of optimal production reliability and warranty length in an imperfect production system[J].Journal of Southeast University (English Edition),2014,30(4):537-543. 10.3969/j.issn.1003-7985.2014.04.023 10.3969/j.issn.1003-7985.2014.04.023
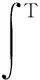

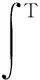



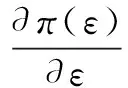


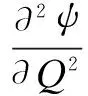
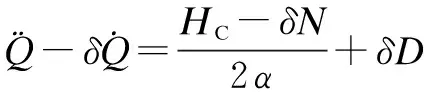
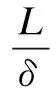

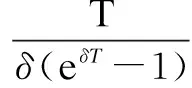
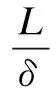

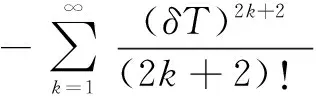
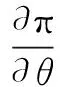
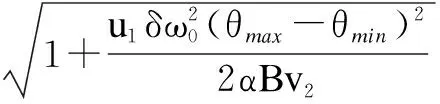
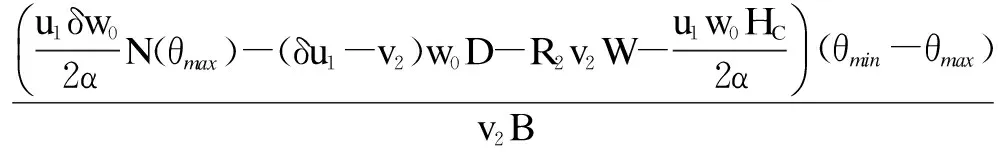

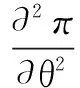
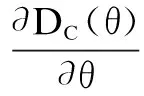


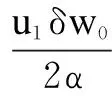
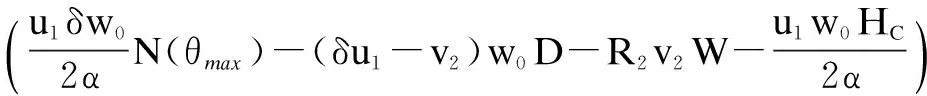
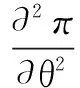
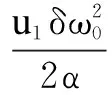
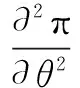
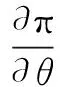
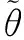


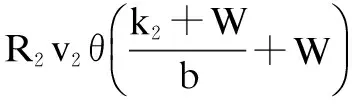
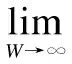

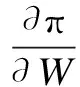
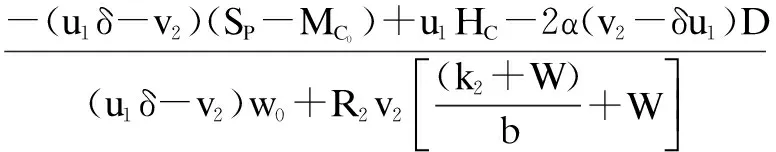
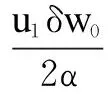
3 Numerical Example

4 Conclusion
 Journal of Southeast University(English Edition)2014年4期
Journal of Southeast University(English Edition)2014年4期
- Journal of Southeast University(English Edition)的其它文章
- Simulation of urban affordable housing land-use evolution based on CA-MAS model
- Dynamical chiral symmetry breaking in QED3
- Metal cation crosslinking of TiO2-alginate hybrid gels
- One-pot facile synthesis of highly photoluminescent graphene quantum dots with oxygen-rich groups
- Modeling household car ownership using ordered logistic regression model
- An automatic identification algorithm for freeway bottleneckbased on loop detector data
