Phase Transition and Physical Properties of InS∗

Hai-Yan Wang(王海燕),Xiao-Feng Li(李晓凤),Lei Xu(许磊), Xu-Sheng Li(李旭升),and Qian-Ku Hu(胡前库)

1School of Materials Science and Engineering,Henan Polytechnic University,Jiaozuo 454000,China

2College of Physics and Electronic Information,Luoyang Normal College,Luoyang 471022,China

1 Introduction

The III-VI compounds recently attracted considerable attention on account of their semiconducting nature and applications in optoelectronic devices,radiation detectors,and electrical switching.[1−2]Indium sul fi de is a member of III-VI family including GaS,GaSe,and InSe layered crystals. In the crystal,the In atoms have a tetrahedral coordination(three S atoms and one In atom),however,the two S atoms and one In atom are in one layer,the third S atom is in the neighboring layer.Therefore,the crystal structure of InS can be considered as a threedimensional network,which is somewhat different from a layered structure of its counterparts.For the InS crystal the temperature dependences of heat capacity,thermal expansion and isothermal compressibility coefficients,and the optical properties near the absorption edge are reported.[3]

However,reports on the properties of single crystal InS are scarce partly owing to the difficulty in growing single crystals and synthesizing the compound from its stoichiometric composition.[4−10]Takarabeet al.[11]have reported the high pressure Raman and transport measurement.Using uniaxial split-sphere apparatus the electrical resistance was studied at pressures up to 15 GPa,which indicates possible insulator-metal transition at high pressure due to changing in the band structure.InsituX-ray di ff raction has been used to study high pressure polymorphism of InS up to 13 GPa in the(293–573)K temperature range.[4]The phase transition fromPmnntoI4/mmmis found under isothermal compression at(7.5±0.5)GPa at the temperature of 293 K,and at(6.0±0.5)GPa at the temperature of 573 K.The variation of the Raman frequencies and the lattice parameters of InS as a function of pressure up to 30 GPa and 16 GPa have been reported,respectively.[5]And Anomalies in the pressure dependence of the Raman frequencies and rather rapid decrease of the lattice parameterbtoward a with pressure clearly indicated a phase transition at(5.0±0.3)GPa.However,it is unclear if InS system is monoclinic or orthorhombic.[4,12]

Therefore,in the present work,the crystal structures of InS under high pressures are extensively explored based on a global free energy minimization merging the first-principle calculations by particle swarm optimization algorithm technique implemented in CALYPSO(Crystal Structure Analysis by Particle Swarm Optimization)code.[13−14]Three phases(a ground state phase orthorhombicPnnm,monoclinic phaseC2/m,and cubicPm-3mphase)under high pressures for InS have been uncovered.The electronic properties and phonon dispersion of InS under different pressure have been further researched.

2 Computational Methods

Extensive structure searches over InS at 0 GPa,10 GPa,20 GPa,30 GPa,40 GPa,50 GPa,80 GPa,and 100 GPa with 1–4 formula units(f.u.) for each simulation cell was performed using the PSO technique in the CALYPSO code.[13−14]The structural relaxation and electronic band structure calculations were carried out based on density functional theory with the Perdew-Burke-Ernzerh of(PBE)generalized gradient approximation(GGA)of the exchange-correlation energy as implemented in the VASP code.[15]The projector augmented wave(PAW)method was used to model the electron-ion interaction,including the 5 s,5 p states and 3 s,3 p states of In and S,respectively,in the valence space.A kinetic energy cuto ffof 420 eV was used for the plane-wave basis set.A dense k-point grid with the spacing of 2π×0.04◦A was used to sample the Brillouin zone and shown to yield excellent convergence for total energies.The phonon calculation was carried out according to a fi nite displacement approach through the PHONOPY code.[16]

3 Results and Discussions

The structural search at ambient pressure for the stoichiometric InS predicts an orthorhombic phase ofPnnmspace group,as shown in Fig.1(a).There are 4 f.u.in the unit cell inPnnmphase(at zero pressurein which two inequivalent atoms In and S occupy the Wycko ff4g(−0.124 33,0.119 24,0.500 00)and 4g(−0.965 49,0.346 82,0.500 00)sites,respectively.The searched structure at atmospheric pressure is consistent with experimental ones from Ref.[4]and Ref.[12].With the pressure up to about 29.5 GPa,the most stable crystal structure isPm-3mphase(Fig.1(b)).The calculated lattice constants area=b=c=3.18◦A at 29.5 GPa,and the In and S atom positions are 1a(0.000 00,0.000 00,0.000 00)and 1b(0.500 00,0.500 00,0.500 00).The In-S bond length is 2.75at 29.5 GPa.In the process of searching structures using CALYPSO under different pressures,we also obtained a metastable phaseC2/m,as shown in Fig.1(b).The occupied Wycko ffpositions are 2b(0.000 00,0.500 00,0.000 00)and 2c(0.500 00,0.500 00,0.500 00)for In and S.The cylinders in crystal structure are very similar to that inP63/mmcphase.The enthalpy difference between thePm-3mphase andC2/mphase is very small,therefore in the following work we also studied the properties ofC2/mmetastable phase.

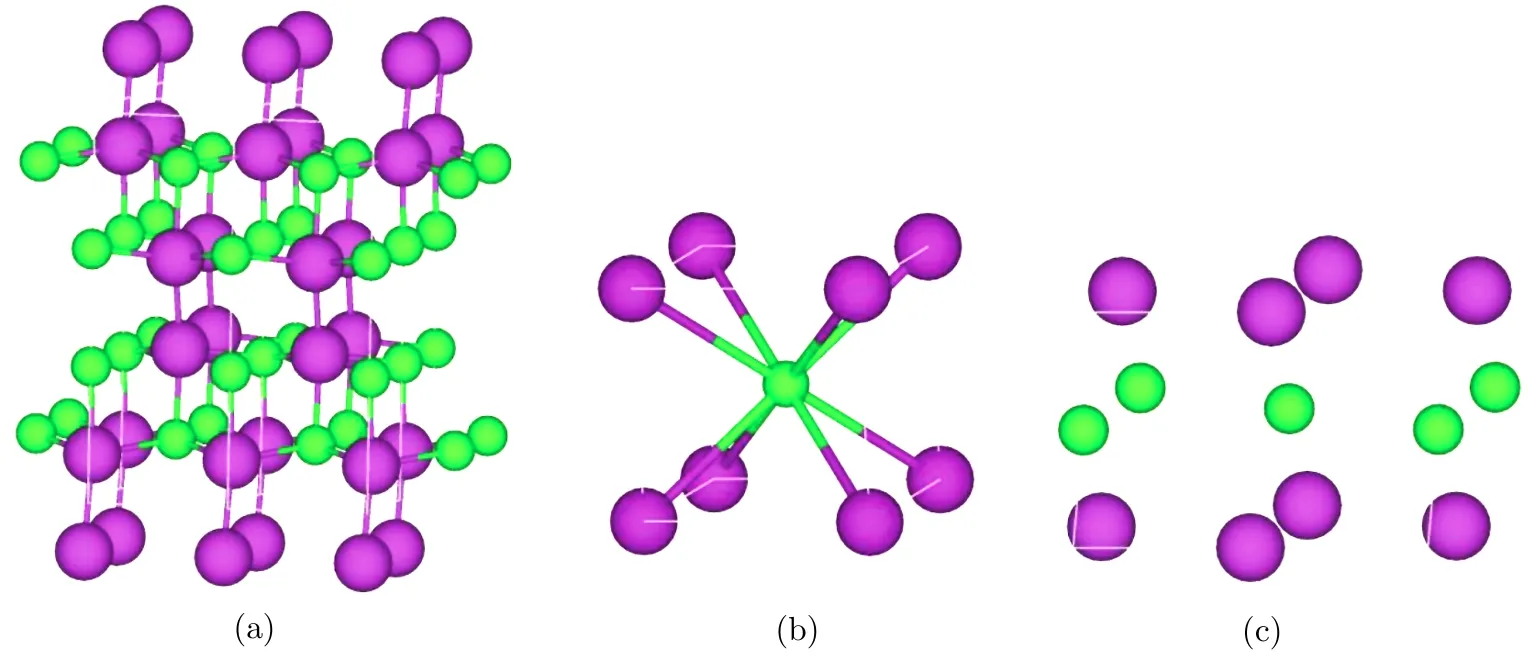
Fig.1 (Color online)Crystal structure of InS.The purle and green spheres represent In and S atoms,respectively.(a)Pnnm phase(b)Pm-3m phase(c)C2/m phase.

Fig.2 The calculated enthalpies per atom of four structures of InS relative to Pm-3m phase as a function of pressures range from(20–45)GPa.

In order to investigate the phase transformation of InS under different pressure,we plot the enthalpy differences of InS with different structures relative toPm-3mphase in the pressure wide from 20 GPa to 45 GPa in Fig.2.It is obvious that the enthalpy ofPnnmphase is lower than that ofPm-3mphase when the pressure is below about 29.5 GPa at 0 K,andPnnmphase is the ground state stable structure.From Fig.2,we find that pressure stimulates InS going through phase transition fromPnnmphase toPm-3mphase at about 29.5 GPa.For the experimental research on the phase transition of InS under high pressures,only Kabalkinaet al.[4]found the phase transition fromPnnmphase toI4/mmmone at(7.5±0.5)GPa and 293 K.The enthalpy differences of InS withI4/mmmphase relative toPm-3mone under different pressures are also shown in Fig.2.But from the calculated results at 0 K theI4/mmmphase is an unstable phase at the pressure below 45 GPa.And further the enthalpy differences of InS betweenI4/mmmphase andPnnmphase arrived at more 80 meV.Therefore,the phase thansformation of InS fromPnnmtoI4/mmmphase is very difficult based on the theoretical results.

Fig.3 The phonon-dispersion curves of InS at ambient pressure(a)Pnnm phase(b)C2/m phase(c)Pm-3m phase(d)I4/mmm phase.

Fig.4 Calculated electronic band structures for InS(a)Pnnm phase at 0 GPa(b)C2/m phase at 29.5 GPa(c)Pm-3m phase at 29.5 GPa.

To check the dynamical stabilities of the currently predicted phases of InS,the phonon dispersion curves have been calculated and shown in Fig.3.There are not any imaginary phonon frequencies in the whole Brillouin zone forPnnm-InS,C2/m-InS,andPm-3m-InS,which proves that the three phases are dynamical stable at ambient condition.The higher phonon frequencies are often caused by shorter bond lengths.And further,it is easily found that the phonon frequencies ofC2/m-InS andPm-3m-InS shown in Fig.3 are larger than that ofPnnm-InS,which indicates that the bond lengths ofC2/m-InS andPm-3m-InS are shorter than that ofPnnmphase.The imaginary phonon frequency exiting inI4/mmmphase denotes it is an unstable phase,which is consistent with the calculated enthalpy results shown in Fig.2.

In order to further understand the electronic properties of InS in detail,we also calculate the band structures in the studied pressure range.The obtained electronic band structures for InS withPnnmphase at 0 GPa,C2/mphase andPm-3mphase at 29.5 GPa are shown in Figs.4(a)–4(c). Our calculated band gap value for InS withPnnmstructure at 0 GPa is about 2.08 eV,which agrees well with the experimental reported band gap value 2.09 eV.[12]The reported band gap of single crystalβ−ln2S3is in the range of(2–2.4)eV,whereas the one of polycrystallineβ−ln2S3is in the range from 2 eV to 3.7 eV.[17]The calculated band structures ofC2/mphase andPm-3mphase at 29.5 GPa are shown in Figs.4(b)and 4(c).Moreover,the electronic structure suggests that theC2/mandPm-3mphases are metallic phases.

4 Conclusions

In summary,the missing structures for InS under different pressures were unraveled by structure prediction based on first-principles calculations.Three phases(Pnnm,C2/mandPm-3mphases)of InS under pressures are established.Among themC2/mphase is a metastable phase.The three phases are proved to be dynamical stable at ambient condition based on the calculated enthalpies and phonon dispersions.Our calculated band gap value for InS withPnnmstructure at 0 GPa is about 2.08 eV,which agrees well with the experimental value.Moreover,the electronic structure suggests that theC2/mandPm-3mphase are metallic phases.Phase transformation fromPnnmphase toPm-3mphase is firstly found at the pressure of about 29.5 GPa.

[1]N.B.Singh,R.Narayanan,A.X.Zhao,et al.,Mater Sci.Eng.B 49(1977)243.

[2]F.Adduci,M.Ferrara,P.Tantalo,et al.,Phys.Status Solidi a.15(1973)303.

[3]N.G.Aliev,I.G.Kerimov,and M.M.Kurbanov,Ter-modinamickeskie Svoistva Metallicheskikh Splavov,Azerb.Gos.Izd,Baku(1975).

[4]S.S.Kabalkina,V.G.Losev,and N.M.Gasanly,Solid State Commun.44(1982)1383.

[5]U.Schwarz,A.F.Goncharov,and K.Syassen,High Pressure Science and Technology,Proc.Joint XV AIRAPT and XXXIII EHPRG,Int.Conf.,Singapore(1996)427.

[6]N.M.Gasanly,H.özkan,A.Aydinli,et al.,Solid State Commun.110(1999)231.

[7]A.F.Qasrawi and N.M.Gasanly,Semicond.Sci.Technol.17(2002)1288.

[8]N.M.Gasanly and A.Aydinli,Solid State Commun.101(1997)797.

[9]F.E.Faradzhev,N.M.Gasanly,and A.S.Ragimov,Solid State Commun.39(1981)587.

[10]T.Nishino,K.Taniguchi,and Y.Hamakawa,Solid State Commun.19(1976)635.

[11]K.Takarabe,K.Wakamura,and E.Ito,Solid State Commun.46(1983)215.

[12]P.Kushwaha,A.Patra,E.Anjali,et al.,Opt.Mater.36(2014)616.

[13]Y.C.Wang,J.Lv,L.Zhu,et al.,Phys.Rev.B 82(2010)094116.

[14]Y.C.Wang,J.Lv,L.Zhu,et al.,Comput.Phys.Commun.183(2012)2063.

[15]G.Kresse and D.Joubert,Phys.Rev.B 59(1999)1758.

[16]A.Togo,F.Oba,and I.Tanaka,Phys.Rev.B 78(2008)134106.

[17]N.Barreau,Solar Energy 83(2009)363.