Thermodynamic Geometry of Charged AdS Black Hole Surrounded by Quintessence∗

Shao-Wen Wei(魏少文), Qing-Tao Man(满清涛),and Hao Yu(喻豪)

Institute of Theoretical Physics,Lanzhou University,Lanzhou 730000,China

1 Introduction

Black hole thermodynamics continues to be an interesting and important subject in gravitational physics.Recently,in anti-de Sitter(AdS)space,the black hole phase transitions,such as the Hawking-Page phase transition and small-large black hole phase transition,have gained much attention.[1−7]

The black hole phase transitions can also be explored with the thermodynamic geometry.The first thermodynamic geometry was proposed by Weinhold several decades ago.[8]He suggested that a thermodynamic geometry metric can be calculated as the second derivatives of internal energyUwith respect to the entropySand other extensive quantities of a thermodynamic system.A few years later,Ruppeiner constructed another geometry into the thermodynamics.[9]different from the Weinhold one,the thermodynamic potential of the Ruppeiner geometry is chosen to be the entropySrather than the internal energyU.However,these two geometries are proved to be conformally related to each other.For the ideal gas and the van der Waals(vdW)gas,the Ruppeiner geometry is carried out.The result shows that the curvature vanishes for the ideal gas.While for the vdW gas,its curvature is non-zero and diverges only at the point,where the phase transition takes place.[10]For various black holes and black branes,the Weinhold geometry and Ruppeiner geometry have been extensively investigated.[10−40]

The issue of thermodynamic metrics and black hole phase transitions is reconsidered in Ref.[41].Based on the Hessian matrix of several free energy,a new thermodynamic metric is introduced.They further investigate the thermodynamic metrics on all thermodynamic potentials generated by Legendre transformations.And the correspondences between the curvature singularities and the divergence of the specific heat are discussed.Moreover,for general case,the correspondence of phase transition points and singularities of thermodynamic geometry of black holes is examined in Ref.[42].Such correspondence is also proved by employing the Nambu brackets.[43]The conformal transformations that connect different thermodynamic metrics are also given.

Very recently,it is showed that,[44]in the presence of the quintessence,the charged AdS black hole exhibits a small-large black hole phase transition,which is similar to the liquid-gas phase transition of vdW fluid.Near the critical point,the heat capacity will diverge.It also shares the same critical phenomena and scaling law.So,in this paper,we would like to investigate the thermodynamic geometry and the phase transition for the black hole.

The paper is organized as follows.In Sec.2,we review some thermodynamic quantities of the charged AdS black hole surrounded by quintessence.In Sec.3,three different thermodynamic geometries are introduced,and the corresponding curvatures are calculated.Finally,the paper ends with a brief summary.

2 Thermodynamics of the Black Hole

In the presence of the quintessence,the line element of a charged AdS black hole is[45]

Here the parametersM,Q,and Λ are,respectively,related to the black hole mass,charge and cosmological constant.ωis a state parameter,andacorresponds to a normalization factor in the density of the quintessence,

Treating state parameteraas a new thermodynamic quantity,the first law of the black hole is

Fig.1 Behavior of the heat capacity with a=0.1,ω=−2/3,and Q=1.(a)P=0.003,(b)P=0.0033,and(c)P=0.004.

In Fig.1,we plot the behavior of the heat capacity fora=0.1,ω=−2/3,andQ=1.For low pressure shown in Fig.1(a),we can see that there are two divergence points.And in the first and third regions,the heat is positive,which implies that the black hole system is stable.

While for the second region,the heat is negative,which means that the black hole system is unstable in that parameter range.When the pressure approaches the valueP=0.0033,(see Fig.1(b)),the heat goes to positive in fi nity only atS=18.85.This case is just the critical case.Further increasing the pressure such thatP=0.004,the divergence behavior vanishes,and there will be only a peak,which indicates that there is no phase transition.

3 Thermodynamic Geometries of the Black Hole

In the above section,we show that such black hole exhibits an interesting phase transition.Here we would like to consider the thermodynamic geometries for the black hole.

In general,there are several different kinds of geometries.And it is thought that the phase transition information is included in the scalars constructed with the thermodynamic geometries.In the following,we will examine three geometries,Weinhold geometry,Ruppeiner geometry,and free energy geometry.For simplicity,we seta=1 andω=−2/3.Taking such choice,the mass,temperature,and heat capacity will be

3.1 Weinhold Geometry

For the Weinhold geometry,the thermodynamic potential is chosen as the black hole mass M.The line element for this black hole is

The Christ off el symbol is calculated with

The behavior of the Weinhold curvature is given in Fig.2.For different pressureP,it is always negative.There are two divergence points for P=0.008 and one divergence point for P=0.0099.And aboveP>0.0099,the divergence behavior disappears.Such case is very similar to that of the heat capacity.However,the critical point does not meet that of the heat capacity.Nevertheless,it gives us a hint for another phase transition.

3.2 Ruppeiner Geometry

Ruppeiner geometry is also an alternative.different from the Weinhold geometry,the thermodynamic potential here is the entropySrather than the black hole massM.Similar to the Weinhold geometry,the line element of the Ruppeiner geometry can be obtained with

withx1=Mandx2=Q.Recalling that there exists a conformal relation between the Weinhold geometry and Ruppeiner geometry,we have

Considering such relation,we can obtain the metric functions for the Ruppeiner geometry from Eq.(24),

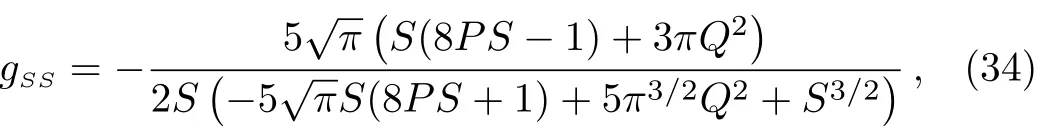
Note that we have made a parameter change from(M,Q)to(S,Q).After a tedious calculation,we get the Ruppeiner curvature

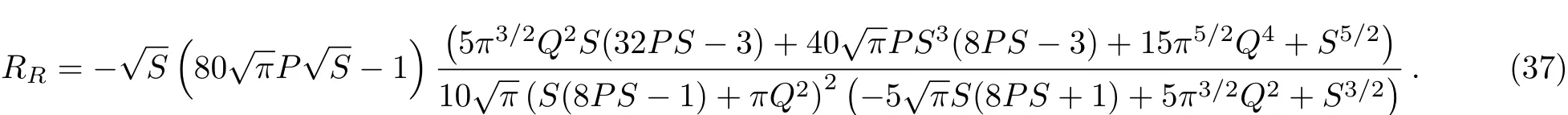
From this expression,we can find that the Ruppeiner curvature also diverges at the point where the Weinhold curvature does,i.e.,Besides,it also diverges at the point given in Eq.(18),which is just related to the extremal black hole with vanished temperature.So apart from the extremal black hole,the Ruppeiner curvature has the same divergence behavior as that of the Weinhold curvature,and thus the information of phase transition may be re fl ected from it.The detailed behavior of the Ruppeiner curvature can also be found in Fig.3 for different parameter ranges.

Fig.2 Behavior of the Weinhold curvature with a=0.1,ω=−2/3,and Q=1.(a)P=0.008,(b)P=0.0099,and(c)P=0.0120.

Fig.3 Behavior of the Ruppeiner curvature with a=0.1,ω=−2/3,and Q=1.(a)P=0.008,(b)P=0.0099,and(c)P=0.0120.

3.3 Free Energy Geometry

Free energy geometry can also give us some information about the black hole phase transition.Now let us turn to the free energy geometry.The free energy for this black hole is

for fixed pressureP.Then the element will be of the form

Here it is convenient to adopt the variables(S,Q)to calculate the curvature.After the choice,one can get the metric functions

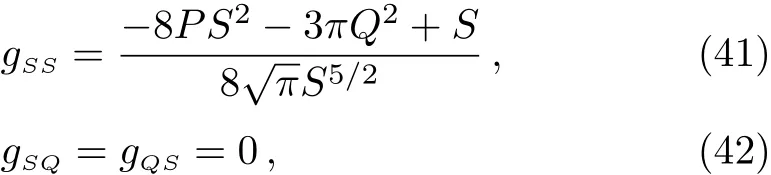
For this case,one can easily work out the free energy curvatureRG,which reads

It is clear that the free energy curvatureRGdiverges at the point where the heat capacity diverges.For the entropyS>1/4P,RGis positive,and forS<1/4P,it will be negative.While whenS=1/4P,the curvature vanishes.Takinga=0.1,ω=−2/3,andQ=1,we plot the free energy curvatureRGin Fig.4 forP=0.003,0.0033,and 0.004,respectively.In Fig.4(a),there are two divergence points atS=14.41 and 27.26,at which both the curvatures go to negative infinity.For the critical pressureP=0.0033,the two divergence points meet each other and only one divergence behavior appears atS=6π.Increasing the pressure above this value,the divergence behavior will disappear(see Fig.4(c)withP=0.004).Thus,the free energy geometry can be used to explore the phase transition through its divergence behavior.On the other hand,taking the pressureP=0,it will reduce to the result of Ref.[40].

Fig.4 Behavior of the free energy curvature with a=0.1,ω=−2/3,and Q=1.(a)P=0.003,(b)P=0.0033,and(c)P=0.004.

4 Summary

We have studied the thermodynamic geometry for the charged AdS black hole surrounded by quintessence.First,the heat capacity is obtained,and its divergence points are also calculated.For low pressure,the heat capacity is found to have two divergence points.And these two points coincide with each other at a critical value of the pressure.Above the value,no divergence behavior appears.These divergence behaviors are closely related to phase transition.

Then, three thermodynamic geometries are constructed and the corresponding curvatures are calculated.The Weinhold curvature is found to be negative.And it has two divergence behaviors.Similar to the heat capacity,these two divergence points meet each other at one critical pointP=1/32πQ2,which is larger than that of the heat capacity,i.e.,P=1/96πQ2.To some extent,this divergence behavior of the Weinhold curvature also implies a phase transition.

The Ruppeiner curvature is also obtained.It shares the same divergence points with the Weinhold curvature.So it encodes the same information of the phase transition as that of the Weinhold curvature.Moreover,the Ruppeiner curvature also diverges atT=0,implying a phase transition between a non-extremal black hole and an extremal black hole.

At last,we dealt with the free energy geometry.The result shows that the curvature has the same divergence behavior as the heat capacity.So the phase transition information included in the heat capacity can also be found from the free energy geometry.

[1]S.W.Hawking and D.N.Page,Commun.Math.Phys.87(1983)577.

[2]E.Witten,Adv.Theor.Math.Phys.2(1998)505.

[3]A.Chamblin,R.Emparan,C.V.Johnson,and R.C.Myers,Phys.Rev.D 60(1999)064018.

[4]A.Chamblin,R.Emparan,C.V.Johnson,and R.C.Myers,Phys.Rev.D 60(1999)104026.

[5]M.M.Caldarelli,G.Cognola,and D.Klemm,Class.Quant.Grav.17(2000)399.

[6]R.Banerjee and D.Roychowdhury,J.High Energy Phys.1111(2011)004.

[7]R.Banerjee,S.K.Modak,and D.Roychowdhury,J.High Energy Phys.1210(2012)125.

[8]F.Weinhold,J.Chem.Phys.63(1975)2479.

[9]G.Ruppeiner,Phys.Rev.A 20(1979)1608.

[10]G.Ruppeiner,Rev.Mod.Phys.67(1995)605;ibid.68(1996)313(E).

[11]S.Ferrara,G.W.Gibbons,and R.Kallosh,Nucl.Phys.B 500(1997)75.

[12]R.G.Cai and J.H.Cho,Phys.Rev.D 60(1999)067502.

[13]J.Aman,I.Bengtsson,and N.Pidokrajt,Gen.Rel.Grav.35(2003)1733.

[14]D.A.Johnston,W.Janke,and R.Kenna,Acta Phys.Polon.B 34(2003)4923.

[15]G.Arcioni and E.Lozano-Tellechea,Phys.Rev.D 72(2005)104021.

[16]J.Y.Shen,R.G.Cai,B.Wang,and R.K.Su,Int.J.Mod.Phys.A 22(2007)11.

[17]J.E.˚Aman,I.Bengtsson,and N.Pidokrajt,Gen.Rel.Grav.38(2006)1305.

[18]J.E.˚Aman and N.Pidokrajt,Phys.Rev.D 73(2006)024017.

[19]B.Mirza and M.Zamaninasab,J.High Energy Phys.0706(2007)059.

[20]J.E.˚Aman,N.Pidokrajt,and J.Ward,EAS Publ.Ser.30(2008)279.

[21]A.J.M.Medved,Mod.Phys.Lett.A 23(2008)2149.

[22]Y.S.Myung,Y.W.Kim,and Y.J.Park,Phys.Lett.B 663(2008)342.

[23]Y.H.Wei,Phys.Rev.D 80(2009)024029.

[24]R.Biswas and S.Chakraborty,Gen.Rel.Grav.42(2010)1311;ibid.R.Biswas and S.Chakraborty,Astrophys.Space Sci.326(2010)39.

[25]T.Sarkar,G.Sengupta,and B.N.Tiwari,J.High Energy Phys.0810(2008)076.

[26]S.Bellucci and B.N.Tiwari,Entropy 12(2010)2097.

[27]J.E.˚Aman,J.Bedford,D.Grumiller,et al.,J.Phys.Conf.Ser.66(2007)012007.

[28]G.Ruppeiner,Phys.Rev.D 78(2008)024016.

[29]S.W.Wei,Y.X.Liu,Y.Q.Wang,and H.Guo,Europhys.Lett.99(2012)20004.

[30]S.W.Wei and Y.X.Liu,Phys.Rev.D 87(2013)044014.

[31]S.W.Wei and Y.X.Liu,Phys.Rev.Lett.115(2015)111302.

[32]Y.H.Wei,X.Cui,and J.X.Zhao,Commun.Theor.Phys.65(2016)28.

[33]R.Banerjee,B.R.Majhi,and S.Samanta,Phys.Lett.B 767(2017)25.

[34]K.Bhattacharya and B.R.Majhi,Phys.Rev.D 95(2017)104024.

[35]H.Quevedo and A.Sanchez,Phys.Rev.D 79(2009)024012.

[36]H.Quevedo and A.Sanchez,J.High Energy Phys.0809(2008)034.

[37]H.Quevedo and A.Sanchez,Phys.Rev.D 79(2009)087504.

[38]J.L.Zhang,R.G.Cai,and H.Yu,J.High Energy Phys.1502(2015)143.

[39]J.L.Zhang,R.G.Cai,and H.Yu,Phys.Rev.D 91(2015)044028.

[40]M.Azreg-Ainou and M.E.Rodrigues,J.High Energy Phys.09(2013)146.

[41]H.Liu,H.Lu,M.Luo,and K.N.Shao,J.High Energy Phys.1012(2010)2010.

[42]S.A.H.Mansoori and B.Mirza,Eur.Phys.J.C 74(2014)2681.

[43]S.A.H.Mansoori,B.Mirza,and M.Fazel,J.High Energy Phys.04(2015)115.

[44]G.Q.Li,Phys.Lett.B 735(2014)256.

[45]V.V.Kiselev,Class.Quant.Grav.20(2003)1187.