Preference-based multiobjective artificial bee colony algorithmfor optimization of superheated steam temperature control
Zhou Xia Shen Jiong Li Yiguo
(1School of Energy and Environment, Southeast University, Nanjing 210096, China)(2School of Mechanical and Electrical Engineering, Jinling Institute of Technology, Nanjing 211169, China)
Preference-based multiobjective artificial bee colony algorithmfor optimization of superheated steam temperature control
Zhou Xia1,2Shen Jiong1Li Yiguo1
(1School of Energy and Environment, Southeast University, Nanjing 210096, China)(2School of Mechanical and Electrical Engineering, Jinling Institute of Technology, Nanjing 211169, China)
In order to incorporate the decision maker’s preference into multiobjective optimization, a preference-based multiobjective artificial bee colony algorithm (PMABCA) is proposed. In the proposed algorithm, a novel reference point based preference expression method is addressed. The fitness assignment function is defined based on the nondominated rank and the newly defined preference distance. An archive set is introduced for saving the nondominated solutions, and an improved crowding-distance operator is addressed to remove the extra solutions in the archive. The experimental results of two benchmark test functions show that a preferred set of solutions and some other non-preference solutions are achieved simultaneously. The simulation results of the proportional-integral-derivative (PID) parameter optimization for superheated steam temperature verify that the PMABCA is efficient in aiding to making a reasonable decision.
preference; multiobjective; artificial bee colony; superheated steam temperature control; optimization
Superheated steam temperature plays an important role in the security and economy of power plants. It is well known that time delay makes it difficult to control. In order to solve the large time delay problem, a cascade control system is usually employed to control the superheated steam temperature[1-2]. The objective of the inner loop controller is to quickly respond to spray water flow disturbances, and it is usually designed as a proportional controller. The primary control object is characterized by hysteresis and nonlinearity, and a proportional-integral-derivative (PID) controller is usually employed[3]. Clearly, it is quite difficult to tune the PID gains because of the time delay and nonlinearities.
The common performance indices used by the PID controllers are the rising timetr, the settling timets, the maximum overshootσ, the attenuation rateψ, and different error criteria[4], such as the integral of absolute value of error (IAE), integral of squared error(ISE), integral time multiplied by the absolute value of error (ITAE), integral time multiplied by the squared error (ITSE), etc. In recent literature, many experimental results have proved that there are conflicts among these objectives[5-6].
Researchers used different algorithms to search for the design parameters of the PID controller[5-6]. However, few of them incorporate the decision maker (DM)’s preference into the optimization. Since most multiobjective optimization algorithms supply the DM with a large number of solutions, it appears that it is a difficult task to choose the final preferred alternative. In practice, the DM often has at least a vague idea about what type of solutions is preferred. Thus, instead of the boring entire frontier, the emphasis may be put on finding a preferred and smaller set of optimal solutions.
Recently, the artificial bee colony (ABC) algorithm has been applied in many research studies due to its local and global search capability. The ABC algorithm which was developed by Karaboga, is based on the foraging behavior of honey bees[7]. In the ABC algorithm, every bee is regarded as an agent, and the swarm intelligence is employed in labor division, cooperation, and role conversion. The research results of Ref.[8] show that the ABC algorithm performs better than the genetic algorithm and the particle swarm algorithm in most cases. Taking both the DM’s preference and the efficiency of the ABC algorithm into consideration, a preference-based multiobjective artificial bee colony algorithm (PMABCA) is proposed in this paper.
1 Multiobjective Optimization
Generally, a multiobjective optimization problem can be described as
minf(X)=(f1(X),f2(X),…,fm(X))
(1)
s.t.gp(X)≥0p=1,2,…,l
hq(X)=0q=1,2,…,n
whereX∈Ωis the decision vector;gp(X)≥0 andhq(X)=0 are the constraints;Ωis the feasible region.
Nowadays, the most popular optimal concept used in multiobjective optimization is Pareto optimality. Its formal definitions can be described as follows[9]:
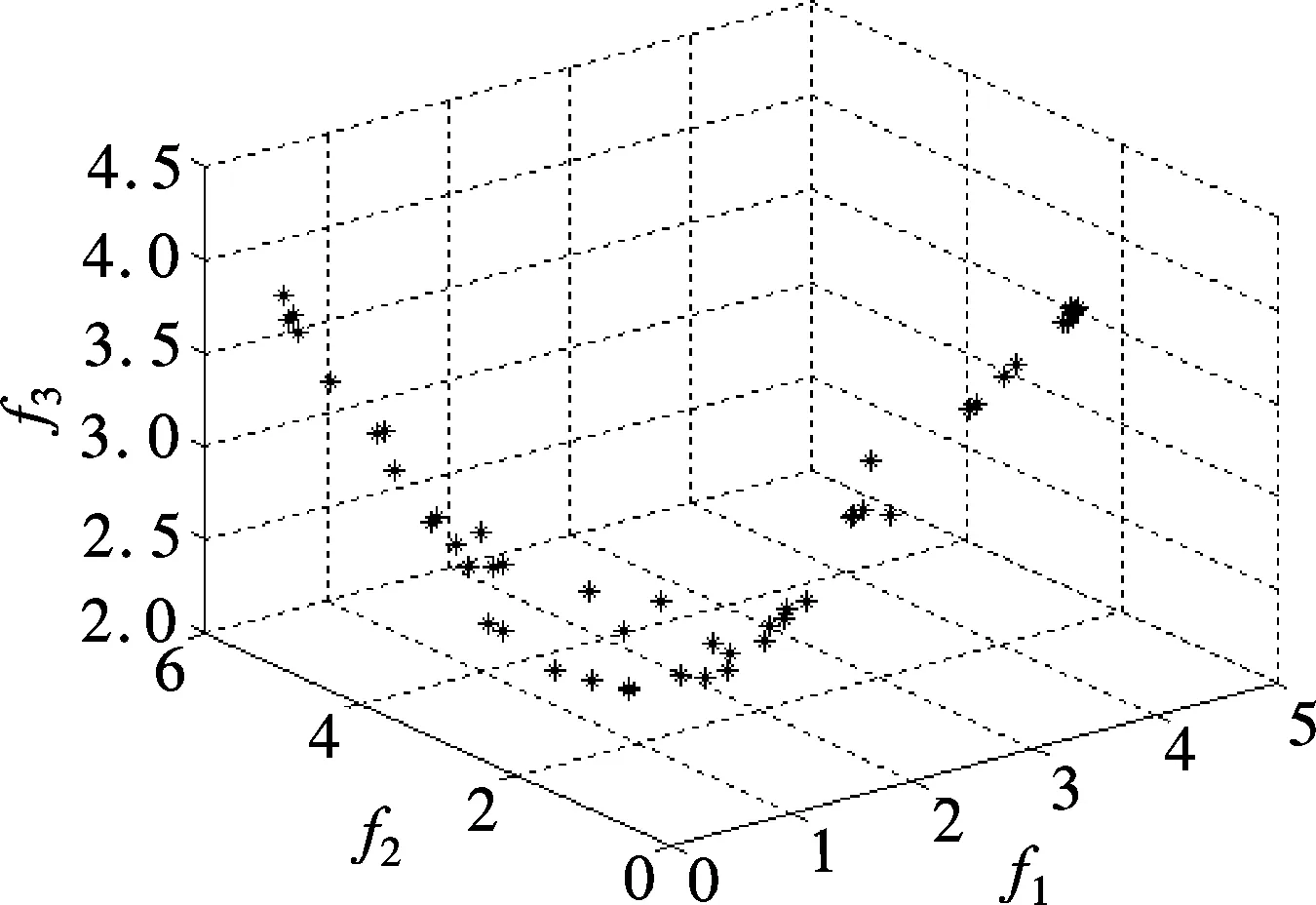
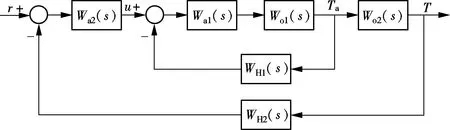
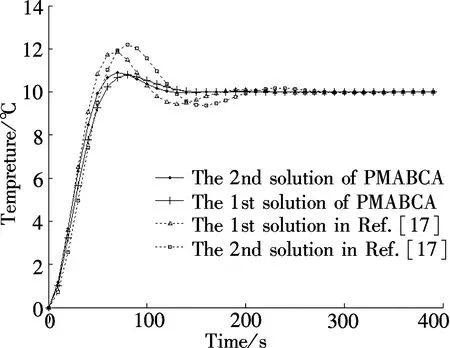
Definition 1 ∀Xi,Xj∈Ω, if ∀k∈{1,2,…,m},fk(Xi)≤fk(Xj); together with∃t∈{1,2,…,m},ft(Xi) Definition 2 ∀Xi,Xj∈Ω, if ∃k∈{1,2,…,m},fk(Xi) Definition 3Xi∈Ωis said to be a Pareto optimal solution if∃Xj∈Ω, s.t.Xj≻Xi. DenoteX*as the Pareto optimal solutions,PS={X*X∈{X*}} is said to be the Pareto optimal front. In the past decades, various methods have been proposed for expressing the DM’s preferences[10-12]. Among them, the reference point method seems to be a natural way to express preference. When using the reference point approach in practice, the DM is asked to supply a reference point and a weight vector. The reference point guides the search toward the desired region while the weight vector provides more detailed information about each objective. Recently, the Euclidean distance measure-based reference point approach addressed by Deb has been widely used in preference-based multiobjective optimization algorithms, which is described as[13] (2) With the Euclidean distance measure, a number of solutions in the region of interest will be found. However, the difference between the objective of each candidate and the relative objective of the reference point is not considered in Eq.(2). For example, suppose that the chosen reference point is (10,10) and the chosen weight vector is (0.5,0.5); solutionSais equal to (6.1,4.8); solutionSbis equal to (7.5,4); it is clear that the weighted Euclidean distance fromSaandSbto the reference point are equal. So it cannot be estimated which one is better with Eq.(2). But if we examine each objective in detail, we can see that there are differences between them. From the above discussion, it is necessary to consider the distance from each objective to the relative objective of the reference point. Nevertheless, how to secularize the multiobjectives in an equation remains unresolved. If we weight the difference of every objective in an equation, the weight vector is difficult to set and it is somewhat subjective. A simple method of taking the degree of each objective into consideration is to calculate the largest weighted distance difference among all the preference objectives. In this paper, a novel reference point-based preference expression method is addressed, with which not only the weighted largest distance of each objective to the relative one of the reference point being calculated, but also the weighted preference distance to the reference point simultaneously being taken into consideration. The new preference distance is calculated as follows: 1) Calculate the weighted largest difference of all preference objectives i,j∈1,2,…,p;i≠j;p≤m (3) wherepequals the number of objectives that the DM can express preference for, andwiis the weight coefficient. The more attention to the objective paid, the larger the coefficient value is. 2) Calculate the weighted preference distance of each candidate (4) 3) Calculate the preference distance of each candidate (5) If the value ofdp(x,r) is close to 0, it indicates that distances of the selected objectives to the reference point are similar to the corresponding dimension. In the proposed preference expression method, both the differences of each objective and the weighted preference distance to the reference point are considered. The solution near the reference point and the small deviations between the objectives are preferred. However, if we put the emphasis on objective-1 and set the weight coefficients as (0.75,0.25), we can obtaindp(a,r)>dp(b,r). In addition, if we put the emphasis on objective-2 and set the weight coefficients to be (0.25,0.75), we can obtaindp(a,r) Similar to the basic ABC algorithm, the PMABCA consists of three groups of bees: employed bees, onlooker bees, and scouts. A possible solution for the optimization problem is defined as a food source, and the fitness value of the solution is defined as the nectar amount of the associated food source. In the PMABCA, the number of employed bees and the number of onlooker bees are equal, and they are both equal to the number of food sources. Initially, each employed bee produces a new food source from its surrounding food source site and exploits the better one. In this study, in order to avoid the searching process from being trapped in the local optima, the simulated binary crossover (SBX) operator and the polynomial mutation (PM) operator[14]are introduced into the exploitation. After exploitation of the employed bees, information is passed onto the onlooker bees, which select food sources according to the quality of each solution. The onlooker bees exploit the same as the employed bees. The third group of bees are the scouts who are sent into the searching area randomly to discover a new food source when one has been abandoned. In order to keep the nondominated solutions in the searching process, an external archive is introduced into the PMABCA. As both the preference and non-preference solutions are kept in the same archive, an improved crowding distance (CD) operator is addressed to determine the best spread-out of solutions in the archive. Fig.1 presents the flowchart of the proposed algorithm. 3.1 Main operators of the PMABCA 3.1.1 Parameters and food sources initialization There are three parameters to be initialized, i.e., the number of food sourcesNS, the number of cycles through which a food source cannot be improved further before it is assumed to be abandoned (limit), and a termination criterion. In the first step, besides setting the parameters of the algorithm, the PMABCA will generate the initial food sources by using a random approach. LetXi={xi1,xi2,…,xid} represent thei-th food source in the population, wheredis the problem dimension. Each food source is generated as follows: Fig.1 Flowchart of the PMABCA (6) 3.1.2 Employed bees optimization At the stage of the employed bees’ optimization, each employed bee produces a new candidate food source in the neighborhood of its current position. After that, a greedy selection procedure is carried out to decide which one will be kept in the population. If the candidate solution can dominate the previous one, the employed bee will memorize the new position and forget the previous one. Otherwise, the employed bee discards the new solution and keeps the previous position in its memory. In order to generate good quality and diversity neighboring solutions, SBX and PM are introduced to generate promising solutions[14]. 3.1.3 Fitness assignment based on the preference distance After all the employed bees complete the local search process, they share the position information of the food sources with the onlookers. In the next step, each onlooker bee will choose a food source depending on its quality. With the Pareto-based methods, the relationships between the solutions are expressed by dominated or not[14]. First, the nondominated individuals in the whole population are selected as the first rank solutions and its rank is set as one. Next, the nondominated individuals among the remaining are selected as the second rank solutions and its rank is set as two and so on, until the population is zero. In the PMABCA, the quality of a food source is expressed by the fitness value; all the bees are sorted based on their nondominated rank and the preference distance. The fitness value of thei-th food source is calculated by using the following equation: (7) wherern,ianddp,irepresent the nondominated rank and the preference distance of thei-th food source, respectively. 3.1.4 Onlooker bees optimization At this stage, each onlooker selects a food source based on the fitness value calculated before. After the food source is selected, each onlooker bee will perform the same local search approaches and greedy selection procedure as the employed bees. In the PMABCA, based on the fitness value calculated before, the probability for each food source advertised by the corresponding employed bee will be calculated as follows[7]: (8) whereTs(·) is the selection function. 3.1.5 Scouts optimization If a food source cannot be further improved through a limit cycle, then the food source is assumed to be abandoned and the corresponding bee will become a scout[7]. Then the scout conducts a random search, and generates a new food source following the initialization of the population. 3.1.6 Archive updating and preference upper limit renewal In the first run, nondominated solutions are added to the archive directly. After that, in the end of each iteration, the new generated nondominated solutions are compared to the solutions in the archive.The candidate solutions that are not dominated by the solutions of the archive are added to it. Then, the dominated solutions are removed from the archive. As the capacity of the archive is finite, if the archive is full of nondominated solutions, it is necessary to remove the extra ones. In the PMABCA, many preference solutions and a few other solutions are kept in the same archive. Hence, the traditional diversity maintenance strategy to keep the uniformity is not appropriate. In this paper, an improved CD operator is applied to remove the extra ones. The CD is first addressed by Deb[14]for keeping a uniformly spread-out of thePF. The CD value of thei-th individual is calculated as follows: and (9) In the PMABCA, the CD is improved and uses the following equation: (10) whereβis the upper limit for preference, andλis the coefficient for the preference solutions. The value ofλis set to be 4 after a large number of experiments. If more preference solutions are preferred, the value ofλcan be set to be greater than 4. In addition, the value ofβis set adaptively according to the medial value of the preference distance in the former archive. To be more specific,βis equal to thek-th value of the ascending sequence according to the preference value in each iteration, wherekis set to be 0.6na, andnais the size of the archive. 3.1.7 Extra solutions removal in the archive In order to obtain a good distribution ofPF, the method proposed in Ref.[15] is adopted to remove the extra solutions. The extra ones with the smallest CD values are removed one by one, and the CD values for the remaining members of the set are updated after each removal. 3.2 Verification and comparison of PMABCA In this section, the computational results obtained by the PMABCA is compared to the NSGAII[14]and the PMABCA_D, respectively. The running mechanism of the PMABCA_D is the same as that of the PMABCA. The only difference between them is a different preference expression method. Specifically, the PMABC_D adopts the weighted Euclidean distance measure addressed by Deb. The selected two test functionsP1andP2are given as follows[14,16]: (11) (12) The experiments are executed in a PC using Matlab, and the clock speed of the PC is 2.6 GHz. The population size and archive size of the three algorithms are all set to be 100 and 50, respectively. In order to compare the running time of these algorithms better, the iteration cycle is set to be 1 000. In the experiments, we performed 30 independent runs on each test problem. What is listed in Tab.1 is the average CPU execution time of the 30 runs. Tab.1 Running time of the three algorithms s It is clear that the PMABCA_D is the fastest, the PMABCA is slightly slower, and the NSGAII is the slowest. The PMABCA is somewhat slower than the PMABCA_D, which is mainly due to the new proposed preference distance calculation operator. The longest running time of the NSGAⅡ is most likely deduced by the mating selection operator, moreover, there are more individuals to be compared during the searching process. Fig.2 and Fig.3 are the comparisons of the experimental results. In problem P1, the reference point is set to be (0.5,1), and the coefficients are set to be (0.5,0.5). As for the problem P2, the reference point is set to be (3,4,3), and the coefficients are set to be (0.5,0.25,0.25). (a) (b) (c) (a) (b) (c) As shown in Fig.2 and Fig.3, both the PMABCA and the PMABCA_D converge on thePF, and there are more preference solutions than non-preference solutions. Comparing thePFof PMABCA to that of PMABCA_D, it is clear that the preference area in the PMABCA is more compact. 4.1 PID controller of superheated steam temperature control system A simplified block diagram of the superheated steam temperature cascade control system which uses spray water injection as the deputy controller is shown in Fig.4[17]. The spray water injection control system, which is extracted to quickly respond, serves as a deputy controller; the superheated outlet steam temperature, which is characterized by hysteresis and nonlinearity, serves as the primary controller. In Fig.4,ris the set point of superheated steam temperature;Tais the intermediate steam temperature;Tis the superheated steam temperature;Wal(s) andWa2(s) are the deputy and the primary controller, respectively;Wol(s) andWo2(s) are the corresponding transfer func-tions, mA/℃;WHl(s) andWH2(s) are the corresponding measurement units. The transfer functions of the intermediate and superheated steam temperatures are shown as follows[18]: Fig.4 The boil superheated steam temperature cascade control system (13) (14) Since the deputy controller only approximately regulates the intermediate steam temperature, a fixed proportional controller is usually used in order to simplify the design of the controller,Wa1(s)=Kp1. The primary controller is employed to regulate the steam temperature to its set point precisely, and it is designed to be a PID controller,Wa2(s)=Kp2+Ki2/s+Kd2s. The deputy controller and the primary controller of the cascade control system can be adjusted respectively. The purpose of this paper is to search for the design parameters of the primary controller by the PMABCA. 4.2 Principle of multiobjective PID parameter optimization In this paper, we adoptts,σ,ψand ITAE as the objectives of the primary controller optimization in the superheated steam temperature cascade control system. In order to decrease the relativity of the objectives and increase the influence of the steady-state error, the ITAE is redefined as (15) wheretsmeans the settling time with an error bound of 5%. The definition of the ITAE is changed, only considering the errors after the settling time. Since before thets, the ITAE is relative toσandψ. With Eq.(15), the relationships amongσ,ψand ITAE are weakened. With the multiobjective optimization model, the PID parameter optimization is described as min (ts, 100-ψ,σ, ITAE′) s.t.Kpmin≤Kp≤Kpmax,Kimin≤Ki≤Kimax,Kdmin≤Kd≤Kdmax (16) 4.3 Simulation results Since predicting the ITAE value is somewhat difficult, the DM cannot properly express the preference for it. Whereas it is relatively simple to express preference via the parametersts,σandψ. Here the reference point is set to be 130, 10%, 95%, and there are no bias among all the objectives; i.e., the coefficients are set to be 1/3,1/3,1/3. The bound values ofKp,KiandKdare set according to Ref.[18], which are 2≤Kp≤4.5, 0.035≤Ki≤0.11, 30≤Kd≤45. The PID parameters are tuned based on the step response experiment. With the PMABCA, plenty of Pareto optimal solutions are achieved. Due to the limited space, only five groups of parameters are listed in Tab.2. Step responses curves of the first two selected groups of parameters are shown in Fig.5 with solid lines. As for comparison, the step responses curves of the top two groups parameters proposed in Ref.[17] are also shown in Fig.5 with dotted lines. It is clear that the simulation results of the PMABCA are more satisfactory than those of Ref.[17]. In addition, the preference distance values of each solution achieved by the PMABCA aid the DM in making a reasonable decision. Tab.2 Parameter and objective values of the selected ten groups Fig.5 Comparison of the step response curves A novel preference expression method is addressed, and a new preference-based multiobjective ABC algorithm is proposed. With the PMABCA, instead of the well covered and uniformly distributed set of Pareto optimal solutions, a preferred set of solutions and some other non-preference solutions are found simultaneously. Experimental results on the benchmark test problems validate its effectiveness. The preferences for different objectives can be expressed in the calculated solutions. Consequently, the PMABCA is used for the PID controller parameter tuning in the superheated steam temperature cascade control system of a boiler. Simulation results show that the DM’s preference can be easily addressed. A set of solutions which can meet the preference will aid the DM in making a reasonable decision. [1]Sanchez-Lopez A, Arroyo-Figueroa G, Villavicencio-Ramirez A. Advanced control algorithms for steam temperature regulation of thermal power plants[J].InternationalJournalofElectricalPower&EnergySystems, 2004, 26(10): 779-785. [2]Zhang J H, Zhang F F, Ren M F, et al. Cascade control of superheated steam temperature with neuro-PID controller[J].ISATransactions, 2012, 51(6): 778-785. [3]Riggs J B, Curtner K, Foslien W. Comparison of two advanced steam temperature controllers for coal-fired boilers[J].Computers&ChemicalEngineering, 1995, 19(5): 541-550. [4]Naidu K, Mokhlis H, Bakar A H A. Multiobjective optimization using weighted sum Artificial Bee Colony algorithm for Load Frequency Control[J].InternationalJournalofElectricalPower&EnergySystems, 2014, 55: 657-667. [5]Hung M H, Shu A S, Ho S J, et al. A novel intelligent multiobjective simulated annealing algorithm for designing robust PID controllers[J].IEEETransactionsonSystems,Man,andCybernetics,PartA:SystemsandHumans, 2008, 38(2): 319-330. [6]Pedersen G K M, Yang Z. Multi-objective PID-controller tuning for a magnetic levitation system using NSGA-Ⅱ[C]//Proceedingsofthe8thAnnualConferenceonGeneticandEvolutionaryComputation. Seattle, USA, 2006: 1737-1744. [7]Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri, Turkey: Computer Engineering Department, Erciyes University, 2005. [8]Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm [J].AppliedSoftComputing, 2008, 8(1): 687-697. [9]Zhou X, Shen J, Sheng J X. An immune recognition based algorithm for finding non-dominated set in multi-objective optimization[C]//Pacific-AsiaWorkshoponComputationalIntelligenceandIndustrialApplication. Wuhan, China, 2008: 305-310. [10]Branke J, Deb K. Integrating user preferences into evolutionary multi-objective optimization[M]//KnowledgeIncorporationinEvolutionaryComputation. Berlin: Springer, 2005: 461-477. [11]Coello C A C. Handling preferences in evolutionary multiobjective optimization: a survey[C]//Proceedingsofthe2000CongressonEvolutionaryComputation. La Jolla, CA, USA, 2000, 1: 30-37. [12]Molina J, Santana L V, Hernández-Díaz A G, et al. g-dominance:Reference point based dominance for multiobjective metaheuristics[J].EuropeanJournalofOperationalResearch, 2009, 197(2): 685-692. [13]Deb K, Sundar J, Udaya Bhaskara Rao N, et al. Reference point based multi-objective optimization using evolutionary algorithms[J].InternationalJournalofComputationalIntelligenceResearch, 2006, 2(3): 273-286. [14]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J].TransactionsonEvolutionaryComputation, 2002, 6(2): 182-197. [15]Luo B, Zheng J, Xie J, et al. Dynamic crowding distance? A new diversity maintenance strategy for MOEAs[C]//ProceedingsoftheFourthInternationalConferenceonNaturalComputation. Jinan, China, 2008: 580-585. [16]Zitzler E, Laumanns M, Thiele L. Spea2: improving the strength Pareto evolutionary algorithm [R]. Zurich, Switzerland: Computer Engineering and Networks Laboratory(TIK), ETH Zurich, 2001. [17]Zhao L, Ju G, Lu J. An improved genetic algorithm in multi-objective optimization and its application[J].ProceedingsoftheCSEE, 2008, 28(2): 96-102. (in Chinese) [18]Li M, Shen J. Simulating study of adaptive GA-based PID parameter optimization for the control of superheated steam temperature[J].ProceedingsoftheCSEE, 2002, 22(8): 145-149. (in Chinese) 基于偏好多目标蜂群算法的过热汽温控制系统优化 周 霞1,2沈 炯1李益国1 (1东南大学能源与环境学院, 南京 210096)(2金陵科技学院机电工程学院, 南京 211169) 为了将决策者的偏好综合到多目标问题求解过程中,提出了一种偏好多目标蜂群优化算法PMABCA.在PMABCA中,给出了一种新的偏好距离计算方法,基于非支配等级与偏好距离定义了适应度分配函数,并引入了归档集用于非支配解的存储.为了清除非支配集中多余的解,提出了改进的偏好拥挤距离算子.针对经典函数优化问题的计算结果表明,PMABCA可以在输出完整Pareto前端的基础上,确保输出大量符合偏好的最优解.将PMABCA应用于过热汽温控制系统PID参数优化问题,仿真结果表明,新算法的结果更便于决策者做出合理决策. 偏好;多目标;蜂群;过热汽温控制;优化 TK39; TP391 Received 2014-06-26. Biographies:Zhou Xia (1976—), female, doctor, lecturer, zenia77@163.com; Shen Jiong (corresponding author), male, doctor, professor, shenj@seu.edu.cn. The National Natural Science Foundation of China (No.51306082, 51476027). :Zhou Xia, Shen Jiong, Li Yiguo. Preference-based multiobjective artificial bee colony algorithm for optimization of superheated steam temperature control[J].Journal of Southeast University (English Edition),2014,30(4):449-455. 10.3969/j.issn.1003-7985.2014.04.009 10.3969/j.issn.1003-7985.2014.04.0092 A Novel Preference Expression Method
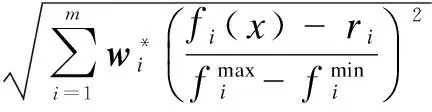
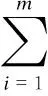


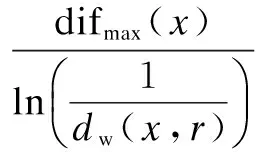

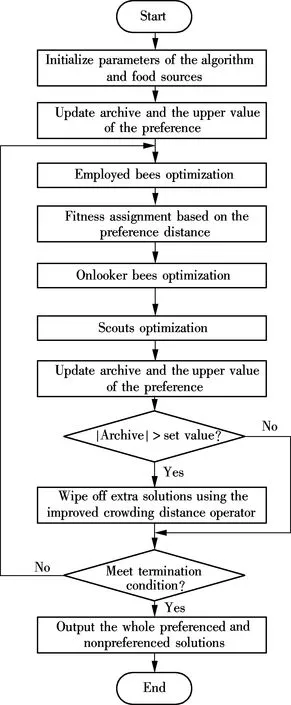
3 Proposed PMABCA
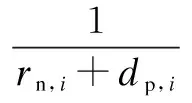

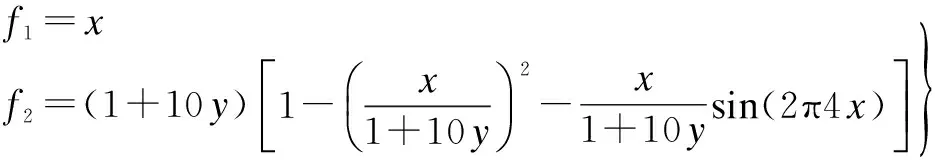


4 Optimization of Superheated Steam Temperature Control

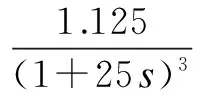

5 Conclusion
 Journal of Southeast University(English Edition)2014年4期
Journal of Southeast University(English Edition)2014年4期
