页岩可压性指数评价新方法及应用
蒋廷学, 卞晓冰, 苏 瑗, 刘双莲, 卫 然
(中国石化石油工程技术研究院,北京 100101)
页岩裂缝的起裂与扩展是压裂的核心问题,与钻井中岩石的可钻性相类似,页岩压裂也存在岩石的可压性问题。国外的页岩可压性研究主要集中在页岩脆性指数的研究上:R.J.Evans在1990年给出了页岩脆性的定义[1];J.D.Ingram在1992年提出用过度胶结和正常胶结岩石的单轴抗压强度比值来表征脆性指数[2];D.Jarvie在2008年提出用脆性矿物占总矿物组分的比例来表征脆性指数[3];此后,其他学者从岩石力学的角度来表征脆性指数[4-7]。但上述研究都是从室内岩心分析或测井的方法出发,反映的仅是近井筒的情况,且获取的岩心不一定具有代表性;测井信息反映的是动态值,难以反映压裂的准静态过程。开发中后期的岩心及水平段测井资料都很少,唯一可供借鉴的就是大量的压裂施工资料。鉴于此,笔者提出了基于压裂施工压力曲线求取页岩脆性指数的新方法,建立了综合性的可压性指数评价新模型;同时,考虑页岩水平井分段压裂的特殊性,即每段裂缝起裂处的岩石可压性指数也不尽相同,建立了利用每段压裂施工数据(压裂液总量及支撑剂总量)表征页岩可压性指数的评价模型。
1 页岩脆性指数
李庆辉等人[8]总结了国外计算脆性指数的20种方法[9-14],这些方法分别从岩石的强度、硬度及应力应变特征等方面表征脆性指数,虽有一定的指导性,但局限性也非常明显,各方法仅从某个角度进行分析,在同样的地层条件下计算的结果也差别很大。以彭水地区为例,按现有方法计算的页岩脆性指数最小为40.1%,最大为87.7%,无论取哪个值都缺乏说服力。为了充分考虑各因素的综合影响,研究了利用压裂施工时的破裂压力资料来求取脆性指数的新方法。
压裂实践表明,页岩的破裂压力与页岩的脆性指数息息相关[15-16]。页岩的脆性指数好,在升排量压裂过程中,即使很小的排量地层也会出现破裂,达到设计排量时还会出现多次破裂现象;反之,如果页岩的塑性特征强,达到设计排量时也难以出现明显的破裂特征。
可从能量的角度来表述页岩的脆性与塑性特征。强塑性页岩地层破裂后压力几乎不变,但变形一直持续存在,此时消耗的能量是最大的,消耗的能量可简化为变形长度与变形期间基本恒定压力的乘积,用水力压裂施工参数来表示,可等效为施工压力(井口压力必须转换为井底压力)、施工排量及施工时间的乘积。考虑到在此变形期间,压力、排量等可能一直是变化的,必须采用地层破裂期间内井底施工压力与排量的乘积,并对时间进行积分来求得。为简化起见,假设地层破裂变形期间的排量是恒定的。
同样,脆性强的页层地层破裂后,压力快速下降。显然,此时消耗的能量就相对较小。
脆性地层与塑性地层消耗的能量不同。完全塑性页岩地层破裂后,压力一直处于峰值且恒定不变,形变匀速增加,此时消耗的能量最大,以此为基数,其脆性指数为0;而完全脆性页岩地层破裂后,压力应呈直线式下降,即压力快速降至最低值,其脆性指数为1.0。
完全塑性页岩及完全脆性页岩是2个临界极值点,大部分情况下的脆性指数介于两者之间,此时脆性指数的表达式为:
(1)
式中:IB为页岩的脆性指数;Ep为完全塑性页岩破裂后消耗的能量,J;Eb为完全脆性页岩破裂后消耗的能量,J。
水力压裂施工时,上述能量可转变为井底施工压力与排量的乘积,并对时间进行积分,则:

(2)
按上述假设,破裂变形期间的排量保持恒定,则式(2)中与排量有关的井筒摩阻pf也是恒量,式(2)可转变为:

(3)
式中:E为压裂消耗的能量,J;Q为压裂施工排量,m3/min;p(t)为井口施工压力,MPa;ph为静液柱压力,MPa;pf为井筒摩阻压力,MPa;tc为地层破裂变形后压力下降至最低值时的时间,min;t0为地层变形后压力上升至最高值时的时间,min。
将式(3)代入式(1),并考虑塑性与脆性的不同特性,得:
(4)
式中,pmax为页岩塑性形变过程中井口压力升至的最高值,MPa。
为直观起见,可用图形表示脆性指数覆盖的能量区域面积(见图1)。

图1 压裂施工曲线中塑性与脆性覆盖的能量区域示意Fig.1 Sketch map of energy zone controlled by plasticity and brittleness in fracturing operation
出现多次破裂的情况时,每次破裂情况都可按上述方法进行处理,但因每次压裂施工排量不同,脆性覆盖的能量区域的比例也不同,不能将各次得出的脆性指数进行简单的算术平均,理想的处理方法是将各次的脆性覆盖的能量区域面积求和,再与塑性覆盖的能量区域面积之和相除,最终得出的脆性指数能够综合反映施工排量的权重因素。为直观起见,多次破裂的脆性指数求取方法如图2所示。
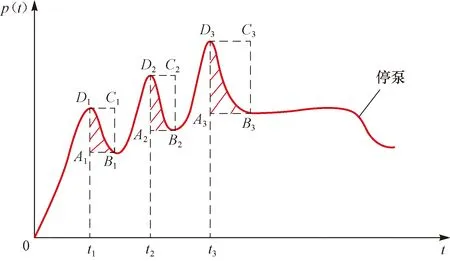
图2 压裂施工曲线中多次破裂时塑性与脆性覆盖的能量区域示意Fig.2 Sketch map of energy zone controlled by plasticity and brittleness in multistage fracturing
按上述方法求取的页岩脆性指数涵盖了以往方法考虑的页岩硬度、强度及岩石力学特性等参数,在这些参数的综合作用下,在宏观上反映了压裂时的岩石变形及破裂特征。
彭水地区页岩按基于页岩破裂压力特征表征脆性指数方法计算的脆性指数为54.8%,与现有方法计算的结果有所不同,但该结果考虑了各因素在力学宏观上的综合作用效果,更符合实际情况。
2 页岩可压性指数
2.1 基于脆性指数及地质甜点指标的页岩可压性指数评价方法
脆性指数只是可压性指数的一个方面,实际上,可压性指数还应考虑地质甜点的因素。也就是说,最终的可压性指数大小,不但要反映页岩本身的脆性(可压裂性),还要反映压裂后出气的潜力,这样的可压性指标才能作为段簇位置优选的依据,也更具有现实的指导作用。
考虑脆性指数及地质甜点指标的可压性指数模型为:
(5)
式中:If为页岩可压性指数;S1,S2分别为影响可压性指数的因素1及因素2,此处指脆性指数及地质甜点指数;w1,w2分别为S1,S2的权重因子。
权重因子的确定一般采用层次分析法,也可根据需要由专家评判确定,只要2个权重因子之和为1.0即可。
地质甜点是一个综合性的指标,包括热成熟度、含气丰度、吸附气饱和度或其他影响含气性的相关指标,只要满足相互独立性即可。地质甜点指数的求取方法与式(5)类似,在此不赘述。
2.2 基于压裂施工参数的页岩可压性指数评价方法
基于脆性指数及地质甜点指标的页岩可压性指数,虽然考虑的因素比较多,但仅考虑了近井筒的特性参数(包括前期的破裂压力特性,也属近井筒范畴;其他的地质甜点指标如测井和岩心分析的数据,同样是近井筒参数)。因此,该可压性指标不能反映远井的地层可压性情况。远井的地质甜点指标难以准确获取,但可以通过压裂施工参数将远井页岩本身的可压性特征反演出来。基于此,提出了利用压裂施工参数(如加砂量及压裂液量等参数)来表征远井地层可压性指数的新方法。
压裂施工中泵入地层的所有压裂液,不论是前置液、携砂液,还是段塞式加砂时的中顶液,目的都是造缝和防止砂堵,最终目的都是多加砂;同样地,压裂时泵入的所有支撑剂量反映了地层能否接纳的最大支撑剂量。该支撑剂量与泵入地层的所有压裂液量的比值大小,就反映了页岩地层压裂的难易程度。该比值越高,远井的地层可压性越好,反之越差。
由于进入地层的压裂液类型及黏度都不同,常用的有滑溜水、低黏胶液及中黏胶液,因此,将进入地层的压裂液总量采用等效的方法折算为滑溜水,此时的低黏胶液及中黏胶液的量就应当按砂液比的高低进行折算,如中黏胶液的砂液比是滑溜水的2倍,则其换算为滑溜水时也应将原中黏胶液体积乘以2,其计算公式为:
(6)
式中:Vf′为胶液折算体积,m3;Vf为胶液体积,m3;Rl为胶液砂液比;Rs为滑溜水砂液比。
同样地,因为支撑剂的类型及粒径不同,为简便起见,仅考虑支撑剂的粒径不同,由于一般采用40/70目支撑剂为主体支撑剂,为统一对比,需将100目的支撑剂和30/50目的支撑剂,折算为40/70目的支撑剂。折算方法是按平均粒径的比例进行计算,只是100目支撑剂折算后按对应比例缩小,而30/50目支撑剂折算后按对应的比例增大。其计算公式为:
(7)

需要指出的是,按上述方法算出来的数值可能太小,需进行归一化处理:
(8)

对压裂液量及支撑剂量都与区块的最大和最小用量为参照进行归一化处理,这样计算的可压性指数为0~1。
3 现场应用及效果分析
涪陵焦石坝区块的主要目的层位是上奥陶统五峰组—下志留统龙马溪组下部页岩气层,埋深2 330.00~2 415.00 m,为一套黑色粉砂质页岩及灰黑色碳质页岩。页岩基本参数总有机碳含量为3.51%,镜质体反射率为2.42,硅质含量为30%~58%,黏土矿物含量为15%~30%,孔隙度为4.61%,渗透率为0.032 3 mD,区块含气性为4.63 m3/t(其中吸附气占54%),页岩弹性模量为38.0 GPa,泊松比为0.198。
涪陵焦石坝区块的2口水平井A井和B井皆位于焦石坝构造高部位,具有较好的可对比性。2口井都进行了15段压裂施工,基本参数见表1,典型施工曲线见图3。

表1 焦石坝区块2口页岩气井的施工参数Table 1 Basic parameters of 2 shale gas wells in Jiaoshiba Block
在此基础上,应用新方法计算了2口井的页岩脆性指数及综合可压性指数,结果见表2。其中,If1为考虑脆性指数及地质甜点指标的可压性指数计算结果,If2为基于压裂施工参数的可压性指数计算结果。由表2可以看出,新方法计算的脆性指数和可压性指数越高,对应气井的无阻流量也越大,这表明新方法合理。以前常规方法仅考虑了近井筒参数,且不同方法的计算结果差异较大,与压后效果的关联度不高。

图3 焦石坝区块2口页岩气井典型施工曲线Fig.3 Typical treatment curves of 2 shale gas wells in Jiaoshiba Block
表2焦石坝区块2口页岩气井可压性指数及无阻流量对比
Table2Fracabilityindexandopenflowcapacityof2shalegaswellsinJiaoshibaBlock
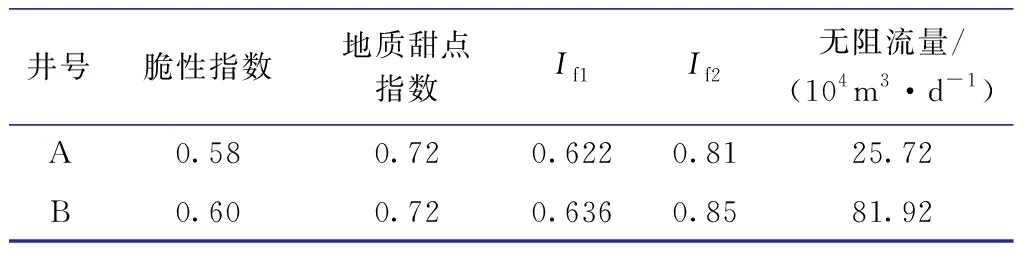
井号脆性指数地质甜点指数If1If2无阻流量/(104m3·d-1)A0.580.720.6220.8125.72B0.600.720.6360.8581.92
4 结论与建议
1) 在国外常规脆性指数评价方法的基础上,提出了利用压裂施工中的能量区域面积表征脆性指数的新方法。
2) 基于脆性指数新方法及地质甜点指数,同时考虑各参数的权重分配,提出了考虑页岩脆性及出气潜力的可压性指数新模型,其计算结果可作为页岩水平井分段压裂段簇位置选择的依据。
3) 基于压裂施工参数,提出了应用归一化等效支撑剂量与归一化等效压裂液量的比值大小表征可压性指数的新思路,用以表征页岩远井的可压性。
4) 现场几口井的计算结果表明,压后产气效果与计算的脆性指数及可压性指数关联度较强,而与以往方法的计算结果关联度不高,表明新方法现场可操作性。
5) 建议在焦石坝等页岩气主要区块开展新方法的适应性评价和后续推广应用,以达到页岩气开发降本增效的目的。
参考文献
References
[1] Evans R J,Klein J D,Walls J D,et al.Part Iii:the mechanics of electrical resistivity measurement on rock samples;SCA guidelines for sample preparation and porosity measurement of electrical resistivity samples[J].The Log Analyst,1990,31(2):64-67.
[2] Ingram J D.Research in ’90s[R].SEG 1992-1396,1992.
[3] Jarvie D.Finding bypassed or overlooked pay zones using geochemistry techniques[R].IPTC 12918,2008.
[4] Wang F P,Reed R M.Pore networks and fluid flow in gas shales[R].SPE 124253,2009.
[5] Rickman R,Mullen M,Petre E,et al.A practical use of shale petrophysics for stimulation design optimization:all shale playsare not clones of the Barnett Shale[R].SPE 115258,2008.
[6] 杨建,付永强,陈鸿飞,等.页岩储层的岩石力学特征[J].天然气工业,2012,32(7):12-14.
Yang Jian,Fu Yongqiang,Chen Hongfei,et al.Rock mechanical characteristics of shale reservoirs[J].Natural Gas Industry,2012,32(7):12-14.
[7] 张艺耀,王世彬,郭建春.页岩地层压裂工艺新进展[J].断块油气田,2013,20(3):278-281.
Zhang Yiyao,Wang Shibin,Guo Jianchun.New progress of hydraulic fracturing technology for shale formation[J].Fault-
Block Oil & Gas Field,2013,20(3):278-281.
[8] 李庆辉,陈勉,金衍,等.页岩脆性的室内评价方法及改进[J].岩石力学与工程学报,2012,31(8):1680-1685.
Li Qinghui,Chen Mian,Jin Yan,et al.Indoor evaluation method for shale brittleness and improvement[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(8):1680-1685.
[9] Heteny M.Handbook of experimental stress analysis[M].New York:John Wiley,1966:23-25.
[10] Lawn B R,Marshall D B.Hardness,toughness and brittleness:an indentation analysis[J].Journal of American Ceramic Society,1979,62(7):347-350.
[11] Jesse V H.Glossary of geology and related sciences[M].Washington: American Geological Institute,1960:99-102.
[12] Quinn J B,Quinn G D.Indentation brittleness of ceramics: a fresh approach[J].Journal of Materials Science,1997,32(16):4331-4346.
[13] Griggs David,Handin John.Rock deformation: a symposium[M].New York:Waverly Press,1960:66-67.
[14] Bishop A W.Progressive failure with special reference to the mechanism causing it[C]∥Proceedings of the Geotechnical Conference,Olso:[s.n.],1967:142-150.
[15] 赵海峰,陈勉,金衍.页岩气藏网状裂缝系统的演示断裂动力学[J].石油勘探与开发,2012,39(4):464-470.
Zhao Haifeng,Chen Mian,Jin Yan.Rock fracture kinetics of the fracture mesh system in shale gas reservoirs[J].Petroleum Exploration and Development, 2012,39(4):464-470.
[16] 尹虎,王新海,张芳,等.吸附气对气水两相流页岩气井井底压力的影响[J].断块油气田,2013,20(1):74-76.
Yin Hu,Wang Xinhai,Zhang Fang,et al.Influence of adsorbed gas on bottomhole pressure of shale gas wells with gas-water two-phase flow[J].Fault-Block Oil & Gas Field,2013,20(1):74-76.

