基于近似投影校正的无线传感器网络三维定位机制*
胡中栋,谢金伟
(江西理工大学信息工程学院,江西 赣州 341000)
基于近似投影校正的无线传感器网络三维定位机制*
胡中栋*,谢金伟
(江西理工大学信息工程学院,江西 赣州 341000)
针对三维DV-Hop无线传感器定位算法存在定位误差较大的问题,提出了近似投影校正的无线传感器网络非测距三维定位算法。充分利用已有的地形特点,将经典的三维DV-Hop算法所求得的结果进行近似投影,尽可能投影到离地形表明较近的地方,大幅度减小了定位误差。用二维高斯分布密度函数模拟山头地形的场景中,相对定位误差为35%左右,较大幅度提高了定位精度,有较高的实用价值。
无线传感器网络;三维DV-Hop;山头地形;近似投影
随着万物互联的理念不断深入人心,采集信息就成了许多领域的重要工作。而就目前而言,带有GPS功能的无线传感器因其价格太高无法大范围部署,因此无线传感器网络中大部分传感器节点都不具有定位功能。无法定位的传感器很多情况下不能承担采集需求信息的任务,所采集的信息不具有实际意义[1],因此定位就成了无线传感器网络领域的研究热点,且定位信息对路由也起着重要的作用[2]。有许多不同的定位算法,APIT(Approximate Point In Triangle)[3]算法是一种不基于其它测量设备的自定位算法,文献[4]将其应用扩展到了三维;陈岁生[5]等人利用MDS-MAP和非线性滤波的方法设计了WSN定位算法;黄亮[6]等人根据距离重构原理提高了定位精度;程秀芝[7]等人利用RSSI对传统定位方法进行校正;张亚明[8]等人对不对称链路环境下WSN定位算法进行了研究;江禹生[9]等通过加权质心算法对未知节点进行定位。
基于近似投影校正的无线传感器网络三维定位:因山头不能抽象成具体的函数模型,很难直接进行投影,本文提出了近似投影校正的方法。在三维DV-Hop定位算法求解结果的基础上进行近似投影修正以提高定位精度。假设三维DV-Hop求解的结果为P,首先将P点沿x,y,z坐标轴投影到山头地形表面,得到三个新的点P1,P2,P3。求出过P1,P2,P3三个点的平面,将P点投影到该平面上,得到投影点P′,用P′代替P。该方法能够修正未知节点的位置,较大幅度的提高传感器节点的定位精度。
1 三维DV-Hop算法
1.1 DV-Hop算法
Niculescu D等人利用距离矢量路由的原理提出DV-Hop算法[10]。本文暂未考虑无法求解的孤立点等特殊情况。通过广播在所有节点间进行信息交换,得到每一个节点到其它节点的最小跳数信息。每一个锚节点都根据自身的位置及与其它所有锚节点之间的最小跳数计算出平均每跳距离。根据未知节点i到锚节点j的最小跳数,再用到未知节点i最近锚节点的平均跳距估算出未知节点i到锚节点j的距离。
根据以上信息通过最小二乘法(极大似然估计法)计算自身坐标[11]。若未知节点的坐标为(x,y,z),已求出该未知节点到锚节点(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn)的距离分别为d1,d2,…dn(n≥4)。可得矛盾方程组:
AX=B
(1)
其中:
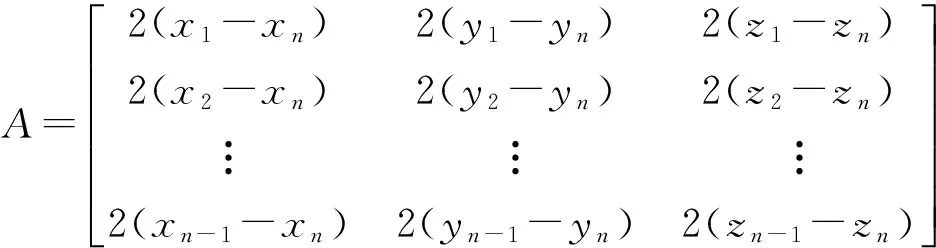
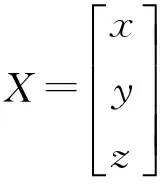
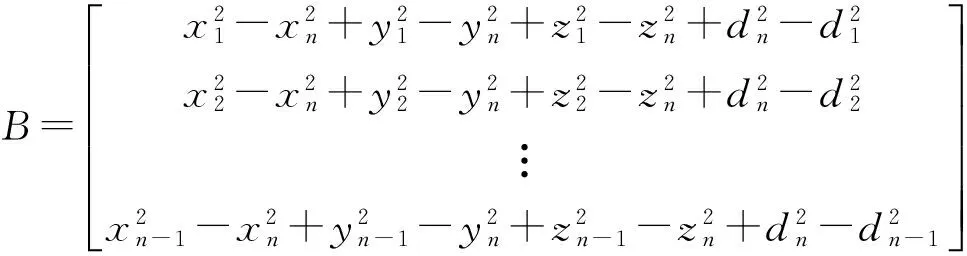
若矛盾方程组有解则可得:
X=(ATA)-1ATB
(2)
1.2 性能评价
一般用相对定位误差来评价算法的性能[12]。
若某个未知节点的估算坐标(xi,yi,zi)和实际坐标(ai,bi,ci)的差距Δdi为:
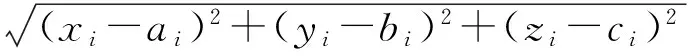
(3)
则n个未知节点的平均定位误差Δ可表示为:
(4)
2 近似投影校正的三维定位算法
用二维高斯分布的密度函数来模拟山头地形比规则函数更具有一般性,能够较好的证明算法的优越性。设二维高斯分布的密度函数为:
(5)
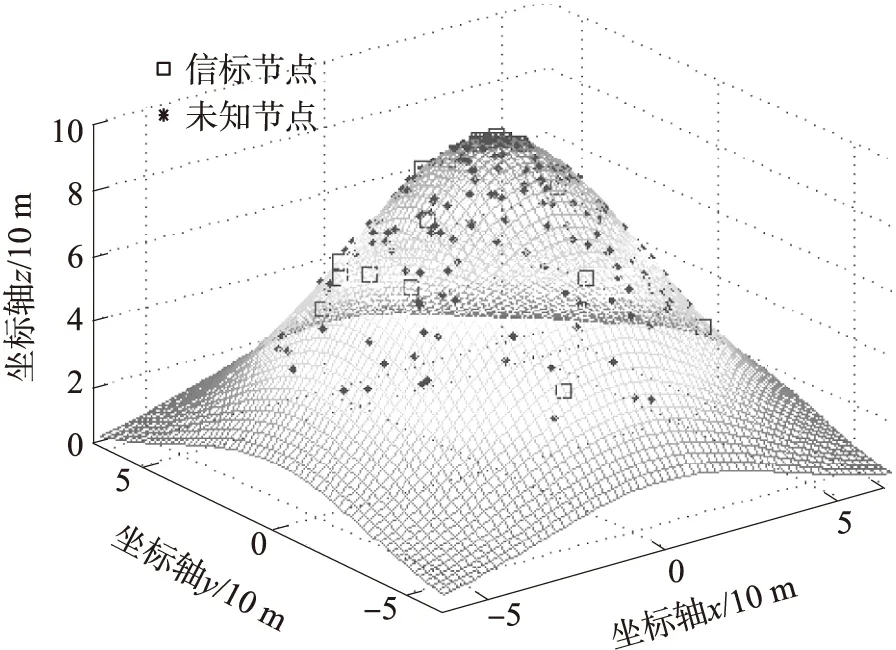
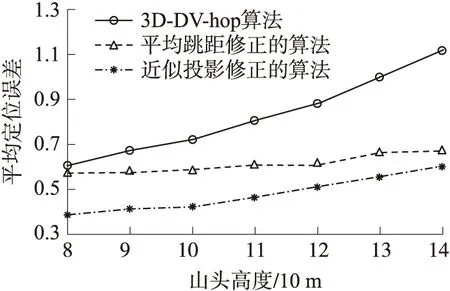
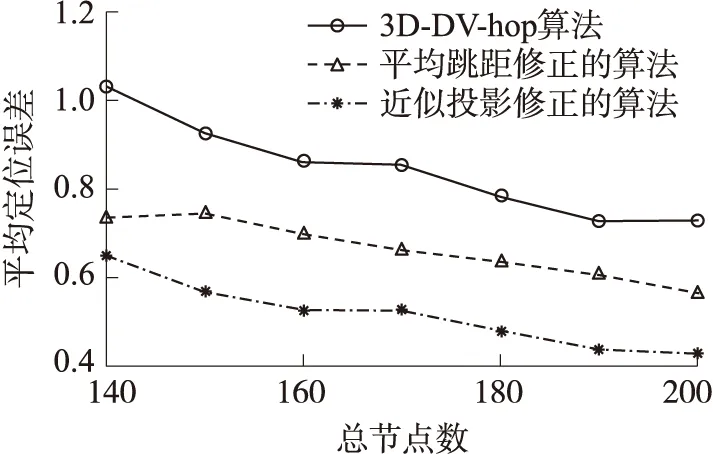
作过点(0,0,L)且平行于xoy的平面,其中0 近似投影校正的具体方法如图1所示,设三维DV-Hop求解的结果为P,首先将P点沿x坐标向山头表面投影得到P1点,然后将P沿y坐标轴进行投影得到P2点,最后将P沿z坐标轴进行投影得到P3点。过P1,P2,P3三个点作平面,然后将P点垂直投影到该平面上,投影点为P′,P′即为P修正后的解。在上述投影过程中,有可能存在偏离山头无法投影的特殊点,下文将进行具体说明。 设经典三维DV-Hop算法所求得的解P对应的坐标为(a,b,c),沿x,y,z坐标轴投影得到的三个点为P1,P2,P3,对应的坐标为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)。 首先消除过高和过低点,在式(5)模拟的山头中不可能有比山高的点,也不可能有比山低的点,但是经典三维DV-Hop算法可能求出越界的点。假设P(a,b,c)点的c大于上界H,则将P更新为(a,b,H-0.001),若c小于下限L,则将P更新为(a,b,L+0.001),因在山顶和山底无法投影,所以需要小幅修正。 将式(5)解出x,y可得: (6) (7) 根据式(5)~式(7)可求得P点沿x,y,z坐标轴线投影所得的点,即过P点且与坐标轴平行的直线与山体表面的交点。正常情况下可得两个交点,取与P点坐标分量值符号相同的交点,如P点坐标(a,b,c)中若a>0则取两个交点中x坐标值为正的交点,否则取x坐标值为负的交点。也可能发生无法投影的情况,具体过程如下: 情况1:若-ln(c/H)-(b/5)2≥0与-ln(c/H)-(a/5)2≥0均成立,则说明P沿x,y坐标轴线可以投影,投影后得到的投影点P1,P2,P3为: 情况2:若-ln(c/H)-(b/5)2<0与-ln(c/H)-(a/5)2≥0均成立,则表明沿x坐标轴线无法投影,一般为x值接近0的情况。将沿x坐标轴线的投影修正为先将P点改为(0,b,c),然后再沿y坐标轴线投影,投影后得到的投影点P1为: 沿y,z坐标轴线的投影结果与情况1相同。 情况3:若-ln(c/H)-(b/5)2≥0与-ln(c/H)-(a/5)2<0均成立,则表明沿y坐标轴线无法投影,一般为y值接近0的情况。将沿y坐标轴线的投影修正为先将P点改为(a,0,c),然后再沿x坐标轴线投影,投影后得到的投影点P2为: 沿x,z坐标轴线的投影结果与情况1相同。 情况4:若-ln(c/H)-(b/5)2<0与-ln(c/H)-(a/5)2<0均成立,则表明沿x,y坐标轴线均无法投影,分别进行情况2和情况3的操作得到P1,P2,当求P1时P更新为(0,b,c),当求P2时P更新为(a,0,c): 沿z坐标轴线的投影结果与情况1相同。 因进行了修正,P1,P2,P3必定不在一条直线上,可求得过P1,P2,P3三点的平面为: Ax+By+Cz+D=0 (8) 其中: A=y1z2-y1z3-y2z1+y2z3+y3z1-y3z2 P′点即为近似投影修正后的定位结果。 采用Matlab对本文设计的近似投影校正算法进行了仿真实验,实验用三种方法进行了对比实验,分别为经典的三维DV-Hop定位算法、基于平均跳距修正的三维DV-Hop定位算法和本文提出的近似投影校正算法。用式(5)模拟山头,以10 m为一个单位,其中L=H·e-1,实验分为山头高度不同、信标节点比例不同与节点总数不同3种情况进行。实验中节点的通信半径设置为20 m,其它参数根据不同的情况进行设置,节点随机分布的一个实例如图2所示。 3.1 不同山头高度的实验 实验中传感器节点总数设为200,信标节点占10%。式(5)中的H分别设为8、9、10、11、12、13、14进行实验,对每个不同的H值均进行100次实验,每次实验的传感器节点都是随机分布的,相对定位误差取100次实验结果的平均值,实验结果如图3所示,虽然随着山的高度不断增加,两种算法相对定位误差都在增加,但经近似投影的节点定位精度明显高于经典的三维DV-Hop定位算法与基于平均跳距修正的三维DV-Hop定位算法。 图2 传感器节点随机分布图 图3 不同山头高度的平均定位误差 3.2 不同锚点比例实验 实验中H的值设定为10,传感器节点总数设为200,信标节点的比例取5%、10%、15%、20%、25%、30%和35%进行实验,对每种不同比例分别进行100次模拟实验,每次实验的传感器节点分布都是随机的,相对定位误差取100次实验结果的平均值,实验结果如图4所示,当锚点比例超过20%时,在复杂的模拟环境下,近似投影算法的相对定位误差已经降低到40%以下,大幅度提高了算法的可用性。 图4 不同锚节点比例的平均定位误差 3.3 传感器节点数不同的实验 实验中H的值设定为10,锚节点比例固定为10%,实验中节点总数分别为140、150、160、170、180、190和200的情况下进行,对每组数据进行100次实验,每次实验时传感器节点分布都是随机的,相对定位误差取100次实验结果的平均值,实验结果如图5所示,结果显示如果合理部署传感器节点,基于近似投影的非测距三维定位算法的相对定位误差低于40%,较原有算法定位精度有较大幅度的提高。 图5 不同节点总数的平均定位误差 本文设计的基于近似投影的无线传感器网络三维定位算法有效的利用了外部环境的特点,用近似投影的方法有效的克服了不规则图形无法直接投影的缺陷。通过多角度的仿真对比实验证明,本文设计的算法在近似真实山头模型中表现良好,有效提高了无线传感器网络非测距定位算法精度,具有较高的实用价值。 [1] 谢亚琴,张业荣. 基于APIT和TSE算法的混合定位方法[J]. 南京邮电大学学报(自然科学版),2007,27(6):68-71. [2]Rao A,Ratnasamy S,Papadimitriou C,et al. Geographic Rollting without Location Information[C]//MobiCom. San Diego:ACM Press,2003:96-108. [3]He Tian,Huang Chengdu,Blum B M,et al. Range-Free Localization Schemes for Large Scale Sensor Networks[C]//MobiCom. San Diego:ACM Press,2003:81-95. [4]刘玉恒,蒲菊华,赫阳. 无线传感器网络三维自身定位方法[J]. 北京航天航空大学学报,2008,34(6):647-651. [5]陈岁生,卢建刚,楼晓春. 基于MDS-MAP和非线性滤波的WSN定位算法[J]. 浙江大学学报(工学版),2012,46(5):866-872. [6]黄亮,王福豹,段渭军,等. 基于距离重构的无线传感器网络多维定标定位算法[J]. 传感技术学报,2013,26(9):1284-1287. [7]程秀芝,朱达荣,张申,等. 基于RSSI差分校正的最小二乘—拟牛顿定位算法[J]. 传感技术学报,2014(1):123-127. [8]张亚明,史浩山,刘燕,等. 不对称链路环境下的WSN节点定位算法[J]. 传感技术学报,2014,27(3):320-326. [9]江禹生,冯砚毫,管芳,等. 无线传感网非测距三维节点定位算法[J]. 西安电子科技大学学报(自然科学版),2012,39(5):140-147. [10]Niculescu D,Nath B. DV-Based Positioning in Ad Hoc Networks[J]. Journal of Teleconununication Systems,2003,22(1-4):267-280. [11]严筱永,钱焕延,高德民,等. 一种基于多重共线性的三维DV-Hop定位算法[J]. 计算机科学,2011,38(5):37-40,44. [12]胡中栋,曾珽,肖红,等. 基于地形改正的无线传感器网络DV-Hop定位算法[J]. 传感器与微系统,2013,32(6):147-149. 胡中栋(1958-),男,汉族,江西婺源人,江西理工大学教授,硕士研究生导师,主要研究方向为无线传感器网络,智能计算,jxhzd@163.com; 谢金伟(1987-),男,汉族,江苏淮安人,江西理工大学硕士研究生,主要研究方向为无线传感器网络,智能计算。 The3DLocalizationMechanismforWirelessSensorNetworksBasedonApproximateProjectionCorrection* HUZhongdong*,XIEJinwei (School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China) This paper presents a non-dimensional distance wireless sensor network localization algorithm based on approximate projection correction for the problem that the localization error is large. The results which get by using the least squares method is approximate projected as close as possible to the surface of the mountain which full use of existing terrain features,greatly reducing the location error. In the two-dimensional Gaussian distribution density function simulation scenarios,the relative localization error is about 35%,dramatically increased the accuracy of location and it have high practical value. WSN;3D DV-Hop;mountain terrain;approximate projection 项目来源:江西省教育厅项目(GJJ10492);国家基金项目(61462034);江西省教育厅自然科学基金项目(GJJ13413) 2014-07-01修改日期:2014-09-16 10.3969/j.issn.1004-1699.2014.11.024 TP393 :A :1004-1699(2014)11-1573-05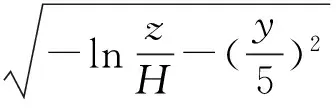
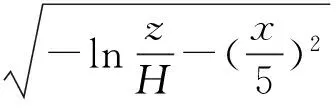
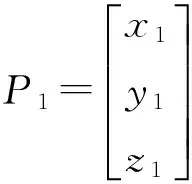
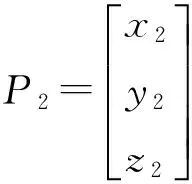
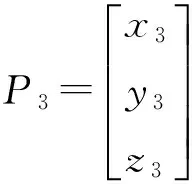
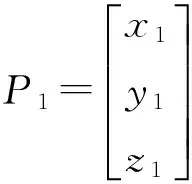
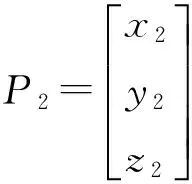
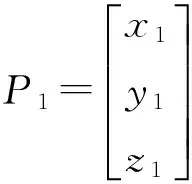
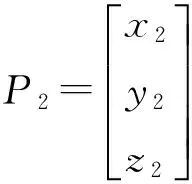
B=-x1z2+x1z3+x2z1-x2z3-x3z1+x3z2
C=x1y2-x1y3-x2y1+x2y3+x3y1-x3y2
D=-x1y2z3+x1y3z2+x2y1z3-x2y3z1-x3y1z2+x3y2z1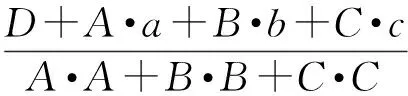
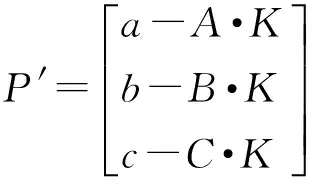
3 仿真实验

4 总结



