压缩感知在无线传感器网络数据采集中的应用
王 泉,张纳温,张金成,吕方旭,王 钰,陈可伟
(空军工程大学防空反导学院,西安 710051)
压缩感知在无线传感器网络数据采集中的应用
王 泉,张纳温*,张金成,吕方旭,王 钰,陈可伟
(空军工程大学防空反导学院,西安 710051)
提出了一种无线传感器网络中基于压缩感知的数据采集方法。通过分析信号压缩观测过程,提出了适合在硬件资源有限的传感器节点中实现的循环稀疏伯努利观测矩阵CSBM(Cyclic-Sparse-Bernoulli Measurement),该矩阵使用循环稀疏矩阵与伪随机伯努利序列,采用结构化的方法构造,具有非零元素少、良好的伪随机性、硬件易于实现等优点。仿真实验表明,与其他类型的观测矩阵相比,CSBM矩阵在一定信号重构精度前提下具有更低的压缩采样比CSR(Compress Sampling Rate)。在无线传感器网络数据采集应用中,感知节点可以通过压缩观测得到更少的观测数据,能够大大减少网络通信数据量。
压缩感知;无线传感器网络;数据采集;观测矩阵
无线传感器网络WSN(Wireless Sensor Network)是由若干低成本、低功耗的传感器节点以一定的拓扑结构组成的无线自组织网络。凭借其隐蔽、容错、部署便捷等优势,WSN在环境监测、战场侦测和监控、情报收集等领域应用广泛[1]。由于成本、体积的限制,感知节点硬件资源十分有限,其通信、计算能力受限,制约WSN发展的一项瓶颈就是功耗问题[2],如何在保证获取有用信息的前提下延长传感器节点的生存周期是目前国内外学者研究的热点。然而,传感器节点在其生存周期内数据通信消耗的能量约占总能量消耗的90%[3],可见,通过减少数据通信量,减轻通信压力,可以很大程度上延长无线传感器网络的生存周期。
压缩感知CS(Compressed Sensing)是美国学者Tao和Donoho等人最早于2004年[4]提出的一种新颖的信息采样理论,只要信号在相应变换空间具有稀疏性或近似稀疏性,就可以实现信号的低速率采集与数据压缩[5-7]。近几年来,关于压缩感知自身及其在医学检测、雷达成像、图像处理等领域的应用研究都有大量的研究成果。Baron与2005年提出的分布式压缩感知DCS(Distributed Compressive Sensing)理论[8],为压缩感知在无线传感器网络应用提供了研究思路,国内外很多学者将分布式压缩感知应用在WSN中实现了数据的压缩处理。文献[9-10]对多传感器间协作的分布式信源编码技术进行了研究,通过对信源进行基于压缩感知的编码算法,达到减少数据重复编码的目的,文献[11]通过稀疏随机投影编码方式对无线传感器网络数据进行压缩、恢复,并通过仿真分析了算法恢复效果和随机投影数目对重构归一化误差影响。
总的来看,大部分研究将压缩感知使用在了对数据的压缩上,簇成员将采集到的数据传递给簇首后,簇首根据数据的时空相关性对数据进行压缩,最后再将压缩后的数据上传至Sink节点。由此可以看出,通信数据只在簇首节点到Sink节点这一层减少了,而采集节点到簇首的通信数据并没有减少,并且,WSN中簇首节点硬件资源同簇成员节点相同,将压缩感知的压缩观测放到簇首节点效率不高,会影响信息的传递效率。本文首先研究了压缩感知理论,深入分析了信号线性观测的过程,提出了适合在硬件资源有限的传感器节点中实现的观测矩阵,在簇成员节点对信号进行压缩采样,得到较少的采样数据,能够进一步减少网络通信数据量。
1 压缩感知理论概述
1.1 压缩感知基本理论
压缩感知的核心思想是利用观测矩阵Φ把一个稀疏或可压缩的高维信号投影到一个低维空间,这个投影过程相当于通过衡量信号与一些给定波形的相关度来观测信号,从而得到一组压缩数据,然后根据信号的稀疏性先验条件,借助线性或非线性重构算法来恢复原始信号。
CS理论的实现主要包含3个关键要素:信号的稀疏性、观测矩阵的设计、重构算法的设计。
信号的稀疏性是压缩感知的前提条件,信号在特定稀疏基上稀疏性的大小决定了对其压缩感知的效率和价值。假设一个长度为N的离散实值信号X,根据调和分析理论可知,X能用一组标准正交基Ψ=[ψ1,ψ2,…,ψN]的线性组合可表示为:
(1)
式中,Ψ为N×N维标准正交基;α为信号X在该正交基上展开的系数向量,若X在该矩阵Ψ上有且仅有K个非零系数,其中K远小于N,则称X可在Ψ上稀疏表示。文献[12]指出,信号的稀疏度K越小,稀疏性越强,保证信号重构所需的测量次数越少,对其压缩感知的价值和效率越高。
对信号的感知过程就是对信号进行线性投影,即:
Y=ΦX=ΦΨα=Aα
(2)
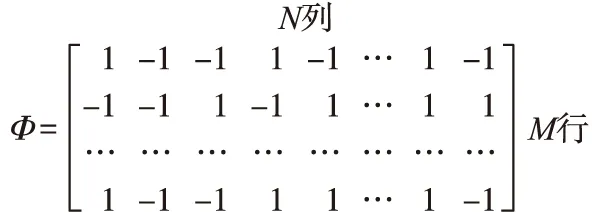
如图1所示,Φ为M×N维的观测矩阵,观测向量Y∈RM不是传统的采样点,而是信号更一般的K线性泛函。
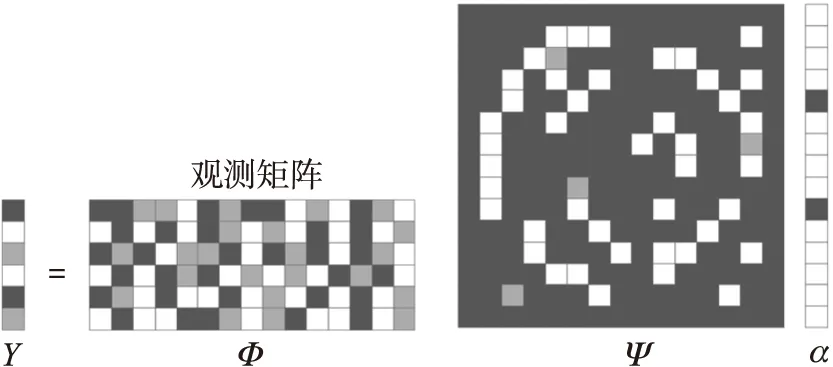
图1 压缩感知原理图
观测矩阵的设计是压缩感知的关键,Candes和Tao指出了感知矩阵A=ΦΨ(Φ为观测矩阵,Ψ为稀疏基矩阵)必须满足约束等距性条件RIP(Restricted Isometry Property),他们证明了对于任意K稀疏信号X,如果满足

(3)
式(3)中δk表示等容常数,取值范围δk∈(0,1),AT是以T为指标集抽取矩阵A的列向量形成的N×T维矩阵,通过极小范数能够唯一恢复出稀疏信号[7]。
但是,判断一个矩阵是否满足RIP,计算有限等距常数都很困难。Donoho提出了相关性判别理论,通过数学推导严谨的证明了:观测矩阵Φ与稀疏基Ψ的不相干程度越高,CS矩阵的S-受限等距常数就越大,精确重构稀疏信号所需的观测数越少[13]。两个矩阵之间的相干程度定义为:
(4)

图2 对稀疏分量的感知过程

M>C·μ2(A)·K·logN
(5)
重建信号的测量值数目必须符合式(5),其中C为常系数,K为信号在某个稀疏域的稀疏度,N为待重构信号的长度。由此可见,重构信号所需观测值的数目与观测矩阵和稀疏基的不相关程度关系密切,寻找与稀疏基不相关性好的观测矩阵,使感知矩阵A“平坦”,这样能够减少所需的测量值数目。
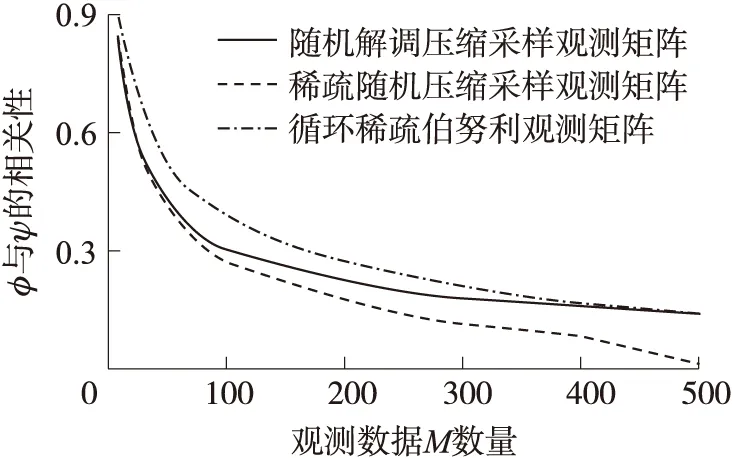
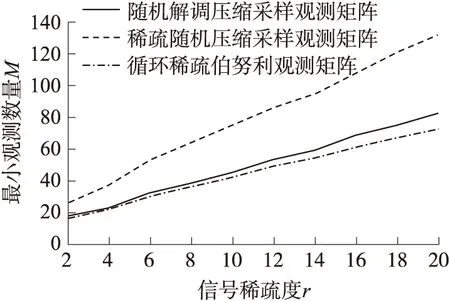
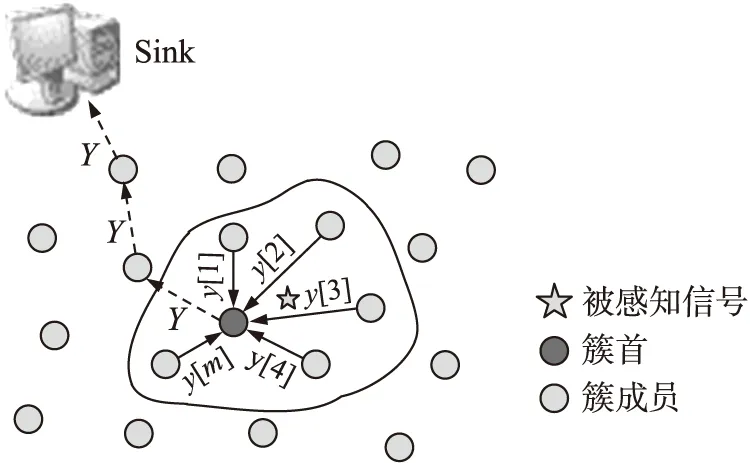
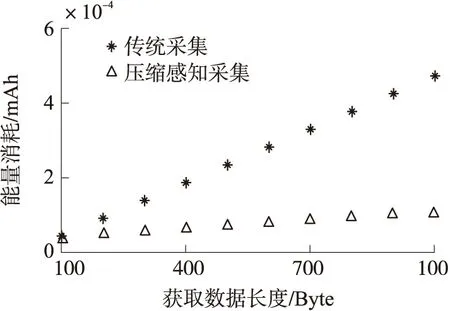
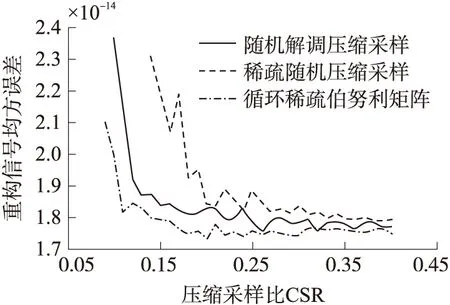
重构算法是从压缩信息中恢复原始信号的手段,也是为节约硬件资源付出的软件代价,信号的重构是指从M维的观测向量Y中重构长度为N(M< min‖X‖l0s.t.ΦΨ-1X=Y (6) 式(6)表述的问题是一个NP难的组合优化问题,实际上是无法直接求得最优解的。因此,研究人员不得不寻求次优解,现有的重构算法都是次优解算法,主要有四类:①凸优化方法;②组合算法;③统计优化方法;④贪婪算法。本文采用正交匹配算法对信号进行重构。 1.2 压缩感知数据采集 压缩感知理论起初是针对离散域的数字信号处理提出的,然而将压缩与采样合二为一才是压缩感知的创新之处,只有将它扩展到模拟时间域时在才能体现压缩感知理论实际意义。目前将压缩感知应用在模拟信号采集上的实现方法主要有:随机解调压缩采样方法[14]和稀疏随机压缩采样方法[15]。 随机解调压缩采样实现模拟信号压缩感知的过程如图3所示,首先使用随机序列以奈奎斯特频率对信号进行采样,然后通过积分器对多个奈奎斯特采样值进行累加,最后以低速ADC进行采样,从而实现对信号的压缩。可以看出该方法使用随机序列调制和积分累加的方式实现了压缩感知中的线性观测过程。 图3 随机解调压缩采样原理框图 经分析,信号经过第m个支路的乘法器与随机序列进行随机解调、积分累加后采样得到一个观测值y[m],可以表示为: (7) 其中,M为采集通道个数也为AD的个数,Te为积分时间,即整个压缩观测所用的时间,各路随机序列若均满足伯努利分布,可以提取出相应的观测矩阵如图4所示。 图4 随机解调压缩采样观测矩阵 由于该方法需要对信号进行预处理,即用伯努利随机序列进行调制,实际上并没有达到减少采样次数的目的(使用伯努利序列调制信号也是采样的过程),同时观测矩阵稠密(全为非零元素),硬件实现代价较大,不适合应用于资源受限的无线传感器网络中。 文献[15]提出的一种稀疏随机压缩采样方法,该方法的思想是从传统的采样数据中随机抽取若干采样值,然后使用普通随机观测矩阵对稀疏采样值进行压缩观测,整个压缩感知的过程如图5所示。 图5 稀疏随机压缩采样的压缩感知过程 图6 稀疏随机压缩采样观测矩阵 2.1 CSBM矩阵的构造方法 CSBM矩阵是由具有低计算复杂度和易于硬件实现的循环稀疏矩阵,以及具有良好伪随机性的伯努利序列通过结构化组合方法够造的一种新型压缩感知观测矩阵。 步骤1:首先产生循环稀疏矩阵,构造零矩阵Z=(zij)∈RM×N,其中M为压缩感知观测数量,N为原始采样数据长度,遍历零矩阵Z的列向量,根据式(8)对Z进行处理: Z(mod(j,M)+1,j)=1 (8) 此时得到循环稀疏矩阵G,其结构如图7所示。 图7 循环稀疏矩阵G结构图示 步骤2:产生伯努利序列{bj}∈{0,1},其中1≤j≤N,序列元素均独立服从伯努利分布bj~Bern(0.5),由映射f→2f-1对序列{bj}进行映射,形成双极性伪随机序列{hj}∈{1,-1},然后按照式(9)由该序列构成对角矩阵。 (9) 结构如图8所示。 图8 伪随机对角矩阵H结构图示 步骤3:将循环稀疏矩阵G与伪随机对角矩阵H根据式ΦCSBM=GH,采用结构化方法进行观测矩阵的构造,最终观测矩阵结构图如图9所示。 图9 CSBM观测矩阵结构图示 通过结构化构造得到的CSBM观测矩阵中非零元素仅有N个,各非零元素均为±1,所以CSBM观测矩阵具有快速计算的性能,而且易于硬件实现。 下面考察循环稀疏伯努利观测矩阵与傅里叶稀疏基的不相干性与信号重构性能,与前文提到的两种观测矩阵进行对照,本文选取信号长度N=500,通过改变观测数量M从而改变压缩比,不同压缩比下三个观测矩阵与傅里叶基的相关性对比如图10所示。 图10 观测矩阵相关性对比分析 同时,对三个观测矩阵进行信号重构能力对比测试:在不同稀疏度下高概率精确重构信号(本文规定精确重构信号成功率达到80%即为高概率精确重构信号)所需最小观测数量M如图11所示。 图11 观测矩阵信号重构性能对比分析 通过对比可以看出,在相同的压缩比下,稀疏随机压缩采样的感知矩阵的不相干性最差,这是由于稀疏随机压缩采样丢掉了传统采样数据中一些有用的信息,由式(5)可知,在相同的信号稀疏度下,稀疏随机压缩采样需要更多的观测值。此外,由于稀疏随机压缩采样要求采样间隔要满足特定的高斯分布,实现这种采样序列对于一般的AD转换器是困难的[3]。在同等压缩比下,循环稀疏伯努利矩阵与稀疏基有更好的不相关性,这说明在同等信号稀疏度下,使用循环稀疏伯努利矩阵作为观测矩阵所需的观测量更少。同时,从循环稀疏伯努利矩阵的结构可以看出,观测矩阵的每一行两个相邻非零元素的间隔相同,这样,采集节点就可以以较低的采样速率匀速采样,这种采样方式普通模数转换器容易实现。 2.2 压缩感知在WSN中的实现方法 在实际应用中,考虑到WSN是由大量传感器节点构成的,可以通过网络协议形成“信息感知簇”,由簇首将观测矩阵中M个行向量包含的伯努利序列分发给每个簇成员即采集节点,每个采集节点按照低速率采样得到采样数据,然后与接收到的伯努利序列进行简单运算得到一个压缩观测值,每个采集节点只需向簇首发送一个压缩观测数据即可,簇首将接收到的压缩观测数据向Sink节点传递,由Sink节点完成信息的解压缩和信息的提取,整个数据采集过程如图12所示。 图12 WSN中压缩数据采集图示 2.3 WSN中压缩感知能耗分析 无线传感器网络中完成一次数据采集任务的能耗计算公式为:无线通信能耗=发送能耗+接收能耗,其中,发送能耗=发送瞬时电流×发送一字节的时间×发送总字节数;接收能耗=接收瞬时电流×接收一字节的时间×接收总字节数。在普通5 V电池供电下,节点在发射和接收时所需要的瞬时电流分别为29 mA和24 mA,每发送一个字节需要耗时32 μs[3]。 假设获取数据为长度N的单字节数据,传统WSN数据采集的方式在网络中需要发送和接收N个字节的数据;而基于压缩感知的数据采集方法网络中需要发送和接收的数据有M字节压缩观测值、M字节采样启动时延以及采样加权向量,采样加权向量通过二进制编码能够转换为N/8字节的数据,由式(5)可知,在确定的观测矩阵下,压缩观测数据长度M∝log(N)。 依上所述,传统数据采集方法网络通信数据总量为:BT=N字节;基于压缩感知的数据采集方法网络通信数据总量为:BD=clog(N)+N/8字节,c为正常数。 根据数据采集通信能耗的计算公式,分别对两种数据获取方式的能量消耗进行了仿真分析。图13为通信能耗与采集数据长度的关系。 图13 能量消耗对比图示 可以看出随着采集数据长度的增加,两种数据收集方法的网络通信能耗均增加,但基于压缩感知的数据收集方法网络能耗增加速度远远小于传统采样的网络能耗,并且随着采集信号长度的增加,能量节省效果越明显。 根据第3节中构造出的循环稀疏伯努利矩阵,本文选取长度N为500的稀疏度为K=20的谐波信号作为测试对象,验证采用循环稀疏伯努利观测矩阵对信号压缩感知的性能,并给出随机解调压缩采样观测矩阵、稀疏随机压缩采样观测矩阵的精确重构信号成功率对比结果。 实验中,信号重建性能采用均方误差(MSE)作为性能评价指标如式(10)所示: (10) 实验规定,重构信号与原始信号均方误差MSE小于10-5为精确重构,为简化问题,本文不考虑信号采样过程中引入的噪声问题,在理想条件下对不同观测矩阵的信号重构性能做出对比分析,分别在不同压缩采样比CSR=N/M下给出三个观测矩阵的信号重构成功率,如图14所示。 图14 精确重构信号成功率对比 可以看出,在同等压缩采样比CSR下,循环稀疏伯努利观测矩阵精确重构信号成功率优于随机解调压缩采样观测矩阵和稀疏随机压缩采样观测矩阵。 图15 重构信号均方误差对比分析 在三种观测矩阵下,图15给出了重建性能指标的对比分析,从重构信号均方误差角度看,相比于其他两个观测矩阵,循环稀疏伯努利矩阵有更好的重构性能,而且在压缩比较小时性能优势更为明显。 结合压缩感知理论对常见的两种压缩感知硬件实现方式进行分析,提出一种循环稀疏伯努利观测矩阵,该矩阵在相关性和信号重构性能上均优于已知的两种观测矩阵:随机解调压缩采样观测矩阵和稀疏随机压缩采样观测矩阵。该矩阵稀疏的结构特点适合WSN传感节点进行均匀低速采样,采取发送压缩观测值的策略大大减少了网络通信数据量,具有较高的应用意义。 [1] 吕方旭,张金成,刘立阳,等. 基于WSN的多声源目标定位算法[J]. 传感技术学报,2012,25(8):1121-125. [2]张金成,吕方旭,王钰,等. WSNs中的分簇式压缩感知[J]. 仪器仪表学报,2014,35(1):169-177. [3]Lan F,Akyildiz,Mehmet Can Vuran. Wireless Sensor Networks[M]. America:John Wiley and Sons,2010,46-49. [4]石光明,刘丹华,高大化,等. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5):1070-1081. [5]Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306. [6]Candes E,Romberg J,Tao T. Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory,2006,52(2):489-509. [7]Candes E. The Restricted Isometry Property and Its Implications for Compressed Sensing[J]. C R Math Acad Sci Paris,2008,346(9-10):589-592. [8]Dror Baron,Marco F,Duarte. Distributed Compressive Sensing of Jointly Spares Signals[C]//Asilomar Conference on Signals,Systems and Computers,IEEE Press,2005:1537-1541. [9]Luo Chong,Sun Jun,Wu Feng. Compressive Network Coding for Approximate Sensor Data Gathering[C]//Global Telecommunications Conference,IEEE Press,2011:1-6. [10]吕方旭,张金成,石洪君,等. WSN中的分布式压缩感知[J]. 传感技术学报,2013,26(10):1446-1452. [11]Gastpar M,Dragotti P L,Vetterli M. The Distributed Karhunen-Loeve Transform[J]. IEEE Transactions on Information Theory,2006,52(12):5177-5196. [12]Candes E,Tao T. Near-Optimal Signal Recovery from Random Projections and Universal Encoding Strategies[J]. IEEE Transactions on Information Theory,2006,52(12):5406-5425. [13]Donoho D L,Huo X. Uncertainty Principles and Ideal Atomic Decomposition[J]. IEEE Transactions on Information Theory,1999,47(7):2845-2862. [14]Candes E J,Wakin M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine,2008,25(2):21-30. [15]余恺,李元实,王智,等. 基于压缩感知的新型声音信号采集方法[J]. 仪器仪表学报,2012,33(1):105-112. 王泉(1990-),男,硕士研究生,研究方向为信号与信息处理,无线传感器网络,wangquan628@126.com; 张纳温(1975-),女,硕士,副教授,硕士生导师,研究方向为信号与信息处理,微处理器技术,673632209@qq.com。 CompressedSensingforDataCollectioninWirelessSensorNetwork WANGQuan,ZHANGNawen*,ZHANGJincheng,LÜFangxu,WANGYu,CHENKewei (Air Force Engineering University,Air and Missile Defense College,Xi’an 710051,China) An efficient data collection method in wireless sensor network(WSN)was proposed based on Compressed Sensing(CS). Firstly,the Cyclic-Sparse-Bernoulli Measurement(CSBM)matrix was presented which is suitable for application in resource-constrained sensor node. The CSBM matrix is constructed using the structured approach with cyclic-sparse matrix and Bernoulli pseudo-randomness sequence,which have a series advantages,such as less nonzero elements,good property of pseudo-randomness and easy implementation in hardware. The Simulation and experiment show that considering the precision of signal reconstruction,the CSBM matrix can reach the less compress sampling rate(CSR)compared to other types of measurement matrix. In the application of data collection in WSN,the sensor node can acquire less data through CS measurement,which reduce data traffic in WSN. compressed sensing;wireless sensor network;data collection;measurement matrix 2014-07-13修改日期:2014-09-21 10.3969/j.issn.1004-1699.2014.11.022 TP393 :A :1004-1699(2014)11-1562-06

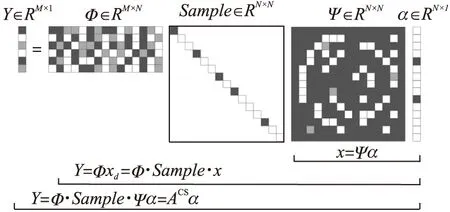


2 WSN中的压缩感知

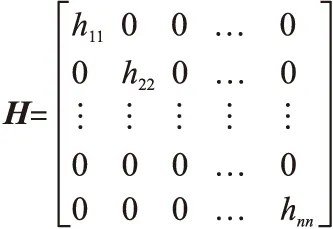
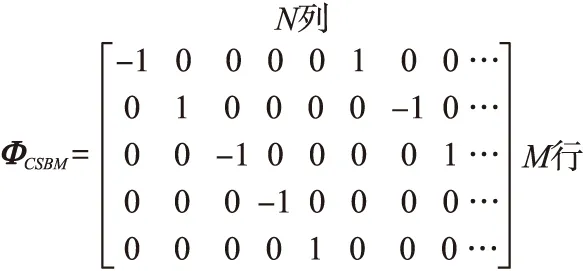
3 仿真实验及分析

4 结论



