一种基于Taylor和Kalman的室内协同定位方法*

王瑞荣,郑书万,陈浩龙,薛 楚

(1.杭州电子科技大学生命信息与仪器工程学院,杭州 310018;2.杭州电子科技大学信息与控制研究所,杭州 310018)



一种基于Taylor和Kalman的室内协同定位方法*

王瑞荣1*,郑书万2,陈浩龙1,薛 楚1

(1.杭州电子科技大学生命信息与仪器工程学院,杭州 310018;2.杭州电子科技大学信息与控制研究所,杭州 310018)

结合Chan算法、Taylor算法及Kalman算法三种TDOA算法的优点,提出一种能应用于室内实时定位的协同方法。首先基于Chan与Taylor的协同定位方法估算位置信息,并通过对估计结果的残差设置阈值来鉴别NLOS,从而抛弃受到NLOS污染严重的测量数据。其次,再对符合条件的测量数据,利用Kalman方法计算定位结果,与Taylor方法的定位结果通过设置判别条件进行比较,以此进一步抑制NLOS干扰。对符合判别条件的定位结果,进行残差加权及移动平均加权处理,从而完成最终定位结果的更新。最后,利用室内实时定位实验,证明该方法能有效过滤受到NLOS污染严重的测距数据,提高定位精度,并且具有良好的稳定性。

室内定位;协同方法;Taylor算法;Kalman算法;残差加权

随着物联网和智慧城市建设的兴起和发展,数据和多媒体业务快速增加,带动了室内定位应用服务需求日益增加。但是,相比室外定位环境,室内环境空间封闭狭小,障碍物多,无线信号不仅存在多径传播效应,且易受到空间随机无线电波信号干扰。室内环境的复杂多变,要求定位系统具有良好的抗干扰性、适应性。目前,常见的室内定位方法有基于测距和非测距两种方法。相对而言,基于测距的方法具有更高的定位精度,且更具有应用价值。常见基于测距的定位算法有时间到达法TOA(Time of Arrive)、时间到达差法TDOA(Time Difference of Arrival)、信号强度法RSSI(Received Signal Strength Indication)、到达角度法AOA(Angle of Arrival)等[1]。这些方法又有各自的特性,RSSI测量值在实际应用中规律性较差,利用RSSI信息难以得到较高的定位精度;AOA测量虽然精度较高,但传感节点成本高,能耗大;TOA和TDOA测量方法简单,传感器节点成本适宜,且能得到较高定位精度,使得这两种方法广泛应用。TDOA算法是对TOA算法的改进,其计算过程更加简单,精度也有所提高,只需基站之间同步[1-2]。因此,文中研究一种抑制NLOS(Non Line of Sight)的室内TDOA定位方法。

典型的TDOA定位算法有Fang算法[3]、Chan算法[4]、Taylor展开算法[5]、Kalman算法[6]等。Chan算法计算过程中,采用两步加权最小二乘估计定位结果,具有运算快特点。在信道环境较差情况下,虽然其定位精度可能迅速下降,但估计结果仍能反映与TDOA测量值之间的大致特征[7-8]。Taylor和Kalman算法都能获得较为准确的定位估计值[9-11]。但是,Taylor算法需要设置合适的初始值,否则可能导致定位算法不收敛。Chan和Taylor的协同方法[12],将Chan方法的定位结果作为Taylor方法的初始位置结果,可保证其收敛性。Kalman算法对历史定位数据具有记忆性,若历史数据出现较大偏差,将对系统定位结果持续产生负面影响。因此需要对受到NLOS干扰严重的测量数据进行识别处理,从而提高Kalman算法的定位精度。文中利用定位结果残差鉴别受到NLOS污染严重的测距数据,并对其进行抛弃处理。

同时,适用于室内环境定位的无线技术有超宽带技术(UWB)、线性调频扩频技术(CSS)、Zigbee技术、Wifi技术等。其中,基于CSS技术的定位设备,利用对称双路双边测距方式(SDS-TWR)测量节点间距离,具有发射功率低、测距精度高、通信稳定性好、抗干扰能力强等特点,适用于室内定位[13-15]。文中采用基于CSS技术的定位设备对定位算法进行实验分析。

1 TDOA定位算法描述

在二维空间内,TDOA双曲线数学模型如下:

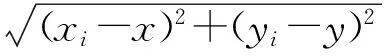
(1)

其中,(xi,yi),i=1,2,3….,n为基站节点坐标,(x,y)为目标节点坐标,ri1是第i(i≤2)个基站与第1个基站到目标节点的距离差,ni1是相对应的TDOA测距误差。

1.1 Chan算法

Chan算法[4]是一种利用求解双曲线方法的非递归算法。求解过程中,对式(1)进行线性化处理,两次利用最小二乘法(WLS)加权估计结果。第一次估计忽略目标节点的坐标(x,y)与基准基站间的距离者之间的相关性,作为独立变量求解;第二次估算则利用三者之间的约束关系,得到更加准确的目标节点标值。对于Chan算法的估计结果,当系统噪声服从高斯分布时,误差较小;否则,精度将迅速下降。

1.2 Taylor算法

Taylor算法[5]是一种需要目标节点初始估计位置的递归算法。求解过程中,估计坐标(x,y)表示为:

式中,(x0,y0)初始估计位置,Δx和Δy是估计误差。

对式(1)在初始点(x0,y0)进行Taylor级数展开,忽略二阶以上分量,建立求解TDOA测量误差矢量的线性方程。然后,根据局部线性最小二乘解法估计坐标误差。以此,迭代更新目标节点的估计位置直到坐标误差满足预先设置的门限。但是,如果初始位置的设置不恰当,可能导致算法运算结果发散,且对不收敛的情况无法进行事先判断。

1.3 Kalman算法

Kalman算法[6]是利用扩展Kalman滤波(EKF)两次递归估算求解的算法。基于式(1),建立线性的状态方程和非线性的观测方程分别为:

式中,Xk=[xk,yk,vxk,vyk]T是tk时刻状态向量,(xk,yk)是目标节点坐标信息,(vxk,vyk)是目标节点x方向和y方向的分速度,Φ是状态转移矩阵,h(Xk)是非线性量测函数,Yk=[r21,r31,…,rn1]T是量测数据向量,Wk-1、Vk是输入噪声和观测噪声。

非线性的观测方程,需利用Taylor级数展开得到雅可比矩阵,用非线性函数的局部线性化特性来近似描述其非线性。然后利用EKF算法方程估计定位结果。Kalman算法利用历史定位数据进行估算,具有较好的动态定位性能。但若历史定位数据出现较大偏差,将持续影响定位结果的估算。

2 基于Taylor和Kalman的协同定位方法

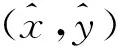
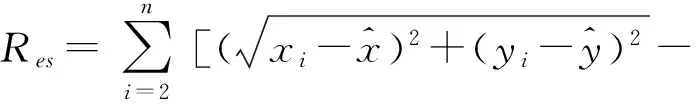
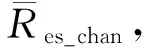
然后,对仍然符合条件的测距数据,用Kalman方法计算得到位置结果(x3,y3),并与(x2,y2)进行比较,进一步过滤测量数据。对于Taylor方法和Kalman方法,在测量值误差不大情况下,定位结果应相近。以此,设置阈值δ3、δ4,建立如下两种不同判断不等式:

|x3-x2|+|y3-y2|<δ3

(2)

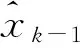
(3)

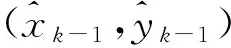
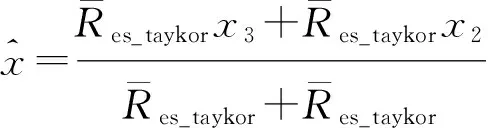
(4)

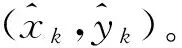
阈值δ1、δ2、δ3和δ4的选取主要根据定位设备的测距精度,及在室内环境下的历史定位信息。根据定位设备定位精度,选取δ1、δ2(δ1>δ2),确保误差非常大的测距数据能有效过滤,减少计算量。然后利用历史测量数据,用Chan和Taylor的协同方法计算定位结果,舍去定位误差大的定位结果及相对应的测量数据,再用Kalman方法计算位置结果。统计Taylor方法定位结果的残差平方和均值和与Kalman方法定位结果的差值,确定合适的δ3和δ4,确保能使历史数据基本满足式(2)和式(3)的判断不等式。δ3和δ4选取应适宜,过大则降低对NLOS抑制的能力,过小则会对测量数据误判,去除有效的测距数据。同时,根据实时定位信息,微调阈值。

3 实验设计和数据分析

3.1 实验设计

定位测试实验使用Nanotron公司生产的nanoLOC Development Kit 3.0设备,在杭州电子科技大学第二教学楼南504实验室进行。该实验室长8.3 m,宽8.5 m。同时,室内环境较为复杂,摆放有多台办公桌、计算机及其它仪表仪器,人员走动频繁。在实验室中取5.65 m×5.4 m的区域并布置四个基站节点:Anchor1(0.00,0.00),Anchor2(5.65,00.00),Anchor3(5.65,5.40),Anchor4(0.00,5.40),然后在该区域中放置一个目标节点。

设备使用手册介绍,在LOS情况下,定位设备理论上的测距精度能达到2 m。但经过室内测距实验,表明测距误差大于2 m,在3～4 m左右,但是都是误差都是正值且都大于2 m。所以,估计Chan方法定位残差误差在4 m左右,Chan和Taylor的协同方法定位残差在0.64 m左右。最终根据历史定位信息,选取δ1=4.0 m、δ2=0.64 m、δ3=0.14 m、δ4=0.5 m。

实验过程中,先将目标节点放置固定位置,然后对定位设备的TOA测量结果实时采集并保存。同时,对TOA值进行重构得到TDOA值,利用文中提出的定位算法实时估算目标节点位置并保存,同时图形化显示,如图1所示。

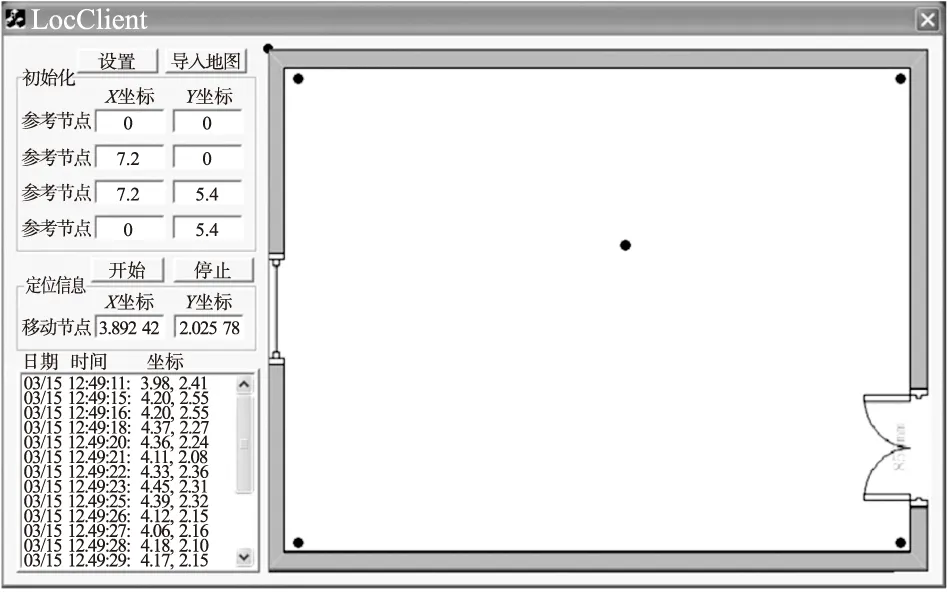
图1 目标节点位置信息实时显示

为了检验文中提出的算法是否能有效抑制NLOS干扰,将重新采用最小二乘(LS)TOA方法,Chan方法、Taylor方法及Kalman方法估算定位结果,并与其进行比较分析。同时,挑选两组原始定位数据,通过Chan_Taylor协同方法、Kalman方法、定位结果残差设置阈值的Chan_Taylor协同方法(设置的阈值分别为δ1和δ2)以及文中方法分别进行计算定位结果误差,并进行比较分析。

3.2 数据分析

对目标节点进行多次定位实验后,比较采用LS TOA方法、Chan方法、Taylor方法、Kalman方法及文中方法计算得到的定位结果均值,如表1所示。比较Taylor方法、Kalman方法及文中方法定位结果的均方根误差(RESE),如表2所示。

表1 不同算法目标节点估计坐标值比较

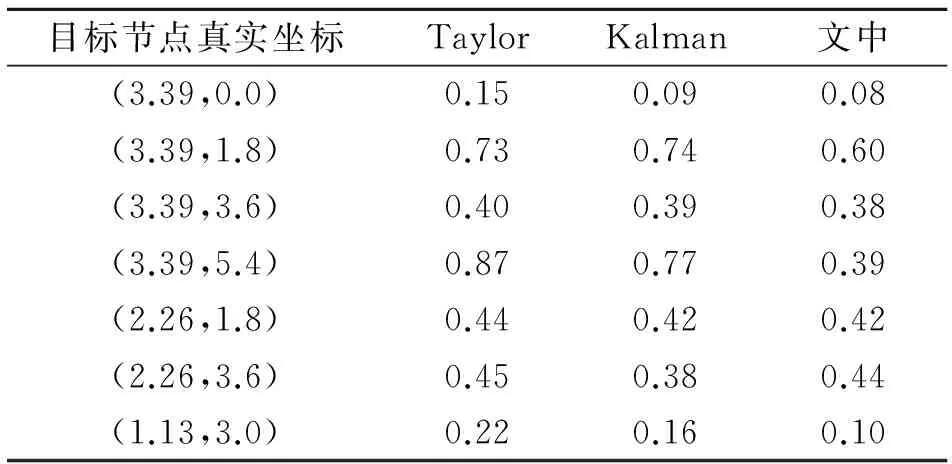
表2 不同算法估计结果的RMSE比较

从表中数据看出,在室内环境下,采用LS TOA方法和Chan方法得到的定位结果较差,具有较大定位误差,所以这两种方法不适合室内定位;Taylor方法和Kalman方法的定位精度较高,结果接近真实值,并且两者定位结果相接近;文中结合基于Chan算法、Taylor方法和Kalman方法的协同定位方法,结合两者算法优点,具有更高的定位精度。进一步比较三者算法的RMSE表明,文中定位方法稳定性也更好。

取目标节点放置在(3.39,5.40)和(2.26,1.80)位置的原始测量数据,然后分别利用Chan_Taylor协同方法、Kalman方法、定位结果残差设置门限的Chan_Taylor协同方法及文中方法估算定位结果并计算定位误差。图2和图3是目标节点在(2.26,1.80)位置的定位误差比较,图4和图5是目标节点在(2.39,5.40)位置的定位误差比较。

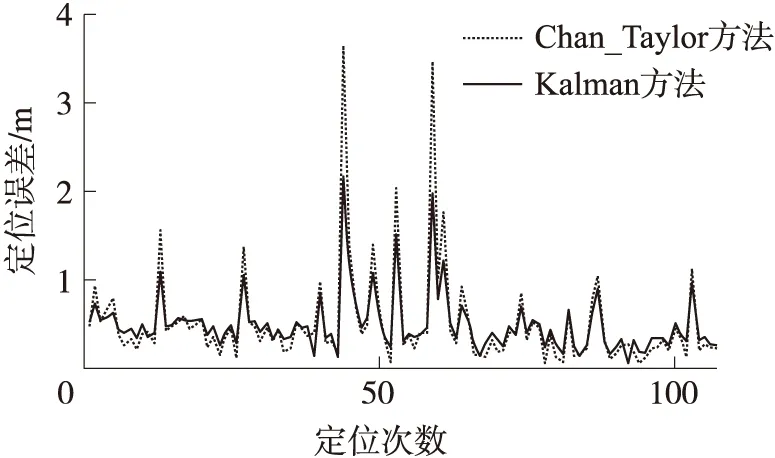
图2 比较Chan_Taylor和Klaman在坐标(2.26,1.8)定位误差

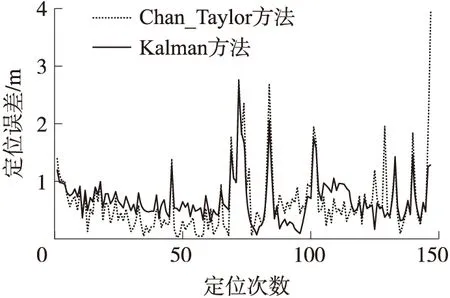
图3 比较Chan_Taylor和Kalman在坐标(3.39,5.40)定位误差

图4 比较文中方法和残差设置阈值的Taylor方法在坐标(2.26,1.80)定位误差

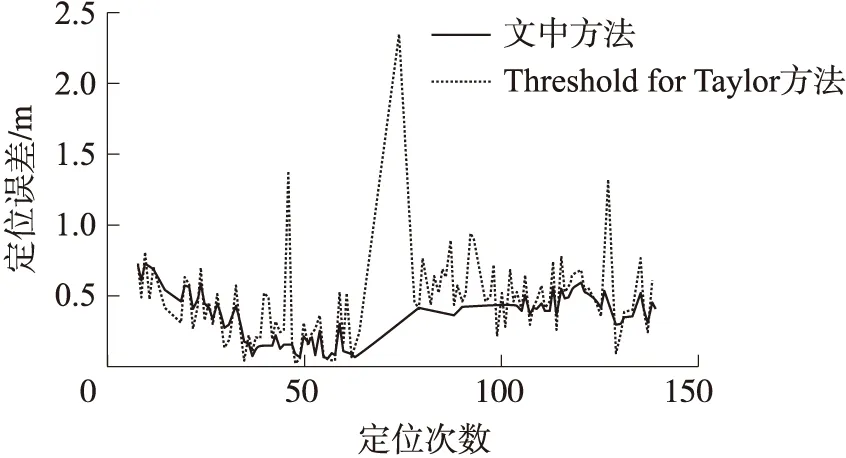
图5 比较文中方法和残差设置阈值的Taylor方法在坐标(3.39,5.40)定位误差

利用Chan_Taylor协同方法和Kalman方法估算定位结果,计算定位误差,如图2与图4所示。图中表明,定位结果受到NLOS的影响明显,误差波动幅度较大。

而图3和图5表明,对Chan与Taylor协同方法的定位结果残差设置阈值,虽具有过滤受到NLOS污染的测量数据,来改善定位结果误差的能力,但仍有误差较大的定位结果,需进一步过滤原始测距数据,来抑制NLOS干扰;同时,文中提出的方法更加有效的过滤受到NLOS污染的测量数据,使定位结果未出现较大误差,基本保持在一定范围内,波动幅度小,NLOS得到抑制。

从实验结果看出,文中提出的定位方法能有效抑制NLOS干扰,使定位误差减小,对于室内定位具有一定的实用性。

4 结束语

文中结合Chan算法、Taylor算法及Kalman算法三者算法特点,提出一种室内定位协同方法。实验结果表明,文中提出的室内定位方法能有效抑制室内环境下的NLOS干扰,具有较高的定位精度,具有良好的稳定性,在室内定位具有一定的实用价值。改进现有的算法,对受NLOS污染严重的测量数据,也可以进行消极加权和统计校正处理,从而抑制NLOS;对测量数据进行预处理,减少NLOS影响,及对定位结果进行数据滤波处理,提高定位精度等,都是文中接下来的研究工作。

[1] 彭宇,王丹. 无线传感器网络定位技术综述[J]. 电子测量与仪器学报,2011,25(5):389-399.

[2]张丽. 超宽带室内精确定位技术研究[D]. 青岛:中国海洋大学,2012:21-40.

[3]Fang B T. Simple Solutions for Hyperbolic and Related Position Fixes[J]. IEEE Trans on Aerospace and Electronic Systems,1990,26(5):748-753.

[4]Chan Y T,Ho K C. A Simple and Efficient Estimator for Hyperbolic Location[J]. Signal Processing,IEEE Transactions,1994,42(8):1905-1915.

[5]Foy W H. Position-Location Solutions by Taylor Series Estimation[J]. IEEE Trans Aerosp Electron Syst,1976,12(2):187-194.

[6]Najar M,Vidal J. Kalman Tracking Based on TDOA for UMTS Mobile Location[C]//Proc IEEE Int Symp Personal,Indoor and Mobile Radio Communication(PIMRC). San Diego,CA,2001:B45-B49.

[7]桂忠,董利达,兰守珍. 一种在非视距环境中的移动节点定位方法[J]. 浙江大学学报(理学版),2009,36(1):52-56.

[8]Ho K C. Bias Reduction for an Explicit Solution of Source Localization Using TDOA[J]. IEEE Transactions on Signal Processing,2012,60(5):2101-2114.

[9]Kovavisaruch L,Ho K C. Modified Taylor-Series Method for Source and Receiver Localization Using TDOA Measurements with Erroneous Receiver Positions[C]//Proc of IEEE International Symposium on Circuits and Systems(ISCAS). IEEE Press,2005:2295-2298.

[10]Rullan-Lara J,Salazar S,Lozano R. UAV Real-Time Location Using a Wireless Sensor Network[C]//Proc of IEEE Positioning Navigation and Communication(WPNC). Dresden,German:IEEE Press,2011:18-23.

[11]Chiang ChengTse,Tseng PoHsuan,Feng KaiTen. Hybrid Unified Kalman Tracking Algorithms for Heterogeneous Wireless Location Systems[J]. IEEE Transactions on Vehicular Technology,2012,61(2):702-715.

[12]刘林,邓平,范平志. 基于Chan氏算法和Taylor级数展开法的协同定位方法[J]. 电子与信息学报,2004,26(1):41-46.

[13]杨清玉,于宁,王霄,等. 无线传感器网络线性调频扩频测距方法研究[J]. 传感技术学报,2010,23(12):1761-1765.

[14]Nanaotron Technologies GmbH. Nanotron Chirp Based Wireless Networks,White Paper,V1.04[EB/OL]. http://nanotron.com/EN/pdf/WP_CSS.pdf.

[15]段翠翠,王瑞荣,王建中,等. 无线传感器网络的高危生产区人员定位系统[J]. 传感技术学报,2011,25(11):1599-1602.

王瑞荣(1973-),男,浙江义乌人,博士,副教授,主要研究方向为智能仪器;

郑书万(1991-),男,浙江平阳人,硕士在读,主要研究方向为无线传感器网络。

AnCooperativeLocalizationMethodBasedonTaylorandKalmanAlgorithms*

WANGRuirong1*,ZHENGShuwan2,CHENHaolong1,XUEChu1

(1.College of Life Information Science & Instrument Engineering,Hangzhou Dianzi University,Hangzhou 310018,China;2.Institute of Information and Control,Hangzhou Dianzi University,Hangzhou 310018,China)

A cooperative method for indoor real-time localization based on three TDOA algorithms is presented. These algorithms are Chan algorithm,Taylor serials expansion algorithm,and Extended Kalman filter algorithm. Firstly,estimation result is calculated by a cooperative method based on Chan and Taylor and threshold value of its residuals is set to identity NLOS and discard the ranging data that is disturbed severely by NLOS. Then,Kalman method is used for the matching data to get estimation position. The location result of Kalman is compared with the result of Taylor through setting some condition to further restrain NLOS error. Next,the final estimation result is obtained,by using residual weighting algorithm and moving weighted average method to the meet results. Finally,the experimental results show that this method can restrain NLOS error efficiently and improve the precision of location.

indoor localization;cooperative method;Taylor algorithm;Kalman algorithm;residual weighting

项目来源:国家自然科学基金项目(61374005);浙江省重大科技专项项目(2011R09019-01)

2014-06-23修改日期:2014-09-15

10.3969/j.issn.1004-1699.2014.11.021

TP393

:A

:1004-1699(2014)11-1557-05