模糊算法在混合储能系统中的应用及仿真
宋宏伟,吕玉祥*,王启银,赵 锐
(1.太原理工大学物理与光电工程学院,太原 030024;2.大同电力分公司,山西 大同 037008)
模糊算法在混合储能系统中的应用及仿真
宋宏伟1,吕玉祥1*,王启银2,赵锐2
(1.太原理工大学物理与光电工程学院,太原 030024;2.大同电力分公司,山西 大同 037008)
摘要:设计了基于2种直流功率变换器的蓄电池—超级电容器并联控制系统,针对混合储能系统充放电过程具有非线性、时变性、滞后性的特点,提出了一种基于模糊算法的储能系统优化控制策略,并在MATLAB/Simulink进行了建模和仿真。仿真和实验结果表明采用新型的控制策略,不仅能够在保持直流母线电压稳定的同时提高储能系统的功率输出能力,而且有效改善传统算法控制中极易产生系统振荡的弊端,优化蓄电池的工作过程从而延长其寿命。
关键词:混合储能;模糊算法;建模与仿真;超级电容器;蓄电池
随着社会的发展与科技的进步,越来越多的设备要求电源具有较高的瞬时功率输出能力,如移动数字设备、电动汽车、军事武器等,其特点是峰值功率很高,但平均功率较低,而且输出频率具有随机性。蓄电池具有功率密度小和循环寿命短等缺点,如果采用蓄电池作为这种用电设备的电源,一方面需要配置很大的容量才能满足负载的峰值功率需求,另一方面在输出频率较高的大功率时会造成蓄电池循环寿命大幅缩减。超级电容器的优点是功率密度大,储能效率高,充放电速度快,循环寿命长,缺点是能量密度和单体电压较低,还不能广泛应用于大容量、高电压的电力储能场合。如果将二者混合使用,可以优势互补,不仅能够增加混合储能系统功率输出能力,提高其耐压等级,延长蓄电池使用寿命,而且也可为高电压的电网储能研究提供一定参考价值[1-2]。
蓄电池和超级电容器的混合方式通常为通过功率变换器并联,以便在电压匹配以及容量匹配有着更大的灵活性。文献[3]对超级电容器——蓄电池组成的复合电源进行了相关试验研究,通过使复合电源输出周期性的规则和不规则方波来测量其各种性能,验证了超级电容器在改善脉冲功率输出能力和提高整个系统寿命有着极其重要的作用。文献[4]提出了一种变增益的单极点—单零点补偿网络作为电流控制器来控制基于Boost功率变换器的超级电容器——蓄电池并联储能系统,基本实现蓄电池放电电流恒流控制。文献[5]采用传统的PID控制器实现对并联储能系统的控制,一定程度减小蓄电池的放电电流。实际上,超级电容器和蓄电池本身在充放电过程中就具有非线性,两者若组成混合系统,非线性将会增加,因此采用传统的线性控制算法很难保证系统的可控性及稳定性,甚至会造成系统剧烈振荡。本文采用双向功率变换器和Boost功率变换器作为并联控制器,采用模糊控制器代替以往的PID控制器,并在MATLAB/Simulink进行了建模和仿真,实验结果验证了混合储能系统结构和控制策略的有效性。
1 混合储能系统结构及基本原理
1.1混合储能系统整体结构
图1为混合储能系统整体结构框架图。混合系统中蓄电池作为主要供电单元,超级电容器组作为辅助供电单元。蓄电池通过Boost功率变换器给负载供电,超级电容器组通过双向DC-DC功率变换器给负载供电,负载要求电压稳定在DC48V。当负载以低功率正常运行时,蓄电池几乎提供全部能量;当负载发生变化,功率大幅升高时,直流母线电容会迅速弥补负载所需的大功率,储能减小,电压下降。电压采集单元会把直流母线电压的变化快速反映到模糊控制器中,模糊控制器根据模糊规则实时平稳地调整功率变换器的开关管占空比,从而实现平抑脉冲功率波动和保持直流母线电压稳定。超级电容器功率密度大,对功率突变有较高的响应能力,因此在负载功率突增过程中主要由超级电容器负责供电,避免了蓄电池大电流放电。为了避免超级电容器组可能过度放电,因此系统附加了阈值判断。
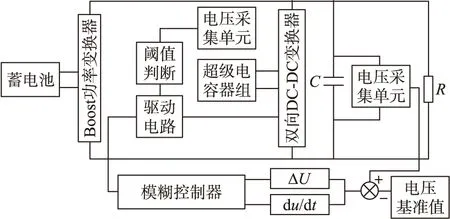
图1 混合储能系统整体结构框架图
1.2混合系统的简易数学模型
超级电容器电感很小,通常的数学模型为一个理想电容器与一个阻值很小的电阻相串联。蓄电池容量较大,短时间内小电流放电不会对蓄电池电压产生大的影响,故一般将蓄电池等效成一个恒压源和一个电阻串联的简易模型。
图2为忽略开关管影响的混合储能系统等效电路及其戴维南等效电路。C为超级电容器等效电容,Res为其等效串联电阻,ic为流过超级电容器的电流,Ub为蓄电池电压,Rb为蓄电池内阻,ib为流过蓄电池的电流,i0为系统的总输出电流。
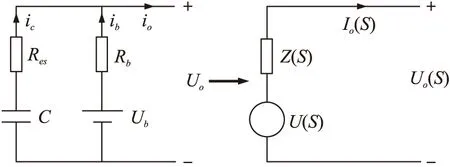
图2 蓄电池-超级电容器混合储能系统等效电路图
根据戴维南定理可得:
(1)
(2)
若负载电流为周期为T,占空比为d,幅值为I0的脉冲波,则负载电流前N个脉冲可表示为:
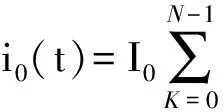
(3)
式中φt为t=0时的单位阶跃函数。
可求得内部电压降落为:
ΔU=Z(S)I0(S)
(4)
即
(5)
1.3DC-DC功率变换器
DC-DC变换器是连接于负载和电源之间的具有固定频率的开关控制装置,它的作用是在电源电压一定的变化范围内保持输出电压的恒定。本文中使用Buck-Boost变换器和Boost型变换器构成储能系统并进行了仿真,且它们均工作于电感连续导电模式状态[6]。
Buck-Boost功率变换器的电压增益M为:
(6)
Boost功率变换器的电压增益M为:
(7)
式(6)、式(7)中,DC为开关管占空比,US为输入电压,U0为输出电压。
1.4超级电容器串并联方案
目前,超级电容器单体电容能量密度和单体电容电压都比较低,所以必须将多只电容器串并联,构成超级电容器储能组以满足电压和能量的等级要求。设超级电容器组由m×n个其单体构成,内阻和电容量分别为RES和C,m为串联只数,n为并联支数。则该超级电容器组总的等效内阻为:
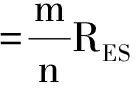
(8)
总的等效电容为:
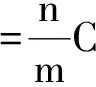
(9)
设整个放电过程超级电容器单体的电压变化范围U1~U2,超级电容器组释放的总能量为:
(10)
由式(10)可知,超级电容器释放的能量只与电压变化的范围有关,与其连接方式无关。但超级电容储能单元能量密度较低,端电压在放电过程中下降比较迅速,必须附加DC-DC功率变换器才能作为恒压源使用。上式计算出来的m×n未能考虑在功率变换器的影响与超级电容器组的储能效率,因此与实际的匹配方案有一定偏差。本文主要引入功率法来计算匹配方案[7]。
假设超级电容器组恒功率放电,系统要求输出功率为P0,运行时间为t(s)。U额为单体超级电容器的额定电压。t时刻时,其电压下降到UC(t),输出端电压到达变换器的最低工作电压Umin,储能组停止工作。
根据功率平衡和电压关系有下式成立:
(11)
(12)
式中:IC(t)为t 时刻流过超级电容器的电流。
UC(t)越小,超级电容器组释放的能量越多,储能利用率也就越高。对式(12)计算不等式极值,此时有
UC(t)=2Umin
(13)
定义超级电容器储能组的实际输出效率为η=η1×η2。其中η1为功率变换器的效率,一般在90% 以上;η2为超级电容器的储能效率,通常取80%。
(14)
增加一系数K,以减小其性能参数的不均一性带来的误差。结合式(10)、式(13)、式(14)得:
(15)
2 模糊控制器的设计
传统控制理论要求被控对象有清晰的数学模型,一般用来解决线性、时不变性等相对简单的被控系统的控制问题。模糊控制不依赖于控制系统的数学模型,而是依赖于由操作经验转换城的模糊规则,所以实现了人的某些智能,属于一种智能控制[8-9]。模糊控制一般主要由模糊化、模糊推理以及去模糊化3大部分组成。
负载电压以及功率的波动基本可以从直流母线电压及其电压变化率得到体现[10-12]。因此,本文将以直流母线电压及其电压变化率作为模糊控制器的输入量,通过模糊控制器实时地、平稳地调整功率变换器的开关管占空比,在保持直流母线电压稳定和平抑脉冲功率波动的同时,还能够有效提高储能系统的功率输出能力,优化蓄电池的工作环境。当负载以较低功率正常运行时,蓄电池作为主要电源供电,且几乎提供负载所需的全部能量,占空比稳定在初始水平保持不变。当负载发生波动导致功率大幅度增加时,应根据直流母线电压和电压变化率具体调节占空比以及占空比的增加速度。比如,当电压较低且电压变化率呈现比较大的下降趋势,这时应快速增加占空比;当电压稍低且电压变化率呈现缓慢的下降趋势时,应缓慢增加占空比。
2.1模糊规则建立
2.1.1输入量模糊化
输入模糊变量直流母线电压与给定的基准电压(DC48V)之差V以及V的变化率E。将V的值从小到大转换成对应的模糊子集为:{NBG,NSL,ZEO,PSL,PBG},隶属度函数采用三角形隶属度函数;E的值也从小到大转换成对应的模糊子集为:{NBG,NSL,ZEO,PSL,PBG},隶属度函数采用三角形隶属度函数。
2.1.2输出量模糊化
输出模糊变量:双向功率转换器的占空比D。将其值转换成对应的模糊子集为:{derease_vfast,derease_fast,decrease_slow,decrease_vslow,okay,increase_vslow,increase_slow,increase_fast,increase_vfast },隶属度函数采用三角形隶属度函数。
{NBG,NSL,ZEO,PSL,PBG}代表{负大,负小,零,正小,正大}。模糊控制规则表1所示。

表1 模糊控制规则表
2.2模糊推理:
每条模糊规则都对应一个模糊关系Ri,这25个模糊关系Ri(i=1,2,…25)的并,就是控制系统总的模糊关系R即:
(16)
近似推理总输出为:
(17)
或
(18)
上式中“∘”代表合成算法,A*为输入量矩阵形式,U*为输出量矩阵形式,A*=A*T。实际中一般使用式(18)作为计算公式,因为每次输入量不一定能全部激活所有的Ri,因此只算出被激活的控制规则Ri进行近似推理即可,这样可以大大减小计算量[7]。
2.3去模糊化
本文采用面积中心法。面积中心法就是先求出模糊集合隶属函数曲线在对应横坐标范围内的积分,即它们包围的面积,再求出这个面积中心的横坐标值,此值即为去模糊化后的精确值。设论域U上F集合A的隶属函数为:A(u),u∈U。中心的横坐标为uce,则按定义得:
(19)
3 仿真
图3为蓄电池—超级电容器混合储能系统的整体仿真结构图。
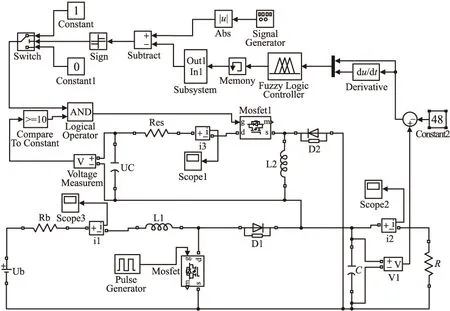
图3 仿真整体结构图
3.1构建脉冲宽度可调的脉冲发生器
在MATLAB/Simulink中,无现成的占空比可调的脉冲发生器模块,因此在仿真中需要自己搭建相关电路来构成。根据波形变换等相关原理,利用与目标脉冲相同频率的三角波与比较器可以实现此功能。
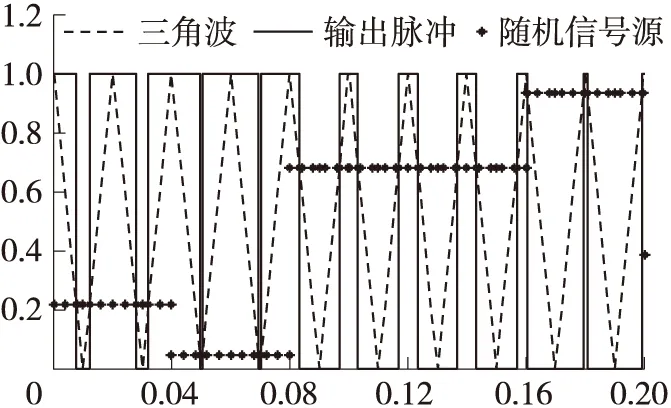
图4 随机信号激励下的脉冲图
图4为构建的脉冲发生器在随机源激励下的波形图。可以看出,输出脉冲的宽度随着随机信号源的变化而呈现线性变化,且其频率与三角波频率相同,可以满足仿真的需求。
3.2超级电容器-蓄电池混合储能系统仿真结果图及其分析
本系统蓄电池为12V/8Ah,内阻0.02Ω;超级电容器单体参数为1 800F/2.5V,最大内阻RES为1mΩ。设系统输出波动功率最高为5kW,持续时间为10s。采用功率法计算匹配方案。取理想情况K=1,超级电容器储能单元的实际输出效率为η=0.72,代入式(9)计算得m与n的积为15.545,取整数为16。将16只超级电容器串联成一条支路构成超级电容器组,其电压等级可达40V,等效RES为0.016Ω,等效电容为112.5F。超级电容器组的安全电压最低为10V,输出初始电压48V。占空比的设置由式(6)和(7)确定。直流母线电容值1F,电感L1为23μH,L2为125μH,开关频率f为10kHz,为方便仿真时间均设定为2s。
仿真分为充电过程和放电过程。充电过程中应主要考虑蓄电池充电电流的大小,以避免过电流充电导致蓄电池损坏。充电过程中只有蓄电池、Boost变换器以及超级电容器组处于工作状态。为匹配超级电器组单元的额定电压,据式(7)设定Boost变换器的占空比值。图5、图6分别为充电时的蓄电池电流图和超级电容器电流图。0到1s以40A电流正常给蓄电池充电,由图5可以看出蓄电池电流基本稳定;1s后充电电流突增为80A。从图6上看出,超级电容器组凭借其电流应力高、充电速度快的优点迅速吸收了突增的大电流,避免了大电流对蓄电池充电,延长了蓄电池的使用寿命,从而验证了基于2种直流功率变换器的蓄电池—超级电容器并联控制系统的模型是合理可行的。
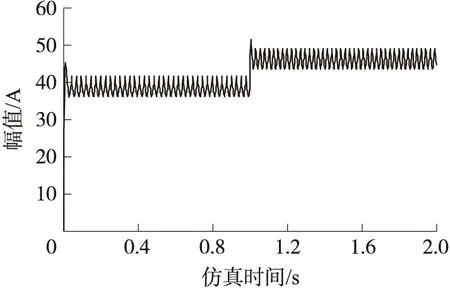
图5 蓄电池电流
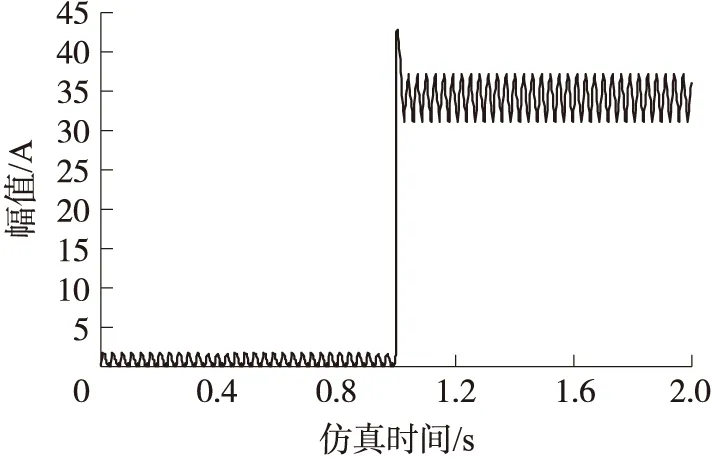
图6 超级电容器电流
图7~图10分别为充满电后放电过程中得到的负载电压图、负载电流图、蓄电池电流图及超级电容器电流图。负载从0到1s为10Ω,系统以低功率正常运行,可以看到蓄电池作为主要电源,几乎提供负载全部所需的能量。负载从1s后突变为1Ω,系统以比较高的功率运行。

图7 直流母线电压
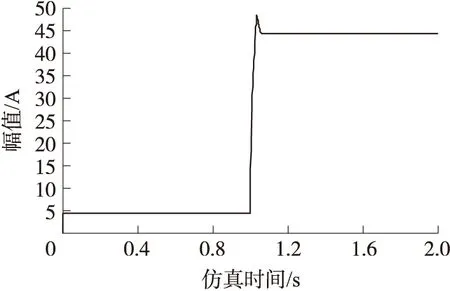
图8 负载电流
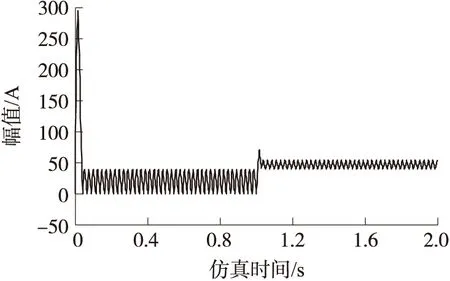
图9 蓄电池电流
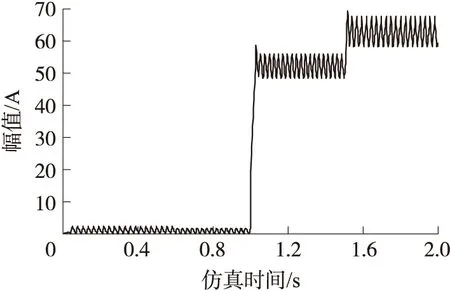
图10 超级电容器电流
由图7、图8可以看出,超级电容器组以很快的速度跟踪并迅速弥补功率突变瞬时所需的巨大功率,提供了将近所需总功率的2/3,避免了蓄电池大电流放电。尽管蓄电池在功率突变时电流也有小的波动,但时间很短。由于模糊控制器平滑地调节作用,蓄电池的电流很快稳定在一定范围,并且系统在发生功率波动时运行稳定,未出现系统振荡现象。约1.5s时,超级电容器组由于大功率放电,其储能一定程度减小,电压减小,经模糊控制器调节使其输出电压保持稳定,同时自身增加输出电流以保持原高功率输出。由图5、图6可以看出电压基本在45V左右波动,为标准目标电压的96%,负载电流也基本稳定,满足系统要求。其中损耗主要是由于系统内部内阻以及开关管损耗造成的,内阻损耗值可以由式(5)算得,约为0.67V,可见开关管的损耗还是比较大的。由上分析可以说明,混合储能系统在整个运行中基本稳定,采用模糊算法作为蓄电池—超级电容器混合储能系统的控制策略应是可行有效的。
4 结论
本文设计了基于Boost型和Buck-Boost型功率变换器的超级电容器—蓄电池并联控制系统,针对混合储能系统充放电过程具有非线性、时变性、滞后性的特点,提出了一种基于模糊算法的储能系统优化控制策略,并在MATLAB/simulink进行了建模和仿真。从仿真结果可以看出,通过模糊控制器实时地、平稳地调整功率变换器开关管占空比,混合储能系统运行稳定,直流母线电压基本保持恒定,在负载功率突增时不仅能够满足其功率需求,而且有效避免了蓄电池的大电流放电,从而优化蓄了电池的工作过程,由此表明模糊算法在混合系统控制上有着良好的效果。
参考文献:
[1]周林,黄勇,郭珂,等.微电网储能技术研究综述[J].电力系统保护与控制,2011,39(7):147-151.
[2]王晓峰,梁吉.碳纳米管超级电容器-锂离子电池复合电源在GSM移动通讯中的应用[J].电子器件,2004,7(4):547-551.
[3]张丹丹,罗曼,陈晨,等.超级电容器-电池复合脉冲电源系统的试验研究[J].中国电机工程学报,2007,27(30):26-31.
[4]刘建涛,张建成.一种超级电容器-蓄电池混合储能系统的控制方法[J].电力科学与工程,2011,27(1):1-4.
[5]戴咏喜,徐冲,刘以建.应用于脉冲负载的蓄电池和超级电容器混合储能的研究[J].通信电源技术,2011,28(4):12-14.
[6]林飞,杜欣.电力电子应用技术的MATLAB仿真[M].中国电力出版社,2008.
[7]张慧妍,齐智平.超级电容器储能单元的设计分析[J].电源技术,2006,30(4):322-325.
[8]石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,北京交通大学出版社,2008.
[9]丁丰平,张华强,苏振.基于预测控制的Fuzzy-PID控制算法研究[J].电子器件,2007,30(6):2152-2158.
[10]张坤,吴建东,毛承雄,等.基于模糊算法的风电储能系统的优化控制[J].电工技术学报,2012,27(10):235-241.
[11]李昕,曲梦可,荣誉.基于MSP430单片机模糊温湿度的控制器设计[J].传感技术学报,2007,20(4):805-808.
[12]乔兴宏,吴必军,王坤林,等.基于模糊控制的光伏发电系统MPPT[J].可再生能源,2008,26(5):13-16.
[13]张步涵,王云玲,曾杰.超级电容器储能技术及其应用[J].水电能源科学,2006,24(10):50-52.
[14]Huggins R A.Supercapacitors and Electrochemical Pulse Sources[J].Solid State Ionics,2000,134(1-2):179-195.
[15]Conway B E.Transition from“Supercapacitor”to“Battery”Behavior in Electrochemical Energy Storage[J].J.Electrochem Soc,1991,138(6):1539-1548.
[16]Spyker R L,Nelms R M.Classical Equivalent Circuit Parameters for a Double-Layer Capacitor[J].IEEE Trans on Aerospace and Electronic Systems,2000,36(3):829-836.

宋宏伟(1988-),男,硕士研究生,主要研究方向为电力电子设备的开发与研究,shwysl@ 163.com;

吕玉祥(1964-),男,教授,硕士生导师,主要从事电力电子设备的开发与研究,lyx823@126.com。
TheApplicationandSimulationofHybridEnergyStorageSystemBasedonFuzzyAlgorithm
SONGHongwei1,LVYuxiang1*,WANGQiyin2,ZHAORui2
(1.College of Physics and Optoelectronics,Taiyuan University Of Technology,Taiyuan 030024,China;2.State Grid Da Tong Power Supply Company,Datong Shanxi 037008,China)
Abstract:Parallel control system for battery-super capacitors is designed based on the two kinds of power converter.And a kind of energy storage system optimization control strategy based on fuzzy algorithm is also put forward for the characteristics of nonlinear,time-varying,hysteresis in the charge and discharge process of hybrid energy storage system.Then its modeling and simulation is finished in MATLAB/Simulink.Simulation.Experimental results show that with the new control strategy the power output of energy storage system is improved and stability of DC bus voltage is maintained.In addition,the disadvantages of oscillation produced easily in the traditional algorithm of control system is effectively improved and the working process of the storage batteries is optimized thatis good for extending its life.
Key words:hybrid energy storage;fuzzy algorithm;modeling and simulation;super capacitor;battery
doi:EEACC:8110B10.3969/j.issn.1005-9490.2014.05.035
中图分类号:TM53
文献标识码:A
文章编号:1005-9490(2014)05-0962-06
收稿日期:2013-09-26修改日期:2013-10-12

