粘滞阻尼减震结构最优极点配置与随机振动分析
杜永峰, 李春锋, 李 慧
(1.兰州理工大学 防震减灾研究所,兰州 730050;2.河西学院 土木工程学院, 甘肃 张掖 734000;3.西部土木工程防灾减灾教育部工程研究中心,兰州 730050)
粘滞阻尼器仅提高结构的阻尼而不改变刚度,具有在较宽频域范围内保持粘滞线性反应、环境温度不敏感、产生的阻尼力与位移异相、较好的可靠性和耐久性等特点,在土木工程结构减震控制设计与研究中得到了广泛的应用[2-7]。
鉴于建筑结构减震控制分析的多目标性,使得极点配置算法在结构减震控制设计与应用中的使用受到了一定程度的限制,文献[1]针对结构减震控制的多目标性,在考虑外界扰动的情况下对多目标情形下极点最优配置唯一性实现问题进行了研究,较好的处理了这一局限性,为该算法在土木工程行业的应用提供了一些帮助。然而文献[1]所得的控制力矩阵在物理意义上同LQR算法均表现出了控制力刚度不为零的现象,当结构减震控制使用粘滞阻尼器时,使得该算法的应用受到了限制。为克服文献[1]的不足,本文提出基于粘滞阻尼减震结构最优极点配置算法,以补充文献[1]算法的不足。
此外,由于结构减震控制中地震作用的不确定性,利用随机振动理论构造随机激励,并结合现有算法对最优极点配置前后粘滞阻尼减震结构进行随机振动分析,以此证明所提供最优极点配置算法的有效性与正确性,为实际工程的应用与相关科学研究提供一些帮助。
1 粘滞阻尼减震结构数学模型建立
1.1 线性震动微分方程的建立
地震下线性结构震动受控系统的微分方程为:
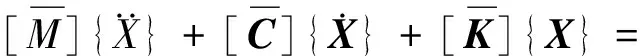
(1)

1.3 非线性震动微分方程建立及等效线性化
建筑结构在强震作用下处于弹塑性状态,表现出较强的非线性特性,其形式主要表现在结构阻尼项和刚度项或两者的组合,依据本文讨论,建立非线性震动微分方方程:
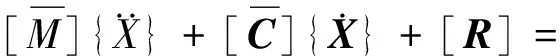
(2)
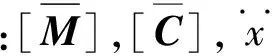
(3)
其中:vi为第i层的层间相对位移,vi=xi-xi-1,zi为第i层滞回位移,ki为第i层屈服前刚度,αi为第i层屈服后刚度与屈服前刚度之比,Ai,βi,γi,ni为滞回曲线的参数。
由此,可写出系统等效线性方程:
(4)
(5)
式中,[Ke]为弹性刚度矩阵,为αi与层剪切刚度乘积的矩阵转换,[Kh]为滞迟刚度矩阵,为(1-αi)与层剪切刚度乘积矩阵转换,实际计算时需特别注意X,V区别,[Ceqx]表达形式详见文献[8-9]。其中,[Ceqv]=diag([ceqi]),[Keq]=diag([keqi]),结构为混凝土结构时[10],可取Ai=1,ni=2,γi=-0.5(1-αi)/xy,xy为屈服强度与屈服前刚度比值,βi=-3γi。
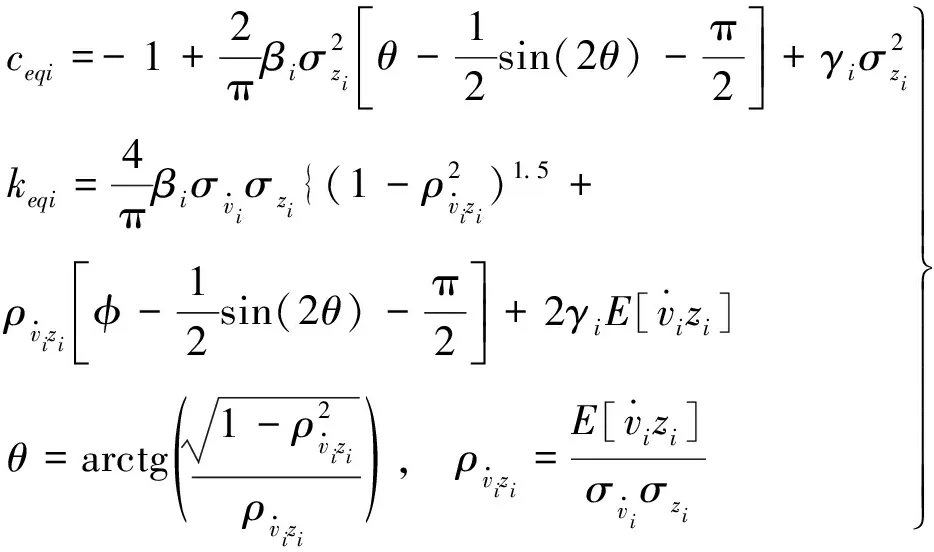
(6)
1.3 结构减震控制系统状态方程
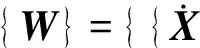
(7)
[A]为状态矩阵,[D]为输入矩阵,[C0]为单位阵,线性系统时自由度为2n,非线性系统时自由度数为3n。具体为:
当系统为线性系统时:
(8a)
当系统为弹塑形形态时:
(8b)
粘滞阻尼器可看作一种无刚度速度相关型阻尼器,依据能量相等原理进行等效线性化后的力学模型可表示为:
(9)
式(7)中,[G]=[0,Cd]为控制力反馈增益矩阵,其中[Cd]为等效粘滞阻尼系数矩阵。此处可与文献[1]对比发现:在粘滞阻尼控制下,结构刚度部分的矩阵系数全为0,这为进行振动控制算法研究提出了一些要求。
1.4 结构传递函数矩阵
由于传递函数矩阵是系统输入输出的描述,依据传递函数矩阵的不变性,在进行控制系统的零极点配置时有必要对地震下建筑结构震动控制系统的传递函数矩阵进行详细讨论。
(1) 地震下结构震动系统的输入输出模型
零初始条件下的未控系统输出输入关系可表示为:
{Y(s)}=[T(s)]{Xg(s)}=
[C0](s[I]-[A])-1[D]{Xg(s)}
(10)
式中,T(s)为未控系统传递函数矩阵,当输入地震扰动矩阵为一维向量时,具体可写为:
[T(s)]=[C0](s[I]-[A])-1[D]=
[g1,1(s)g2,1(s) …gq,1(s)]T
(11)
零初始条件下的受控系统输出输入关系可表示为:
{Y(s)}=[Tc(s)]{Xg(s)}=
[C0](s[I]-[A]+[B][G])-1[D]{Xg(s)}
(12)
(2) 传递函数矩阵讨论
为讨论零极点位置变化对结构振动控制系统的影响,以非控结构震动控制系统为例,将微分方程右端地震输入前负号并入地震波中,从而在地震作用作用下,传递函数矩阵为对角矩阵,其位移传递函数推导过程中如下:
(13)
(14)
地震作用下结构的位移传递函数为:
(15)
其中,D1=m1s2+(c1+c2)s+(k1+k2)
Di=mis2+(ci+ci+1)s+(ki+ki+1),(2≤i≤n-1)
Dn=mns2+cns+kn,Ni=cis+ki,(2≤i≤n)
上面各式中,mi,ci,ki为各楼层的层质量、层阻尼系数和层刚度。
此外,当结构体系的阻尼为瑞利阻尼[C]=a[M]+b[K]时,则有:
D1=m1s2+cR1s+(k1+k2),
cR1=αm1+β(k1+k2)
Di=mis2+cRis+(ki+ki+1),
cRi=αmi+β(ki+ki+1)
Dn=mns2+cRns+kn,
cRn=αmn+βkn
Ni=βki(s+1), (2≤i≤n-1),
Nn=βkn(s+1)
从上面的推导可以看出,当结构中施加粘滞阻尼控制器时,粘滞阻尼系数的增加将使结构的零极点发生很大的变化,结构的输入输出与结构零极点位置间存在较大依赖关系,为使结构在地震作用下的响应尽可能减小,进行最优极点配置是使其减小的一种内在措施。
2 粘滞阻尼结构最优极点配置
2.1 粘滞阻尼结构最优极点的确定
结构减震控制的主要目的是通过增大结构的阻尼以减小结构在地震作用下的响应。由于粘滞阻尼器可看作一种无刚度速度相关型阻尼器,粘滞阻尼减震结构在施加粘滞阻尼器的前后结构的自振周期不变,增加阻尼器后,结构体系的极点变化是在以非控结构自振频率ω为半径的圆周上移动,此外,系统阻尼值的增加主要通过极点在复平面内的移动来体现,极点距离虚轴越远,极点与原点连线矢量与负实轴的夹角越小,即系统阻尼越大(β2<β1),如图1所示,图中P1为未控系统某个极点,P2为P1在自振频率ω不变前提下沿圆周移动后目标极点,β1、β2及ω1、ω2分别为结构受控前后阻尼角和自振频率。具体有:
系统的极点常可表示为:
(16)
系统阻尼角:
βi=cos-1(ξi)
(17)
为获得具有工程意义的最优配置极点,观察式(16)、(17)及图1,假定P1为未控系统固有极点,P2为受控系统期望极点,可以得出:粘滞阻尼器的施加实际是使结构的极点沿原未控结构自振频率的圆周向远离复平面虚轴的方向移动,距离越远,结构体系阻尼越大。因此,在结构目标阻尼比一定的条件下,可通过极点在复平面的移动来实现最优(目标)极点的确定。
2.2 粘滞阻尼结构最优零点的确定
由1.4部分传递函数矩阵讨论可以发现:① 极点左移的同时,导致零点随之左移;② 零点移动的幅度随极点移动幅度确定,具体可参照极点平移确定。下面简要介绍其确定方法:
首先,根据式(7)确定未控系统的零点:
(18)
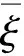
最后,依据确定的最优(或目标)零、极点构造传递函数阵。
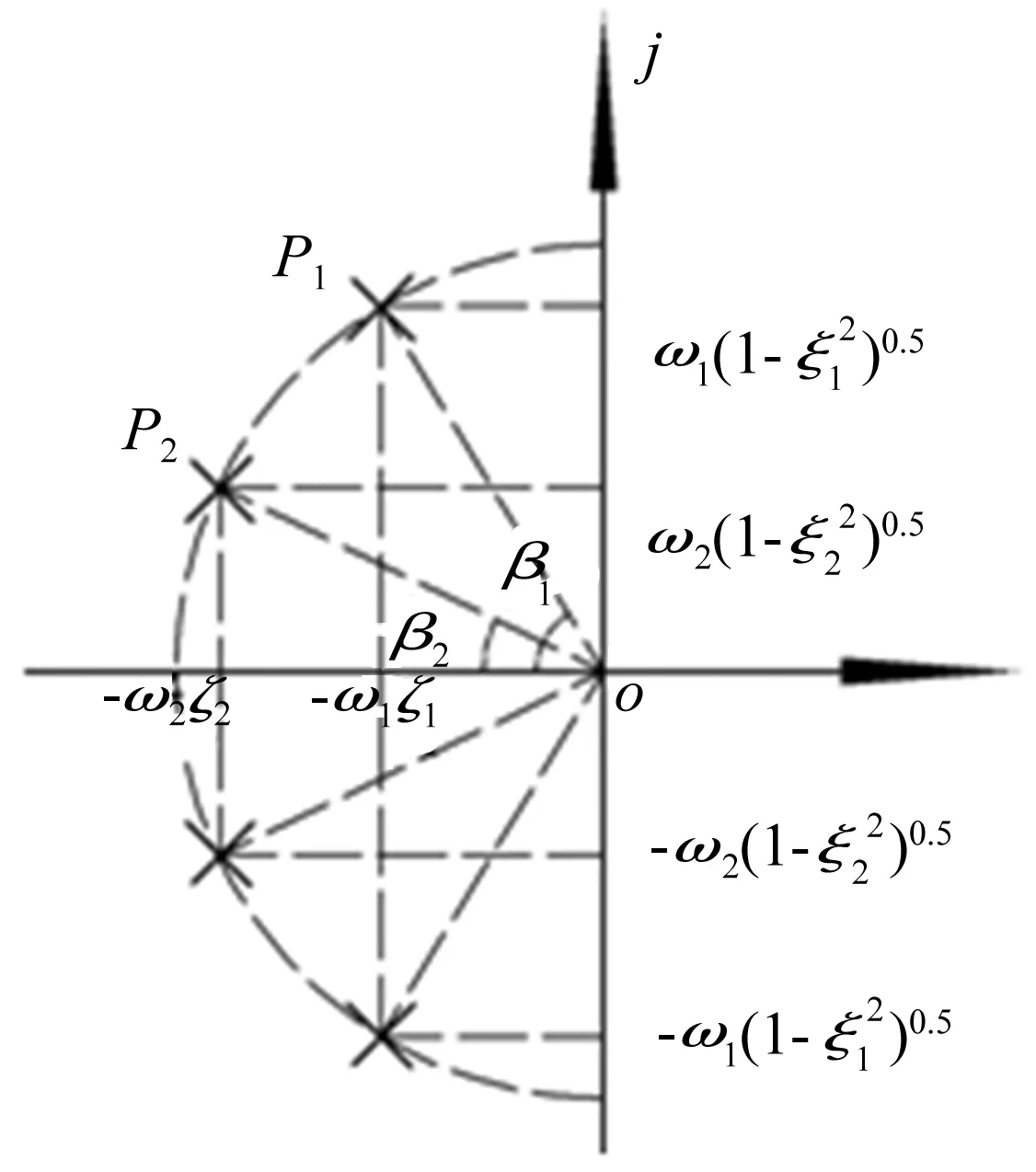
图1 复平面最优极点配置图
2.3 最优极点配置算法总结
针对上述最优(目标)极点确定及配置的思路,为条理性现将其总结如下:
(1) 对给定未控制系统,求取其传递函数矩阵,令式(15)传递函数矩阵中各子式分母、分子为零,求出零、极点;
(2) 根据(1)所得零、极点分布情况,由2.1, 2.2内容确定最优(期望)零、极点;
(3) 根据最优(期望)零、极点,求其在零输入下的传递函数矩阵[Gc];
(4) 针对获得的传递函数阵,确定系统状态方程的目标最小实现:∑(Ac,Bc,Cc,Dc);传递函数阵的实现读者可参考文献[1]提供的步骤进行。
3 结构随机振动分析
随机振动分析是计算结构体系动力可靠度的基础,减震结构在平稳随机地震作用下随机响应的计算步骤可归纳为:
令
(19)
式(7)的解设为:
{W}={H(ω)}eiωt
(20)
其次,将式(19)、式(20)代入式(7),则有:
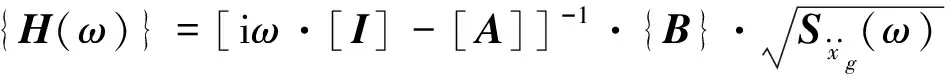
{W}={H(ω)}·eiωt=
(22)
最后,利用前述响应量,按式(22)计算自相关、互相关矩阵及对应统计量。

(23)
这里符号⊗表示两矩阵相乘产生一同阶矩阵。然后由式(23)可以很容易的利用下式求出其对应的方差值:
(24)
4 工程算例
4.1 工程应用举例
为验证本文结论的正确性,选用文献1给定的算例,结构各相关参数重新列些如下:结构层质量与层刚度分别为:mi=4×105kg,ki=2×108N/m(i=1,2,3),结构阻尼采用瑞利阻尼,前两阶振型的阻尼比ξ1=ξ2=5%,假定工程所在地的抗震设防烈度为8度,场地土较坚硬,属于《建筑抗震设计规范》(GB50011—2010)中Ⅰ1类第2组。
4.2 地震地面运动的加速度功率谱模型
为进行随机振动分析,采用Clough和Penzien建议的零均值平稳双过滤白噪声功率谱来描述地面运动,即地震动的单边功率谱可表达为:
(25)
其中,S0为基岩运动的白噪声单边功率谱强度,HkT(ω)为日本金井清-田治见宏建议的过滤器,Hcp(ω)为美国学者克拉夫-彭津提出低频过滤器。
(26)
(27)
其中,ωg为工程场地的卓越频率取ωg=20.94,ζg为场地的阻尼比ζg=0.64;ωc和ζc分别为低频过滤器的特征频率和阻尼比;取ωc=0.15ωg,ζc=ζg。推算小震作用下单边功率谱强度为:S0=2×5.247 5×10-4m-2·s-3,大震作用下单边功率谱强度为: S0=2×1.713 5×10-2m-2s-3,其输入的功率谱密度曲线见图2。图中左纵标表示小震幅值,右纵标表示大震幅值。
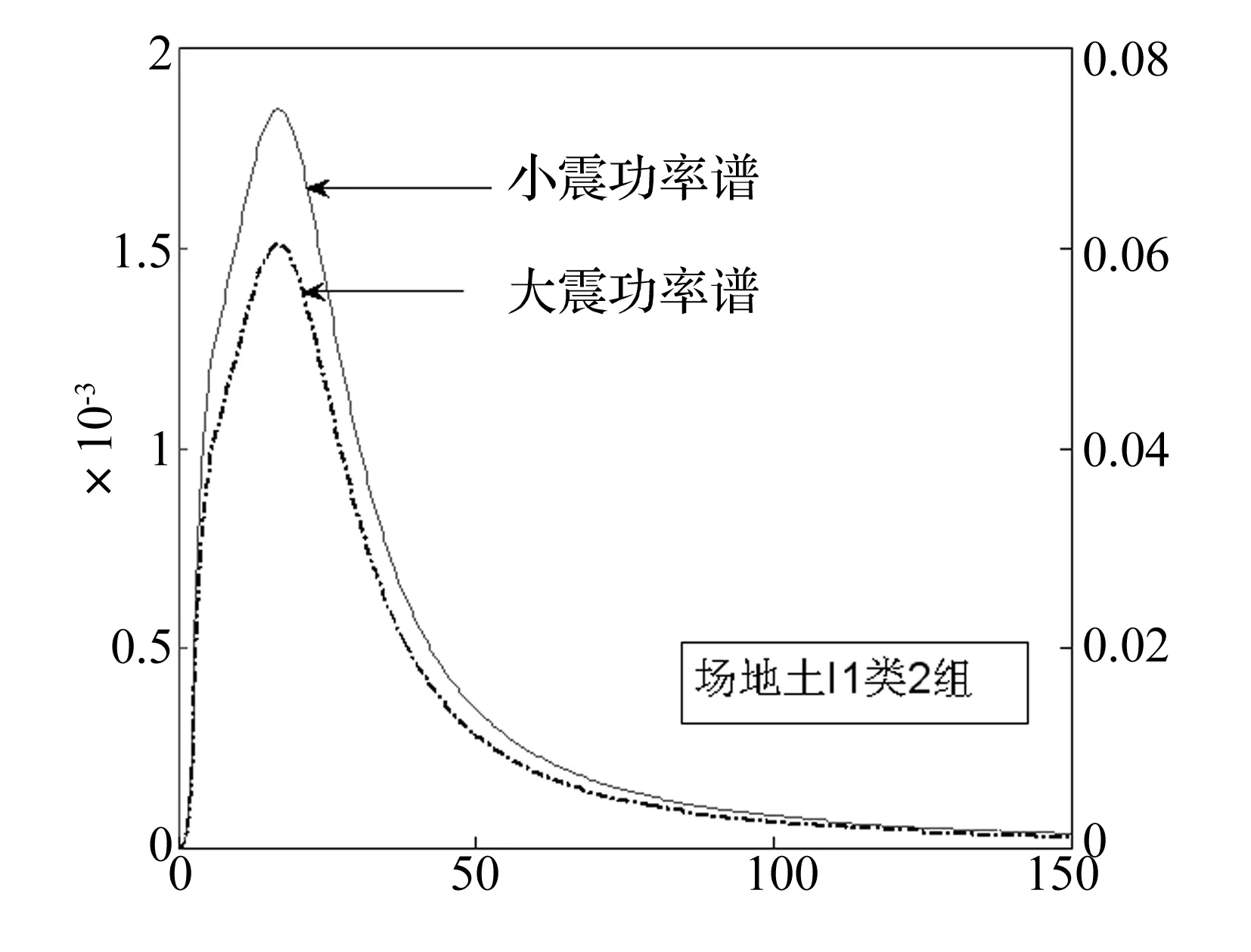
图2 场地土输入功率谱
4.3 随机响应分析
为便于讨论,仅列出本文算法与LQR算法所得的反馈增益矩阵,从中可以得出:由于粘滞阻尼减震结构仅改变结构的阻尼力而不改变结构的刚度,从而使反馈增益矩阵刚度分量部分的系数全为0,这是LQR算法无法实现的;从矩阵系数来看,采用本文算法提供的阻尼力矩阵与LQR算法提供阻尼力矩阵非常接近,读者可进一步根据反馈增益矩阵求得控制力矩阵BG进行验证。
(1) LQR算法所得的反馈增益矩阵:
(2) 本文算法所得反馈增益矩阵:
结构体系在地震作用下,无论是小震作用下的线性响应还是大震作用下的非线性响应(对非线性进行等效线性化),采用随机振动的虚拟激励法求得的位移均方差和速度均方差如表1所示,通过表1可以得出:LQR控制算法和基于最优极点配置的粘滞阻尼控制算都能使结构的随机响应得到较大程度的减小,且在两种控制算法下的响应均方差非常接近,最大差异约仅为2%,这主要是由于在较为恰当的Q和R选择下LQR算法设计的主动控制力主要以阻尼力的形式施加于结构上,但本文提出的最优极点配置下的粘滞阻尼算法的物理意义更明确,也更符合实际,从而也说明本文所提供分析理论的正确性和有效性。

表1 小震下结构随机响应
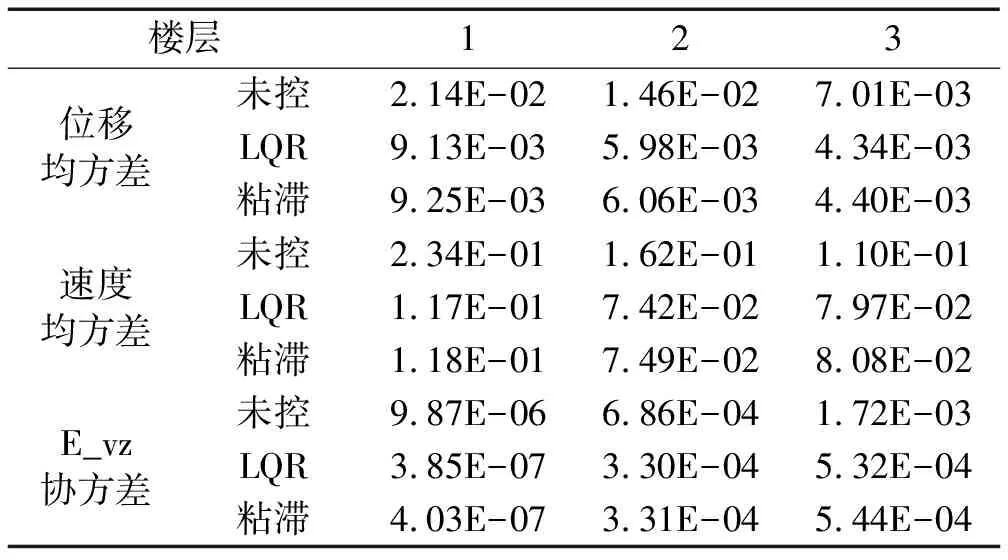
表2 大震下结构随机响应
5 结 论
粘滞阻尼减震结构在土木工程中的大量使用,使得阻尼控制器的最优配置为更多的学者和工程人员所关注,本文在文献1基础上对其内容做了进一步探讨。由于地震作用的不确定性,采用LQR最优控制算法和粘滞阻尼结构中的最优极点配置算法并结合随机振动理论对本文给定算例进行了详细讨论,具体结论为:
(1) 由于粘滞阻尼结构仅改变结构的阻尼力而不改变结构的刚度,为获得刚度系数为0的最优反馈增益矩阵,本文算法给予了较好的实现,这是LQR算法所不能实现的。
(2) 结合随机振动理论,对给定算例采用两种算法在大震、小震下进行随机振动分析,所得结果非常接近,从而验证了本文所提供算法的正确性和有效性。
[1]杜永峰, 李春锋, 李慧. 结构主动控制最优极点配置算法研究[J]. 振动与冲击, 2012, 31(19): 95-98.
DU Yong-feng, LI Chun-feng, LI Hui. Optimal pole assignment algorithm for structural active control [J]. Journal of Vibration and Shock, 2012, 31(19): 95-98.
[2]吴从晓, 周云, 邓雪松,等. 高位转换粘滞阻尼减震结构阻尼器合理阻尼系数研究[J]. 振动与冲击, 2011, 30(3): 180-184.
WU Cong-xiao, ZHOU Yun, DENG Xue-song, et al. Optimal damping coefficient of viscous damper in high-level transfer story structure [J]. Journal of Vibration and Shock, 2011, 30(3): 180-184.
[3]孙广俊, 李爱群.安装粘滞阻尼消能支撑结构随机地震反应分析[J].振动与冲击,2009,28(10):117-121.
SUN Guang-jun, LI Ai-qun. Random earthquake response analysis for an energy dissipation structure adding viscous dampers[J]. Journal of Vibration and Shock, 2009, 28(10):117-121.
[4]张微敬, 钱稼茹, 沈顺高,等. 北京A380机库采用粘滞阻尼器的减振控制分析[J]. 建筑结构学报, 2009, 30(2):1-7.
ZHANG Wei-jing,QIAN Jia-ru, SHEN Shun-gao,et al. Vibration reduction analyses of Beijing A380 hangar structure with viscous dampers[J]. Journal of Building Structures, 2009, 30(2):1-7.
[5]聂利英, 李建中, 胡世德,等. 任意荷载作用下液体粘滞阻尼器在桥梁工程中减震作用探讨[J]. 计算力学学报, 2007, 24(2):197-202.
NIE Li-ying, LI Jian-zhong, HU Shi-de, et al. Investigation of decreasing vibration effects of fluid viscous damper in bridge engineering under random loads[J]. Chinese Journal of Computational Mechanics, 2007, 24(2):197-202.
[6]邹银生, 陈敏, 冯承辉. 粘滞阻尼器消能减震结构的简化设计[J]. 湖南大学学报(自然科学版), 2005,32(6):1-5.
ZOU Yin-sheng, CHEN Min, FENG Cheng-hui. Simplified design method for energy dissipation systems using viscous dampers [J]. Journal of Hunan University (Natural Sciences), 2005,32(6):1-5.
[7]薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10.
XUE Su-duo, WANG Xue-sheng, CAO Zi. Parameters study on seismic randon model based on the new seismic code[J]. China Civil Engneering Journal, 2003,36(5): 5-10.
[8]林家浩,张亚辉. 随机振动的虚拟激励法[M].北京: 科学出版社,2004: 270-277.
[9]欧进萍, 王光远.结构随机振动[M]. 北京:高等教育出版社, 1998: 295-312.
[10]李桂青, 曹宏, 李秋胜, 等. 结构动力可靠性理论及其应用[M]. 北京:地震出版社,1993: 305-315.

