离心泵蜗壳内非定常流动特性

王松林，谭 磊，王玉川

(1. 华北水利水电大学 水利学院, 郑州 450011; 2. 清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084)

离心泵蜗壳的主要作用是汇聚流体，减小流体运动的圆周速度分量，进一步将流体的动能转化为压能，使其流动均匀地进入后续流道。离心泵蜗壳内流动状况对其运行特性具有重要影响[1-2]。康伟等[3]采用大涡模拟方法计算了离心泵蜗壳内非定常流动，结果发现常规的等速度矩的型线设计并不能获得完全等速度矩的流动，压水室径向断面上存在较强的二次流。张兄文等[4]对离心泵内部流动进行了数值研究，结果表明叶轮出口的射流-尾迹结构相对蜗壳不同位置而变化，蜗舌区射流-尾迹现象比蜗壳蜗型段中部更加明显。祝磊等[5]采用非定常数值模拟，分析了蜗舌结构对离心泵压力脉动和径向力的影响。朱荣生等[6]数值分析了1 000 MW核电站主泵压水室内部压力脉动特性。结果表明，设计工况下压水室压力脉动频率受叶轮转频影响，非设计工况下压水室压力脉动频率受叶轮转频和叶片通过频率共同影响。

离心泵空化对机组的运行稳定性影响重大，空化严重时产生的大量空泡在离心泵流道内堵塞将导致扬程和效率的急剧下降，使其不能正常运行。

空化流动数值模拟基本分为界面追踪法和界面捕获法两类，其中又以界面捕获法中的均相流模型应用最广，在均相流假设下，空化模型可分为空泡动力学模型、状态方程模型和输运方程模型等三类[7-10]。Coutier-Delgosha等[11]通过数值模拟和试验测量研究了叶轮内部空化的类型和空泡结构的空间分布。王勇等[12]基于Rayleigh-Plesset空化模型数值模拟得到的离心泵叶片载荷在头部附近出现极小值，随着空化发展叶片载荷逐渐增大。杨敏官等[13]对离心泵临界空化点进行了非定常数值模拟，结果表明蜗舌附近压力脉动幅值在叶片通过频率下最大，随着叶轮内空化发展，其压力脉动幅值逐渐增大。

目前，离心泵内部非定常流动特性研究大多集中在叶轮区，而空化流动特性研究大多为定常工况，离心泵非定常空化流动下蜗壳内流动特性研究很少。基于修正的RNGk-ε湍流模型和输运方程空化模型，数值模拟了小流量工况下离心泵内部空化流动，分析了离心泵蜗壳内非空化和空化工况时压力脉动频域和幅值特征，为离心泵的稳定运行提供参考。

1 数值模拟方法

1.1 基本方程

流体运动基本控制方程为基于Reynolds平均的Navier-Stokes方程。

(1)

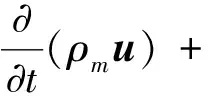
·[(μm+μt)[(μm+μt)·u]

(2)

式中，t为时间，ρm为混合相的密度，μt为湍流粘性系数，μm为动力粘性系数，按汽、液两相体积分数加权平均后得到，p为压力，u为速度矢量。采用RNGk-ε双方程湍流模型封闭控制方程组，RNGk-ε双方程湍流模型考虑了平均流动中的旋转情况，能够更为准确地处理高应变率及流线弯曲程度较大的流动，在水力机械中应用广泛[14-17]。考虑空化流动可压缩性的影响，引入密度函数f(ρm)对湍流粘性系数μt进行修正[18-19]：

(3)

f(ρm)=ρv+

[(ρm-ρv)/(ρl-ρv)]n·(ρl-ρv)

(4)

式中，k为湍动能,ε为湍流耗散率，cμ为经验常数0.845，ρl为液体密度，取值1 000 kg/m3，ρv为气体密度，取值0.554 kg/m3，n为常数，当n取适当值时，可有效减小混合物的湍流粘性系数，为较好地模拟离心泵内部空化流动，本文计算中取n=10[18-19]。

1.2 空化模型

空化模型采用基于Rayleigh-Plesset方程推导出的输运方程，考虑气泡的汽化和凝结过程，可得质量输运方程为：

(5)

(6)

(7)

式中，m+、m-为单位体积的质量蒸发速率和质量凝结速率。Cvap为蒸发项经验系数，取值50，Ccond为凝结项经验系数，取值0.01，αv为气相体积分数，Rb为气泡半径，取值10-6m，pv为汽化压力，取值3 540 Pa。

考虑湍流压力脉动对汽化压力的影响，修正后汽化压力为：

pv=psat+0.195ρmk

(8)

式中，psat为对应温度下饱和压力。

1.3 离心泵参数及网格

离心泵基本参数为：流量Qd=340 m3/h，扬程H=30 m，转速n=1 450 r/min，叶轮叶片数Zi=6。本文选取小流量工况Q=260 m3/h进行数值模拟。

离心泵全流道计算域由进口段、叶轮区、蜗壳组成[1]，全部采用结构化网格，并对叶片表面和蜗舌附近进行局部加密，蜗舌区局部网格如图1所示。

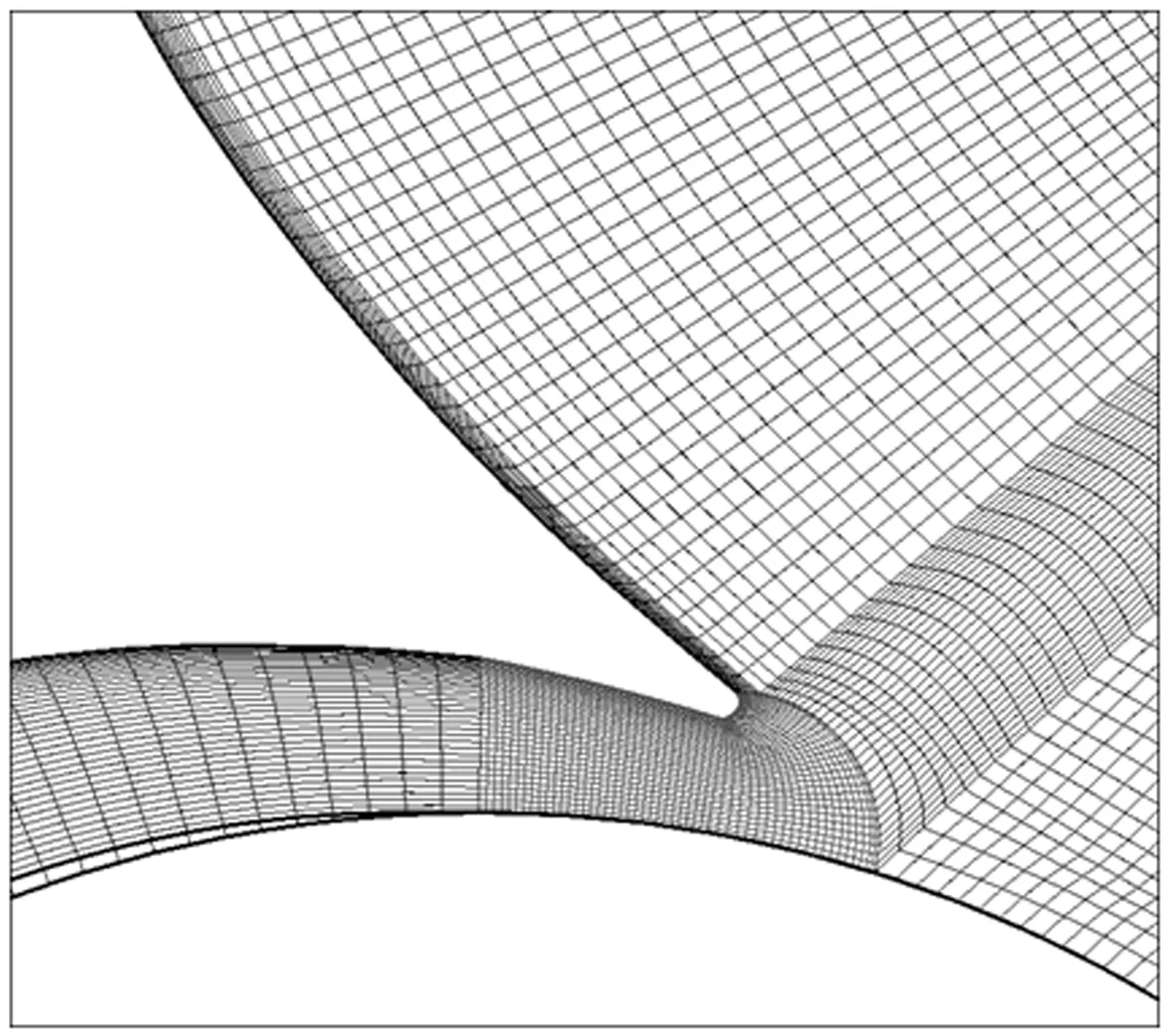
图1 离心泵蜗舌区局部网格

为验证网格无关性，对离心泵全流道计算域5组不同数量网格进行数值计算，结果显示当网格数大于180万时，离心泵扬程和效率变化很小，因此本文计算域网格数选为180万。在离心泵蜗壳内布置5个监测点，从蜗舌起沿流动方向依次为V1、V2、V3、V4、V5，如图2所示。

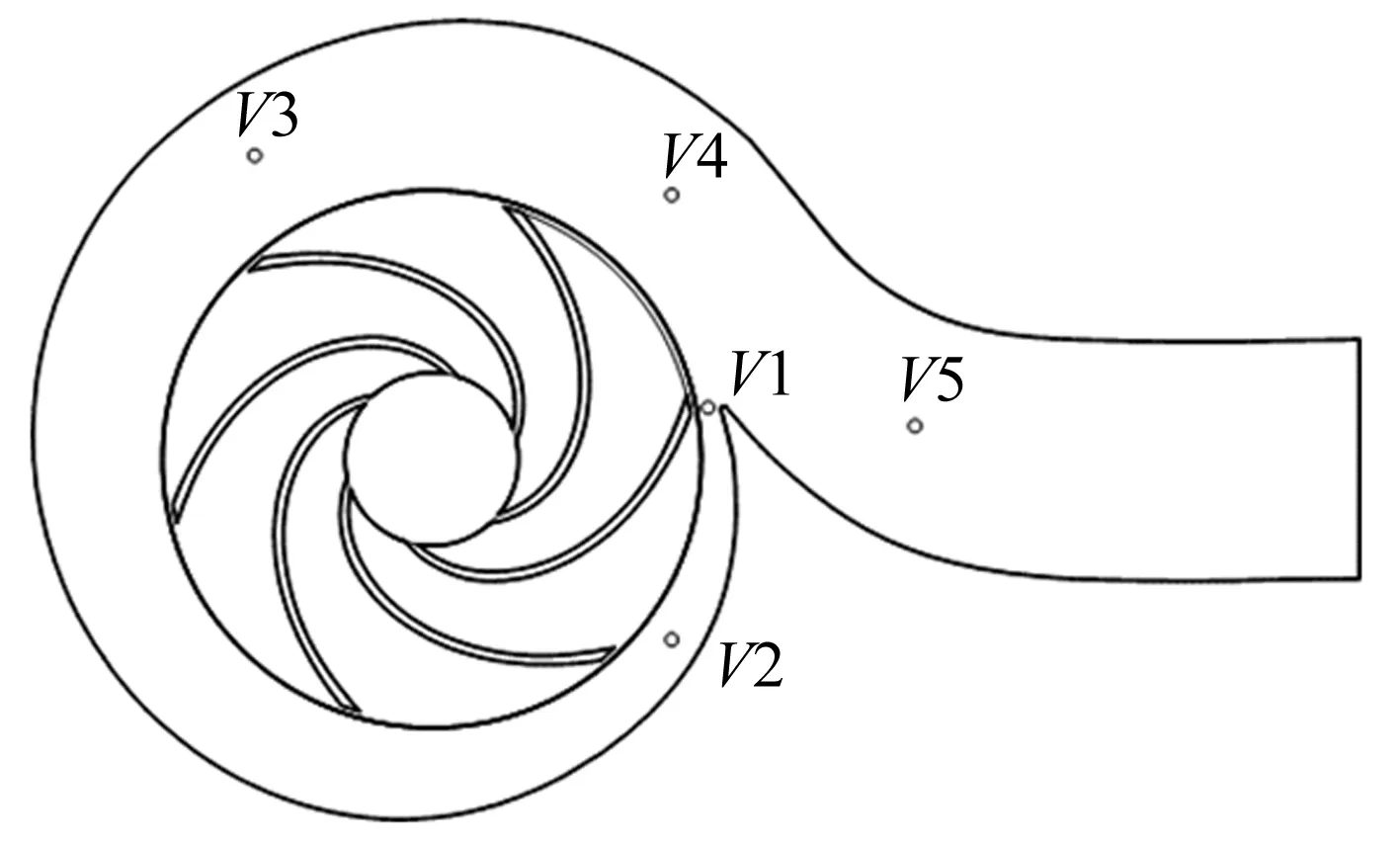
图2 蜗壳内监测点

1.4 计算方法

离心泵数值模拟采用计算流体力学软件CFX，进口给定压力，出口给定流量，固体壁面为不可滑移边界。定常计算中，进口压力值由试验测量值给定，并逐步降低，当前工况计算结果为下一工况初始值。非定常计算中，以定常计算的结果作为初始值。

离心泵叶轮旋转一周时间记为T。非定常计算中，时间步长为两个相邻叶片转过同一位置的间隔内取32个计算点，对应Δt=T/6/32=0.000 215 5 s，每个时间步长内迭代30次。为验证时间无关性，取三个不同时间步长进行计算，如图3所示，三个时间步长的计算结果差别很小，本文取Δt=0.000 215 5 s。

图3 时间无关性验证

2 数值模拟结果及分析

2.1 离心泵空化外特性

离心泵的有效空化余量NPSHA(Net Positive Suction Head Available)定义为离心泵进口断面单位流体的能量与汽化压力之差：

(9)

式中，pin、uin为离心泵进口处的压力和速度。

图4给出了离心泵扬程随有效空化余量的变化曲线。数值模拟结果与试验测量结果吻合较好，能较为准确地预测离心泵在空化临界点的扬程突降过程，验证了离心泵空化流动数值模拟方法的准确性。

图4 离心泵空化时扬程的变化

2.2 蜗壳内压力脉动频域

离心泵内部非定常流动数值模拟选择了3个工况点：① 非空化工况；② 临界空化工况NPSHA=2.2 m；③ 充分发展空化工况NPSHA=1.5 m。离心泵非定常流动数值模拟的总时间为10个叶轮周期，对5个监测点的压力脉动进行快速傅里叶变换(FFT)得到频域特性。由叶轮转速可知叶片通过频率(Blade Pass Frequency)为fBPF=145 Hz。

图5为蜗壳内5个监测点的压力脉动频域。图5(a)对应非空化工况，V1-V5监测点的压力脉动主频依次为2fBPF、fBPF、fBPF、fBPF、2fBPF，各点振幅在频率2fBPF以上均远小于主频幅值。图5(b)对应空化工况NPSHA=2.2 m，V1-V5监测点的压力脉动主频依次为2fBPF、fBPF、fBPF、fBPF、2fBPF。图5(c)对应空化工况NPSHA=1.5 m，V1-V5监测点的压力脉动主频依次为9.6 Hz、fBPF、9.6 Hz、9.6 Hz、9.6 Hz。在空化充分发展工况下，离心泵蜗壳内监测点的压力脉动主频非常低，这可能与离心泵内部空泡脱落、溃灭对流动的阻塞和扰动有关。

2.3 蜗壳内压力脉动幅值

表1为离心泵非空化、空化时蜗壳内5个监测点压力脉动的最大幅值。非空化工况下，蜗壳内压力脉动最大幅值在第2断面附近的V2处最大，蜗舌处V1其次，最小值在V3处。空化工况NPSHA=2.2 m时，V1、V3、V4、V5的压力脉动最大幅值与非空化时变化不大，而V2点的变化较为明显，约为非空化时的1.2倍。空化工况NPSHA=1.5 m，各点的压力脉动最大幅值均明显增大，V3、V4、V5的压力脉动最大幅值约为非空化时的2.0倍，V2点的压力脉动最大幅值远大于其他点。

2.4 蜗壳内压力分布

离心泵蜗壳内，蜗舌为蜗型段和扩散段的分隔点，流体经此处同时进入蜗型段和扩散段，流动状况非常复杂。据此，蜗舌附近V1的压力脉动应非常强烈，但是图5的结果显示，V2的压力脉动最大幅值远比V1大。

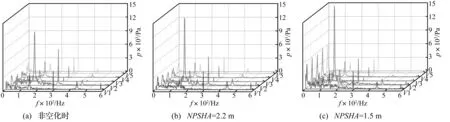
图5 蜗壳内压力脉动频域

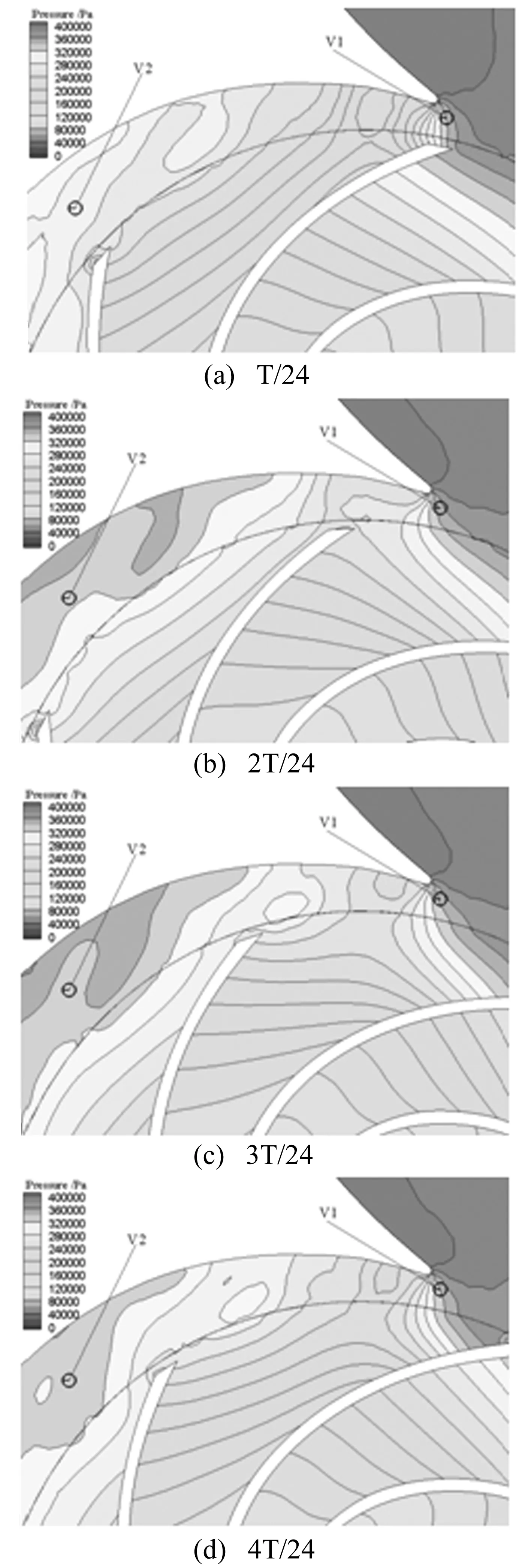
图6 蜗舌附近瞬态压力分布

表1 蜗壳内压力脉动的最大幅值

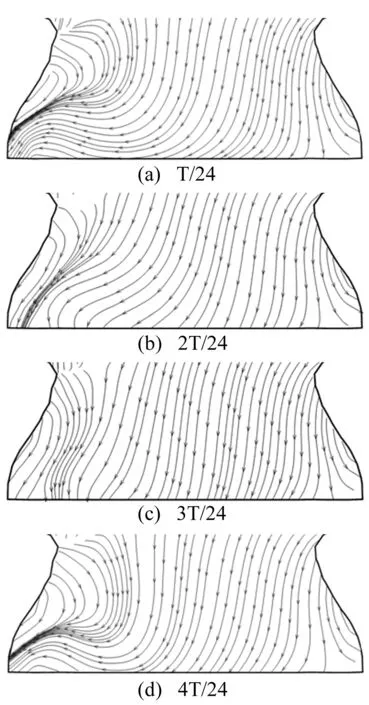
图7 V1横截面瞬态流线分布

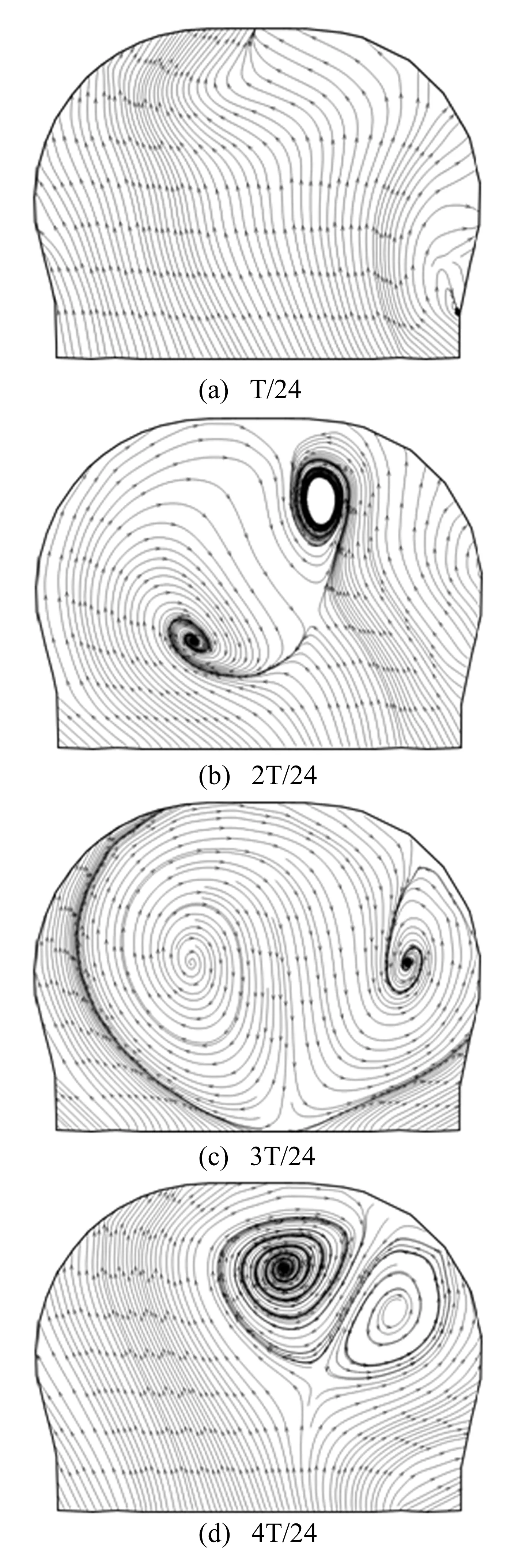
图8 V2横截面瞬态流线分布

为研究这一现象，图6给出了叶高中间面上，V1 和V2附近区域不同时刻的压力分布图。由图可知，叶高中间面上，V1处的压力梯度较大，而V2处压力梯度较小，但两者的压力分布在不同时刻变化不大。因此，叶高中间面上的压力分布图尚不足以解释上述现象。

为进一步研究上述现象，图7和图8给出了V1 和V2在蜗壳横截面上4个不同时刻的流线分布图。

由图7可知，蜗舌附近V1横截面上流态总体较为平顺，仅在左下角位置(对应离心泵出口一侧)出现局部扰动，流场分布不均匀。流场分布随时间变化不大。

由图8可知，V2横截面上流态则较为复杂。T/24时刻，横截面上流动较为均匀，右下角位置出现范围很小的顺时针旋涡，对周围有限范围内流动产生影响。2T/24时刻，横截面内存在明显的二次流，出现了两个非对称反向旋涡，两个旋涡强度不等，涡心分别位于横截面左下和右上位置。3T/24时刻，两个非对称反向旋涡的强度都有所减弱，左侧旋涡向上偏移，右侧旋涡向下偏移，横截面中间流线分布相对均匀。4T/24时刻，左侧旋涡强度增强，往中间位置发展，右侧旋涡紧邻之，强度较弱，横截面左半部分流线分布相对均匀。两个非对称反向旋涡的涡心位置、形状、强度随时间不断变化，是引起蜗壳内压力脉动和泵体振动的重要原因。

3 结 论

(1) 采用密度函数修正了RNGk-ε湍流模型，考虑压力脉动修正了输运方程空化模型，数值模拟了离心泵全流道空化流动，数值模拟结果与试验测量结果吻合较好，验证了计算模型和数值方法的准确性。

(2) 离心泵非定常流动中，非空化工况、空化工况NPSHA=2.2 m，V1-V5监测点的压力脉动主频为fBPF或2fBPF。而在空化工况NPSHA=1.5 m，V1-V5监测点的压力脉动主频为fBPF或9.6 Hz，离心泵内部空化充分发展时，空泡脱落、溃灭对流动的阻塞和扰动，是诱导低频压力脉动的可能原因。

(3) 离心泵非定常流动中，总体而言，空化时的压力脉动最大幅值大于非空化时。非空化和2个空化工况下，压力脉动最大幅值在蜗壳内第2断面附近的V2处最大。主要原因是蜗壳内V2横截面上内存在明显的二次流，出现了两个非对称反向旋涡，其涡心位置、形状、强度随时间不断变化，导致此处压力脉动幅值最大。

[1]王松林, 谭磊, 王玉川. 离心泵瞬态空化流动及压力脉动特性[J]. 振动与冲击, 2013, 32(22): 168-172.

WANG Song-lin, TAN Lei, WANG Yu-chuan. Characteristics of transient cavitation flow and pressure fluctuation for centrifugal pump[J]. Journal of Vibration and Shock, 2013, 32(22): 168-172.

[2]蒋爱华, 章艺, 靳思宇, 等. 离心泵流体激励力的研究: 蜗壳部分[J]. 振动与冲击, 2012, 31(4): 60-66.

JIANG Ai-hua, ZHANG Yi, JIN Si-yu, et al. Fluid exciting forces on centrifugual pump part Ⅰ: force on volute[J]. Journal of Vibration and Shock, 2012, 31(4): 60-66.

[3]康伟, 祝宝山, 曹树良. 离心泵螺旋形压水室内流场的大涡模拟[J]. 农业机械学报, 2006, 37(7): 62-65.

KANG Wei, ZHU Bao-shan, CAO Shu-liang. Large Eddy Simulation of the Flow through the Spiral Casing of a Centrifugal Pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(7): 62-65.

[4]张兄文, 李国君, 李军. 离心泵蜗壳内部非定常流动的数值模拟[J]. 农业机械学报, 2006, 37(6): 63-68.

ZHANG Xiong-wen, LI Guo-jun, LI Jun. Numerical simulation of unsteady flow in centrifugal pump volute[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(6): 63-68.

[5]祝磊, 袁寿其, 袁建平, 等. 不同型式隔舌离心泵动静干涉作用的数值模拟[J]. 农业工程学报, 2011, 27(10): 50-55.

ZHU Lei, YUAN Shou-qi, YUAN Jian-ping, et al. Numerical simulation for rotor-stator interaction of centrifugal pump with different tongues [J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(10): 50-55.

[6]朱荣生, 李小龙, 袁寿其,等. 1 000 MW 级核主泵压水室出口压力脉动[J]. 排灌机械工程学报, 2012, 30(4): 395-400.

ZHU Rong-sheng, LI Xiao-long, YUAN Shou-qi, et al. Collector discharge pressure fluctuation of 1 000 MW nuclear reactor coolant pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 395-400.

[7]Delannoy Y, Kueny J L. Two phase flow approach in unsteady cavitation modelling[J]. Cavitation and Multiphase Flow Forum ASME-FED, 1990, 98:153-160.

[8]Kubota A K, Kato H, Yamaguchi H. A new modelling of cavitating flows: a numerical study of unsteady cavitation on a hydrofoil section[J]. J. Fluid Mech, 1992, 240(1): 59-96.

[9]Merkle C L, Feng J, Peo B. Computational modelling of the dynamics of sheet cavitation[C]. 3rd International Symposium on Cavitation, Grenoble, France: 1998.

[10]Kunz R F, Boger D A, Stinebring D R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]. Computers & Fluids, 2000, 29: 849-875.

[11]Coutier-Delgosha O, Fortes-Patella R, Reboud J, et al. Experimental and numerical studies in a centrifugal pump with two-dimensional curved blades in cavitating condition[J]. Journal of fluids Engineering, 2003, 125: 970-978.

[12]王勇, 刘厚林, 袁寿其, 等. 离心泵内部空化特性的CFD模拟[J]. 排灌机械工程学报, 2011, 29(2): 99-103.

WANG Yong, LIU Hou-lin, YUAN Shou-qi, et al. CFD simulation on cavitation characteristics in centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(2): 99-103.

[13]杨敏官, 孙鑫恺, 高波, 等. 离心泵内部非定常空化流动特征的数值分析[J]. 江苏大学学报, 2012, 33(4): 408-413.

YANG Min-guan, SUN Xin-kai, GAO Bo, et al. Numerical analysis of unsteady cavitating flow characteristic in centrifugal pump[J]. Journal of Jiangsu University(Natural science edition), 2012, 33(4): 408-413.

[14]Yakhot V, Orszag S, Thangam S, et al. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids A, 1992, 4(7): 1510-1520.

[15]Liu Shu-hong, Li Sheng-cai, Wu Yu-lin. Pressure fluctuation prediction of a model kaplan turbine by unsteady turbulent flow simulation[J]. Journal of Fluids Engineering, 2009, 131: 101102-1-9.

[16]谭磊, 曹树良, 桂绍波, 等. 带有前置导叶离心泵空化性能的试验及数值模拟[J]. 机械工程学报, 2010, 46(18): 177-182.

TAN Lei, CAO Shu-liang, GUI Shao-bo, et al. Experiment and numerical simulation of cavitation performance for centrifugal pump with inlet guide vane[J]. Journal of Mechanical Engineering, 2010, 46(18): 177-182.

[17]Tan Lei, Cao Shu-liang, Wang Yu-ming, et al. Direct and inverse iterative design method for centrifugal pump impellers[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2012, 226(6): 764-775.

[18]Coutier-Delgosha O, Fortes-Patella R, Reboud J. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J]. Journal of fluids Engineering, 2003, 125: 38-45.

[19]Tan Lei, Cao Shu-liang, Wang Yu-ming, et al. Numerical simulation of cavitation in a centrifugal pump at low flow rate[J]. Chinese Physics Letters, 2012, 29(1): 014702.