数学新教材中的困惑

王亚丽

从教二十一年的我，深感现行数学教材内容较前期的确有所变化，在万变不离其踪的前提下，很有实用价值的知识点还是那样执着的被我们传授，值得欣慰的是，还不同程度地增加了好多与生活紧密联系的常规知识，同样在执教者精心策划与多样化教学手段的指引下淋漓尽致地展示给了学生，但作为我心里还是有点困惑。

一、内容编排宽泛化

教材打破了旧版的局限性，解方程的方法就是特例，经过了解，应用等式的基本性质解方程是为了和初中知识点接轨，虽然在强行灌输的基础上，学生从思想与行动中已默认，但课本只局限性的对形如：aⅹ±b=c、aⅹ×b=c、a+bⅹ=c， a×bⅹ=c讲述了利用等式的基本性质如何去解决，而对形如a-bⅹ=c及a÷bⅹ=c如何用等式的基本性质去解决却毫无说明，导致对有些资料中遇到此类问题难以解决的困惑，更为甚者是考试还出现同类问题，使得失分率比以前提升了15﹪。此外，五年级上册第六单元统计与可能性中新增了数学概念“中位数”，它从概念上来说虽不受偏大或偏小数据的影响，但它只能代表全体数据的一般水平：今年又在小学五年级数学下册第六单元统计一章节添置了“众数”， 一般来说，一组数据中，出现次数最多的数就叫这组数据的众数： 加之以前的“平均数”，三者既有联系更有细微的区别，迫使我遇到具体问题都难以定陀，从而使我深感到数学知识的可塑性更令人神往。特别每册书的最后一章“数学广角”很有趣味性，能把学生带到生活中感受数学的存在，了解到好多生活常识。例如：五年级下册数学123页的“生活中的数学”就让学生很容易的理解商场“均码”的含义，它就注重了平均数与众数的参与。相应的也为我们提供了好多方案性知识。例如：“打电话”一节，虽然学生理解起来很吃力，但作为执教的我来说，很有必要让学生从理性上了解此知识点，也使学生认识到打电话的实效性…。

二、实用价值可疑性

从编排角度谈教材很值得我们去挖掘，但有些知识点应用到生活中时我们就觉得理想化了，有点脱离实际的感觉，困惑随之而生。例如：在“打电话”一节，让给老师设计一个打电话的方案，尽快的让老师把紧急会议传达给每个学生，我想即使把方案设计的点滴不漏，老师第一分钟准时的传达给方案中的第一个接到通知的学生，但并非在第二分钟老师就会和第一个学生准时的传达给另外两个同学，也许在这个过程中老师和第一个同学同时传达给同一个人，这样的可能性随时会出现，还有，不一定就能万无一失的按方案顺利的进行下去，可见打电话的方案就显得有点古板，逊色。即使我们师生提前都设计了同一个方案，但不外乎保证每个同学都把方案随身携带，所以我觉得打电话就是一种理想化的教学，实用性很微妙。此外，在数学广角里找次品，虽然是很有趣的推理知识，帮助部分学生提高了辨析意识，能很快的用箭头示意图分析出问题，使人一目了然。但还存在值得谈讨的知识点—“天平”的实用价值，记得天平只是用来测量微小物体重量的，而我们把它始终出现在数学广角一节，还要用它找十瓶矿泉水中比较重的一瓶盐水，还有五年级数学下册练习二十六一题的十筐松果中较轻的一筐，在找的过程中我们都要把它分成（3、 3、 4），先把等数量的放上天平，难道三筐松果能被天平撑得住？虽然都说“如果”，但我的学生很值得我欣慰，个别聪明的学生就发问：“老师，天平不是很精密仪器吗？怎能用它测量如此有份量的物体…”。由此看来，学以致用要有原则性。

三、数学术语严密性

问题就在数学广角一节，教材中的练习题语言组织都很严密，问“至少称几次才能保证找出次品来”，学生很容易理解，但知识随时可变，练习册67页的3题，“如果用天平称，最少称几次就能找到11桶薯片中较轻的一桶”，有一个学生很有主见的说：“一次”，当时我也很纳闷，后来她说出自己的见解，因题中没“保证”二字，所以也许我一次就能找到。此外，学生质问：“最少，至少”在何种场合下是等同概念，我的解释，如果纯粹说“最少，至少”，他们是等同的，但“至少”后携带“保证”，“才能“二字就有所变化，例如：练习册67页4题的两个小题都问“至少称几次才能找出次品的糖果来”， 这样学生就潜意识的明白何种情况下并非一次就能找到次品。还有“倍”的概念，在教学因数与倍数一章节时，课本再三叮嘱是在整数范围内研究的，学生在学中理解透彻，但本学期第一章接触到分数乘法时，分数乘整数的两种意义，无可疑虑的能理解。可惜遇到分数乘分数的意义，课本显示“就是求一个数的几分之几是多少。”而令我担忧的是有关资料出现为：“是求一个数的几分之几倍是多少，还有换位的说法，例：1/2×3/4的意义即可说成是求 1/2的3/4是多少、也可以说成是求3/4的1/2是多少，”殊不知这样的说法对与错，搞得我也无所适从。

四、拓展延伸简单化

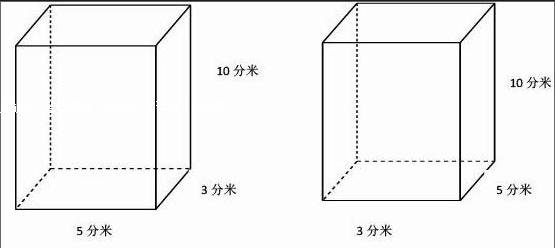
五年级数学下册第三单元长方体和正方体表面积计算一节，老师都费尽心机利用一切可观的实效教具，通过演示，面面俱到的把知识传授给了孩子们，同时认真的解决了每道练习题，可那些题型只属于浮浅型。虽然练习六的10、11题属于思维拓展型，但可塑性还算过得去，只要用教具真切的演示，接受者就会一目了然，说明课本知识拓展还不够深。从而导致部分学生接触教辅资料时就被一些“粘一起”表面积会怎样？“切开”表面积又会怎样的问题拦住了。课本虽没专题研讨，可我们教者必须把它作为重点知识去传授，否则遗留问题就会随之而来，这样导致教学任务明显的滞后化。“粘”还必须从三个角度一一说明、“切”也得从“纵切”、“横切”去探讨，“纵切”更要说明是沿哪个面去切，否则增加的面就不同，会引起原来长方体的长，宽数据发生变化。例如：一个高为10分米的长方体木块，如果纵向切成两个长方体后，表面积就增加60平方分米，如果横向切成两个长方体后，表面积就增加30平方分米。这个长方体的表面积是多少？

虽然怎么纵切最终算出长方体的表面积没发生变化，但对辨析能力不够强的同学在计算原来长方体长和宽时理解就更加吃力。

总之，在数学课堂教学中，我们虽然在新课标教学的指引下按部就班的完成任务，但作为执教者也要用心挖其掘中的困惑，衷心的摆揭与众，以便探讨。endprint