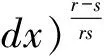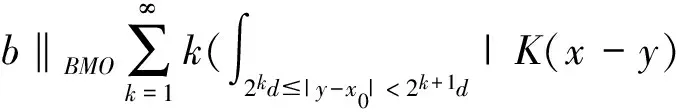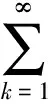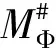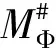一类满足örmander条件的奇异积分算子交换子的Lp有界性
曹 美 阳
(江西师范大学数学与信息科学学院,江西 南昌 332200)
曹 美 阳
(江西师范大学数学与信息科学学院,江西 南昌 332200)

交换子;奇异积分算子;sharp极大函数
1 引言和主要结果
奇异积分算子及其交换子的有界性在调和分析和偏微分中有重要的应用。在文献[1,2]中,Coifman和Janson等分别证明了由奇异积分算子和BMO函数生成的交换子在Lp(Rn)(1 定义1:设函数K∈L2(Rn)。存在常数C0>0使得: (2)|K(x)|≤C|x|-n; 文献[5,6]中考虑了一类变形的Hörmander的条件,并且得到相应奇异积分算子的加Lp有界性。 定义2:设函数K∈L2(Rn)满足条件: (1)‖K‖L∞≤C; (2)|K(x)|≤C|x|-n; (4)对于1 ander条件。张璞等在文献[8]中证明满足上述Lr-Hörmander条件的奇异积分算子是Lp有界的。 令b为Rn上的局部可积函数,其与T生成的交换子定义为: Tb(f)(x)=b(x)Tf(x)-T(bf)(x)。 本文主要结果如下。 首先,回顾一些基本定义。 定义3:令Φ={φ1,…,φl}为Rn上的有界函数,对局部可积函数f,定义Φ sharp极大函数为 φi(xQ-y)|dy, 其中下确界取遍所有的1重复数{c1,…,cl},xQ为方体Q的中心。 本文中,Q表示Rn中的方体,给定方体Q和Rn上的局部可积函数f,令 和 众所周知(见文献[3,7]), 如果M#(f)(x)属于L∞(Rn),则称函数f属于BMO(Rn),且令 ‖f‖BMO=‖M#(f)‖L∞。 根据文献[7],有 ‖f-f2kQ‖BMO≤Ck‖f‖BMO。 记 下面引入一些证明过程中需要的引理。 引理1[8]:令T为定义1所述奇异积分算子,则T在Lp(Rn)(1 f(y)dy。 固定方体Q=Q(x0,d),使得x∈Q,则 Tb(f)(x)=(b-bQ)Tf(x)-T((b-bQ)f) (x) 因此 下面分别估计Ⅰ与Ⅱ。首先估计Ⅰ。利用Hörmander不等式, 为估计Ⅱ,将f分解:f=f1+f2,其中f1=fχ2Q(x),f2=f-f1。则 再分别估计Ⅱ1和Ⅱ2。选取1 对Ⅱ2,当x∈Q时,有 针对Ⅱ21,利用|b2k+1Q-b2Q|≤k‖b‖BMO, 根据Hölder不等式,有 对Ⅱ22,取t>r,使用Hölder不等式,有 综上所述,得 最后证明定理2。 定理2的证明:在定理1中,选取1 [1] Coifman R R,Rochberg R,Weiss G.Fractorization theorems for Hardy spaces in several variables[J].Ann.of Math,1976,103:611-635. [2]Janson S.Mean oscillation and commutators of singular integral operators[J].Ask.Math,1978,16:263-270. [3]Trujillo-Gonzalez R.Weighted norm inequalities for sing- ular integral operators satisfying a variant ofHörmander′scondition[J].Comment.Math.Univ.Carolin,2003,44:137-152. [4]Pe′rezC.Endpoint estimate for commutators of singular integral operators[J].J.Func. Anal,1995,128:163-185. [5]Garcia-Cuerva J,Rubio de Francia J L.Weighted Norm Inequalities and Related Topics[J].North-Holland Math.Amsterdam,16,1985. [6]Grubb D J,Moore C N.A Variant ofHörmander′s condition for singular integrals[J].Colloq.Math,1997,73:165-172. [7]Lorente M,Riveros M S,de la Torre A.Weighted estimates for integral operators satisfyingHörmander′s condition of Young type[J].Journ Fourier Anal Appl,2005,(11):495-509. [8]张 璞,张代清.变形Hörmander条件与奇异积分算子的加权估计[J].数学学报,2013,56:223-233. TheLpBoundednessforCommutatorsofSingularIntegralOperatorsSatisfyingaVariantofHörmander′sCondition CAO Mei-yang (College of Mathmatics & Information Science,Jiangxi Normal University,Jiangxi Nanchang 332200 PRC) In this paper,we have proved the sharp maximal function inequalities for a class of commutators related to the singular integral operators satisfying a variant ofHörmander′s condition.As an application,we get the boundedness of the commutators on Lebesgue spaces. Commutators,Singular integral operators,Sharp maximal function 2013-12-20; 2014-01-21 曹美阳(1990-),女,江西九江人,在读硕士研究生,专业方向基础数学调和分析。 国家自然科学基金项目(11261023);江西省自然科学基金项目(20122BAB201011)。 1001-3679(2014)01-0008-04 O1742 A
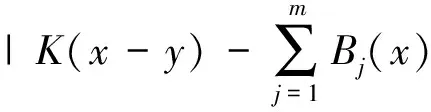
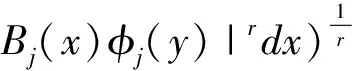
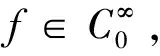
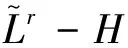
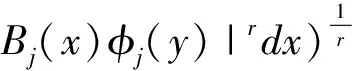


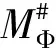

2 预备知识和需要的引理



3 定理的证明