基于波束成形理论的传声器阵列声场仿真分析
刘洛斌, 李舜酩, 丁 一, 韩佳欣
(南京航空航天大学 能源与动力学院,江苏 南京 210016)
基于波束成形理论的传声器阵列声场仿真分析
刘洛斌, 李舜酩, 丁 一, 韩佳欣
(南京航空航天大学 能源与动力学院,江苏 南京 210016)
基于用传声器阵列测量空间声场信息的波束成形技术,在声场可视化和噪声源识别中得到了广泛的研究与应用。利用波束成形技术分析噪声源时,不同的传声器阵列布局会对分析结果产生不同影响。在合理化假设的条件下,基于MATLAB软件对线性、矩形、圆形、半圆形4种不同阵列的处理效果进行仿真,并对仿真结果进行分析。比较识别精度、传声器数目和图形对称性等综合因素,得出圆形阵列具有最好综合效果的结论。
波束成形;传声器;阵列;声场;仿真
波束成形技术(又名麦克风阵列)是一种基于传声器阵列测量的空间滤波技术。在传声器阵列信号处理发展中,波束成形技术一直是阵列信号处理的核心。1974年Billingsley[1]把该技术运用到声学领域中,波束成形从此作为一种噪声源识别方法。随着近几年数据采集技术和计算机处理技术的发展,该技术可以完成声场的可视化测量,被广泛应用于声源识别定位中[2]。波束成形的基础是传声器阵列的指向性原理,而传声器阵列性能的高低决定了波束成形方法识别声源的能力大小,因此传声器阵列的研究对波束成形的进一步发展具有极其重要的意义。如何选出旁瓣级别最小、主瓣较窄并具有较好实用性的阵列,一直是国内外学者的研究热点,这也对实际测量中阵列的设计选型具有指导意义。
1 基本原理
1.1波束成形技术
1.1.1波束成形原理简介
作为一种阵列信号处理技术,波束成形方法的基础是传声器阵列测量。具体到声源识别中的波束成形方法是根据声程差的不同而产生的相位差,来确定信号的来源方向,其中声程差来源于传感器接收声波时间的差异与传感器本身的位置。对于传声器阵列而言,当各阵元接收的信号都是同向时,阵列可以产生一个增强的信号输出,否则输出将被减弱。波束成形的目的就是选取适当的加权向量,对传声器阵列中各阵元的输出进行延时、加权、求和等运算,以补偿各阵元上的传播延时,从而使某一期望方向上的信号到达阵列后都是同向的,进而在该方向上产生一个空间响应极大值,达到空间滤波的目的,以实现定向作用。因此,波束成形技术还可以实现声源定位,实现声场的可视化测量。其原理是:对传声器阵列测得的振速或声压数据进行处理(时域延时求和、相移频域算法或波束形成去自谱算法等),在重建声源表面上得出声源分布图,完成声场可视化测量,直观定位声源位置。
1.1.2波束成形技术的特点
波束成形技术的特点是,不但能够得到需要分析的整个物体表面的声场辐射特性,而且能够对声源进行频域上的分析,从而进一步得到声源所包含的主要频率成分在声源上的分布情况。与传统的单个定向传声器相比,处理阵列信号时,传声器阵列是按一定方式布置在不同空间位置上的,利用了信号的空域特性来增强信号及有效提取信号的空域信息,因此波束成形技术具有灵活的波束抑制、较高的信号增益、较强的抗干扰能力以及较高的空间超分辨能力等优点,受到广泛关注。
目前,波束成形技术已经广泛应用于雷达、通信、电子对抗、声呐等军事技术领域以及航空航天技术、工业无损测试技术、汽车工业技术和材料研究等领域,并且在这些领域都取得了良好的应用效果。
1.2阵列指向性
波束成形技术基于传声器阵列的指向性原理,下面利用空间离散分布的多基元基阵对该原理进行阐述。如图1所示,设有空间任意分布的N个无指向性传感器,图中Hi表示第i个传感器,其直角坐标为(xi,yi,zi),球坐标为(θi,φi,γi)。

图1 指向性原理示意图
分析阵列指向性时,计算各传感器之间的声程差是关键,基于以上坐标假设有:
(1)
从而求得信号入射方向(θ,φ)与OHi夹角δi的余弦:
(2)
以坐标O为参考,从图1中可得Hi到参考点的声程差为:
di=ricosδi=xisinθicosφ+yisinθsinφ+zicosθ
(3)
得相位表达式:
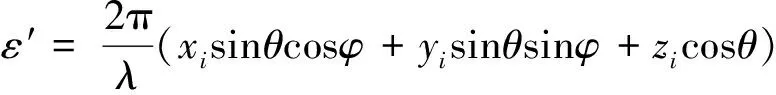
(4)
当基阵指向(θ0,φ0)时,Hi信号补偿相位为:
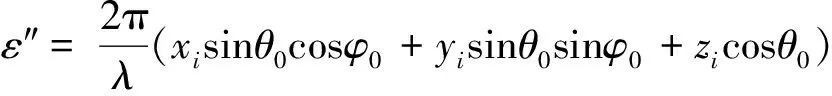
(5)
即Hi信号经移相后为:
式中:Δεi=ε′-ε″。
对N个基元求和后得:
(6)
由指向性函数的定义得指向性函数为:
(7)
指数形式下:
(8)

阵列的指向性函数表示阵列对各个方向信号的接收或者抑制能力,不同阵列的指向性函数略有不同,但均可通过以上基本原理推导,在此仅列出线阵的指向性函数式与平面阵的指向性函数式式(7),推导过程省略。
线阵的指向性函数式:
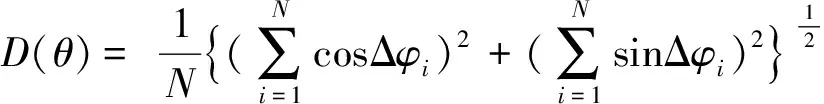
(9)
而对于圆柱阵、圆周阵等特殊阵列,应选取能简化指向性函数的参考点进行计算,限于篇幅,此处不一一赘述。
2 传声器阵列的布局设置及其几何参数
这里采用若干个传声器在指定空间的固定范围内(1m×1m的方形区域)组成一块传声器阵列区域,对空间声场进行测量,由此通过传声器阵列的布置对空间辐射声场的声学信号进行收集和后期特殊的处理,从而提取出收集的信号里所包含的能反映出空间辐射声场状态的特征参数。与此同时,过滤或抑制掉其他干扰噪声信号以及不影响实验分析的声学信号,这样就可以获得详细的有关声场的声源信息。
传声器阵列是由若干个传声器在指定空间按照一定规律排列组合而成的声信号测试、收集与处理设备。
理论上,阵元的间距、几何尺寸和数目对于指向性有着直接而明显的影响:随着阵元间距的增加,主瓣的宽度变窄,旁瓣增多,指向性增强;随着阵元尺寸的增大,主瓣的宽度变化不大,旁瓣的幅值减小;随着阵元数目的增加,主瓣变窄,旁瓣幅值减小[4]。
因此,首先假设现有参数设计如下:阵列布局的设置范围选取为1m×1m的方形空间区域,测量的噪声频率范围为500~5000Hz(波长为0.068m~0.680m)[5]。借鉴时域采样的原理,传声器阵列测量时一般采用λmin/2的间距,其中λmin是阵列测量的噪声源最短波长,因此取阵元布置的最小间距为λmin/2,这里约为0.034m。
根据MATLAB仿真,所选择的4种布局方式分别为线形阵列、矩形阵列、圆形阵列和半圆形阵列。
2.1线性阵列
根据选取的1m×1m的方形区域和阵元布置的最小间距λmin/2=0.034m,得到线性阵列的传声器数目为1/0.034≈29,线形阵列布局示意图如图2所示。

图2 线形阵列布局示意图
2.2矩形阵列
根据选取的1m×1m的方形区域和阵元布置的最小间距λmin/2=0.034m,得到矩形阵列的传声器数目为(1/0.034)2≈292=841,矩形阵列布局示意图如图3所示。

图3 矩形阵列布局示意图
2.3圆形阵列
根据选取的1m×1m的方形区域和阵元布置的最小间距λmin/2=0.034m,得到圆形阵列的传声器数目为(π×1)/0.034≈92,圆形阵列布局示意图如图4所示。
2.4半圆形阵列
根据选取的1m×1m的方形区域和阵元布置的最小间距λmin/2=0.034m,得到半圆形阵列的传声器数目为(π×1)/(2×0.034)≈46,半圆形阵列布局示意图如图5所示。

图4 圆形阵列布局示意图

图5 半圆形阵列布局示意图
3 软件仿真
本节在前面波束成形理论和阵列布置研究的基础上,运用MATLAB软件仿真模块比较4种传声器阵列布局对噪声源的识别效果。
这里采用控制变量的方法,在选取的面积大小相同的区域内按照阵元间最小间距来布置传声器阵列,综合分析所需要的传声器数目和仿真结果图,比较得出4种不同传声器阵列布局各自对噪声源识别效果的优劣。
3.1仿真条件假设
3.1.1各向同性介质假设
顾名思义,各向同性介质就是物理性质与方向无关的地球物理介质,介质的弹性参数与波的传播方向无关,这也是一种理想化模型。这里为方便研究,假设声信号传播的介质是各向同性介质。
3.1.2球面波假设
在实际生产中,各种各样噪声源的形状难以简单描述出来,想要完全精确地描述出声源状态及其声音场信息难度很大。这里参照物理学上提出的理想模型的方法,在不严重影响所研究问题结果的前提下提出球面波的假设:球面波的波线是自球心引出的一簇射线,其球心是以点声源的形式存在。一个在真空或各向同性介质中的理想点声源,它向外发射的声波是球面声波,等相位面是以点声源为中心、随着距离的增大而逐渐扩展的同心球面。
3.1.3点声源假设
在空间上仅有明确位置而无范围的声源称为点声源。讨论声辐射时,定义点声源的概念是方便的,只要声源尺寸远小于其辐射的声波波长即可。
3.2仿真结果
通过MATLAB软件的仿真功能,由编入的程序得到了所需要阵列的水平方向和垂直方向上的二维指向性图,如图6,7所示。
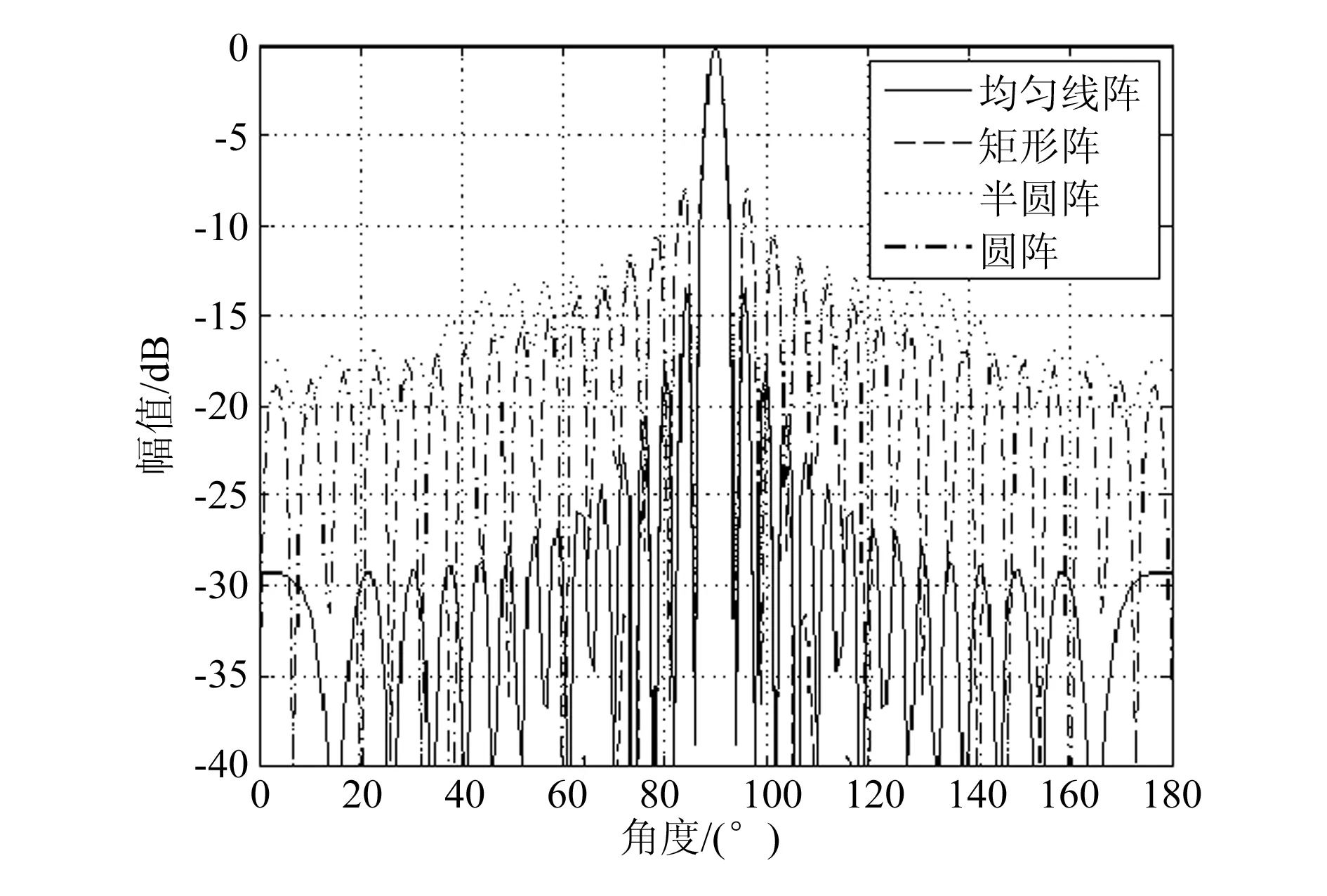
图6 水平方向二维指向性图

图7 垂直方向二维指向性图
3.3仿真结果分析
评价阵列优劣的主要指标是主瓣宽度和旁瓣数目及幅值。主瓣宽度越小,旁瓣越少、幅值越小,则这个阵列的测试性能和识别效果也越好。
由图6可见,水平方向上4种阵列的主瓣宽度相差不大,但是旁瓣的差别明显。
a.矩形阵列的旁瓣级数目最少,并且旁瓣级幅值最低,因此在相同面积的空间区域里不考虑所用传声器数目的前提下,矩形阵列的识别效果是最突出的。但是,在实际生产中不可能实现在局部范围里布置数量如此之多的传声器以达到预期的识别效果,需要根据识别精度和经济效益等多方面综合考虑,所以矩形阵列的选取还有待商榷。
b.半圆形阵列的旁瓣较多并且幅值较大,明显不如矩形阵列的识别效果,但是较之于矩形阵列有所需传声器数目更少的优势。
c.圆形阵列的旁瓣状况明显优于半圆形阵列,旁瓣更小,但这是以布置双倍的传声器数目为代价的。综合各方面效果,例如图形的对称性和方向角设置等,圆形阵列的识别效果还是要优于半圆形阵列。
d.从布置阵列所需的传声器数目上看,线性阵列所需传声器数目仅为圆形阵列的1/3;从二维指向性图上来看,线性阵列的旁瓣较少并且幅值明显小于圆形阵列和半圆形阵列,旁瓣状况显然优于圆形阵列和半圆形阵列。但是圆形阵列较之于线性阵列的这种劣势是有其理论上的必然性的,这正是由圆形阵列的非线性引起的,其原因有二:第一,杂波阶次的增加(类似于线性阵列中速度向量与阵列轴线没校准而引起的杂波阶次增加);第二,杂波轨迹随距离而发生变化,这是由于圆形阵列的引导矢量随距离发生变化而引起的[6]。
为克服圆形阵列的这一缺陷,也有专门的改善措施:通过引入有向阵元并选取适当的辐射函数,就可以有效地改善圆形阵列的方向图特性。
综上所述,尽管圆形阵列相比于矩形阵列有伴随着较差旁瓣状况的劣势,但是在布置阵列所需的传声器数目上有着极大的优势:其所需的传声器数目仅为矩形阵列的1/9,在识别精度允许范围内以及从经济成本角度考虑是可以弥补其在旁瓣状况上的劣势,况且这一劣势还可以通过设置有向阵元及辐射函数来弥补。
又考虑到圆形阵列的图形对称、能够提供全方位的方位角等特点,抛弃了半圆形阵列的选择。而线性阵列的布置过于简单,且从图形形状角度考虑,其空间分布不如圆形阵列好。
因此,在现有仿真条件设置下,圆形阵列最佳,其识别效果最好。
4 研究总结及展望
4.1研究总结
通过以上的分析,可以得出如下结论:
a.在通常的噪声识别方法中,仿真占有举足轻重的作用。通过MATLAB软件仿真可以很容易地得到特定波长条件下的指向性图像,并能从图上读出所需要的能够比较布局效果的信息。
b.测量阵列的传声器数目对仿真结果有很大影响。阵列布置的传声器数目越多,仿真效果越理想,对应的测量结果越精确。
c.在某些情况下软件仿真结果会与现有理论结果不一致,这是由仿真计算的边界或载荷条件的简化造成的。综合阵列布置的图形特点和圆形阵列的非线性及杂波阶次条件,就可以得到正确的结论:圆形阵列的识别效果优于线性阵列。
4.2研究展望
本次仿真研究的指向性图像只限于二维空间,构造三维空间的阵列布置函数,即可同样通过MATLAB仿真出更为直观的三维指向性图像。其效果将更明显地反映出同一阵列主瓣、旁瓣级之间的区别以及不同阵列的主瓣、旁瓣级之间的差异。进一步的研究可以集中于创造出更高级的图形布置(例如叠加、旋转、对称图形等)、开发出更新型的图形函数以及比较创造出的不同图形阵列的仿真效果。
[1] Billingsley J, Kinns R. The acoustic telescope [J]. Journal of Sound and Vibration,1976,48(4): 485-510.
[2] 褚志刚, 杨洋, 倪计民,等. 波束形成声源识别技术研究进展[J]. 声学技术, 2013, 32 (5): 430-435.
[3] 孙运强, 李在庭. 声阵列指向性函数计算[J]. 测试技术学报, 1996,10(2):719-724.
[4] 巩建辉,严碧歌. 基于不同阵元换能器阵列的指向性研究[J]. 西北师范大学学报:自然科学版,2011,47(3): 35-39.
[5] 赵芳芳. 波束形成方法在噪声源识别应用中的仿真和实验研究[D]. 上海: 上海交通大学, 2007.
[6] 赵雅靓,张连堂,刘先省. 圆形阵列与线性阵列方向图的比较与分析[J]. 河南大学学报:自然科学版,2005,35(2):72-75.
AcousticFieldSimulationAnalysisofMicrophoneArrayLayoutBasedontheTheoryofBeamForming
LIU Luobin, LI Shunming, DING Yi, HAN Jiaxin
(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)
Based on the beam forming technology, it utilizes the microphone array layout to attach information of the specific acoustic field, analyzes the visualization and identification of noise sources. It shows the various influences of different microphone array layout, demonstrates the process and analysis of different layout simulation with rational hypothesis among linear, rectangle, circle and semi-circle via Matlab. Considering the identification accuracy, the number of microphones required and graphic symmetry, the simulation result shows that the circle layout is highly effectivs.
Beam Forming; Microphone; Array Layout; Acoustic Field; Simulation
10.3969/j.issn.2095-509X.2014.05.019
2014-04-20
刘洛斌(1993—),男,江苏扬州人,南京航空航天大学本科生,专业为能源与动力学院飞行器动力工程。
TB52; TB559
A
2095-509X(2014)05-0071-05

