考虑负载变化的机床传动系统时变动特性研究

张会杰，刘海涛，张 俊，赵万华

(西安交通大学 机械制造系统工程国家重点实验室，西安 710054)

工件在加工过程中，由于材料去除率大(如航空薄壁件加工过程中，材料去除率能达到90%以上)，所以丝杠传动系统的驱动负载变化也较大，而负载的大变化进而会引起丝杠传动系统的动态特性变化，进一步决定了该进给轴的控制性能[1-2]，从而影响被加工件的加工质量[3-4]，所以有必要研究机床传动系统的固有频率和加速度振动响应随负载变化的变化规律。

针对丝杠传动系统的研究大都以集中参数法[5-6]、有限元法[7]或两者相结合的方法[8-9]及其它方法[10-11]。学者[5-11]虽然对传动系统建模及其动特性的研究有很大的贡献，但都是基于静态下的某个特定位置(如丝杠中间处)进行研究的，并没有考虑负载变化对传动系统动态性能的影响;而Brussel等[12]则将鲁棒算法和滑模控制应用于考虑直线电机驱动工作台的变质量系统中，但并没有考虑直驱负载变化下该直驱系统动特性的变化规律；而文献[13-15]采用有限元方法分析了质量空间分布变化下其系统动态性能的变化规律，但Zhou等[16]进一步理论分析了丝杠在自由状态下随不同负载的扭转振动特性变化规律。然而，实际上丝杠是被固定(两端固定或一定固定)在床身上，由电机通过联轴器驱动(或直驱)丝杠旋转，带动工作台往复运动，当负载变化较大时，其传动系统的动态特性会发生演变。因此，有必要建立考虑负载变化和导轨滑块副摩擦特性的机床传动系统等效动力学模型，并进行动特性研究。

本文采用集中参数法建立了考虑负载变化和导轨滑块副摩擦特性的传动系统等效动力学模型，理论分析了传动系统的等效阻尼系数，以及固有频率、加速度振动响应随负载变化的变化规律。最后以本实验室RTLX660数控机床Y轴滚珠丝杠驱动工作台传动系统为例，进行了实验验证。

1 滚珠丝杠传动系统动力学建模

1.1 丝杠传动系统物理模型的等效

丝杠传动系统的动态性能影响着被加工件的加工质量[1-2]，尤其传动方向的动态性能，因此有必要研究传动系统的动态特性。图1是典型数控机床传动系统结构及物理模型。主要由床身、工作台、滚珠丝杠副、导轨滑块副、电机、支撑轴承等主要部件构成。图2、3分别是轴承安装方式(成组布局)示意图及系统等效动力学模型。本文主要考虑丝杠杆拉压刚度、轴承副和丝杠螺母副的轴向接触刚度，则忽略了固定结合部传动方向的切向刚度及伺服刚度等非主导因素。

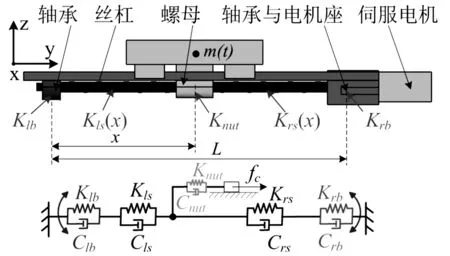
图1 传动系统结构及等效物理模型

图1、3中：m(t)为丝杠传动系统驱动负载的质量，fc为运动方向的摩擦力，x、L分别为丝杠螺母与左侧支撑轴承之间的距离、整个丝杠的长度，Kls、Krs、Cls、Crs分别为螺母两侧丝杠杆的广义轴向刚度与阻尼，Klb、Krb、Clb、Crb分别为左、右轴承的轴向接触刚度与阻尼，Knut、Cnut是丝杠螺母副轴向接触刚度与阻尼。

图2 轴承安装方式示意图

图3 传动系统等效动力学模型

根据图3中的等效动力学模型，建立了考虑负载变化和导轨滑块副摩擦特性的传动系统动力学方程，如下：

(1)

式(1)中：m-Δm(t)、c、ke分别为传动系统传动方向的负载(为被工件质量、工作台质量、夹具质量、螺母底座等的总质量，单位kg)、粘性阻尼系数(Ns/m)、等效刚度(N/m)，而负载在大切除的加工过程中随时间而变化；、分别为负载沿传动方向的位移(m)、速度(m/s)、加速度(m/s2)矢量，Fsinωt为交变切削力，fc(m-Δm(t))为摩擦力(N)，是负载的函数，有如下表达式：

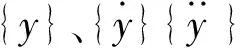
fc(m-Δm(t))=-μf×Q×Sgn(rtre)

(2)

式(2)中：m为初始负载，Δm(t)是负载的变化量，在机床加工过程中，负载变化量随时间而变化；Q为导轨滑块副内部所有滚子的压力之和，Sgn(rtre)为符号函数，与滚动体的滚动趋势有关，μf为干滚动摩擦系数，呈现为非线性变化，其中μf为

(3)

式(3)中：Qi为每个滚子的受力，E为弹性模量，μ为泊松比，R为滚子半径。式(3)是根据参考文献[17]进一步推导得出的。

1.2 等效阻尼系数确定

滚动导轨滑块副阻尼的机理较为复杂，既有库伦摩擦阻尼，又有粘性迟滞阻尼，还有滚动体之间相互碰撞的冲击阻尼(无保持架导轨滑块副)，当导轨滑块副润滑条件欠缺时或者处于干摩擦条件下，库伦摩擦阻尼占主要部分，而本文则主要考虑库伦摩擦阻尼。

等效阻尼系数的确定采用在一个振动周期内能量消耗相等的方法进行求得。假设该系统振动位移的稳态解为振幅为A的简谐振动，形式如下：

y=Asin(ωt-φ)

(4)

式(4)中：A为振动幅值(单位m)、ω为振动的圆频率(单位rad/s)、φ为初始相位，则系统振动速度稳态解为

(5)

设该系统的一个振动周期内，其运动结合部的库伦摩擦力消耗的能量为

(6)

(7)

令E1=E2，有下式：

4Afc(m-Δm(t))=πceωA2⟹

⟹ce=4fc(m-Δm(t))/(πωA)

(8)

此时，式(1)可以简化为：

(9)

1.3 理论分析

1.3.1 固有频率

对于单自由度系统而言，其传动方向的固有频率可根据下面公式进行求得：

(10)

式(10)中：π为圆周率常数，等效刚度ke是由丝杠螺母副、轴承副的轴向接触刚度与丝杠本身的拉压扭转刚度串、并联构成(Kls与Krs串联，Klb与Krb串联，上述两者并联再与Knut串联)，表达式如下：

(11)

从式(10)可以知：当传动方向的等效刚度一定时，传动方向的固有频率由负载大小所决定，因此，在工件大切除率的情况下，必须要考虑固有频率随负载变化的变化规律。其中，等效刚度ke中的相关参数由下面公式求得：

(12)

(13)

(14)

式(12～14)中：x、L分别为丝杠螺母与左侧支撑轴承之间的距离、整个丝杠的有效长度，d为丝杠的底径，E、G分别为材料的弹性模量、切变模量，p为丝杠导程；Kh为赫兹接触系数，M是丝杠预拉伸扭矩，TC是预拉伸扭矩系数，dST是丝杠预拉伸螺母的公称内径，α为轴承的接触角，N为轴承的个数，n为单个轴承的滚子个数；P为双螺母的预紧载荷，α滚球与滚道的接触角，φ为丝杠的螺旋升角，ic为单螺母的承载列数，i为单螺母的承载圈数，d0为丝杠的公称直径，db为滚珠的直径。

式(12)是根据螺母两侧丝杠的受力形式，即靠近电机一侧Krs(x)不仅受拉压作用，而又受扭转作用，但另一侧仅Kls(x)仅受拉压作用，借助于杆理论和做功相等的原则，推导出螺母两侧丝杠杆的刚度计算公式；而式(13-14)分别是对角接触球轴承、丝杠螺母副进行受力分析并利用赫兹接触理论进行理论推导得出的其轴向刚度表达式。

1.3.2 传动方向的加速度频响

本文采用状态空间法先求传动方向的位移振动响应，之后再对位移求两次导数便可得到进传动的加速度振动响应。由于被加工件是连续切削的，故可将该系统认为是一个状态连续时变系统，表达式如下：

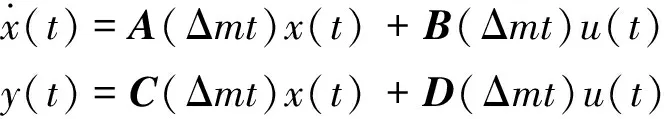
(15)

式(15)中：A(Δmt)为系统矩阵、B(Δmt)输入矩阵、C(Δmt)输出矩阵、D(Δmt)前馈矩阵(若系统没有直接从输入到输出的路径，此矩阵为零矩阵)，x(t)为状态矢量，y(t)为输出矢量，u(t)为控制矢量，其中系统矩阵A(Δmt)是式(9)中系数[M]、[C]、[K]的函数，表达式如下：

(16)

式(16)中：[M]、[C]均是负载的函数，随工件切除率不同而变化。

对式(15)进行拉普拉斯变换，进一步推导可得(推导过程中将A(Δmt)、B(Δmt)、C(Δmt)、D(Δmt)简化为A、B、C、D)：

(17)

对式(17)中的X(s)进行拉普拉斯反变换，可得：

(18)

式(18)中：第一项为初始状态下的响应，第二项为力函数作用下的响应。将上式对t求两次导数，可得：

(19)

将式(15)中的y(t)求两次导数(假设D(t)=0)，并将式(19)代入，可得传动系统的加速度振动响应：

(20)

式(20)中：A、B、C分别为A(Δmt)、B(Δmt)、C(Δmt)，当初始条件x(0)=0，上式可以简化为：

(21)

2 数值分析与实验验证

2.1 数值分析

以RTLX660数控机床Y轴滚珠丝杠传动工作台系统为例，当工作台以静止状态处于丝杠中间时，理论分析了该传动系统动特性随负载变化的变化规律，并进行了实验验证。

以中长期债权或股权为主要投资工具，政府引导基金在推动新兴产业成长方面发挥着重要的作用。相对于银行、共同基金等金融机构，政府引导基金在项目选择上具有更强的倾向性，通过特定的投资准则对具体的产业或项目提供金融支持，成为新兴产业成长发展的重要融资渠道。我国最早的政府引导基金产生于2002年，其提供的发展资金成为北京中关村迅速成长的重要因素。截至2017年7月底，国内共成立1660支政府引导基金，资产总规模达到约8万亿元，成为政府引导产业发展的重要工具。

将该机床的数据代入相关公式进行计算，得到动力学方程(9)中的质量、阻尼与刚度系数。对该方程进行特征根求解，便可得到传动系统的固有频率的变化规律，如图4所示；图5则是等效阻尼系数随不同负载的变化规律；根据等效阻尼系数，采用状态空间法求解传动方向的加速度振动响应的变化规律，如图8(a)中的“仿真值(m=216 kg)”、“仿真值(m=256 kg)”、“仿真值(m=296 kg)”所示。

图4 固有频率随负载不同的变化规律

图5 等效阻尼系数随负载不同的变化规律

2.2 实验验证

本文利用LMS Test.Lab振动噪声测试与分析软件中的结构分析模态测试模块，采用Impact锤击法对RTLX660数控机床Y轴滚珠丝杠传动工作台系统进行测试，测试示意图如图6所示。

本实验将约为40 kg重的虎钳固定在工作台中间，在虎钳上夹持约为40 kg重的铁块(虎钳和铁块均视作负载)，并忽略上述固定结合部影响。在工作台的上表面对角处粘贴上三向加速度传感器，用来拾取在“敲击点”处施加沿正Y方向脉冲信号之后的工作台加速度振动响应信号，被测数据通过傅里叶变换处理之后得到的结果，将用来验证所建立动力学模型的准确性。图7是不同负载下工作台传动方向的加速度振动响应的测试结果。

图6 滚珠丝杠传动系统测试图

3 分析与讨论

3.1 负载变化对固有频率的影响

图4工作台固定在x/L=0.5处时其传动系统固有频率的变化规律，从图中可知：负载的变化量由0 kg变为60 kg时，其固有频率变化了11～12 Hz左右(变化幅度为12%左右)。因为该固有频率由传动方向的传动刚度和质量共同所决定，因此，当传动刚度一定时，负载变化对传动系统的固有频率起决定作用。

在切削过程中，材料的去除率是连续变化的，但为验证理论分析的正确性，只需针对几个特定的质量进行验证即可，因此，本文根据实际情况选择了三种负载质量，如：296 kg、256 kg、216 kg，进行了实验验证。表1则列出了进给系统工作台在x/L=0.5时，不同负载下传动系统固有频率的数值分析值与实验值。

从表1可知：当负载为216 kg时，固有频率的分析值与实验值的误差范围为11～12%；当负载为256 kg时，固有频率的分析值与实验值的误差范围为7～8%；当负载为296 kg时，固有频率的分析值与实验值的误差范围为6～7%。上述产生误差的原因是计算传动方向等效刚度时，忽略了轴承支撑座、电机座和螺母座固定结合部传动方向的切向刚度及伺服刚度等非主导因素，而负载为296 kg时的误差之所以比负载为216 kg时的误差小，是因为该误差不仅与上述等效刚度计算有关，还与对负载的灵敏度有关。

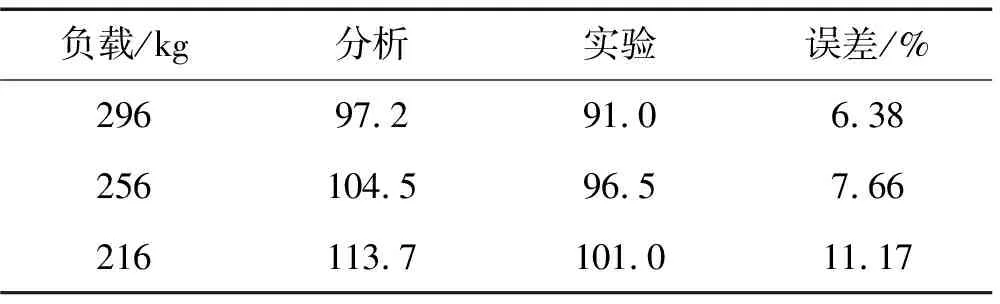
表1 频率随工件质量变化的演变规律(Hz)

3.2 负载变化对加速度振动响应的影响

通过模态分析和讨论得到传动方向的振动特性不仅与传动系统的传动刚度有关，还与传动系统的质量有关。由式(8)可知：等效阻尼系数与传动系统的驱动负载大小有关。

图8是不同负载下传动方向的加速度振动响应。图8(b)的实验值是对图7中不同负载下的实测数据，采用模态分解法进行分析而得到的。表2则列出了对应频率处的最大响应幅值。

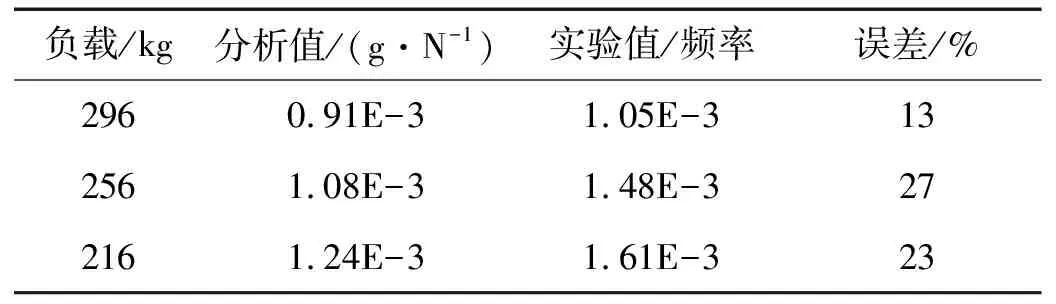
表2 加速度响应幅值随工件质量变化的演变规律(Hz)

从图8可知：实验分析验证了数值分析的正确性，即传动方向的加速度振动响应随负载不同会发生偏移，且数值分析值与实验值具有相同的趋势。

由表2可知：有的加速度振动幅值误差较大，主要是传动方向的阻尼系数存在不确定性或者随机性。

图7 不同负载下工作台的加速度振动响应

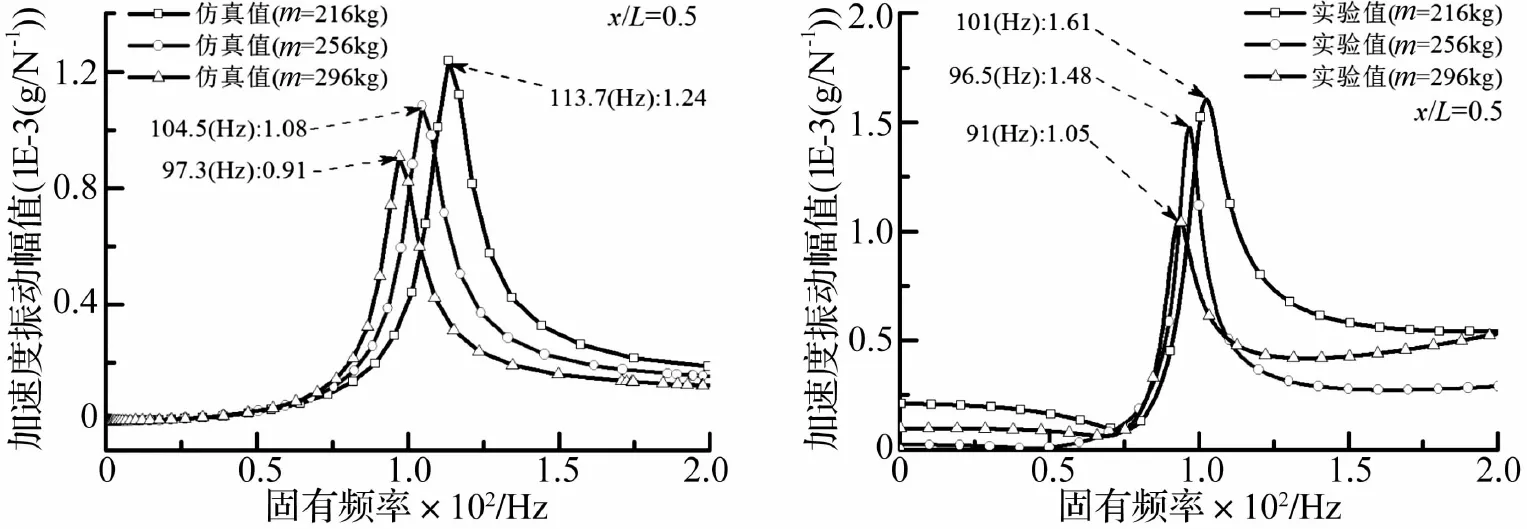
图8 不同负载下传动方向的加速度振动响应

从图8也可知：当系统负载变化时，传动方向的固有频率会逐渐偏移，当该频率在加工过程中被激起，传动方向将会有比较大的加速度振动幅值，将导致刀具受损、或颤振、或失稳，进一步降低加工质量。

综上所述，负载变化影响着传动系统的动态性能，尤其是在负载变化较大时(即被加工件处于大切除率时)，该动态特性的变化(称为“时变特性”)就不能忽略。该动态特性的变化规律能为机床切削加工参数提供理论依据。

4 结 论

本文建立了考虑负载变化的传动系统动力学集中参数模型，进行了动态特性的理论研究，并进行了相应的实验验证。理论分析和实验分析都表明负载变化影响着传动系统的动态性能，即传动系统在被加工件处于大切除率时存在时变特性。

(1)传动系统的等效阻尼系数随不同负载呈现出非线性变化，当负载的变化量由0kg变为80kg时，等效阻尼系数变化了18%左右；

(2)传动系统的固有频率随不同负载也呈现出非线性变化，当负载的变化量由0kg变为60kg时，固有频率变化了12%左右；

(3)传动系统的加速度振动响应也随负载不同而发生演变，当负载的变化量由0kg变为40kg 、80kg时，固有频率处的加速度振动幅值分别变化了19%、36%。

[1]Weck M，Krueger P，Brecher C.Limits for controller settings with electric linear direct drives[J].International Journal of Machine Tools and Manufacture，2001，41(1): 65-88.

[2]Weck M，In hand book of machine tool[M].New York: Wiley，1984.

[3]Kamalzadeh A，Erkorkmaz K.Accurate tracking controller design for high-speed drives[J].International Journal of Machine Tools and Manufacture，2007，47(9): 1393-1400.

[4]Kim M S，Chung S C.A systematic approach to design high-performance feed drive systems[J].International Journal of Machine Tools and Manufacture，2005，45(12): 1421-1435.

[5]邱国富.数控机床进给系统的研究[D].沈阳：东北大学，2006.

[6]王培功.XK717数控铣床进给传动系统的动力学建模及动态优化设计[D].杭州:浙江工业大学，2005.

[7]Zaeh M F，Oertli Th，Milberg J.Finite element modelling of ball screw feed drive systems[J].CIRP Annals-Manufacturing Technology.2004，53(1): 289 294.

[8]Okwudire C E，Altintas Y.Hybrid modeling of ball screw drives with coupled axial，torsional and lateral dynamics[J].Transactions of ASME，Journal of Mechanical Design，2009，131(1):1-9.

[9]Pislaru C.Hybrid modelling and simulation of a computer numerical control machine tool feed drive[J].Proceedings of the Institution of Mechanical Engineers.Part A，Journal of power and energy，2004,218(2):111-120.

[10]张涛，路长厚，李泉.基于扭矩测量的交流伺服工作台摩擦建模与仿真研究[J].润滑与密封，2006(4):32-35.

ZHANG Tao，LU Chang-hou，LI Quan.Study on friction modeling and simulation for AC servo worktable based on torsion measuring.Lubrication Engineering，2006(4):32-35.

[11]吴沁，芮执元，杨建军.考虑非线性弹性力的滚珠丝杠系统分岔与混沌特性分析[J].西安交通大学学报，2012(1):70-75.

WU Qin，RUI Zhi-yuan，YANG Jian-jun.Bifurcation and chaos characteristics for ball-screw system considering nonlinear elastic force[J].Journal of Xi’an Jiaotong University，2012(01):70-75.

[12]Van Brussel H，Van den Braembussche P.Robust control of feed drives with linear motors[J].CIRP Annals-Manufacturing Technology.1998，47(1):325-328.

[13]刘海涛，赵万华.基于广义加工空间概念的机床动态特性分析[J].机械工程学报，2010，46(21)：54-60.

LIU Hai-tao，ZHAO Wan-hua.Dynamic characteristic analysis for machine tools based on concept of generalized manufacturing space[J].Journal of Mechanical Engineering，2010，46(21)：54-60.

[14]Sriyotha P.A study on the dynamics and control of a CMM for high-speed operations [D].USA，University of California，Davis，2005.

[15]Van brussel H，Sas P，Istvan N，et al.Towards a mechatronic compiler[J].ASME Transactions on Mechatronics，2001，6(1):90-105.

[16]Zhou Y，Peng F Y，Chen J H，Torsion vibration analysis of lead-screw feed drives with changeable table position and work-piece mass[J].IEEE international Conference on Mechatronics and Automation，2007: 2194-2199，Harbin.

[17]吴二军，郭彤，李爱群.滚轴滚动摩擦系数研究与建筑物迁移工程水平动力计算[J].土木工程学报，2006，39(6):57-60.

WU Er-jun，GUO Tong，LI Ai-qun.A study on the rolling friction coefficient and the horizontal driving-force calculation in building monolithic moving engineering[J].China Civil Engineering Journal，2006，39(6):57-60.