基于多岛遗传算法的火箭炮初始扰动综合优化分析

冯 勇，徐振钦

(南京工程学院 机械工程学院，南京 211167)

火箭的发射精度受两部分因素影响：初始扰动与飞行扰动，火箭弹从定向器上完全脱离时的弹道偏差称为初始扰动。实践和理论分析表明，初始扰动主要由系统振动特性所决定，是影响火箭弹精度的主要根源。而火箭炮在连续发射过程中，前一枚火箭弹发射所引起的振动衰减到一定程度时，次一发火箭弹的燃气冲击力又作用到系统上，形成新的振动叠加。由于每一发火箭弹的燃气流冲击力大小不等，作用位置不断变化，外加系统各连接部位的连接刚度、阻尼的不同，使得火箭炮的振动变得相当复杂。由此可见，发射过程中发射间隔、相应的支撑刚度、阻尼的匹配等对火箭炮系统的初始扰动具有较大影响。

目前，对减小火箭炮初始扰动开展理论及仿真研究并不多见，芮筱亭等[1]通过优化射击顺序和射击时间间隔，提出了提高多管火箭射击密集度新技术；陈兵等[2]应用BP网络和自适应遗传算法开展了某型火箭炮变发射间隔对初始扰动的影响分析。上述研究均为单一因素分析，并未考虑与变发射间隔相匹配的变支撑刚度、阻尼的影响。本文在某型火箭炮发射动力学模型的基础上，采用多岛遗传算法，开展了变发射间隔及其与之相匹配的变刚度、阻尼优化分析，解决了单纯用动力学仿真或计算不能解决的问题，为提高发射精度、工程研制提供了理论支持。

1 弹-架系统的初始扰动计算

发射过程中，火箭弹在定向器上的运动姿态会受到多种因素影响而产生扰动。火箭弹从定向器上滑离瞬间，弹的纵轴及质心的速度矢量不沿定向器轴向线所确定的理论射向，此时弹所具有的角速度就称之为初始扰动，主要包括方向和高低两方面,是引起偏差与散布的主要原因。设弹体前定心部和后定心部中心间的距离为lB、质心到后定心部的距离为lR、弹体赤道回转半径为RA、Vf为中定心部离轨速度、V0为后定心部离轨的速度，则火箭弹在铅垂面内的初始扰动为[3]

(1)

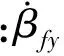
(2)

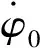
2 仿真模型的建立

2.1 仿真模型建立

多管火箭炮结构较为复杂，其结构如图1所示，经合理简化后建立其多体动力学模型，模型主要包含: 车体( 包括车大梁、板簧、铰接件)、轮胎、底座、回转支承、发射箱、定向器和火箭弹等构件。

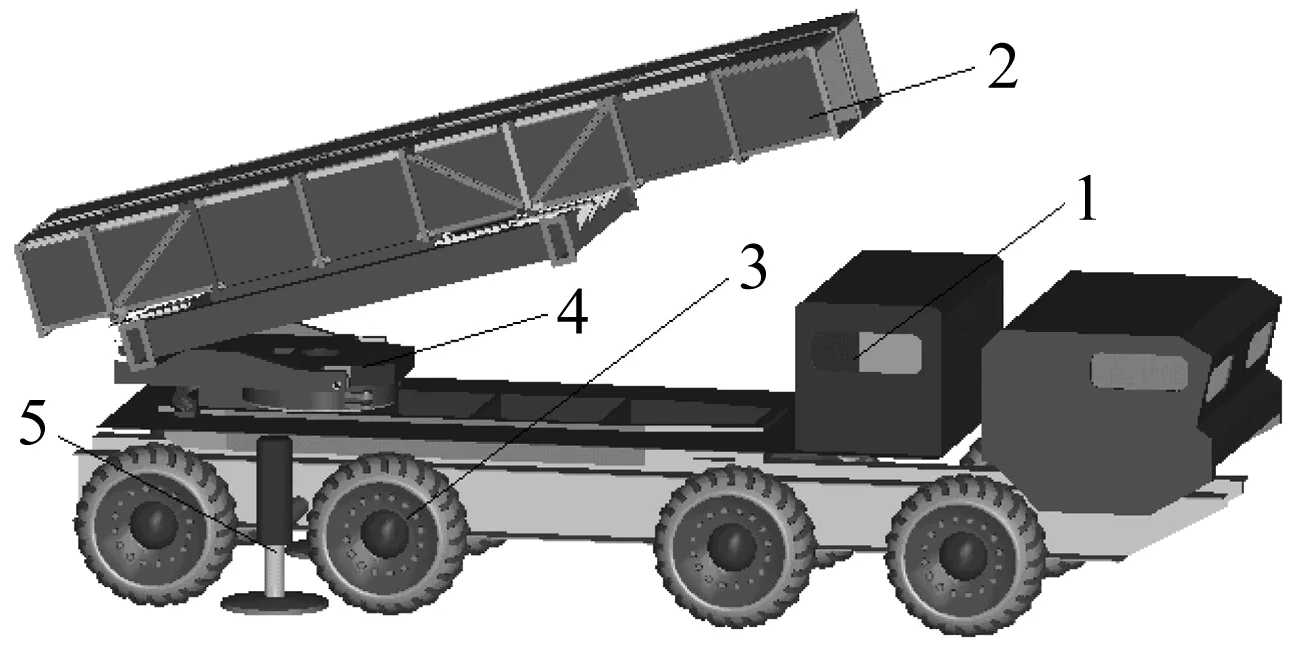
1.车体 2.发射箱 3.轮胎 4.回转台 5.支撑

对任意多体系统的拓扑构型表达方式而言，每个体记为Bi(i=1,……,N),N为系统中体的个数，铰用一条连接邻接刚体的有向线段表示，记为Hj(j=1,2,3……)，B0表示系统外运动为已知的刚体。本文所研究火箭系统的拓扑结构如图2所示，其中：发射管的柔性效应直接影响火箭弹出管的运动参数变化，将对初始扰动产生不可忽略的影响，因此模型中将与体B19～B26相联系的定向管建为柔性体；支撑B9、B10与地面B0间的铰h9、h10及回转台B16与起落架B17间的铰h24的功能主要通过液压系统得以实现，因此应建立机械系统与液压系统的耦合模型；车轮B1～B8与地面B0间的铰h1h8体现为轮胎与地面的弹性接触效应，因此在模型中应建立真实反映这种弹性效应的轮胎-地面接触模型[4-6]。

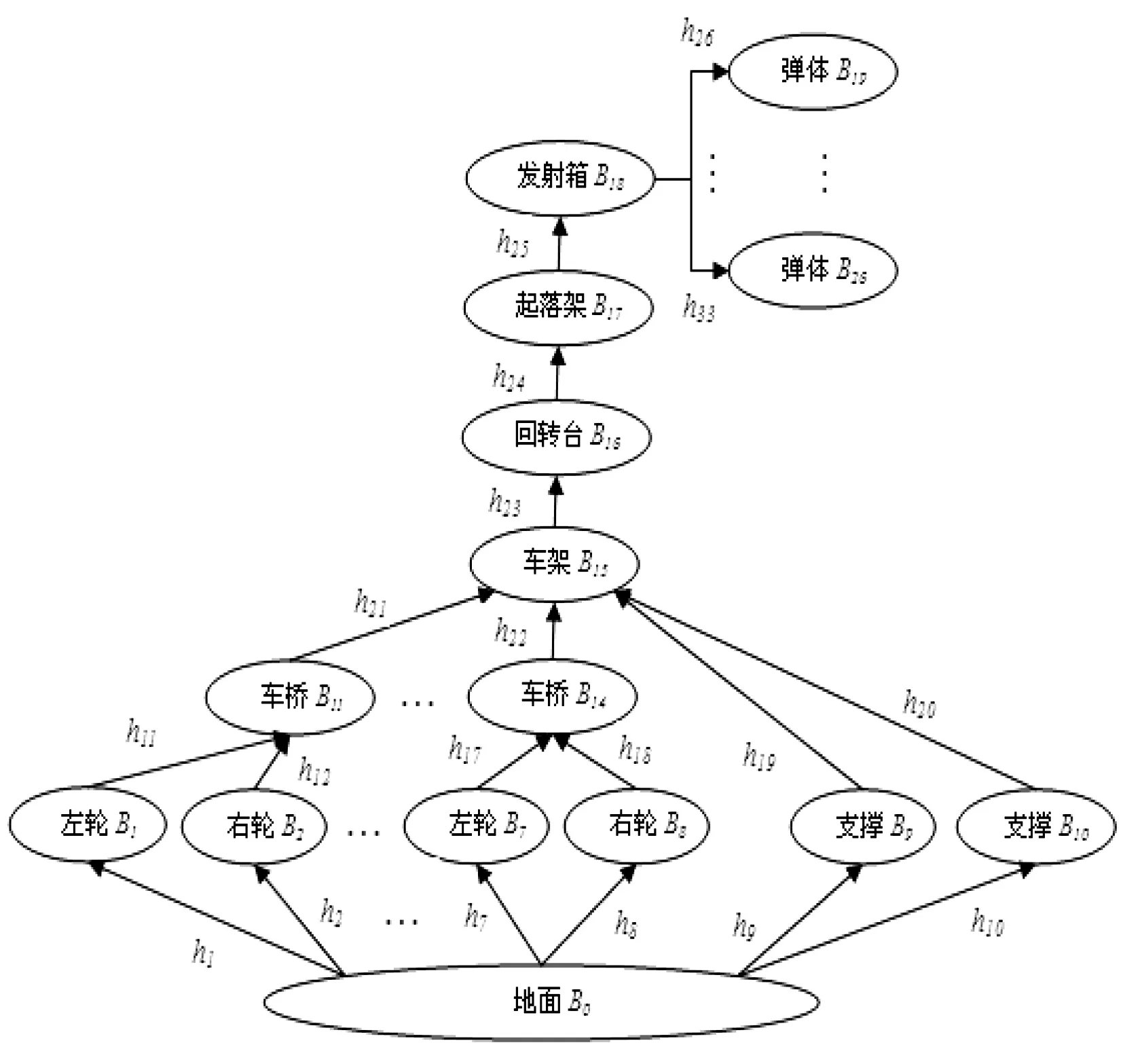
图2 某型火箭系统的拓扑结构

2.2 仿真模型验证

对仿真模型进行发射动力学仿真(高低射角16°；方向射角0°；发射间隔5s)，计算参考坐标系为：以回转台的中心为原点，车体前进方向为x方向；垂直于x方向并向上的方向为y方向；z方向由右手法则确定。

图3所示为三连发发射过程中发射架在高低平面内的角速度仿真变化曲线与定型样炮的角速度测试变化曲线对比图，由结果对比来看，仿真变化曲线与测试变化曲线基本吻合。由此可见，本文所建立的仿真模型及所确定的仿真参数是正确的，仿真所得到的结果是可信并可参考的。

图3 发射架在高低平面内的角速度仿真结果与测试结果对比

3 优化建模及分析

3.1 优化问题描述

对于火箭武器而言，单纯增加发射间隔将有利于提高火箭的发射精度，但不利于保持火箭武器火力的突然猛烈性，因此，在保持总的发射时间(40 s)不变情况下，要合理的分配发射时间间隔。与此同时，还要尽可能地减小火箭炮残余振动所产生的扰动，其直接有效的方法就是在火箭炮上安装必要的减振设施，使得在每一个发射间隔内都有一个最佳的连接刚度、阻尼匹配。就火箭炮系统来讲，起落部分与回转部分间以及回转部分与车体间的连接刚度、阻尼系数较小且直接影响火箭炮振动特性。综上所述，建立某型火箭炮减小初始扰动优化问题的数学模型为

(3)

式中：Eφ10( )及Eφ20( )为目标函数；TKi,TCi,SKi,SCi,Tj为优化变量，分别表示为回转部分的刚度系数、回转部分的阻尼系数、起落部分的刚度系数、起落部分的阻尼系数和每一枚弹的发射时间；k1、k2、k3、k4、c1、c2、c3、c4为约束界限值。

3.2 优化问题的实现

用传统方式对该优化问题进行求解，就必须对不同变量组合下的火箭炮模型进行发射动力学仿真，然后在每次仿真求得的结果中提取信息代入到目标函数中，通过目标函数的对比来最终得到最优解。这种方法的工作量极大，且无法得到全局范围内的优值组合。本文采用多岛遗传算法，借助动力学分析软件Adams所具有的强二次开发能力，编制仿真运行的控制程序，建立优化算法与动力学仿真的耦合。在本优化问题中共设定5个岛屿，每个岛屿有8个种子，进行10代遗传，整个优化过程共需要进行400次迭代[7-8]。

3.3 优化结果分析

应用上述方法对优化问题进行了优化求解，得到发射时间间隔的优化分析结果，结果如图4所示，由计算结果可以得出从第一枚弹在零时刻发射之后的每一枚弹的最佳发射时间分别为：3.439 9，9.085 0，14.340 0，20.457 4，25.691 5，31.922 0，34.981 3(单位：s)。

图5～图8分别为起落部分的最佳联接刚度、起落部分的最佳联接阻尼、回转部分的最佳联接刚度和回转部分的最佳联接阻尼变化图。由图分析可见，起落部分在不同发射时刻的最佳联接刚度为：10.915，14.768，8.008，13.066，14.371，7.225，7.912，13.117(单位：kN /mm)；起落部分在不同发射时刻的最佳联接阻尼分别为：671.833，245.675，489.769，93.988，688.322，995.402，326.492，798.173(单位：N.s /mm)。回转部分在不同发射时刻的最佳联接刚度为：4.16E10，6.87E10，5.85E10，7.55E10，9.05E10，9.19E10，8.85E10，4.16E10(单位：N.mm /rad)；回转部分在不同发射时刻的最佳联接阻尼为：1.46E9，6.74E8，8.63E8，9.26E8，2.54E9，4.87E9，2.92E9，1.08E9(单位：N·mm·s /rad)。

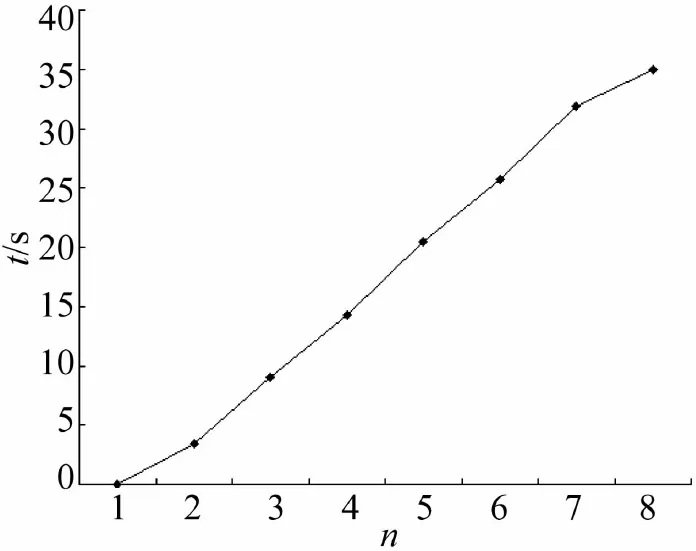
图4 最优发射时间曲线

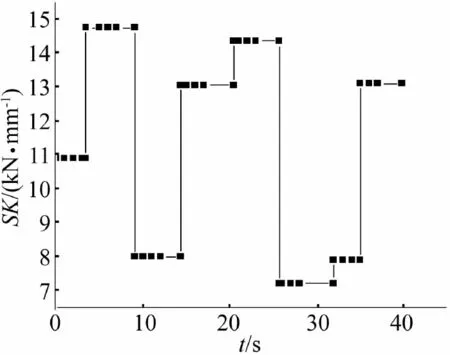
图5 起落部分最佳联接刚度时间曲线

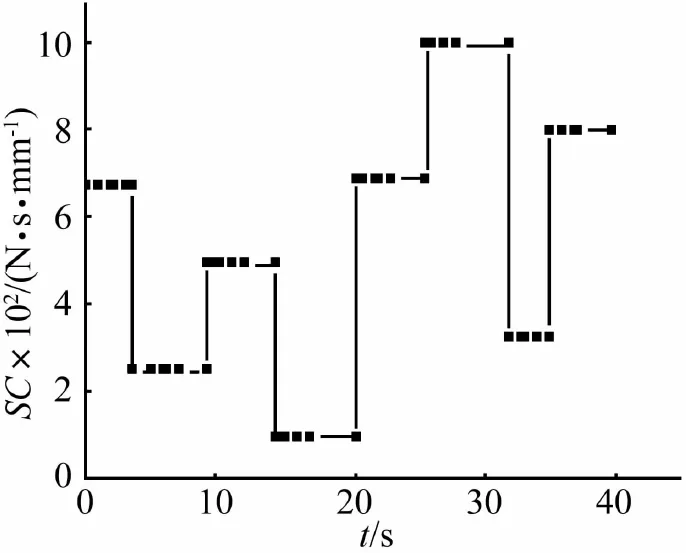
图6 起落部分最佳联接阻尼时间曲线

优化前与优化后火箭炮系统的初始扰动及其中间偏差的对比情况如表1所示，由对比结果可见，火箭炮系统的初始扰动量明显降低，表明本文优化所得到的参数是可行的，可以为相关火箭炮系统的研制和改造提供理论参考。

3.4 优化后系统仿真分析

采用以上优化分析所得到的最优参数对火箭炮系统进行了动力学仿真分析(高低射角16°；方向射角0°)，分析中将优化所得到的最优起落部分的刚度、阻尼变化和最优回转部分的刚度、阻尼系数分别以akispl函数的形式添加到仿真模型的弹簧阻尼器中。

图8、图9所示为火箭弹发射过程中发射架在高低平面和回转平面内的角速度变化曲线。由变化曲线可知，发射过程中发射架在回转平面内的最大角速度约为0.028 rad/s，出现在第五枚火箭弹飞出定向管的瞬间；而在高低平面内的最大角速度约为0.065 rad/s，出现在第四枚火箭弹飞出定向管的瞬间。

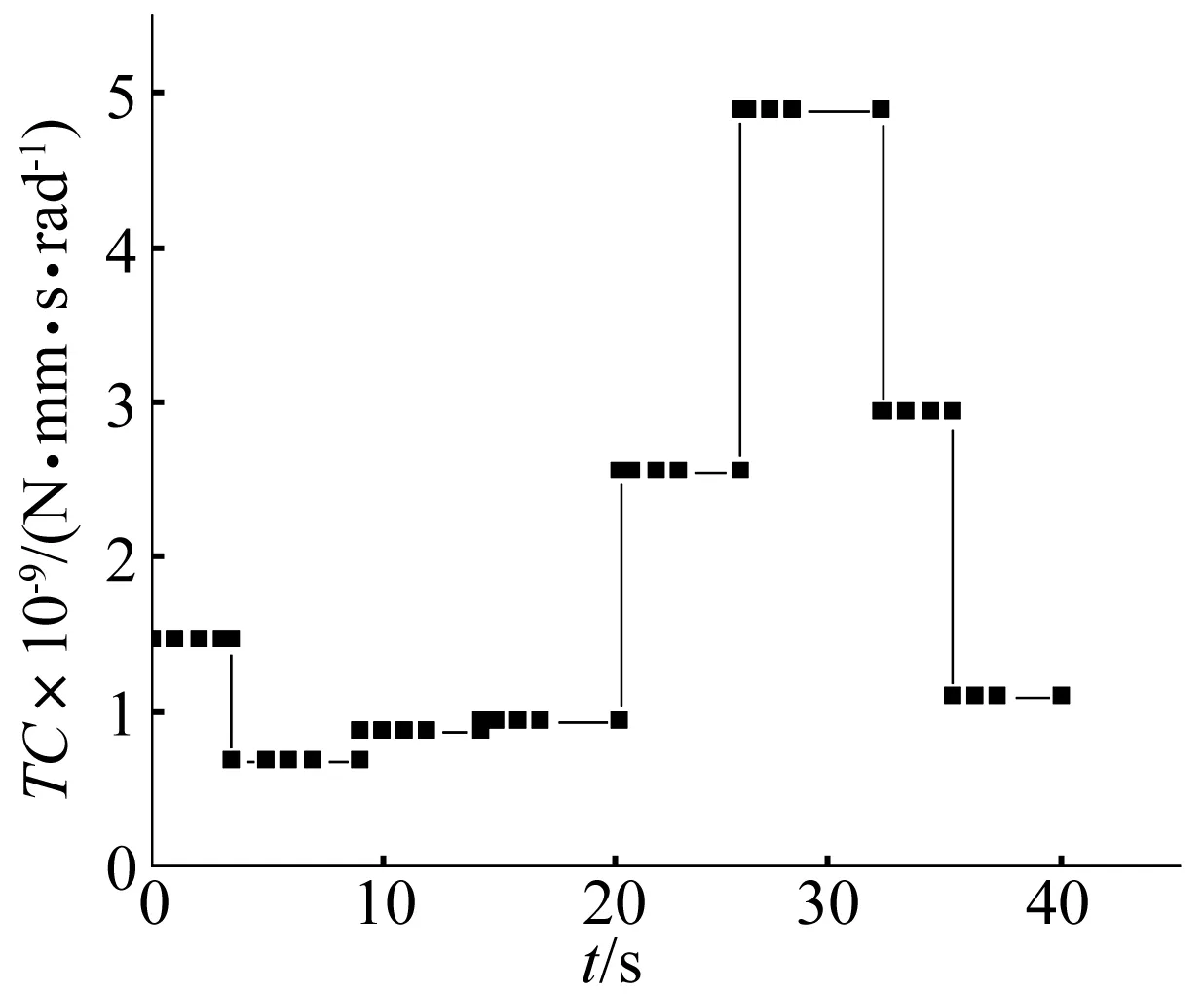
图8 回转部分最佳联接阻尼时间曲线

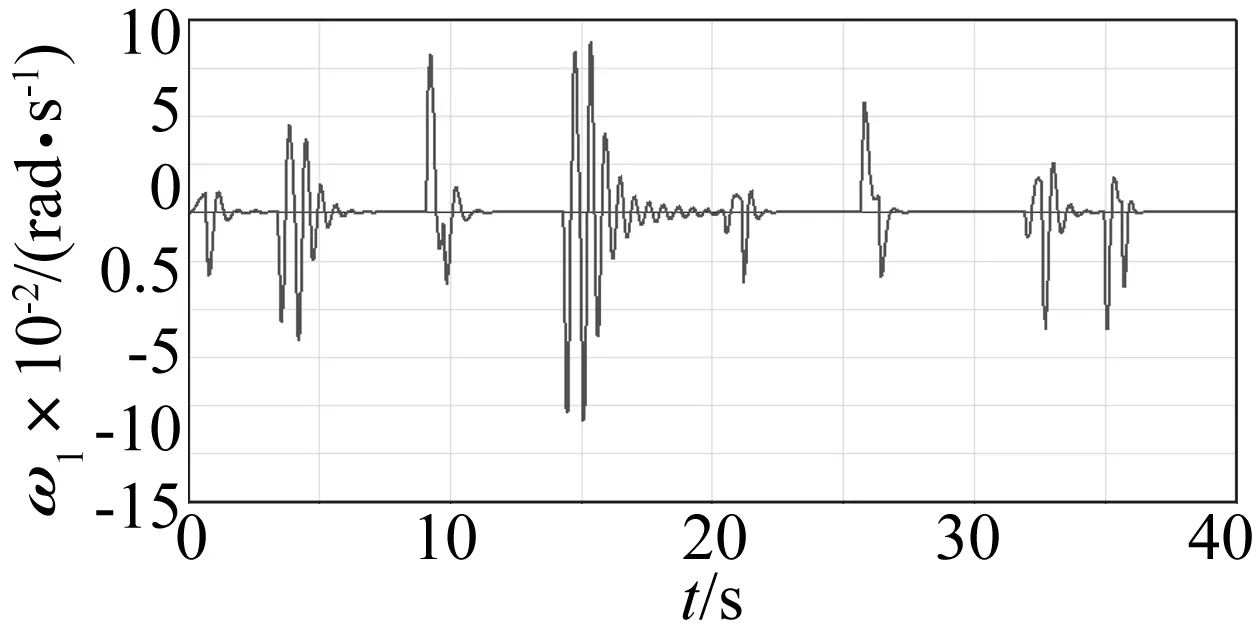
图9 发射架在高低平面内的角速度

图10 发射架在回转平面内的角速度

此外，发射架在高低和回转两个平面内的振动特性各不相同，在高低平面内的最大振动频率为1.9 Hz，采用的是振动衰减结束后发射的策略；而在回转平面内的最大振动频率为2.0 Hz，采用的是衰减到一定程度后发射的策略。

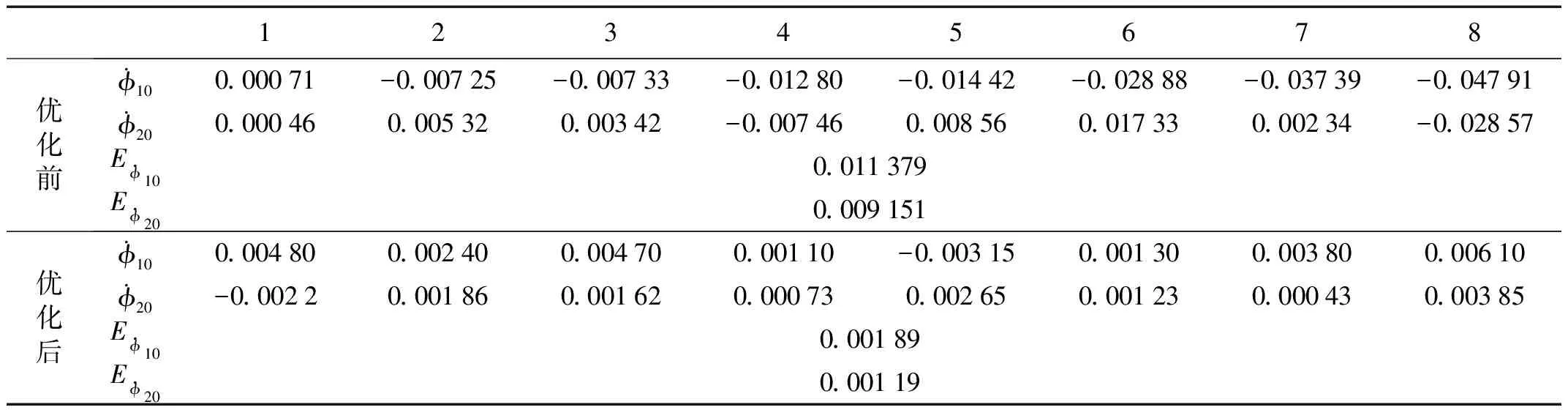
表1 初始扰动及中间偏差对比

由上述结果来看，造成发射架在两个平面内振动特性不一致的主要原因在于本优化研究是以保证系统整体初始扰动的中间偏差值为目的，而非保证单发射击精度为目的。因此，本优化分析结果对提高火箭炮系统的整体射击精度具有现实指导意义。

4 发射时间的随机性分析

根据发射实验统计，由于电子点火线路以及机械机构等因素，造成火箭弹的点火时间有一定的提前或延迟，提前或延迟的时间一般在±20e-3s以内。为有效分析发射时间随机性对初始扰动的影响，采用前述所建立的优化模型，并植入Monte Carlo分析方法，定义8个随机输入变量，它们分别是第一枚弹到第八枚弹的不同发射时间值(优化后)，输入变量的随机分布函数选用正态分布(Normal)函数，响应变量仍然是连射状况下火箭弹初始扰动的中间偏差Eφ0，设定最大分析次数为400次。

分析结果表明，响应变量值随着输入变量的随机取值而呈现很大随机性，其结果的平均值为0.004 596 54，标准偏差为0.002 074 56，由此可见发射时间的随机性对连射情况下火箭弹初始扰动的中间偏差有着很大的影响。图11所示为各个因素及其相互交叉对目标函数的影响程度分析结果，从中可以得出影响初始扰动中间偏差的因素比较复杂，几乎各个因素及其交叉因素对初始扰动中间偏差的影响都不占主导地位，相比较而言，因素T1(第一枚弹的发射时间)与T4(第四枚弹的发射时间)的交叉作用对初始扰动中间偏差的影响最大，影响程度约占到8.5%。因此，在轻型共架远程火箭炮设计电子点火器时要尽量保证因素T1与T4的点火精度。

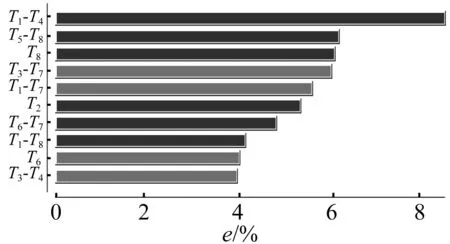
图11 初始扰动中间偏差灵敏度分析

5 结 论

本文在某型火箭炮的发射动力学模型中引入多岛遗传算法并开展了相应的优化研究，得到了一些有用的结论。

(1)从全文的研究过程和最后的仿真结果可以表明，所采用地在动力学模型基础上引入优化算法的方法是可行的，为其它系统的动力学优化分析提供方法借鉴。

(2)火箭弹在发射过程中，采用不等时隔连续发射所引起的系统初始扰动量要明显优于等时隔连续发射。优化表明，第一枚弹在零时刻发射之后的每一枚弹的最佳发射时间分别为：3.439 9，9.085 0，14.340 0，20.457 4，25.691 5，31.922 0，34.981 3(单位：s)。

(3)得出了不等时隔连续发射下起落部分、回转部分连接刚度和连接阻尼最佳匹配组合，为火箭炮主动减振装置设计和改造提供理论依据。

(4)分析了发射时间随机性对初始扰动的影响，结果表明发射时间的随机性对连射情况下火箭弹初始扰动的中间偏差有着很大的影响。但是各个因素及其交叉因素的影响都不占主导地位，相对而言，因素T1与T4的交叉作用对初始扰动中间偏差的影响最大。

[1]芮筱亭,王国平,陆毓琪.提高多管火箭射击密集度新技术[J].兵工学报,2006,27(2):301-305.

RUI Xiao-ting,WANG Guo-ping，LU Yu-qi.A new technology to improving firing dispersion of multiple launch rocket system[J].Journal of Acta Armamentari I，2006,27(2):301-305.

[2]陈兵,马大为,陈飞.使用BP网络和自适应遗传算法的某型火箭炮变发射间隔研究[J].兵工学报,2007,28(11):1287-1292.

CHEN Bing,MA Da-wei,CHEN Fei.Research on variable firing interval of certa in rocket launcher using bP neural net work and improved ada ptive genetic algorithm[J].Journal of Acta Armamentari I，2007,28(11):1287-1292.

[3]贺北斗,林永明,曹听荣.火箭发射装置设计[M].北京: 国防工业出社,1988

[4]冯勇，马大为，薛畅,等.多管火箭炮刚柔耦合多体发射动力学仿真研究[J].兵工学报,2006,27(3):545-548.

FENG Yong，MA Da-wei，XUE Chang，et al.Simulation studies of coupled rigid and flexible multi-body dynamics for multiple launch rocket systems[J].Journal of Acta Armamentari I，2006,27(3):545-548.

[5]冯勇,马大为,宋晓峰,等.某箱式火箭炮电液伺服系统交互式仿真研究[J].兵工学报,2006,27(2):363-366.

FENG Yong，MA Da-wei，SONG Xiao-feng，et al.Interactive simulation of electronic and hydraulic servo System about clustered canister rocket launching platform[J].Journal of Acta Armamentari I，2006,27(2):363-366.

[6]洪嘉振.多体系统动力学——理论、计算方法和应用[M].上海 :上海交通大学出版社，1992 .

[7]张思才,张方晓.一种遗传算法适应度函数的改进方法[J].计算机应用与软件,2006,23 (2):108-110.

ZHANG Si-cai,ZHANG Fang-xiao.A modified method to fitness function of genetic algorithms[J].Computer Application and Soft-ware，2006,23 (2):108-110.

[8]金晶,苏勇.一种改进的自适应遗传算法[J].计算机工程与应用,2005,42 (18):64-69

JIN Jing，SU Yong.An improved adaptive genetic algorithm[J].Computer Engineering and Application，2005,42 ( 18): 64-69.