总体最小二乘正则化算法的载荷识别

张 磊，曹跃云，杨自春，何元安

(1.海军工程大学 动力工程学院，武汉 430033；2.中国船舶工业集团公司 船舶系统工程部，北京 100036)

机械设备作用在支撑结构上的激励力，作为结构的动载荷。在结构动力响应计算、动态设计、故障分析及振动传递路径分析等领域，它都是需要预先掌握的能反映设备特性的重要参数。激振力可以通过力传感器直接测量，但因为力传感器尺寸和安装条件会受到限制，而且嵌入力传感器必将改变原有系统的动力特性，测量结果常出现偏差[1]。

因载荷直接测量有困难，载荷识别方法受到了重视并有大量成果出现[2]。载荷识别是已知系统响应和系统特性求激励特性的问题，是动力学第二类反问题。由于结构的模态特性，载荷反演问题中结构矩阵求逆的过程往往是病态的，该病态问题的恰当处理是载荷识别成功的关键，国内外许多学者对此做了许多有意义的工作。Thite等[3-4]提出逆矩阵法来识别工作载荷，利用最小二乘的正则化方法(Tikhonov正则化和奇异值截断方法)解决频率响应矩阵存在的病态问题，并讨论正则化参数选取(L曲线法、OCV法、GCV法)对载荷识别结果的影响。毛玉明[5]通过精细计算法建立精确的动态载荷识别问题反演模型，并引入正则化技术寻求一稳定近似解。姜菊萍等[6]利用多项式加速迭代法的正则化方法来解决振源重构中的不适定性。

上述最小二乘(Least Squares，LS)正则化方法在载荷识别时仅考虑振动响应误差的影响，当振动响应和传递函数矩阵同时受误差影响时，此类方法的载荷识别结果将含有较大误差，这时总体最小二乘(Total Least Squares，TLS)正则化算法将是一个最佳的选择。Liu 等[7]提出截断TLS正则化算法实现载荷识别，该算法既能考虑结构响应的误差也能反应频响函数矩阵的误差，载荷识别效果好。但其难以准确确定截断阈值，且容易截掉可靠的信息，导致解的分辨率下降。近些年，对TLS问题的研究逐渐深入和广泛。尽管TLS正则化算法在处理病态问题时存在一定的不足，但学者们[7-10]通过实例验证了当系数矩阵存在误差时，其解的精度要大大优于LS正则化算法。可见，非常有必要对TLS正则化算法进行改进，克服在实际应用中存在的不足，提高其处理病态问题的有效性和鲁棒性。笔者将围绕迭代TLS正则化算法在载荷识别中的应用展开深入研究。

1 最小二乘法的载荷识别

若一线性时不变结构，有激励F1，F2，…Fm，时，存在响应b1，b2，…，bn，由系统的运动方程可得[7]

bn=Hn×mFm

(1)

式中:Hn×m为传递函数矩阵(频率响应函数矩阵)，Fn为路径载荷的频域力列向量，bm为频域参考点响应信号的列向量。

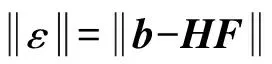
(2)

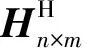
2 CG-TLS正则化算法的载荷识别

载荷识别时，由于结构的模态特性以及响应测点选取等问题，传递函数矩阵中包含的结构信息存在很大的相似性，导致各列之间复共线性强，传递函数矩阵为病态。无论是直接逆矩阵法估算激励力还是最小二乘估计激励力，都无法避免病态矩阵所带来的计算误差。本节将在TLS的基础上进行Tikhonov正则化，构造出目标函数，然后利用共轭梯度(Conjunction Gradation，CG)法求解该目标函数的最优化问题。建立一种能同时考虑振动响应点和传递函数矩阵受误差影响且速度快、精度高、鲁棒性好的CG-TLS正则化算法，最终实现载荷识别。

2.1 TLS正则化算法

总体最小二乘问题的准则为

(3)

满足b0=H0x，x代表式(1)中的激励力F。当H0=H时，不考虑系数矩阵的误差，此时TLS准则等效于LS准则。

将式(3)进行Tikhonov正则化，得到以下的目标函数

(4)

式中:E为系数矩阵的误差，r为观测向量的误差。λ为正则化参数，决定着解分辨率和光滑性这对不可调和的矛盾能否达到最佳折衷，同样掌握着病态问题求解过程成功与否的命运。矩阵Li为正则化矩阵，一般为带状行满秩矩阵，经典定义为单位矩阵，也可表示为权值的对角矩阵或者差分运算[11]。

构造拉格朗日目标函数

(5)

(6)

(7)

(H+E)x=b+r

(8)

将式(7)代入式(6)有:

E=-rxH

(9)

结合式(9)和式(8)可推出:

将r和E带入目标函数式(4)，得到新的目标函数为:

(10)

依据上式，f(x)的一阶导数为

g(x)=f(x)=

(11)

可见，式(10)为无约束的最优化问题，但该函数的凹凸性未知。Beck等[9]提出信赖域方法求解此最优问题。Lampe[10]首先建立了高斯-牛顿迭代法进行该最优化问题的求解，但需满足函数f(x)二阶导数为正定，此假设一般情况不易满足。为提高算法的求解速度，文献[12]利用正交投影法，建立基于Krylov子空间的迭代TLS算法。上述方法不同程度上存在数值性能表现不佳、算法繁琐，且在每步迭代时需要的存贮量和计算量较大，也不易达到全局收敛等不足。

2.2 CG-TLS正则化算法

共轭梯度法[13]在处理此类优化问题时因其算法简便、所需存储量小、收敛速度快等特点而受许多研究人员所关注，各种各样的非线性共轭梯度法如雨后春笋般的不断涌现。但现存的方法大都存在一些不足，如数值稳定性不佳，全局收敛的条件苛刻等。本节引入一种能解决非凸目标函数，在特定线性搜索条件下易全局收敛的鲁棒性好的非线性共轭梯度法。

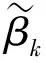
为使算法能较迅速地收敛到最优解，利用重新开始技术[16]改进共轭梯度法，改进思想为：若迭代到距离最优点比较近时，重新取搜索方向为负梯度方向，随后的几次迭代将产生近似的共轭方向，从而提高算法的效率。一般在实际应用中每迭代l或l+1次，就重新设定搜索方向为负梯度方向，得到l步重新开始的共轭梯度法。优化问题式(10)求解程序如下

程序1：

Step0 给定迭代精度0<ε≪1(取ε=10-6)和初始点x0，计算g0=f(x0)，令k∶=0。

Step 2计算搜索方向dk：

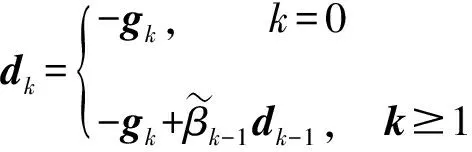
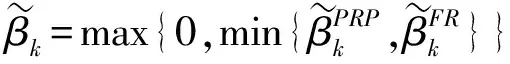
Step 5 令k∶=k+1，转向步骤Step1。

2.3 正则化参数和正则化矩阵选取

3 仿真验证

为检验第2节中提出的CG-TLS正则化算法在处理载荷识别不适定问题中的实际效果。通过ansys仿真一钢质平板在四个激励力作用下的响应，据此进行载荷识别算法验证。仿真的优势在于精确激励力为已知，且可以更灵活、全面地进行算法的评估。

仿真钢质矩形板尺寸为600 mm×500 mm×6 mm，密度为7 800 kg/m3，泊松比为0.3，阻尼系数为0.1，受四个垂直钢板的激励力作用，有限元模型如图1所示，随机布置10个响应点(包含动载荷信息较为丰富的测点，且振动响应不雷同的测点)。仿真中，动载荷F1，F2，F3，F4为整个频带内的单位激励，激励频率范围为10～1 000 Hz。经计算得到钢质板的前十阶模态为(14.146 Hz，28.281 Hz，31.872 Hz，38.522 Hz，67.279 Hz，73.629 Hz，76.154 Hz，97.613 Hz，121.660 Hz，126.820 Hz)。对每个激励点单独激励，经10次平均，依据激励力和响应点的加速度响应，计算得到传递函数矩阵Hn×m，n为响应点的数目，m为激励力的数目。传递函数矩阵Hn×m的病态与否直接影响载荷识别的效果，一般情况下，由于结构的模态效应，响应点之间具有一定的相关性。尤其在低频时，响应由单个模态或较少模态叠加而成，相关性更强。这使得Hn×m包含的结构信息存在很大的相似性，将直接导致传递函数矩阵病态，低频段病态性更严重。为减轻Hn×m的病态性，通常选择n>m，但经分析表明n>m并不一定能避免Hn×m病态，若选择不当反而会放大矩阵的病态性。

为了有效避免矩阵Hn×m病态，需首先诊断矩阵的病态性，利用条件数法和特征值分析法进行病态性的诊断[17]。不同响应点组成的Hn×m其矩阵的条件数和特征值不同，从10个备选响应点中选择4个最佳响应点组成Hn×m(最佳响应点即在整个频率范围内条件数均较小，且特征值分布适宜)，进而得到具有较轻病态性的Hn×m。即使如此，某些频率点处对应的Hn×m矩阵仍为病态矩阵，对其进行求逆会出现不稳定，又由于观测噪声不可避免，将导致载荷识别精度变差，结果不可信。正则化算法作为一种解决此类不适定问题的有力工具，本节将讨论基于LS的Tikhonov算法[4]、TTLS算法[7]、CG-TLS正则化算法在载荷识别中的适用性。

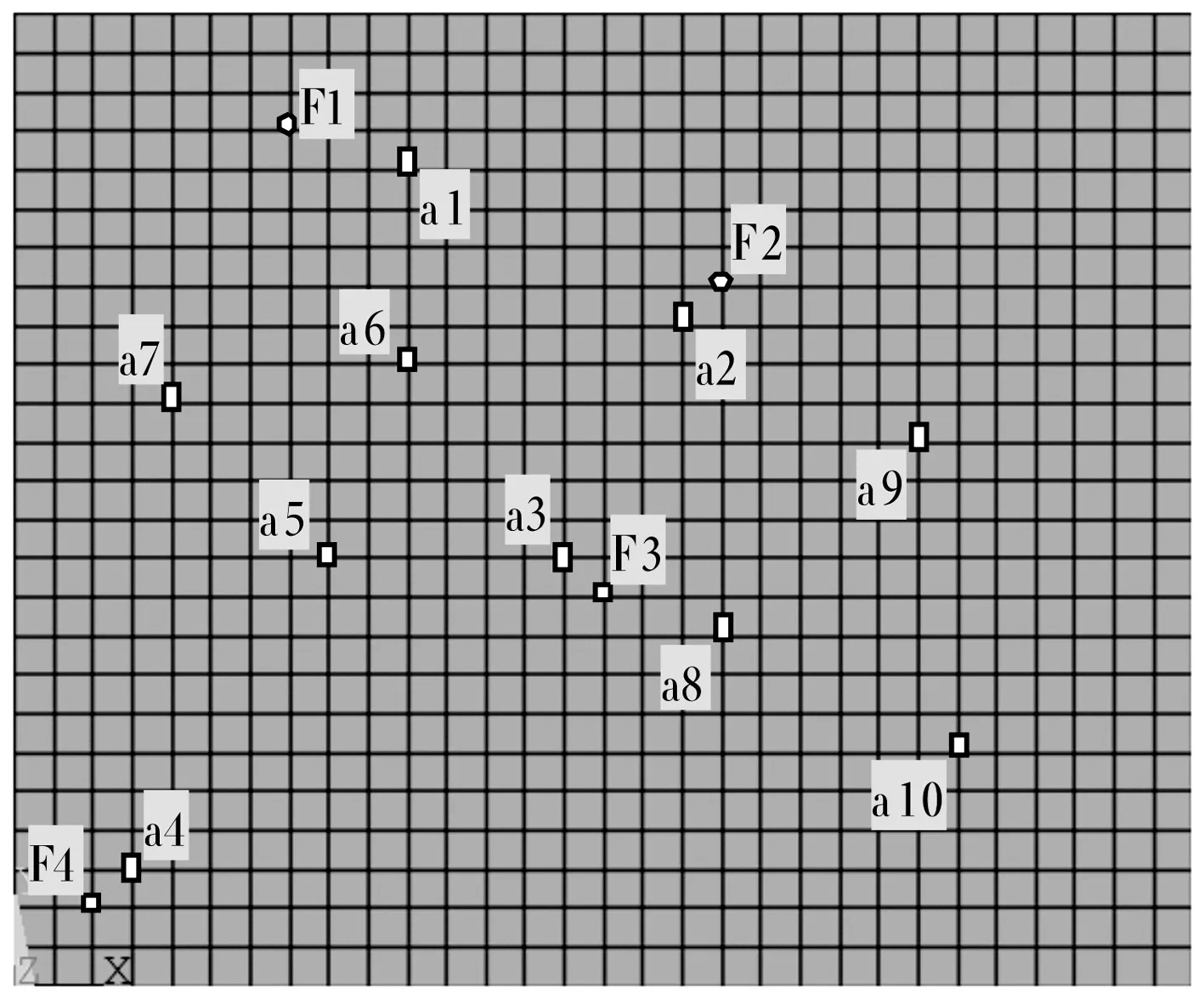
图1 有限元模型

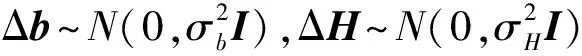
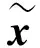
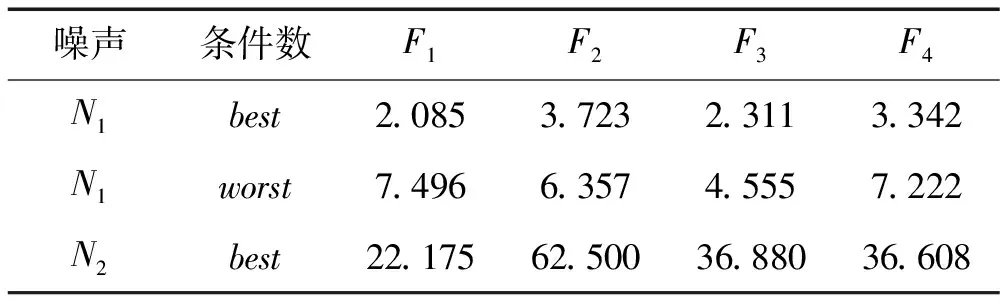
表1 激励力偏差范数结果表

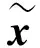
图2 条件数比较图

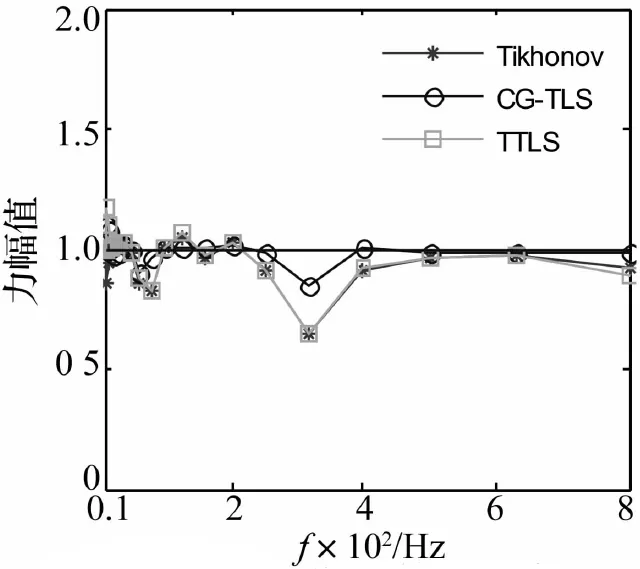
图3 噪声N1时计算激励力F1的1/3倍频程图

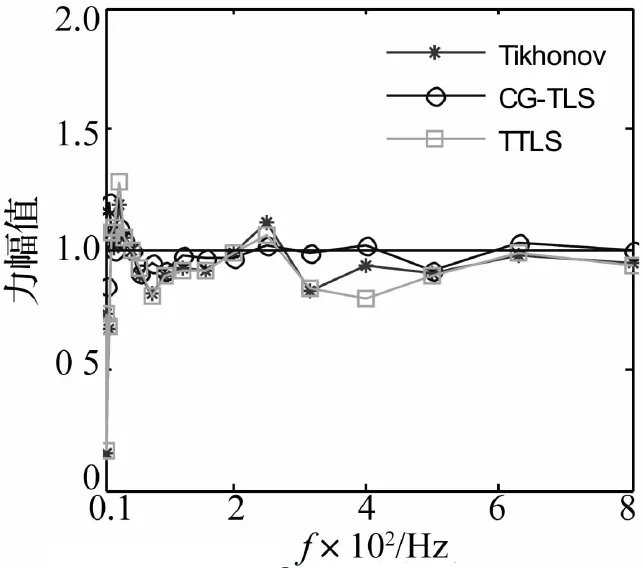
图4 噪声N1时计算激励力F3的1/3倍频程图

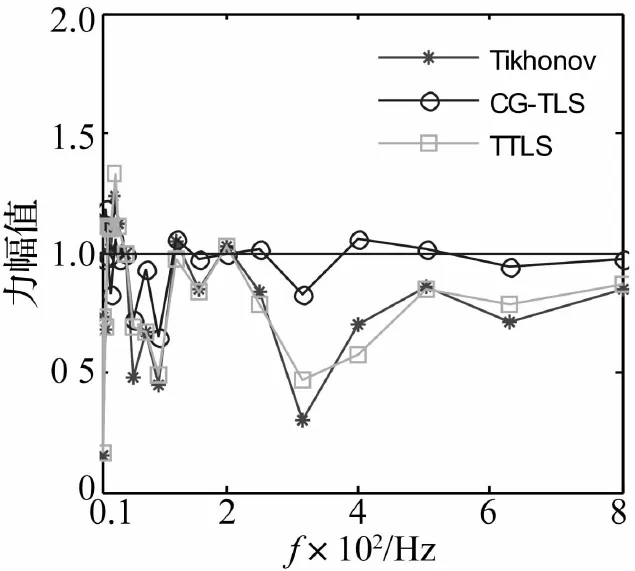
图5 噪声N2时计算激励力F1的1/3倍频程图

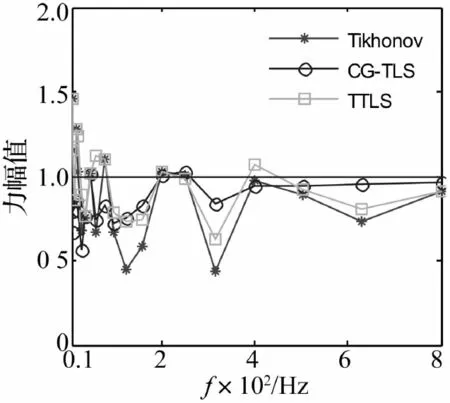
图6 噪声N2时计算激励力F3的1/3倍频程图

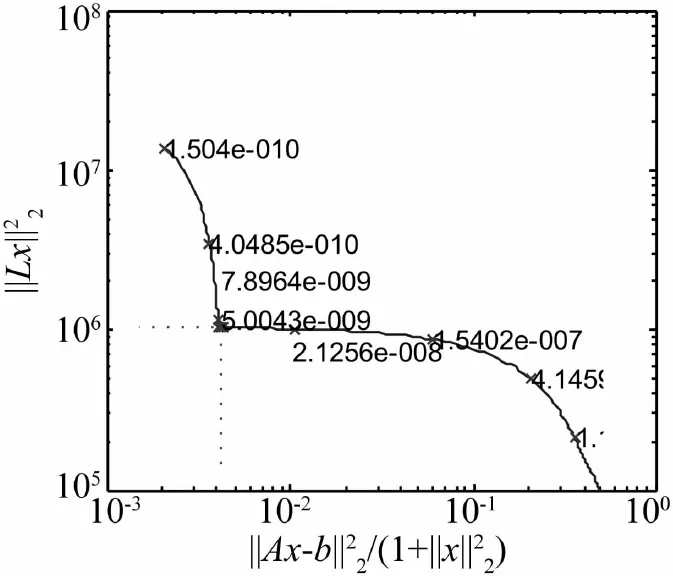
图7 L曲线图

保持加速度响应噪声水平σb不变，将传递函数矩阵的噪声水平提高到N2，计算得到图5、图6为F1和F3激励力的三分之一倍频程图。可见，随着传递函数矩阵噪声水平的提高，Tikhonov正则化算法计算结果急剧变差，而TLS正则化算法对噪声的考虑较全面，载荷识别精度高于前者。在某些频点处，TTLS算法反而精度不高，可能由于处理矩阵维数较小，易截掉有价值的信息，而且奇异值的逐渐下降分布导致截断阈值难以准确确定。CG-TLS算法受噪声水平和频响函数矩阵奇异性的影响最小，计算精度高于以上两种算法，表2给出了同样的结论。因此，CG-TLS算法在进行载荷识别时具有较好的有效性和鲁棒性。

表2 激励力偏差范数结果表

4 试验验证

本节引入某双层圆柱壳体的振动激励-响应试验，进一步检验CG-TLS正则化算法在载荷识别中的有效性。试验细节祥见文献[18]，试验存在三个激励源，在内壳体上合理布置若干振动加速度计。选择激励工况为1#、2#、3#激振器分别单独开启和同时开启，且均发射连续的正弦信号，频率为3 kHz，功率输出均为92 vpp。在进行传递函数矩阵估计时，采用多次激励，做了6次平均来尽量减少噪声信号的污染。

为准确求取工作载荷，需首先选取恰当的振动响应点组成较为良态的传递函数矩阵，依据第3节中指出的条件数和特征值分布诊断方法，确定最佳的响应点组合为振动传感器(2，6，8，10)(具体位置见文献[18]中的图3)。计算传递函数矩阵的条件数，在3 kHz时矩阵的条件数为3.716×104，存在严重病态。在该频点处，利用正则化算法提高载荷识别的精度，CG-TLS算法的迭代初始值选为(0，0，0)，L曲线法确定正则化参数如图7所示。各种正则化算法的计算结果见表3，表中用激励力估计值与其真值的差值范数衡量算法的计算精度。结果表明：经正则化算法修正的载荷识别精度有显著的提高，因试验中随机噪声和测量误差不可避免，使得传递函数矩阵和振动加速度响应的观测项存在误差波动，CG-TLS正则化算法可以有效地减轻此类误差波动对载荷识别的影响，在保持计算效率的同时提高了载荷识别的精度。CG-TLS正则化算法计算值与真值的误差可能源于：数据处理伴随的数值计算误差；频域处理时的加窗截断导致频率泄露，从而降低了解的分辨率；利用离散数据的傅里叶变换结果始终不如连续傅里叶变换的结果好。

表3 激励力的计算结果表

5 结 论

载荷识别的间接法，是动力学的第二类反问题，实际操作过程中常出现求解不适定问题，且主要表现在病态矩阵求逆的不稳定性。为克服上述问题，结合共轭梯度法建立的CG-TLS正则化算法，具有算法简便、所需存储量小、收敛性能好等优点，且能同时考虑传递函数矩阵和振动响应受噪声影响，更符合载荷识别的实际情况。

仿真结果表明结构模态特性(尤其低频情况)以及响应点的组合形式是导致传递函数矩阵病态的根源,依据条件数和特征值分布优选响应点组合，能减轻传递函数矩阵的病态性的影响，进而提高载荷识别的精度。正则化条件下，载荷识别的性能优于直接计算法，CG-TLS正则化算法与真实值吻合非常好，优于Tikhonov正则化、TTLS算法，并且具有较低的噪声灵敏度和对迭代初始值不敏感性等优点。振动激励-响应试验进一步肯定了以上结果，并指出可能产生误差的原因为数值计算误差，频率泄露或离散数据傅里叶变换。综上，CG-TLS正则化算法能够减轻误差波动对载荷识别精度的影响，在提高效率和抗噪能力的同时保证了载荷识别的精度。

[1]原春晖.机械设备振动源特性测试方法研究[D].武汉：华中科技大学，2006.

[2]Mohammed H F，Mohd J M，Ahmad K A，et al.Inverse combustion force estimation based on response measurements outside the combustion chamber and signal processing[J].Mechanical Systems and Signal Processing，2009，23: 2519-2537.

[3]Thite A N，Thompson D J.The quantification of structure-borne transmission paths by inverse methods.Part 1: Improved singular value rejection methods[J].Journal of Sound and Vibration，2003(264): 411-431.

[4]Choi H G，Thite A N，Thompson D J.Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J].Journal of Sound and Vibration，2007(304): 894-917.

[5]毛玉明.动载荷反演问题时域分析理论方法和试验研究[D].大连：大连理工大学，2010.

[6]姜菊萍，姜哲.利用迭代正则化法重构振动声源[J].噪声与振动控制，2006,26(5)：34-36.

JIANG Ju-ping，JIANG Zhe.Vibrating resources reconstruction using iterative regularization[J].Noise and Vibration Control，2006,26(5)：34-36.

[7]Liu Y，Steve W，Shepard J.Dynamic force identification based on enhanced least squares and total least-squares schemes in the frequency domain[J].Journal of Sound and Vibration，2005(282): 37-60.

[8]Maziar S，Hossein Z.Computational experiments on the tikhonov regularization of the total least squares problem[J].Computer Science Journal of Moldova，2009，17(1): 14-25.

[9]Bech A，Ben-Tal A.On the solution of the tikhonov regularization of the total least squares problem[J].SIAM Journal Optimal，2006，17: 98-118.

[10]Lampe J.Solving regularized total least squares problems based on eigenproblems[D].Hamburg: Hamburg University of Technology，2010.

[11]Wang Y M，Liang G B，Pan Z D.Inverse of particle size distribution from light-scattering date using a modified regularization algorithm [J].Particuology，2010，8: 365-371.

[12]Lampe J，Voss H.Large-scale tikhonov regularization of total least squares[J].Journal of Computational and Applied Mathematics，2013，238: 95-108.

[13]戴彧虹，袁亚湘.非线性共轭梯度法[M].上海：上海科学技术出版社，1994：1-27.

[14]魏志强，张愿章.复共轭梯度法的结构[J].哈尔滨理工大学学报，2012，17(4): 122-126.

WEI Zhi-qiang，ZHANG Yuan-zhang.Structure of the complex conjugate gradient method[J].Journal of Harbin University of Science and Technology，2012，17(4): 122-126.

[15]Liu H L.A family of nonlinear conjugate gradient methods with a global convergence property[J].International Journal of Number Methods and Applications，2009，2: 81-87.

[16]解可新，韩健，林友联.最优化方法[M].天津：天津大学，1998：22-24，110-120.

[17]卢秀山.Ⅱ类病态系统分析理论及其应用研究[D].青岛：山东科技大学，2006.

[18]张磊，曹跃云，杨自春，等.双层圆柱壳体水下振动噪声结构传递路径分析[J].振动与冲击，2012，31(20)：12-16.

ZHANG Lei，CAO Yue-yun，YANG Zi-chun，et al.Structural transfer path analysis for vibration and noise of a submerged cylindrical double-shell[J].Journal of Vibration and Shock，2012，31(20)：12-16.