应变率对钢筋混凝土框架结构地震作用下灾变过程影响研究

王文明， 李宏男， 王德斌， 尚 兵

(1.大连理工大学 建设工程学部，辽宁 大连 116024；2.清华大学 航天航空学院，北京 100084)

钢筋和混凝土都有一定的率敏感性，在不同应变率下，具有不同的力学性能。试验研究表明[1-6]，钢筋和混凝土的本构关系均随着应变率的改变而改变。在地震作用下，混凝土的应变率一般能达到10-3/s～10-2/s量级，最大能达到10-1/s左右[3]，钢筋能达到的应变率更大。对结构进行抗震分析时，采用静态力作用下的计算理论不尽合理，应该考虑材料的应变率效应。

钢筋混凝土框架结构是一种应用极为广泛的结构形式，在国内外的历次地震中，这种结构发生破坏或倒塌的现象时有发生。因此，研究应变率对钢筋混凝土框架结构在地震作用下灾变过程的影响具有重要意义。国内外一些学者研究了材料的应变率效应对钢筋混凝土框架结构地震作用下非线性响应的影响[7-8]。然而，目前研究中采用的本构关系不尽合理、分析工况偏少，且缺乏应变率对结构极限状态和倒塌阶段影响的研究。

ABAQUS有限元分析软件具有强大的非线性分析功能，但是该软件缺乏简化实用的既能用于混凝土，又能用于空间梁单元的本构模型[9]。基于《混凝土结构设计规范》(GB 50010-2010)[10]，开发了适用于显式算法、可以用于空间梁单元的用户材料子程序。该子程序可以用于传统的非线性时程分析，也可用于结构的连续性倒塌分析。采用开发的程序，通过对某四层钢筋混凝土框架结构进行增量动力时程分析，研究了材料的应变率效应对结构最大顶点位移、最大基底剪力、最大层间位移、能力曲线、抗倒塌能力和倒塌模式的影响。

1 ABAQUS用户材料子程序开发

1.1 混凝土的本构模型

混凝土的本构模型如图1所示(混凝土受拉、受压的应力-应变曲线示意图绘于同一坐标系中，但取不同的比例)。这里考虑了混凝土开裂应变和混凝土极限压应变：当应变超过开裂应变后，混凝土仍然具有抗压能力，但不再具有抗拉能力；当应变超过极限压应变后，单元不再具有承载能力。图1中的曲线为采用编制的程序，对素混凝土构件进行轴向拉压得到。极限压应变和开裂应变之间的部分与《混凝土结构设计规范》(GB 50010-2010)给出的曲线一致。

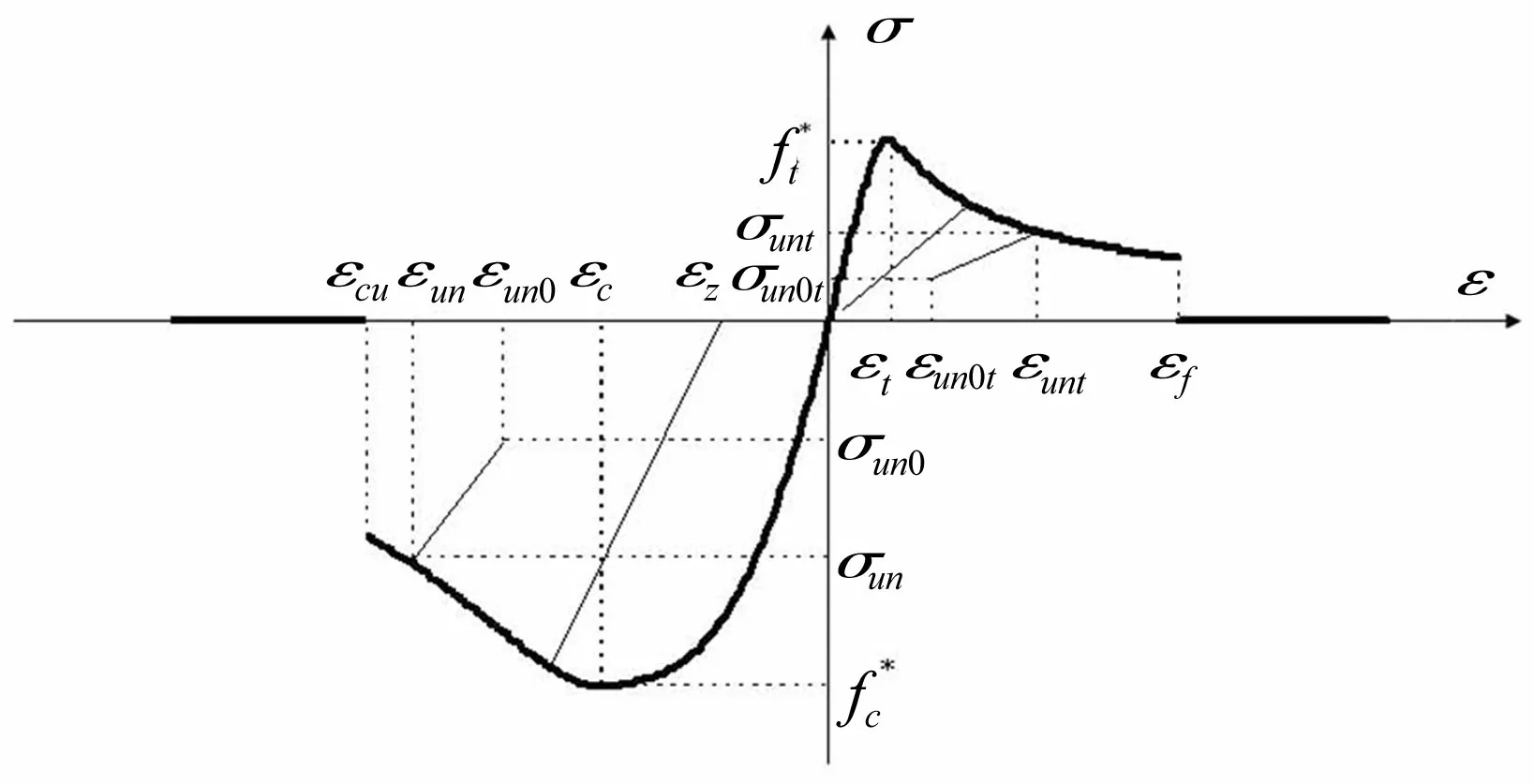
图1 程序编制采用的混凝土应力-应变关系

混凝土受压的应力-应变曲线方程按下列公式确定：

(1)

εcu=0.003 3-(fcu,k-50)×10-5

(2)

(3)

(4)

(5)

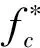
混凝土受拉的应力-应变曲线方程按下列公式确定：

(6)

(7)

(8)

(9)

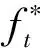
受压混凝土的卸载及再加载应力-应变关系按下式确定：

σ=Er(ε-εz)

(10)

(11)

(12)

(13)

式(10)～式(13)中：Er为割线模量；εz为受压混凝土卸载至零应力点时的残余应变；σun0和εun0分别为混凝土受压卸载曲线终点的应力和应变；σun和εun分别为受压混凝土从骨架曲线开始卸载时的应力和应变；εca为附加应变。

受拉混凝土的卸载及再加载应力-应变关系按下式确定：

σ=Ert(ε-εz)

(14)

(15)

式(14)～式(15)中：Ert为割线模量；σun0t和εun0t分别为混凝土受拉卸载曲线终点的应力和应变；σunt和εunt分别为受拉混凝土从骨架曲线开始卸载时的应力和应变。

1.2 钢筋的本构模型

钢筋采用理想弹塑性本构模型，如图2所示。当钢筋的应变超过极限应变时，单元不再具有承载能力。

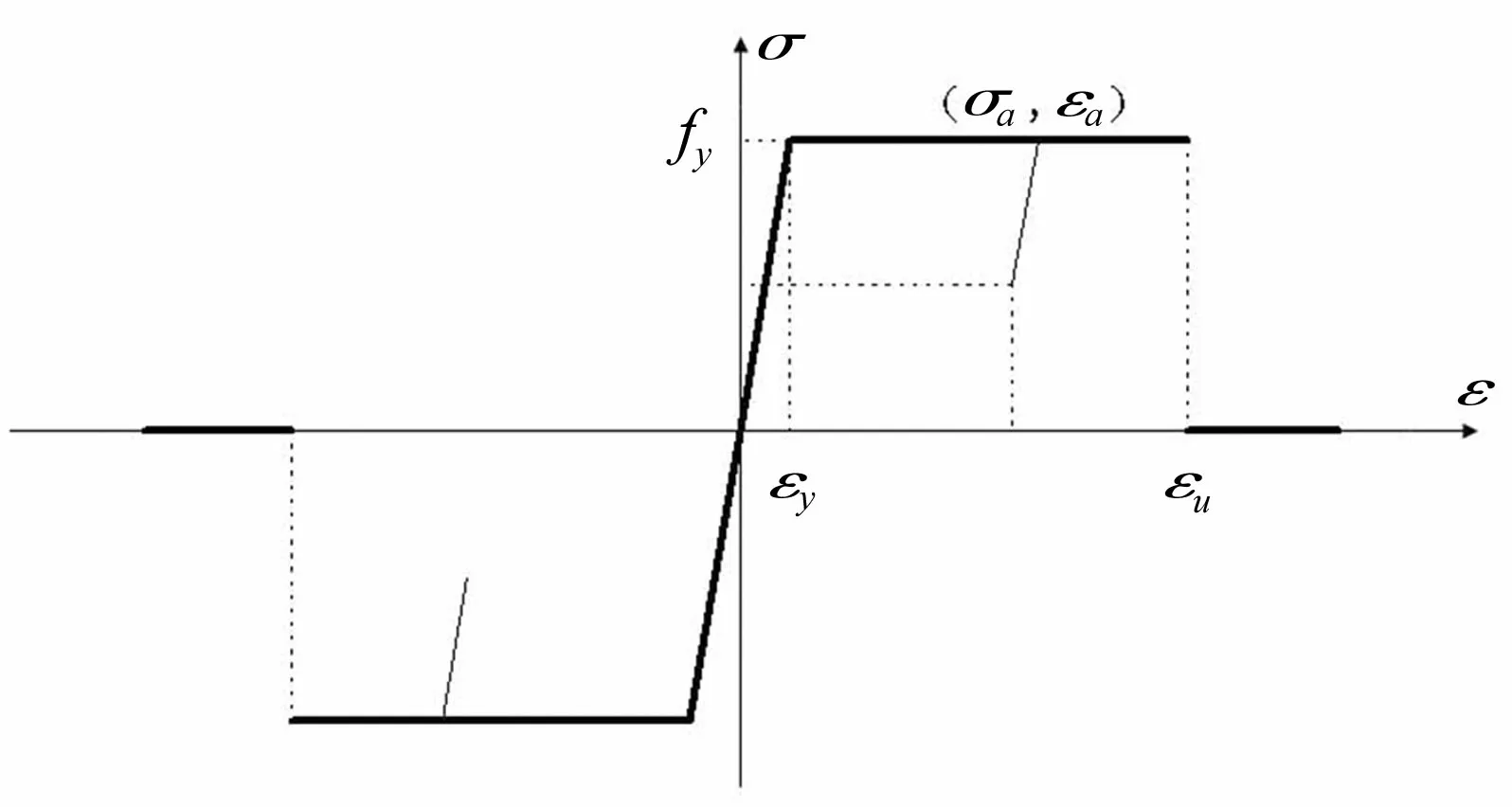
图2 钢筋的应力-应变关系

钢筋单调加载应力-应变曲线关系按下式确定：

(16)

εu=40εy

(17)

式(16)～式(17)中：Es为钢筋的弹性模量；εy为钢筋的屈服应变；fy为钢筋的屈服强度；εu为钢筋的极限应变，数值可根据试验数据选取，也可根据式(17)计算。

钢筋反复加载应力-应变关系按下列公式确定：

σ=σa+Es(ε-εa)

(18)

式中：σa为卸载点的应力；εa为卸载点的应变。

1.3 材料的应变率效应

1.3.1 钢材的应变率效应

在地震作用下，钢材的应变率一般不会超过1 /s。对结构进行抗震分析时，普通建筑钢材的动态本构模型可采用李敏提出的模型[2]。在地震作用的应变率范围内，钢材的抗拉强度提高幅度很小，可以不予考虑。动态的屈服强度可按下式计算：

(19)

cf=0.170 9-3.289×10-4fys

(20)

1.3.2 混凝土的应变率效应

随着应变率的提高，混凝土的弹性模量和泊松比如何变化没有达成一致共识[4]，目前分析中可以不予考虑。随着应变率的提高，混凝土的抗压强度有明显的增加趋势。混凝土动态抗压强度可按下面的公式计算[5]：

(21)

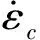
随着应变率的提高，混凝土的抗拉强度有明显的增加趋势。混凝土动态抗拉强度可按下面的公式计算[6]：

(22)

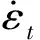
1.4 子程序的试验验证

下面通过试验对子程序的有效性进行验证。试验模型为一根钢筋混凝土框架柱，构件尺寸、柱截面尺寸及配筋和加载装置如图3所示。柱纵向受力钢筋为HRB335级钢筋，实测屈服强度为381.5 MPa。混凝土实测立方体抗压强度标准值为50.73 MPa。

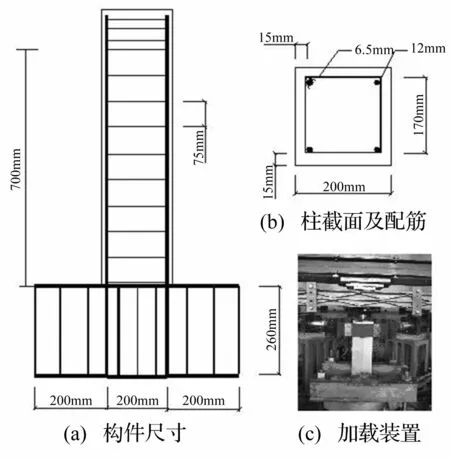
图3 试验概况

沿构件的轴线方向施加恒定的轴力，轴压比为0.05。加载方式为单方向单调加载，采用位移控制的方法，拟静力加载速率为0.1 mm/s，动力加载速率为40 mm/s。试验结果和数值模拟结果如图4所示。可以看出，数值模拟结果与试验结果吻合较好，验证了开发程序的可靠性。

2 结构模型与参数选取

分析模型为四层钢筋混凝土框架结构，结构的三维有限元模型如图5所示，结构的尺寸及配筋如图6所示。结构每层的质量为318 630 kg，结构构件之外的质量添加到楼板上。钢筋采用HRB335，混凝土采用C30，材料强度取标准值。梁、柱材料的本构模型均采用编制的子程序，不考虑楼板的材料非线性。钢筋的性能参数如表1所示，混凝土的性能参数如表2所示。

图4 试验结果和数值模拟结果对比

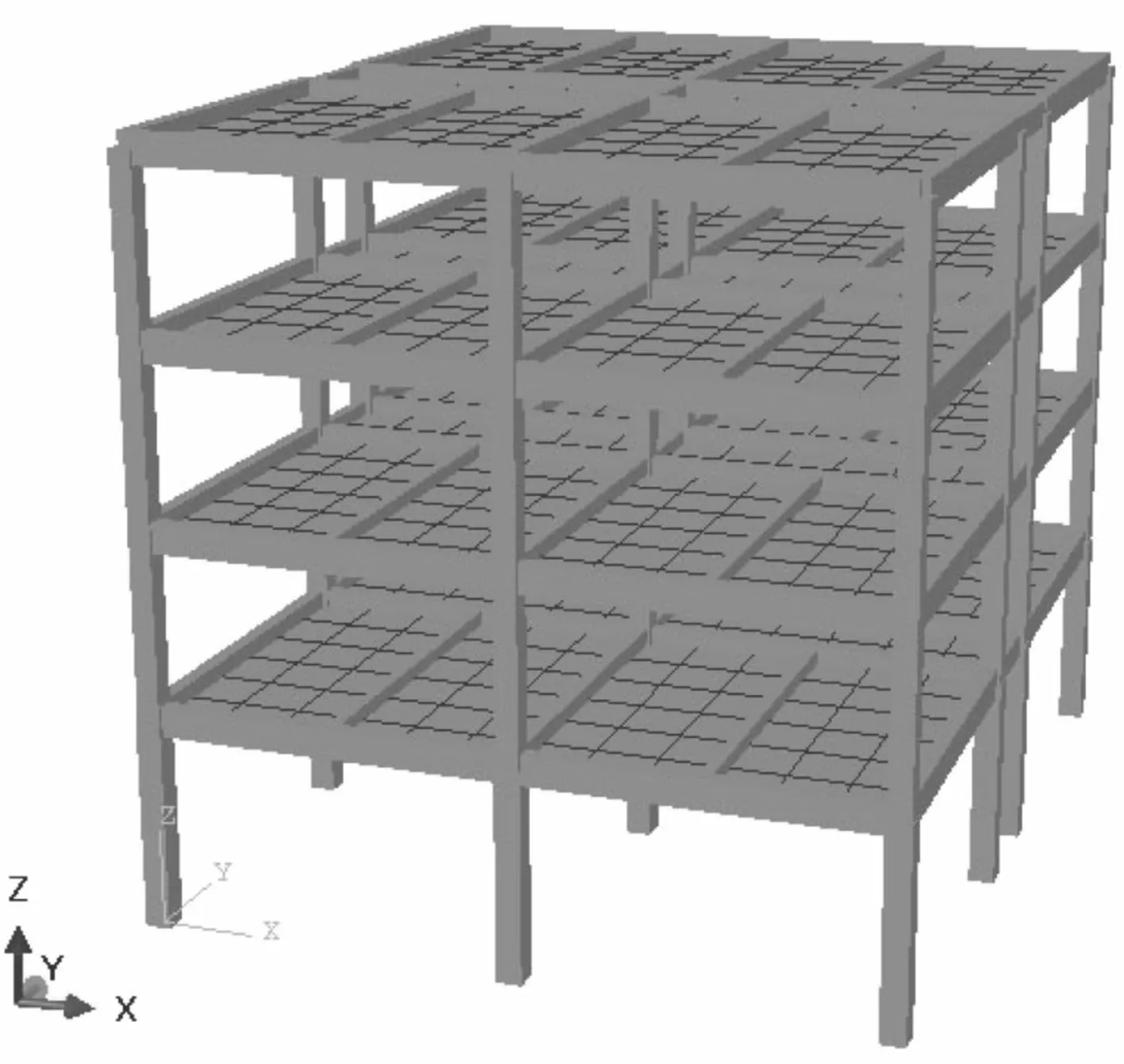
图5 结构三维有限元模型

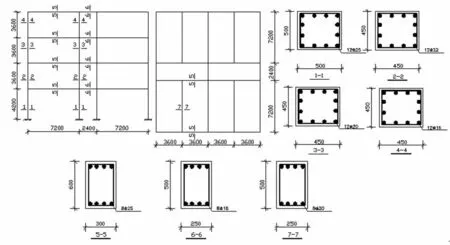
图6 结构尺寸及配筋图(单位：mm)

表1 钢筋的性能参数

表2 混凝土的性能参数

结构前三阶振型分别为x方向平动、y方向平动和绕z轴的扭转，相应的周期分别为0.783 1 s、0.745 9 s和0.601 4 s。楼板采用S4R单元，楼板厚度为0.12 m。梁和柱采用B31单元，柱的单元尺寸为0.6 m，梁的单元尺寸为1.2 m，楼板的单元尺寸为1.2 m×1.2 m。

3 数值计算与分析

选取多组地震波，通过改变地震波的峰值加速度，对结构分别进行不考虑应变率和考虑应变率的增量动力时程分析。进行增量动力时程分析时，地震波三个方向的峰值加速度等比例增大，直到结构发生连续性倒塌为止。连续性倒塌的判别标准为，分析过程中，结构发生连续性倒塌，或者分析结束后，结构丧失了承受自身重量的能力。

3.1 选用的地震波

采用的地震波分别为：El Centro波(1940)、Taft波(1952)和天津波(1976)。每组地震波包含两个水平分量和一个竖向分量，竖向分量沿结构的Z向输入，峰值加速度较大的水平分量沿结构的Y向输入。El Centro波和Taft波的最大峰值加速度最小调幅到1 m/s2，天津波最小调幅到0.5 m/s2，每隔0.5 m/s2进行一次输入，直到结构发生连续性倒塌为止。

3.2 应变率效应对结构最大顶点位移的影响

结构在地震作用下的最大顶点位移如表3所示。由表中数据可以看出，随着地震波强度的增强，结构的最大顶点位移逐渐增大。对于所选的三组地震波，该结构对天津波更为敏感。这是由于，该结构基本周期与天津波的卓越周期较为接近。

在不同强度地震波作用下，考虑应变率后，结构x和y方向最大顶点位移相对改变量如图7所示。由分析结果可以看出，考虑材料的应变率效应后，结构的最大顶点位移可能增大，也可能减小。当地震波的强度较弱时，材料的应变率效应对结构最大顶点位移的影响很小，这是由于此时钢筋不能发生屈服，仅有混凝土的应变率效应起作用。随着地震波强度的增强，材料的应变率效应对结构最大顶点位移的影响有增大的趋势。当地震波增强到使结构接近于发生连续性倒塌时，材料的应变率效应能够使结构的最大顶点位移明显减小。

图7 最大顶点位移相对改变量

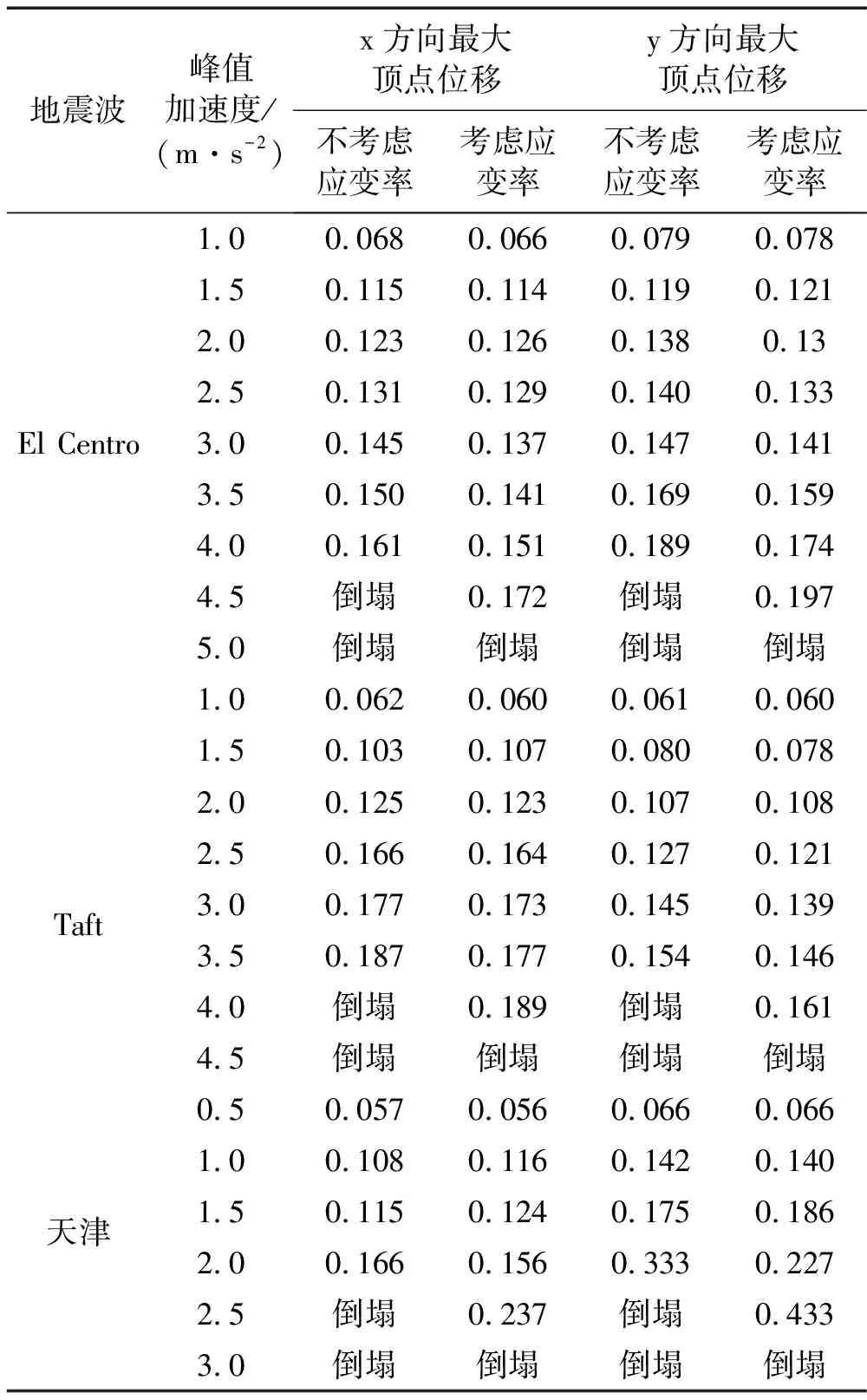
表3 结构的最大顶点位移

3.3 应变率效应对结构最大基底剪力的影响

结构在地震作用下的最大基底剪力如表4所示。由表中数据可以看出，随着地震波强度的增强，结构的最大基底剪力开始逐渐增大，后来可能增大可能减小。在不同强度地震波作用下，考虑应变率后，结构x和y方向最大基底剪力相对改变量如图8。由图中数据可以看出，考虑材料的应变率效应后，结构的最大基底剪力大多数情况下增大，也可能减小。当地震波的强度较弱时，材料的应变率效应对结构最大基底剪力的影响很小。随着地震波强度的增强，材料的应变率效应对结构最大基底剪力的影响有增大的趋势。

图8 最大基底剪力相对改变量

表4 结构的最大基底剪力

3.4 应变率效应对结构最大层间位移的影响

在三组地震波作用下，结构发生坍塌的位置均在第二层，第二层的最大层间位移如表5所示。考虑应变率后，结构第二层x和y方向最大层间位移相对改变量如图9所示。由分析结果可以看出，应变率对结构最大层间位移的影响规律与对最大顶点位移的影响规律类似，主要区别在于材料的应变率效应对结构最大层间位移的影响更为明显。这是由于结构的非线性变形主要集中在薄弱层，薄弱层材料的应变率较大，薄弱层受应变率的影响最大。

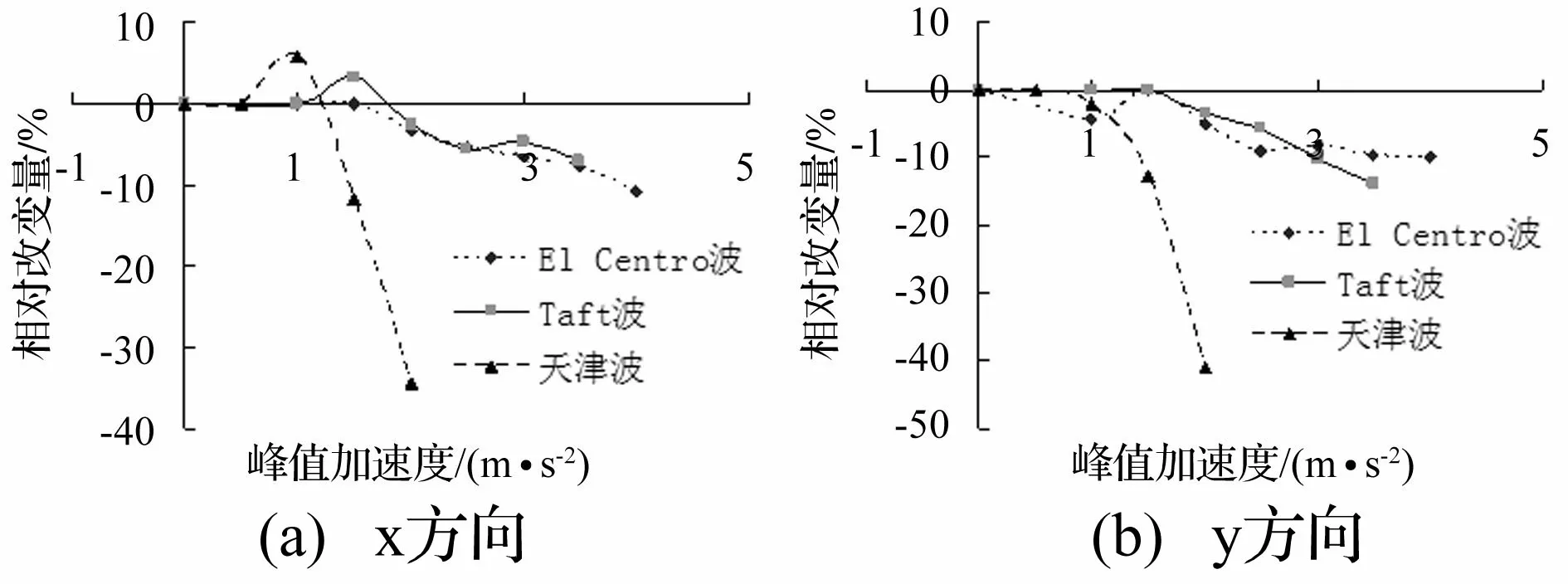
图9 最大层间位移相对改变量

表5 结构的最大层间位移

3.5 应变率对结构能力曲线的影响

通过增量动力时程分析，可以得到结构的能力曲线。通过该方法得到的能力曲线比通过pushover分析得到的结果更为准确，这里研究了材料的应变率效应对结构能力曲线的影响。结构在三组地震波作用下x方向的能力曲线如图10所示，y方向的能力曲线如图11所示。

由图中曲线可以看出，结构在不同地震波作用下的能力曲线明显不同。对比考虑应变率和不考虑应变率的曲线可以看出，考虑材料的应变率效应后，结构的能力曲线提高，但形状基本不变。

3.6 应变率效应对结构抗倒塌能力和倒塌过程的影响

对于El Centro波，考虑材料的应变率效应后，结构发生倒塌时的峰值加速度从4.5 m/s2提高到了5.0 m/s2；对于Taft波，结构发生倒塌时的峰值加速度从4.0 m/s2提高到了4.5 m/s2；对于天津波，结构发生倒塌时的峰值加速度从2.5 m/s2提高到了3.0 m/s2。在三组地震波作用下，考虑材料的应变率效应后，结构可以承受的峰值加速度均提高了0.5 m/s2。可以看出，结构的抗倒塌能力有一定程度的提高。结构的抗倒塌能力提高的原因在于：考虑材料的应变率效应后，材料的特征强度有一定的提高，结构薄弱部位的承载能力和耗能能力有一定的提高，进而导致结构薄弱层变形的减小。

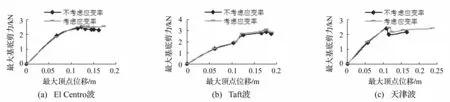
图10 结构x方向的能力曲线

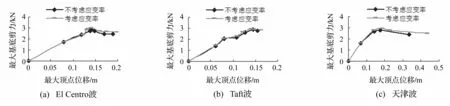
图11 结构y方向的能力曲线

图12 结构在taft波作用下的倒塌过程(不考虑应变率)

图13 结构在taft波作用下的倒塌过程(考虑应变率)

下面以Taft波为例，研究材料的应变率效应对结构倒塌过程的影响。不考虑应变率效应时，结构的倒塌过程如图12所示(峰值加速度调幅到4 m/s2；视图中未显示楼板)。考虑应变率效应后，结构的倒塌过程如图13所示(峰值加速度调幅到4.5 m/s2)。对比图12和图13可以看出，考虑材料的应变率效应后，结构的倒塌过程基本不变，其他两组地震波可得到相同的结论，这里不再给出。考虑到本文模型的特点，可以认为，应变率对简易结构倒塌模式的影响不大。

4 结 论

根据《混凝土结构设计规范》(GB 50010-2010)，开发了ABAQUS显式用户材料子程序VUMAT。采用该程序，研究了材料的应变率效应对结构最大顶点位移、最大基底剪力、最大层间位移、结构的抗倒塌能力和倒塌过程的影响。通过对结果进行分析，得出以下结论：

(1)考虑材料的应变率效应后，如果地震波较弱，结构的最大顶点位移在大多情况下会减小，有时也可能增大。当地震波能使结构接近于发生倒塌时，材料的应变率效应使结构的最大顶点位移明显减小。

(2)考虑材料的应变率后，如果地震波较弱，结构的最大基底剪力在大多情况下会增大，少数情况也可能减小。当地震波能使结构接近于发生倒塌时，材料的应变率效应使结构的最大基底剪力增大。

(3)材料的应变率效应对结构最大层间位移的影响规律与对最大顶点位移的影响规律类似，主要区别在于最大层间位移受应变率的影响更为明显。

(4)当地震波的强度较弱时，受力钢筋不能发生屈服，此时仅有混凝土的应变率效应起作用，应变率对结构响应的影响很小。随着地震波强度的增大，应变率的影响有增大的趋势。

(5)考虑材料的应变率效应后，结构的能力曲线提高，但形状基本不变。

(6)考虑材料的应变率效应后，结构的抗倒塌能力有一定程度的提高，应变率对简易结构倒塌模式的影响不大。

参 考 文 献

[1]林 峰，顾祥林，匡昕昕，等.高应变率下建筑钢筋的本构模型[J].建筑材料学报，2008，11(1)：14-20.

LIN Feng, GU Xiang-lin, KUANG Xin-xin, et al. Constitutive models for reinforcing steel bars under high strain rates[J]. Journal of Building Materials, 2008, 11(1)：14-20.

[2]李 敏，李宏男.建筑钢筋动态试验及本构模型[J].土木工程学报，2008，43(4)：70-75.

LI Min, LI Hong-nan. Dynamic test and constitutive model for reinforcing steel[J]. China Civil Engineering Journal, 2008, 43(4)：70-75.

[3]Bischoff P H, Perry S H. Compressivebehavior of concrete at high strain rates[J]. Materials and Structures, 1991, 24(6)：425-450.

[4]闫东明.混凝土动态力学性能试验与理论研究[D]. 大连：大连理工大学，2006.

[5]董毓利，谢和平，赵 鹏.不同应变率下混凝土受压全过程的实验研究及其本构模型[J]. 水力学报，1997(7)：72-77.

DONG Yu-li, XIE He-ping, ZHAO Peng. Experimental study and constitutive model on concrete under compression with different strain rate[J]. Journal of Hydraulic Engineering, 1997,(7)：72-77.

[6]肖诗云，林 皋，王 哲，等.应变率对混凝土抗拉特性的影响[J]. 大连理工大学学报, 2001, 41(6)：721-725.

XIAO Shi-yun, LIN Gao, WANG Zhe, et al. Effects of strain on dynamic behavior of concrete in tension[J]. Journal of Dalian University of Technology, 2001, 41(6)：721-725.

[7]李 敏. 材料的率相关性对钢筋混凝土结构动力性能的影响[D]. 大连：大连理工大学，2011.

[8]Pankaj P, Lin E. Material modelling in the seismic response analysis for the design of rc framed structures[J]. Engineering Structures, 2005, 27(7)：1014-1023.

[9]GB 50011-2001.建筑抗震设计规范[S].北京：中国建筑工业出版社，2001.

[10]ABAQUS Inc. ABAQUS Analysis User’s Manual[M]. American：ABAQUS INC., 2008.