信赖域-共轭梯度法在麦克斯韦方程参数识别中的应用

王 迎

(黑龙江工业学院 机械工程系，黑龙江 鸡西 158100)

信赖域-共轭梯度法在麦克斯韦方程参数识别中的应用

王 迎

(黑龙江工业学院 机械工程系，黑龙江 鸡西 158100)

针对麦克斯韦方程中的电导率参数识别问题，构造出具有全局收敛性的正则化信赖域共轭梯度算法。此参数识别算法充分融合了最优化领域的传统优化方法—共轭梯度法和新型优化方法—信赖域方法以及正则化方法的优点，使得这种算法具有较强的全局搜索能力，能够很好地应用于麦克斯韦方程的参数识别问题。

麦克斯韦方程；参数识别；正则化；信赖域法；共轭梯度法

0 引言

著名的物理学家、数学家麦克斯韦是在电学和光学方面有很大造诣的科学家，同时也是现代文明的推动者之一。他在总结了相关研究工作的基础上，以数学手法表示出了电磁场理论，演变为后来的麦克斯韦方程组。麦克斯韦方程组实质上是一组偏微分方程，之后一些科学家从这组基本的偏微分方程出发，逐步地发展演变出现代的电子与电力科学技术。麦克斯韦方程的参数识别问题实际上是一个反演问题。随着科学技术日新月异的发展进步，数学物理反演问题的解决方法是近些年来逐步兴起的一类解决几乎遍布于各个科学领域的有效处理问题的方法。它的基本问题是研究各种物理现象的逆过程：首先将物理现象归纳成某种数学模型，然后用它来对物理过程本身或它的载体进行定量分析、过程控制、参数提取或者对实体进行重新设计和改造。随着科学技术的发展和研究范围的扩大，数学物理反问题涉及的也不再仅仅是数学和物理中的反问题，它还涉及到地球物理学、材料科学、图像图形学、模式识别、遥感、石油勘探、工业控制、医学、金融、经济乃至生命科学[1-2]。针对于麦克斯韦方程的反演问题，现今已经产生很多的方法应用于求解这类反问题，然而这些方法下的反演过程是相当复杂的，须要做大量的计算，而且消耗大量的时间。多种情况下，对于这类的反演问题可以利用迭代法(牛顿迭代法)来解决，而利用牛顿迭代法存在的第一个困难就是我们建立的目标函数在局部上会呈现极小化的变化趋势(局部收敛性)。我们需要努力去寻找一种能够有效克服目标函数的局部收敛性并且能够快速检索到所解决的麦克斯韦方程反演问题在其整个定义区间内的最优解(全局最优解)的方法。作为最优化领域的新兴方法之一的信赖域方法是一种全局收敛的数值方法。由此，本文将把信赖域方法引入应用于麦克斯韦方程的参数识别问题中。

本文的总体思路是采用上述方法的有效结合来解决参数识别的问题，具体来说是将全局收敛的信赖域方法与求解大规模优化问题的共轭梯度法有机结合，并引入正则化方法，最终给出了解决麦克斯韦方程中的电导率参数识别问题的全局收敛的数值方法。

1 数学模型的建立

1.1 连续数学模型

二维区域(x，z)∈Ω=[0，l]×[0，h]上的麦克斯韦方程组的电导率参数识别问题模型为：

(1)

(2)

(3)

(4)

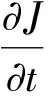
1.2 离散数学模型

对方程(1)～(4)进行差分离散，可以得到如下方程：

i=1,…,m-1,j=1,…,n-1

i=0,…,m

(5)

σT=(σ1,0，σ1,1,…,σ1,n-1,σ2,0,σ2,1,…,σ2,n-1,…σm-1,0,σm-1,1,…,σm-1,n-1),

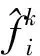
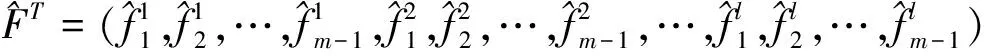
这样反演电导率σi,j的问题便转化为求解如下泛函

(6)

的优化问题。

利用正则化方法在(6)中引入x方向和z方向的二阶光滑矩阵M1和M2，获得用来代替J(σ)的光滑泛函Jα(σ)：

(7)

其中，α为正则化参数。

为了将要求解的二维麦克斯韦方程参数识别问题转化为求解最优化问题，我们求解满足下式的最优解σ*

Jα(σ*)=minJα(σ)

(8)

本文将把(8)式作为参数识别的一般框架，在此框架下讨论麦克斯韦方程反演问题。

Jα(σ)的梯度为

(9)

其中，A′(σ)是A(σ)关于σ的Jacobi矩阵，即

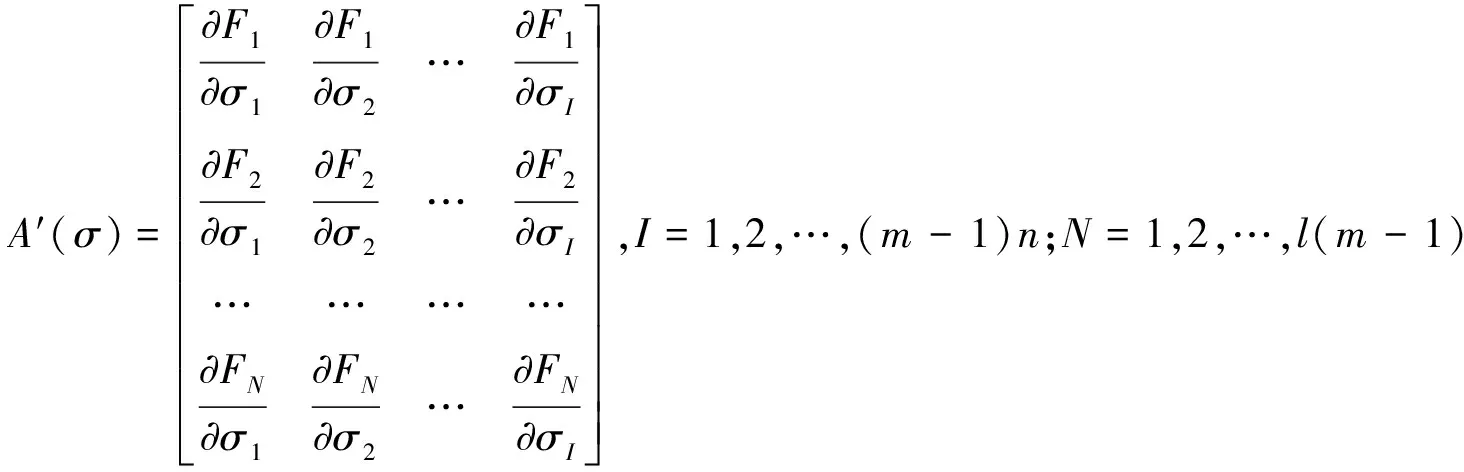
Jα(σ)的海森矩阵为

(10)

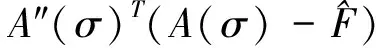
目标函数在某个点σk的二次模型为

(11)

于是，求解(11)的牛顿法为：

(12)

2 全局收敛的参数识别方法的构造

作为最优化领域一种新颖的研究方向，信赖域方法实质上是一种用来求解反问题的正则化方法。假设y为K(x)的二次逼近模型，其基本思想是首先基于如下的最小二乘问题：

其次，在每次迭代的过程中求解下属子问题：

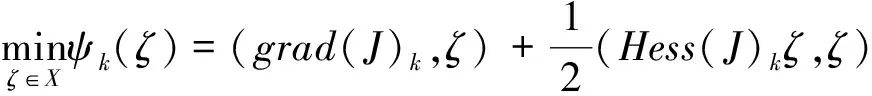
其中，μk为信赖域半径，grad(J)k和Hess(J)k分别表示泛函J在迭代点xk处的梯度和Hessian矩阵：

grad(J)(x)=K′(x)*(K(x)-yδ)，

Hess(J)(x)=K′(x)*K′(x)+K″(x)*(K(x)-yδ)。

多数情况下，Hess(J)(x)含有的二阶项很难精确求得，即使可以求得也计算量巨大[4]。为了有效地克服这个困难，方便地分析问题，我们通常省略Hess(J)(x)的第二项。如果在算法中没有利用海森矩阵中2Jα(σ)中的二阶信息量A″(σ))，则对于大扰动的问题，很可能会导致相应的算法达不到收敛，最终使得求解失败。而在实际问题中，由于)通常难以计算或者或者需要花费巨大的计算量，并且利用整个2Jα(σ)的割线近似又不可取。故而，本文设法构造A″(σ))的割线近似。

(13)

若要求Dk满足拟牛顿条件，则得到Dk+1应该满足的校正公式：

(14)

其中，

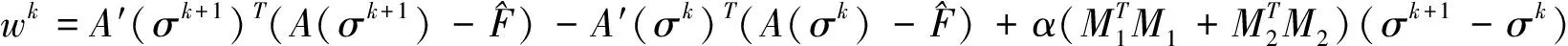
这样做的结果使得海森矩阵更容易趋于对称正定，从理论上更适合于大扰动问题。这是由于随着迭代位置的变化而变过程的进行，构造出的对称矩阵序列{Dk}不断地修正的结果。

2.1 正则化-共轭梯度法

1)给定初始点σ0,D0为对应阶单位矩阵，及给定的精度ε>0，正则化参数α>0,k⟸0。

2)如果k=0，则dk=-Jα(σk)；否则，dk=-Jα(σk)+ξk-1dk-1，其中

3)采用精确线性搜索求步长ηk：

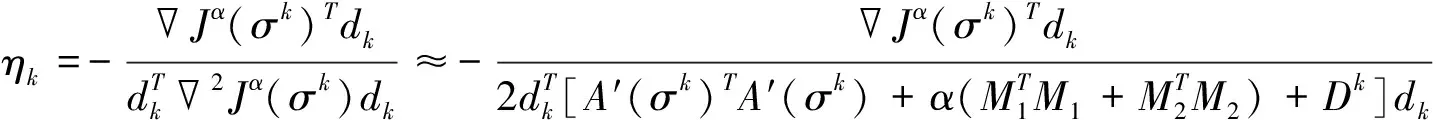
4)令σk+1=σk+ηkdk。

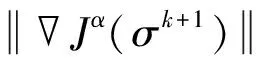
2.2 正则化-信赖域-共轭梯度法

1)令k=0，给出Bk和正则化参数α>0，给定的精度ε>0，D0为对应阶的单位矩阵。

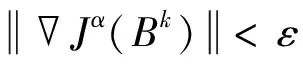
4)如果k=0，则dk=-Jα(Bk)；否则，dk=-Jα(Bk)+ξk-1dk-1，其中

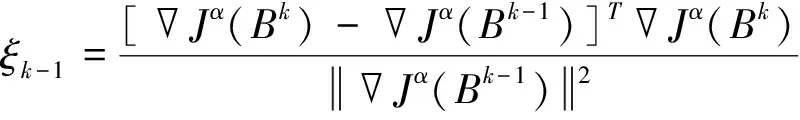
5)采用精确线性搜索求步长ηk：

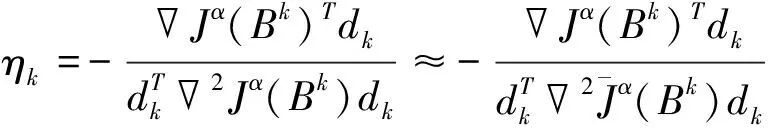
6)令Bk+1=Bk+ηkdk，计算Bk+1。

8)若rkrmax，令α=α/2；否则，保持α不动。

9)若rk≤0，令Bk+1=Bk，Dk+1=Dk；否则，计算Dk+1，k⟸k+1，返回步骤2。

3 结论

由于科学工作者们日趋深入地研究参数识别问题算法的相关知识，已经产生了多种针对参数识别问题的算法，但是截至目前仍未有一种方法能绝对地优于其他方法。从这点上来看，本文进行多种参数识别方法相结合的研究是颇有价值的。为了有效克服麦克斯韦方程反演过程中所固有的困难，本文提出了一种综合共轭梯度法和信赖域法优点的全局收敛的信赖域-共轭梯度算法。该算法不仅有效地解决了局部极小值问题，并且由于该方法本身所具有的一般性，使得它能进一步推广到其他类型的参数识别问题研究之中，因而该方法具有广泛的实用价值和应用潜质。

[1] 韩华,章梓茂,汪越胜.双相介质波动方程孔隙率反演的同伦方法[J].力学学报,2003,35(2):230-238.

[2] H W Engl,A Louis,W Rundell.Inverse problems in geophysical applications[M].SIAM,1997:210-214.

[3] 冯国峰.波动方程反问题的多尺度-信赖域反演方法[D]. 哈尔滨:哈尔滨工业大学,2006:15-17.

[4] 张新明,刘家琦,刘克安.一维双相介质孔隙率的小波多尺度反演[J].物理学报,2008,57(2):593-650.

2014-03-01

王迎(1984-)，女，黑龙江牡丹江人，黑龙江工业学院助教，硕士。研究方向：微分方程数值解。

O224

A

1008-4657(2014)02-0060-05

寸晓非]