反演变换求解二维调和方程的Dirichlet外问题

袁 萍

(长江大学文理学院 基础课部，湖北 荆州 434020)

反演变换求解二维调和方程的Dirichlet外问题

袁 萍

(长江大学文理学院 基础课部，湖北 荆州 434020)

在研究静电场的电位函数、平稳状态下的波动现象和扩散过程时都会遇到调和方程。反演变换又称逆矢径变换，是一种很有效的数学方法。文章首先给出反演变换的定义及性质，然后推导了平面区域上二维调和函数的积分公式，最后利用反演变换将调和方程的Dirichlet外问题化为内问题，得到了二维调和方程圆域外Dirichlet问题的解。

调和方程；反演变换；Dirichlet外问题

0 引言

1 反演点与反演变换

2 二维调和方程Dirichlet内问题的积分表达式

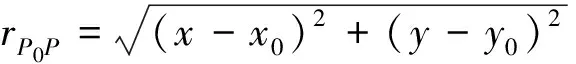
(1)

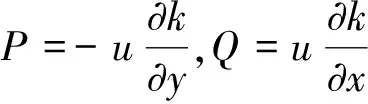
(2)

(3)

(2)与(3)相减得格林第二公式

(4)

由于k(r)在P0处有奇性，需要在D中挖去一个小圆域，以P0为圆心、任意小的ρ为半径做圆域Bρ(P0)。

在区域DBρ(P0)中应用格林第二公式有：

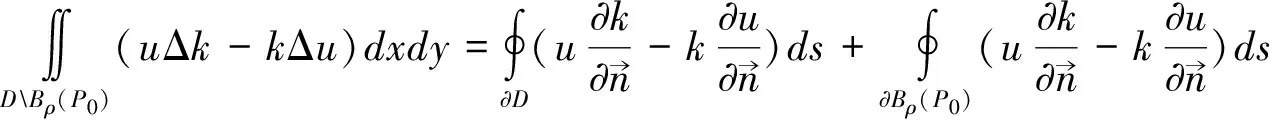
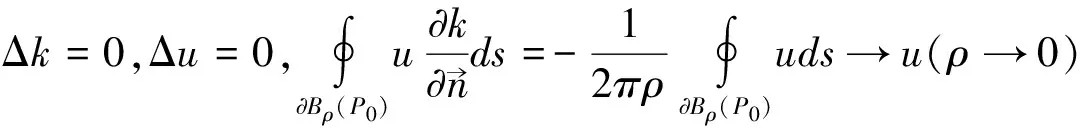
(5)

(6)

(5)与(6)相加得

(7)

记G(r)=k(r)+h(r)，则(7)式为

(8)

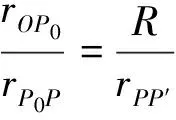
图1 静电源像法求圆域上的格林函数

(9)

3 利用反演变换将圆域Dirichlet外问题化为内问题

设所给Dirichlet外问题为

(10)

利用复合函数求导法则，得

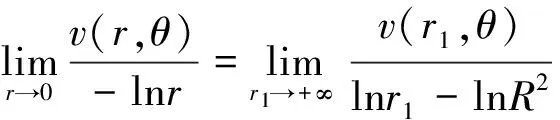
其中(r,θ)为圆域内点的极坐标，(R,φ)为CR(0)上点的极坐标。

[1] 谷超豪.数学物理方程[M].2版.北京:高等教育出版社,2002.

[2] 王明新.偏微分方程基本理论[M].北京:科学出版社,2009.

[3] 于涛.数学物理方程与特殊函数[M].哈尔滨:哈尔滨工程大学出版社,2006.

[4] 刘连璞.平面解析几何方法与研究[M].北京:北京大学出版社,1999.

[5] 倪秀芳,李祥林.复平面上反演变换的性质[J].阜阳师范学院学报:自然科学版,1994(2):42-46.

[6] 陆静.用格林函数法求解二阶微分方程边值问题[J].太原师范学院学报,2011,10(4):32-36.

2014-03-04

袁萍(1984-)，女，湖北潜江人，长江大学文理学院讲师，硕士。研究方向：偏微分方程。

O175.2

A

1008-4657(2014)02-0057-03