Simpson不等式的改进研究
叶宝存
(宁德职业技术学院 福建福安 355000)
Simpson不等式的改进研究
叶宝存
(宁德职业技术学院 福建福安 355000)
Simpson算法是定积分的近似计算方法.在数学问题中,有些定积分是不能牛顿莱布尼茨公式解决的,进而出现了求解近似值即数值解的方法.Simpson不等式就是求解近似值的过程中而产生的不等式.Simpson不等式在数值积分中的作用具有不可替代的地位,很多的数学界先辈对Simpson的误差限优化做出了积极研究和探讨.本文基于Simpson不等式的相关定理,对其最佳误差估计做出论证.
Simpson不等式,分段连续,导数,积分
在数值积分计算中,Simpson公式占有极其重要的地位.Simpson不等式起源一个著名的命题:设函数f(x)在[a,b]区间内,有连续的4阶导数,则有以下结果:
(1)
(2)
其中(2)式就是高等数学领域著名的Simpson公式.
1 Simpson公式中的积分余项定理证明
依据高等数学中取值变量的渐近性质,关于ξ有以下命题:

证明:设定命题的极限为b从右边向左无限趋近于a(按照普遍性数学思维,b>a)情形,根据题设条件将 在区间内的积分表示为含有Peano余项的泰勒公式为:
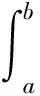


f(4)(ξ)=f(4)(a)+
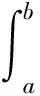

由命题(1)的已知条件,b→a+,ξ∈(a,b),ξ→a+,f(5)(a)≠0因此上式消去近似相等peano余项可得:

(3)


即为:
(4)
由(4)式可以得出,该式的倒数精确度是5次代数精度,而(2)式代数精度为3次.这就构成了Simpson不等式改进的理论基础.
2 Simpson不等式的最佳误差限改进

(5)


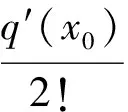
其中ξ∈|x0,x|,则有:
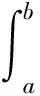
(6)

(7)


(8)

(9)
将(9)式代入(6)式中,可得:
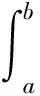

可得出结论为:

(10)
由(10)式,可知改进的Simpson不等式,其收敛阶数大于等于6.
3 结束语
Simpson不等式在数值积分计算中取近似值具有收敛速度快的特性,但Simspon公式在倒数精度较高的计算中会力不从心,本文通过泰勒定理,将Simpson不等式的代数精度提高,扩大了Simpson不等式的应用范围,并提高了公式的收敛阶数,这在复杂函数的高精度计算中具有重大的理论意义.
(责任编辑李平)
2014-5-13
叶宝存, 134860350248@qq.com。
O 172
A
1674-9545(2014)03-0064-(03)

