一般多目标优化问题的凝聚同伦内点算法
贺 莉, 郭 旭, 温延红, 戴嘉轩
(1.长春工业大学 基础科学学院, 吉林 长春 130012;2.长春职业技术学院, 吉林 长春 130033)
一般多目标优化问题的凝聚同伦内点算法
贺 莉1, 郭 旭1, 温延红2, 戴嘉轩1
(1.长春工业大学 基础科学学院, 吉林 长春 130012;2.长春职业技术学院, 吉林 长春 130033)
用凝聚函数把等价转化后的不等式约束条件进行光滑逼近,对目标函数进行线性加权转化成单目标函数,然后利用组合同伦内点方法求解多目标优化问题的最小弱有效解,并证明该方法是整体收敛的。
多目标规划; 凝聚函数; 同伦方法
0 引 言
凝聚同伦内点方法是求解非凸非光滑优化问题行之有效的一种方法。文献[1]给出了求解非凸规划问题的凝聚同伦内点方法;文献[2-5]讨论了可行域在相应条件下约束序列极大极小问题的凝聚同伦内点法;文献[6]研究了改进的凝聚约束同伦方法;文献[7]把凝聚同伦内点方法推广到求解带有不等式约束的凸多目标优化问题,文中在此基础上研究更一般的情形,即同时带有等式和不等式约束的凸多目标优化问题。
考虑下述一般多目标规划(MOP)问题
(1)
其中
文中采用下列记号:
P={1,2,…,p},M={1,2,…,m},L={1,2,…,l};
Ω={x∈Rn|gi(x)≤0,hj(x)=0;i∈M,j∈L}表示可行集;
Ω0={x∈Rn|gi(x)<0,hj(x)=0;i∈M,j∈L}表示严格可行集;
I(x)={i∈{1,2,…,m}|gi(x)=0}表示积极指标集;
∂Ω=ΩΩ0表示可行集边界。
令
易见,不等式约束集合{x∈Rn|gi(x)≤0,i∈M}与{x∈Rn|g(x)≤0}等价。于是问题(1)等价转化为如下单个不等式约束问题:
(2)
定义凝聚函数
t>0
则问题(2)转化为下面的光滑优化问题
(3)
令
文中基本假设:
(C1)f,gi,i∈M为三次连续可微凸函数,hj,j∈L为线性函数;
(C2)Ω0非空有界连通集;
(C3)对∀x∈Ω,向量组(▽gi(x),▽hj(x)|i∈I(x),j∈L)线性无关;

引理1 假设条件(C1)成立,则g(x,θ t)也是三次连续可微凸函数,且g(x)≤g(x,θ t)≤g(x)+θ tlnm。
标注1:由引理1知,当t→0+时,问题(3)的解即为问题(2)的解,从而为问题(1)的解。
引理2

0 引理3 假设条件(C1),(C2)成立,则1)对∀θ∈(0,1],t∈(0,1]有Ωθ(t)⊂Ω; 引理4 假设条件(C1)~(C4)成立,则1)存在θ∈(0,1],使得对∀t∈(0,1],对∀x∈Ωθ(t),向量组(▽xg(x,θ t),▽hj(x)|j∈L)线性无关,即 引理1~引理4的证明可参见文献[3]。 对于问题(3)利用线性加权法将其转化为如下n+p个变量的非线性规划问题 (4) 定义1[8]设x∈Ω,如果不存在y∈Ω,使f(y)≤f(x)(或f(y) 定义2[8]如果(x*,λ*)是问题(4)的最优解,则称x*是问题(3)的最小弱有效解。 (5) 称(x,λ)是问题(4)的K-K-T点,(y,z,ζ,h)是问题(4)的Lagrange乘子。 当t→0+时,方程(5)的K-K-T点收敛于问题(4)的最优解,即为问题(1)的最小弱有效解。 为求解(5)构造同伦方程: (6) 其中 当t=1时,同伦方程(6)变为 (7) 当t→0时,方程(6)的解为方程(5)的K-K-T点,即为问题(1)的最小弱有效解。 证明 用H′(w,w(0),t)记为H的jacobi阵,则 (8) 其中 事实上,由同伦方程(6)中的 下证Γw(0)是有界曲线。若Γw(0)无界,则存在序列{(w(k),tk)}⊂Γw(0),有 由假设(C2)及Λ++的定义及t∈(0,1],存在子列{(w(k),tk)},不妨设其本身,k→+∞,有x(k)→x*∈Ω,λ(k)→λ*∈Λ+,tk→t*∈[0,1],‖(y(k),z(k),ζ(k),h(k)‖→+∞。 下面证明‖(y(k),z(k),ζ(k),h(k))‖→+∞是不可能的。 ‖h(k)‖→+∞,‖ζ(k)‖→+∞的不可能性证明见文献[1]。 1)下面证明若z无界,则‖z(k)‖→+∞(k→∞),由式(6)的第一个方程得 取极限(k→+∞),得 (9) 若式(9)成立,则其极限必存在,记 2)下面证明{y(k)}有界: ﹙Ⅰ﹚当t*=1时,由式(6)的第一个方程有 (10) (Ⅱ)当0≤t*<1时,由式(6)的第一个方程,有 (11) 当取k→+∞的极限时,式(11)左端极限的第一、三、四部分是有限的,而第二部分无穷大,矛盾。所以{y(k)}有界。 由以上讨论知‖w(k)‖→/ +∞,即Γw(0)是有界的。 特别地,如果Γw(0)是有限的,(w*,0)是Γw(0)的另一端点,则w*是K-K-T方程的一个解。 是非奇异的,Γw(0)只能微分同胚于区间(0,1],设(w*,t*)是Γw(0)当t→0+的极限点,则有下列可能情形: 用Γw(0)的弧长s参数化该曲线,即存在连续可微函数w(s),t(s),使得 (12) 微分式(12),得定理4。 定理4 同伦路径Γw(0)由下面的常微分方程初值问题确定 (13) 并且如果有t(s*)=0,则w*=(x(s*),λ(s*),y(s*),z(s*),ζ(s*),h(s*))T是K-K-T方程的解。 多目标优化问题是近30年来迅速发展起来的一门新兴学科,主要研究在某种意义下多个指标同时达到最优的问题。由于所涉及到的多个指标并不是独立的,它们往往是通过决策变量耦合在一起且处于相互竞争、相互冲突的状态,同时所涉及到的函数大多是不光滑的,由此带来的复杂性使得对多目标问题进行优化变得十分困难。文中在已有研究结果的基础上,实现了凝聚同伦内点方法求解一类非光滑凸多目标优化问题的最小弱有效解,扩大了凝聚同伦内点方法的适用范围。 [1] 刘庆怀.解非凸规划问题的组合同伦内点法[D]:[博士学位论文].长春:吉林大学,1999. [2] YU Bo, LIU Guo-xin, FENG Guo-chen, et al. The aggretate homotopy method for constrained sequential max-min problem[J]. Northeast. Math.,2003,19(4):287-290. [3] 金鉴禄,谭佳伟,贺莉,等.一般非线性规划问题的凝聚同伦内点方法[J].吉林大学学报,2011,49(6):1044-1052. [4] 金鉴禄,王秀玉,贺莉,等.约束序列极大极小问题的凝聚同伦内点方法[J].应用数学学报,2010,33(5):792-804. [5] 张春阳,张国霜,李卓识,等.正独立映射的判定及其在非凸优化中的应用[J].长春工业大学学报:自然科学版,2010,31(1):111-114. [6] 苏猛龙,赵立芹,吕显瑞.改进的凝聚约束同伦方法求解一类非线性最优化问题[J].吉林大学学报:理学版,2008,46(6):1094-1096. [7] 杨轶华,赵立芹,吕显瑞,等.多目标凸规划凝聚同伦内点算法[J].吉林大学学报:理学版,2006,44(6):883-887. [8] 林锉云, 董加礼.多目标优化的方法与理论[M].长春:吉林教育出版社,1992. [9] Allgower E L. Numerical continuation methods: an introducation[M]. New York: Springer-Verlag,1990. Aggregate homotopy interior-point method for general multiobjective programming HE Li1, GUO Xu1, WEN Yan-hong2, DAI Jia-xuan1 (1.School of Basic Sciences, Changchun University of Technology, Changchun 130012, China;2.Changchun Vocational Institute of Technology, Changchun 130033, China) Inequality constraint conditions after equivalent transformation is smooth approximated by means of aggregate function, and then the multi-objective function is transferred into a single objective function with linear weighing. We get the minimal weak efficient solution for the multi-objective optimization problem via the aggregate homotopy method, and prove that it is globally convergent. multi-objective optimization; aggregate function; homotopy method. 2014-03-12 国家自然科学基金资助项目(10771020); 吉林省自然科学基金资助项目(20130101061JC) 贺 莉(1970-),女,汉族,吉林图们人,长春工业大学副教授,硕士,主要从事最优化理论与算法研究,E-mail:heli_xu@126.com. O 221 A 1674-1374(2014)06-0601-06

1 主要结果
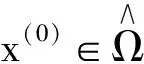










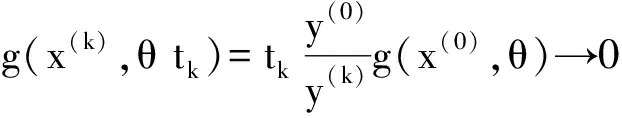
2 算法收敛性




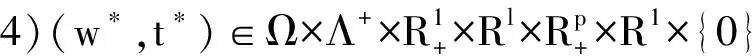

3 结 语

