AunMg(n=1～8)团簇的几何结构和稳定性研究

陈 丽 ,魏成富,3* ,郭建军 , 蒋 斌，金 容

(1.西华大学材料科学与工程学院，四川 成都 610039;2.西华大学物理与化学学院，四川 成都 610039；3.绵阳师范学院，四川 绵阳 621000)

目前虽然对金团簇的掺杂进行了大量研究，但对Au团簇中掺入Mg原子的研究还很少。本文将利用密度泛函理论对AunMg(n=1～8)团簇的几何结构和稳定性进行探讨和研究，用B3LYP/LANL2DZ方法，对其团簇的几何构型进行优化，并通过计算其原子平均结合能、二阶能量差分及HOMO-LUMO能级间隙分布，分析AunMg(n=1～8)团簇的稳定性。

1 计算方法

本文采用密度泛函PW91方法对AunMg团簇的几何结构进行优化，鉴于AunMg(n=1～8)团簇体系电子数多，考虑到原子的性质主要取决于价电子层以及轨道扩展和收缩的相对论效应[10]，对Au和Mg原子分别使用Def2-TZVPP和LanL2DZ基组进行计算。为了找到团簇的基态结构，多重性下进行优化，并用Gaussview软件进行分析，若该结构的频率不为虚频，则此结构被认为是稳定结构，否则该结构是不稳定结构或过渡态。

2 计算结果与讨论

2.1 几何结构

对于AunMg(n=1～8)团簇，本文对其优化后得到许多异构体。对于同一类异构体，图1仅显示了基态结构和与其基态能量最接近的2个异构体，并依次编号为na、nb和nc，给出了异构体的点群、自旋多重性以及相对其基态结构的能量差。

AuMg团簇的结构优化显示，4重态、6重态的能量分别比2重态高1.2eV、1.4eV、故二重态的AuMg为基态结构。Au2Mg的基态结构为线性结构，并且Mg原子处于中间位置。Au3Mg团簇的基态结构为“Y”型结构，与其能量较相近的2个异构体是平面菱形结构，其能量分别比“Y”型结构高0.14 eV、0.87 eV，并且均属于C2V点群。Au4Mg团簇的基态结构4a是一个平面梯形结构，其能量比异构体4b低0.14 eV，异构体4c是出现的第一个三维结构。Au5Mg团簇的基态结构5a是平面结构，由5个金原子半包围着镁原子，异构体5b和5c均为平面结构，其能量明显比基态结构的能量高。随着金原子数的增加，通过几何优化得到的异构体也越来越多；但结果表明，Au6Mg团簇的基态结构仍是平面结构，属CS点群，Mg原子在其中占据最高配位位置，而异构体6b和6c均为三维结构，其能量分别比基态高0.25、0.60 eV。Au7Mg团簇的基态结构是平面结构，属C2V点群，异构体7b和7c均为三维结构。Au8Mg团簇的基态结构是平面“梯形”结构，异构体8b和8c也均为平面结构。通过以上结构分析，我们可以看到AunMg(n=1～8)团簇的基态结构都是平面结构，没有三维的基态结构出现。

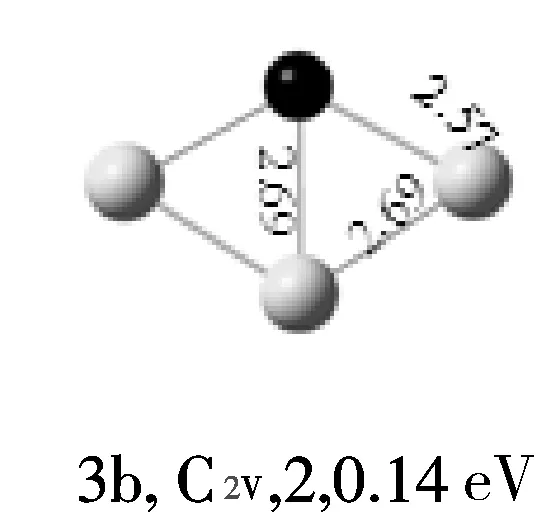
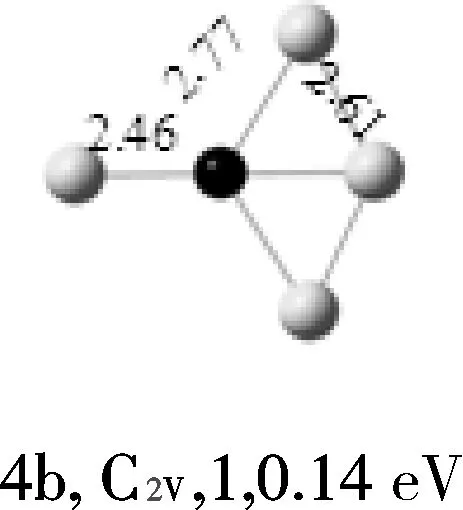
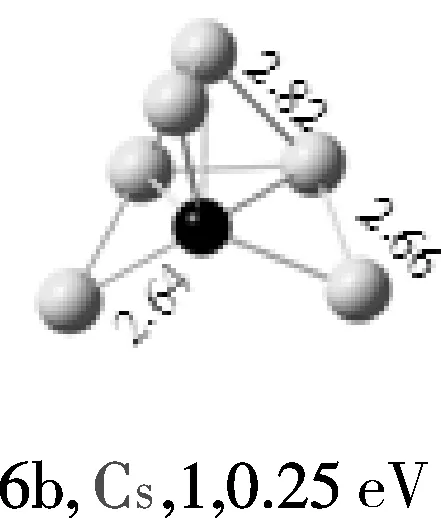
注：键长单位为10-1nm;白色球代表Au原子;黑色球代表Mg原子。

图1 AunMg(n=1～8)团簇的基态结构(第1列)和AunMg的亚稳异构体

2.2 稳定性研究

掺杂团簇的稳定性可通过计算其每原子平均结合能Eb，Eb表征原子核的稳定程度，平均结合能越大，核就越稳定。对于基态的AunMg(n=1～8)团簇，每原子平均结合能的计算公式为：

Eb(AunMg)=[nE(Au)+E(Mg)-E(AunMg)]/(n+1);

(1)

Eb(Aun+1)=[(n+1)E(Au)-E(Aun+1)]/(n+1)。

(2)

式中:E(Au)、E(Aun+1)、E(Mg)、E(AunMg)分别表示金原子、Aun+1团簇、镁原子、AunMg团簇的基态能量。图1给出了AunMg团簇和Aun+1团簇的原子平均结合能随Au原子个数变化的关系。

图2 基态AunMg和Aun+1团簇的每原子平均结合能

从图2中可以看出，AunMg团族的原子平均结合能整体上大于Aun+1团族的原子平均结合能，这表明镁金属原子的掺杂提高了金团族的稳定性。

团簇的稳定性理论上可以利用其能量二阶差分Δ2E值的大小来估计，能量二阶差分值越大，团簇就越稳定，能量二阶差分的计算公式为：

Δ2E[AunMg]=E[Aun+1Mg]+E[Aun-1Mg]-2E[AunMg]

(3)

图3给出了AunMg团簇和Aun+1团簇的能量二阶差分与金原子个数的关系。从图3可看出，随Au原子个数的增加，基态AunMg(n=1～8)团簇的二阶能量差分出现明显的奇-偶振荡性，并且偶数的二阶能量差分高于奇数的二阶能量差分；所以Au原子数为偶数的团簇的稳定性高于含奇数Au原子的团簇，并且n=2时的二阶能量差分最大，即Au2Mg的稳定性最好。

2.3 AunMg(n=1-8)团簇的基态能级分布

由于能级间隙是反映价电子从占据轨道向空轨道跃迁能力的重要参数，在一定程度上反映了团簇参与化学反应的活性，能级间隙越大，化学活性越低。为了进一步研究AunMg(n=1～8)团簇的化学活性，计算了其基态的能级分布，其最高占据轨道(HOMO)、最低空轨道(LUMO)及其能级间隙(HLG)的值如表1所示。

图3 基态AunMg(n=1～8)团簇的二阶能量差分

团 簇HOMO/a.u.LUMO/a.u.HLG/eVAuMg-0.17-0.121.30Au2Mg-0.2200.113.00Au3Mg-0.19-0.170.60Au4Mg-0.20-0.141.74Au5Mg-0.18-0.170.28Au6Mg-0.20-0.151.31Au7Mg-0.19-0.180.24Au8Mg-0.22-0.171.44

能级间隙与金原子个数n的关系如图4所示。

图4 基态AunMg(n=1～8)团簇的HOMO-LUMO间隙

从图4中可以看出，AunMg(n=1～8)团簇的能级间隙出现了明显的奇偶振荡性，并且当n=2、4、6、8时处于波峰，而n=3、5、7时处于波谷，即含Au原子个数为偶数的基态团簇的能级间隙高于含奇数的金原子团簇；故金原子数为奇数的AunMg团簇的化学活性高于偶数的团簇，并且当n=7时的能级间隙最小，n=2时的能级间隙最大，所以Au7Mg参与化学反应的活性最强，Au2Mg的稳定性最好。

3 结 论

本文利用密度泛函PW91方法研究了AunMg(n=1～8)团簇的结构，综合分析得出AunMg(n=1～8)团簇的基态结构，结果表明：AunMg(n=1～8)团簇的基态结构均为平面结构，其中Au2Mg的基态结构为线性结构；Au3Mg团簇的基态结构为“Y”型结构，Au4Mg的基态结构为平面梯形；Au5Mg、Au6Mg的基态结构均为平面多边形；Au7Mg的基态结构是C2V的平面结构；Au8Mg团簇的基态结构是平面“梯形”结构。本文通过计算此基态结构的原子平均结合能、二阶能量差分及HOMO-LUMO能级间隙分布，得出AunMg(n=1～8)团簇的相对稳定性：金原子个数为偶数的团簇的稳定性高于含奇数金原子的团簇，含金原子个数为偶数的AunMg团簇的化学活性低于奇数金原子的团簇；Au2Mg的稳定性最好，但其化学活性较差；Au7Mg的化学活性最强，其稳定性相对较弱。

[1]毛华平，王红艳，倪羽,等. Aun(n=2～9)团簇的几何结构和电子特性[J].物理学报，2004,53(6)：1766-1771.

[2]Bravo Perez G，Garzon I，Novaro O. Non Additive Effects in Small Gold Clusters[J].Chem Phys Lett,1999(313)：655-664.

[3]Tanaka H, Neukermans S, Janssens E, et al. Density Functional Study on Structure and Stability of Bimetallic AuNZn (N≤6) Clusters and Their Cations [J].Chem Phys, 2003, 119(14)： 7115-7123.

[4]Yuan D W, Wang Y, Zeng Z. Geometric, Electronic, and Bonding Properties of AuNM (N=1 ～7, M=Ni, Pd, Pt) Clusters [J]. Chem Phys, 2005, 122(11)： 114310.

[5]王红艳，李喜波，唐永健,等.AunXm(n+m=4,X=Cu,Al,Y)混合小团簇的结构和稳定性研究[J].物理学报,2005,54(8)：3565-3570.

[6]毛华平，王红艳，朱正和,等.AunY(n=1-9)掺杂团簇的结构和电子性质研究[J].物理学报，2006，55(9)：4542-4547.

[7]迭东，邝小渝.Co@Aun(n=1-8)团簇的几何结构和电子性质的理论研究[J].原子与分子物理学报，2012，29(2)：267-272.

[8]Janssens E，Tanaka H, Neukermans S, et al. Electron Delocalization in AuNXM(X=Sc,Ti,Cr,Fe) clusters： A Density Functional Theory and Photofragmentation Study[J]. Phys Rev B, 2004, 69(8)： 085402.

[9]葛桂贤，闫红霞，井群,等.Density Functional Theory Study on the Structure and Electronic Properties of AunSc(n=1-7) Clusters[J].物理学报，2011，60:033101.

[10]Andrae D, Häuβermann U, Dolg M, et al. Energy-adjusted ab Initio Pseudo Potentials for the Second and Tthird Row Transition Elements [J]. Theor Chim Acta, 1990, 77： 123-141.