基于改进遗传算法的区域交通信号优化控制
刘脐锺,李 兵
(西华大学数学与计算机学院,四川 成都 610039)
区域交通信号控制策略优化属于全局优化问题,而遗传算法对于解决这种多变量全局最优解的问题具有明显优势;因此,近年来对区域交通信号控制策略进行优化的研究大多采用了遗传算法或其改进算法。目前对遗传算法改进的研究大部分是针对交叉和变异概率[1-3]进行的,其交叉和变异的操作单位为个体。HCM2000[4]模型中的车辆延误计算模型被大量采用,但是该模型没有考虑相位差因素。本文首先将区域交通流分为中间交通流和边界交通流,将相位差因素考虑在内,使区域内的所有交叉口相互关联,并且与HCM2000中的车辆延误模型结合,建立以车辆平均时延最小化为目标的延误模型;然后,再进一步改进遗传算法,将参数的约束条件融入编码过程,使在求解过程中就能达到约束参数的目的,同时将个体中各个参数分割开来,对各个参数分别执行交叉和变异操作,以提高求解中各参数的多样性;最后,根据改进的遗传算法对延误模型求最优解,实现对区域交通信号控制的全局优化。
1 区域交通信号优化控制模型
以最小化区域车辆的平均延误为目标,模型的建立是一个递进的过程。如图1所示,箭头表示包含关系,以单路口的某条交通流的1辆车的延误为基本运算单位,以整个区域在一段时间内的车辆数为运算总量,以此来建立目标函数。涉及的参数有路口周期、相位时间、相邻路口的相对相位差、车流量、车速、相邻路口之间的距离等。主要考虑的约束重点是路口周期、相位时间和相位差,约束条件如1.1所述,目标函数的建立过程如1.2所述。

图1 模型中的包含关系
1.1 优化参数及约束条件
该模型中主要优化的参数是各路口的周期时间Ci,各路口的相位差时间PDi以及各路口的相位时间Pi。每个交叉路口的最大周期Ci,max和最小周期Ci,min是常量,但是每个交叉口的周期Ci必须符合约束条件
Ci,max>Ci>Ci,mini∈N。
(1)
式中N是区域中交叉路口的集合。为使各个路口的相位差和相位时间能够进行统一优化,在同一区域内各个路口的周期时间为相同值,即Ci=Cj。
在交通控制中,需要提供最小绿灯时间用来保证交通安全。根据HCM2000,最小绿灯时间GMIN的定义为:
GMIN=3.2+L/Sp+0.824×(Np/W)W>3;
(2)
GMIN=3.2+L/Sp+0.27×NpW≤3。
(3)
式中:L代表人行横道的长度;Sp代表行人的平均速度;W代表人行横道的宽度;Np是一个周期内的行人数量。相位时间必须大于或等于最小绿灯时间,即符合
GREENi,j≥GMINi,ji∈N,j∈Pi。
(4)
式中Pi是交叉口i的相位集合。
2个相邻路口,协调相位的开始时间之差称为相位差。相位差的约束需要考虑到协调相位的上行和下行,比如,协调相位是一个直行相位,那么可以将1个交叉口的上行定义为从交叉口i到交叉口j,下行定义为从交叉口j到交叉口i,如图2所示。
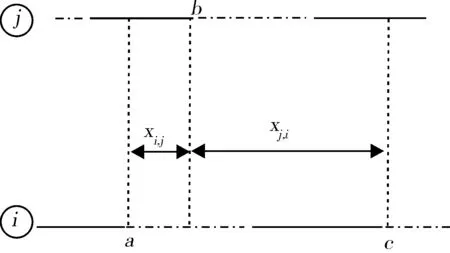
图2 相位差示意图
图中对应于i,j的2条横线分别表示交叉口i和j的相位时间,其中实线表示红灯的时长,虚线表示绿灯的时长,从i到j方向的绿灯从a点开始。由于上行相位差, 所以从j到下一相邻路口方向的绿灯从b点开始。又由于下行相位差,所以从i到j的交通流通行绿灯从c开始。Xi,j是上行相位差,Xj,i是下行相位差。在协调相位的方向上,上行和下行的相位差必须满足相位闭合条件也就是符合约束:
Ci≥Xi,j≥0i,j∈N;
(5)
Xi,j+Xj,i=n·Ci。
(6)
其中n为整数,图1就是n为1时的相位差情况,即2个路口正好是相邻路口的情况。
1.2 目标函数的确立
区域交通信号优化的主要目标是通过优化决策变量使整个区域内车辆的平均延迟时间最小化。目标函数表达式为
(7)
式中:Fi,j,k是交叉口i第j相位第k个交通流的流量;Di,j,k是第i交叉口第j相位第k个可放行交通流的平均延误时间。
根据车流饱和度的不同,HCM2000中的延误模型采用不同的计算公式,可以计算出饱和状态和非饱和状态下的车辆延误。该模型考虑了车流离散和上游交叉口控制等因素,但没有考虑相位差因素;然而相位差对于相邻交叉口起到协调相位的作用,所以将相位差融入延误模型中,可以进一步提高交通信号的控制效果。
将交通流分为2种类型:一种是入口交通流,也就是区域中的边界交通流,不需要考虑相位差;另一种是中间交通流,也就是需要考虑相位差的交通流。对于入口交通流的延误,使用HCM2000提供的公式,其表达式为:
(8)
(9)
式中:GREEN为相位绿灯时间;x为通行饱和度;d3为存在初始队列而增加的延误;T是交通状况的持续时间;K是车辆离开路口所服从的分布;I为车辆到达路口所服从的分布。
对于中间交通流,要考虑到相位差,假设2个交叉口A、B之间的路段长度为L,平均车速为V,R是一个周期内从A到B的交通流的红灯时间,PA,B是交通流从A到B时交叉口B的下行相位差,S为交叉口B的最大通行能力,Q为交通流量,则当(L/V)modC (10) 其中mod是取余运算。当(L/V)modC≥PA,B时,从A到B的交通流的延误为 (11) 这里将交通参数的约束条件融入遗传算法的编码中,并且在改进遗传算法的基础上对交叉和变异过程进行再次改进,并对上述建立的模型求最优解。 在遗传算法中,编码必须保证决策变量的范围与遗传空间中染色体对应基因的范围对应,决策变量的位数可按以下规则决定。 设决策变量的范围为1到X,若n满足2n-1 (12) 以1个交叉口为例,将交叉口分为主道路和次道路,如图3所示。设图中1、2、5、6交通流为主交通流,3、4、7、8交通流为次交通流,1和5所示方向可设为一个相位,2和6,3和7,4和8所示方向各设为一个相位,ti表示交通流i的绿灯时间,tm表示一个周期内主交通流绿灯总时间,tc表示一个周期内次交通流绿灯时间,tg是一个周期中的相位切换时间,则tm=t1+t2=t5+t6,tc=t3+t4=t7+t8。采用5个决策变量{f1,f2,f3,f4,f5},各决策变量的有效位数分别为6、6、5、5、6。f1对应周期长度,f2对应于主交通流绿时,f3,f4分别对应于t1、t3,f5对应相位差。根据公式(12),解码后周期C=Cmin+(Cmax-Cmin)×f1/63。主交通流的最小绿灯时间tmmin=MIN{t1min+t2min,t5min+t6min},次交通流的最小绿灯时间tcmin=MIN{t3min+t4min,t7min+ t8min}。根据式(12)可以求出tm=tmmin+(tmmax-tmmin)×f2/31,剩余的变量可以采用类似的方法来进行解码。 图3 交叉口交通流流示意图 遗传算子的操作是遗传算法的核心,算法的性能和效果很大程度上受遗传算子的影响[5-6]。一般的遗传算法中,交叉算子的交叉概率和变异算子的变异概率是固定的,这种方式有利于减小算法的计算负荷;但是随着遗传代数的增加,有可能会淘汰一些优良的个体,容易陷入局部收敛[6-8],从而失去全局优化的效果。目前一些对遗传算法的研究对交叉和变异概率进行了改进,本文采用了这些改进。 第n代的交叉概率为: (13) (14) 第n代变异概率为: (15) PMUn=PMUmaxF≤Fav。 (16) 式中:PCRmax是最大交叉概率,GN是遗传总代数,Fm是第n-1代群体中个体的最大适应度,F是2个交叉个体的最大适应度,Fav是平均适应度。PMUmax是最大变异概率。 另外,以往的研究都是以个体为单位来进行交叉和变异操作,这样不利于提高求解过程中各参数的多样性。本文将个体中各个参数分割开来,对各个参数分别执行交叉和变异操作。比如一个个体的编码为{f1,f2,f3,f4,f5},那么交叉和变异过程如图4和图5所示,即个体1中的f1与个体2中的f1进行交叉和变异,个体1中的f2和个体2中的f2进行交叉和变异,以此类推。 图4 交叉操作示意图 图5 变异操作示意图 本文的目标函数DELAY是一个求最小值的问题,用遗传算法求解,需要将其转化为求最大值的问题,即将目标函数转化为算法中的适应度函数 (17) 用以上的改进遗传算法对模型求最优解,实现交通区域信号的优化控制,其过程如下:1)获取交通基本参数信息,如最大周期时间、当前各个路口的车流量、参与计算的交叉路口数等;2)初始化遗传算法中的参数,如最大最小交叉概率、变异概率以及种群规模和遗传代数等;3)随机生成初始群体;4)计算个体的适应度的值;5)根据适应度进行选择操作;6)根据交叉概率进行交叉操作;7)根据变异概率进行变异操作;8)判断是否达到终止条件,如果没有则继续下一步,如果达到终止条件,则跳转到第11)步;9)判断是否达到最大遗传代数,如果没有达到,则转到第4)步继续执行,如果达到最大遗传代数,则进行下一步;10)将每一代中所保存的最优个体和最终的最优个体联合比较,选出适应度最大的个体;11)将最终的最优个体的参数解码后输出。 VISSIM是一种微观、基于时间间隔和驾驶行为的仿真建模工具[9-10],用以建模和分析各种交通条件下(车道设置、交通构成、交通信号、公交站点等)城市交通和公共交通的运行状况,是评价交通工程设计和城市规划方案的有效工具。这里对2种方案进行仿真。 方案1:采用HCM2000中提出的时延模型,并且使用对交叉遗传概率改进后的遗传算法[11]。 方案2:在方案1的基础上融入相位差因素,并且将个体中各个参数分割开来,对各个参数分别执行交叉和变异操作。 以一个4交叉路口所组成的区域为例进行仿真,如图6所示。4个交叉口编号分别为a,b,c,d,边界路口分别为①、②、③、…、⑧,从边界路口进入的交通流大小如表1所示,每条路段有2个车道:一个为左转专用车道,另一个为直行和右转共同使用车道。相位序列采用如图7所示。 图6 4交叉路口区域 图7 相位序列 边界路口→交叉口交通流量/(辆/h)①→a900⑦→a500②→b800③→b300⑤→c1 110⑧→c600④→d1 000⑥→d1 000 表2 2种方案下的优化结果 从表2中可以看出,方案2得出的周期要大于方案1的周期,这就使得在周期不超过自身约束的情况下,各个相位能够分配的时间更多。将表2中2种方案的数据作为输入参数,利用VISSIM对上一小节提出的交通情况进行仿真,得出的结果如表3所示,优化后整个区域的平均车辆延误比优化前减少了7.3 %。其中每个路口的车辆延时情况如图8所示。从表3和图8中可以看出,在方案2控制下,第3个交叉口的延误虽然要高于在方案1控制下该路口的延误,但是整个区域的平均延误却降低了。 表3 仿真结果 图8 2种方案控制下各交叉口延误 本文以区域为单位对交通信号控制进行优化,在建立模型的过程中将HCM2000中提到的延误计算方法与添加了相位差因素的延误计算方法相结合,采用改进后的遗传算法进行全局优化。从仿真结果可以看出,本文提出的方案可能会使个别交叉口的车辆延误大于改进前方案的车辆延误,但从整个区域的角度来看,该案却能取得更好的效果,达到了对区域交通信号进行全局优化的目的。 [1]雷胜.城市交通流量智能组合预测方法研究[J].西华大学学报:自然科学版,2006:25(2):60-63. [2] 陈小锋,史忠科.城市交通干线信号动态优化控制方法[J].西北工业大学学报:自然科学版,2010,28(4):579-584. [3]金晶,苏勇.一种改进的自适应遗传算法[J].计算机工程与应用:计算机科学,2005,18(4):64-69. [4]庄宏斌,周亚平,曹宪生.基于改进遗传算法的区域交通信号配时优化[J].交通运输系统工程与信息:交通工程,2012,12(4):57-63. [5] 刘智勇.智能交通控制理论及应用[M].北京:科学出版社,2003:20-50. [6]李敏强.遗传算法的基本理论与应用[M].北京:科学出版社,2006:1-45. [7] Jiao Jian,Lin Jun,Lin Dongshu.Research to Improve the Optimization Speed of the Genetic Algorithm[J].Advances in Information Sciences and Service Sciences,2011,3(10):461-468. [8]吴恩,杨晓光,吴震,等.基于遗传算法的干线协调控制参数共同优化[J].同济大学学报:自然科学版,2008,36(7):922-926. [9]易江涛,张亚杰.VISSIM和Synchros在相邻交叉口优化中的应用[J].公路与汽运:城市交通,2013,4(4):76-80. [10] 胡明伟,郭秀芝.用微观交通仿真软件实现ITS模拟的比较研究[J].交通与计算机:计算机应用,2004,22(4):19-22. [11]葬利林.城市交通信号优化控制算法研究[D].济南:山东大学,2007.2 遗传算法的改进
2.1 染色体编解码方法

2.2 遗传算子的确定
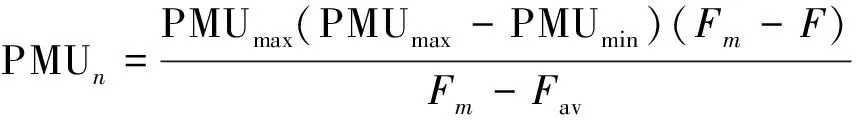

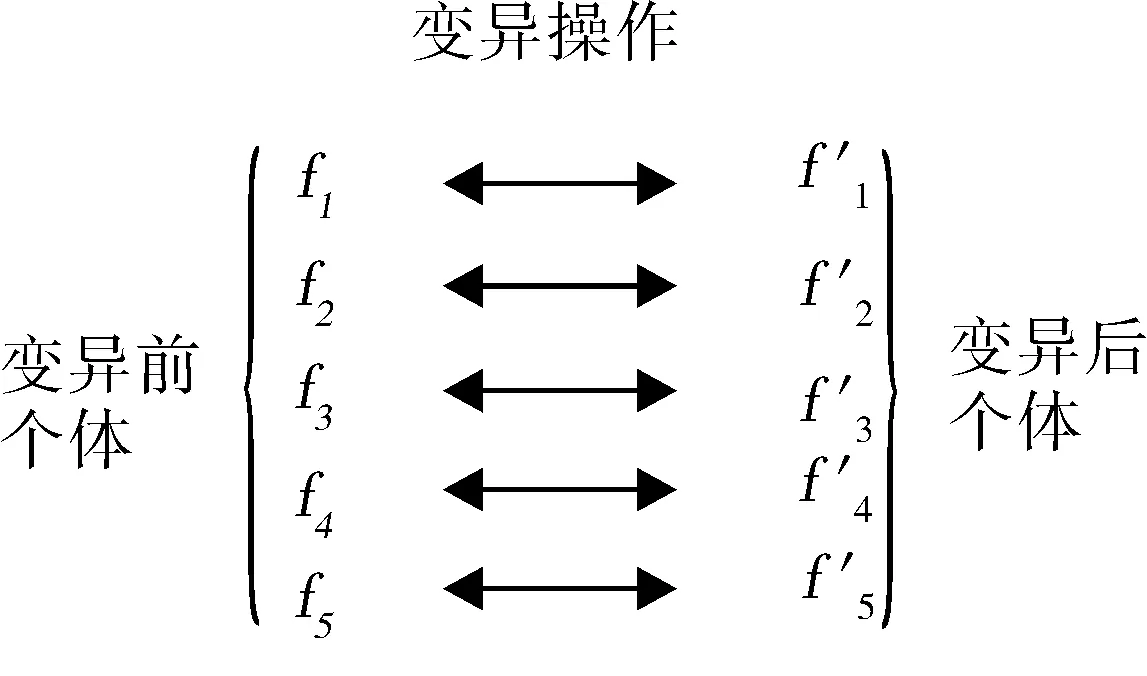
2.3 适应度函数的确立
2.4 交通区域信号控制优化流程
3 区域交通信号仿真实验
3.1 仿真数据及道路设置




3.2 仿真结果


4 结束语

