基于推力磁链的永磁直线同步电机自适应观测器

王兴贵，王宏雨

（兰州理工大学 甘肃 兰州 730050）

基于推力磁链的永磁直线同步电机自适应观测器

王兴贵，王宏雨

（兰州理工大学 甘肃 兰州 730050）

永磁直线同步电机由于结构的特殊性使其直交轴电感不相等，数学模型变得较为复杂，传统的观测器不再适用于直线电机。同时直接推力控制依赖观测器观测结果的准确性，尤其在低速阶段，以线性模型为基础建立的观测器不能很好地适应电机参数变化。根据永磁直线同步电机的数学模型，采用了推力磁链等效的方法，简化了其数学模型，从而解决了交直轴电感不相等引起的推力观测误差。同时，在自适应观测器中引入定子电阻自适应律，减小了低速段由于电机参数变化引起的定子磁链观测误差，提高了直接推力控制的低速段性能。并建立了相关的仿真模型，对定子磁链和电磁推力的观测效果进行了分析，从而验证了基于推力磁链的自适应观测器的有效性。

永磁直线同步电机；自适应观测器；直接推力控制；推力磁链

永磁直线同步电机（permanent magnet linear synchronous motor PMLSM）具有推力强度高、时间常数小、响应快等优点。结合直接推力控制（direct torque control DTC）制理论可获得较高的控制精度，在精密仪器中应用广泛[1]。但由于PMLSM参数摄动、边端效应等不确定因素，若要获得PMLSM DTC系统高性能的推力动态控制性能及更加平稳的低速运行性能，定子磁链和电磁推力观测的准确性至关重要[2-3]。

由于电磁推力的观测是以定子磁链为基础，所以定子磁链的准确观测意义重大，对于定子磁链的观测，最基本的方法有电压模型法和电流模型法[4-5]。无论电压模型还是电流模型，本质上为开环观测器，受电机参数变化及模拟量采样误差影响较大，很难适应直线电机对于定子磁链观测精度的要求[6-7]。在旋转嵌入式永磁电机中采用有效磁链等效的方法可以消除电机电感参数的影响，实现其数学模型与经典模型的统一[8]。本文中在PMLSM中采用推力磁链等效的方法，研究了一种新的定子磁链自适应观测器，旨在消除PMLSM模型中电感对定子磁链观测的影响，提高直接推力控制中低速段定子磁链和电磁推力的观测精度，提高系统的控制性能。

1 推力磁链自适应观测器设计

1.1 PMLSM基于推力磁链的数学模型

参考旋转电机模型，αβ为静止坐标系；dq为动子同步坐标系。由于其结构的不完全对称造成dq轴电感不相等，PMLSM的数学模型会有所不同[1]。dq坐标系中电磁推力方程为：

可以引入推力磁链（有效磁链）：

电压方程由推力磁链表示为：

利用坐标变换将式（3）和（4）变到α β静止坐标系中为：

其中，ψs为定子磁链，ψf为永磁磁链，LdLq为dq轴电感，Rs为电子电阻，Ve为电磁线速度，τs为极距，ρn为极对数，ρ为微分因子。若能在αβ坐标系中观测出推力磁链ψeα和ψeβ，由此可以直接计算出电磁推力，根据式（8）观测出定子磁链。

1.2 自适应观测器设计

电机中电气常数远小于机械常数，推力磁链公式（6）经微分可以得到其状态方程为：

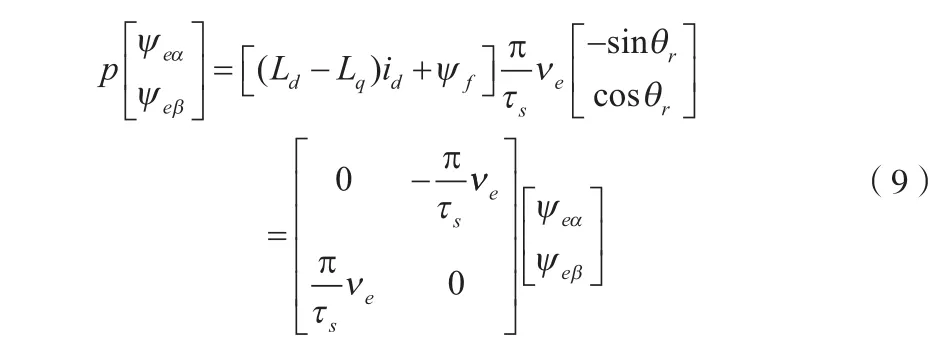
由式（5）和（9）可得PMLSM的状态方程为：

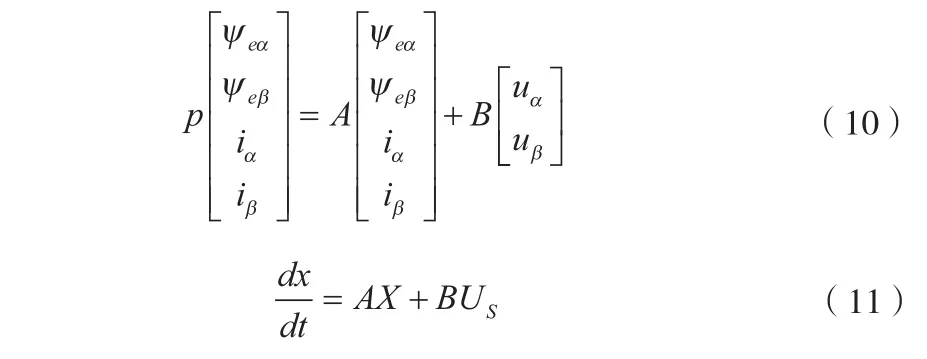
基于推力磁链利用状态方程可以构建如下自适应状态观测器：

观测器状态■d矩xˆ 阵= Aˆ xˆ是 +定 Bπuν子 +电 K阻的i函）数■，K为增益矩阵，■■dt0τL S

e −L s 0■■自适应状态观测■器利用观测s与q 实际电q流误差■来调节自适应机构，在自适应律■的−π作ν用e 下，0能不断0修正−定Rˆs子 ■电阻参数，使观测模型更接近实■■际τ模L型，减小定子磁链观L测■■误差。

sq q

将式（11）与（12）相减得到误差e的状态方程：

其中，Kρ＞0，Ki＞0。由式（12）、（16）可以构建自适应观测器，观测出推力磁链后通过式（8）可以计算出定子磁链，同时可以直接观测出电磁推力。

2 基于推力磁链自适应观测器PMLSM DTC系统仿真分析

2.1 PMLSM DTC系统结构框图

基于Matlab/Simulink构建推力磁链自适应观测PMLSM DTC系统，结构如图1所示。外环采用速度闭环，速度调节器输出为电磁推力给定 ，内环为推力闭环，自适应观测器输出电磁推力与其给定比较得到定子磁链偏差角Δδsm，经过预测电压矢量计算得到给定电压的幅值和角度，实现速度和电磁推力的双闭环控制。

PMLSM参数：UN=220 V；M=20 kg；τS=0.036 m；nρ=2；Rs=2.3 Ω；Ld=11.65 mH；Lq=18.75 mH；ψf=0.45 Wb；同步速度vs=3.6 m/s。定子磁链给定为0.8 Wb，直线电机初始负载为30 N。在仿真中将不同模型观测器得到的定子磁链进行对比，检验基于推力磁链自适应观测器的观测效果。

图1 PMLSM DTC系统结构图Fig.1 PMLSM DTC system structure

2.2 观测器稳态性能

分别采用推力磁链自适应观测器和电压模型观测器对定子磁链进行观测，以电流模型定子磁链观测器输出为基准，在高速和低速时，比较不同模型对定子磁链的观测误差，如图2～图5所示。

图2 1 m/s时电压模型观测器磁链波形Fig.2 Voltage model observer flux waveforms 1 m /s

图3 1 m/s时基于推力磁链自适应观测器磁链波形Fig.3 Thrust flux adaptive observer flux waveforms 1 m /s

由图2和3可知，高速1m/s时推力磁链自适应观测器定子磁链观测值的误差最大为0.09 Wb，电压模型误差最大为0.2 Wb，都与电流模型的观测波形基本重合。

由图4和5可知，低速0.05 m/s时推力磁链自适应观测器的误差最大为0.1 Wb，电压模型误差最大为0.4 Wb。由此可见，在高速时两种模型观测器的观测精度相差并不大，在低速时由于直线电机参数的变化，电压模型观测器的误差会加大，同时磁链波形会发生畸变和相位偏移，但对推力磁链自适应观测器的影响并不明显。

图4 0.05 m/s时电压模型观测器磁链波形Fig.4 Voltage model observer flux waveforms 0.05 m /s

图5 0.05 m/s时推力磁链自适应观测器磁链波形Fig.5 Thrust flux adaptive observer flux waveforms 0.05 m /s

在低速0.05 m/s、初始负载30 N、0.5 s时突增为50 N时，不同模型电磁推力观测波形如图6所示。

图6 0.05 m/s不同模型观测器电磁推力波形Fig.6 Different models observer thrust waveforms 0.05 m /s

由图6不难看出在低速时，磁链的观测误差必会引起电磁推力观测误差，其中推力磁链自适应观测器对电磁推力的观测波动更小，从侧面也可以看出采用自适应观测器的系统对推力控制更加准确。

2.3 观测器鲁棒性

PMLSM 1 m/s运行时，定子电阻变量为±0.5Rs，可以检验推力磁链自适应观测器对模型参数变化的鲁棒性。不同定子电阻时推力磁链自适应观测器定子磁链如图7所示。

图7 1.5 Rs时基于推力磁链自适应观测器磁链波形Fig.7 Thrust flux adaptive observer thrust waveforms 1.5 Rs

由图7中可知，1.5Rs时自适应观测器的定子磁链观测值与原观测值基本重合，之间误差为0.05 Wb，0.5Rs时误差基本相同，磁链前期的非正弦是由启动造成。从中可以看出推力磁链自适应观测器引入定子电阻自适应律，对定子电阻变化的鲁棒性变好，可以改善基于PMLSM线性模型建立的观测器性能。

2.4 PMLSM DTC系统性能分析

采用推力磁链自适应观测器PMLSM DTC系统的初始速度给定为0.05 m/s，0.02 s时突增至1 m/s，初始负载推力为50 N，0.5 s时增至100 N，速度阶跃和推力阶跃响应如图8所示。

图8 PMLSM DTC系统阶跃响应波形图Fig.8 PMLSM DTC step response waveforms

由图8可知，采用推力磁链自适应观测器的PMLSM DTC系统电磁推力波动小，响应较快，速度控制精度高，尤其是低速也能运行稳定。

3 结 论

文中针对PMLSM特殊结构引起数学模型复杂的问题，基于其电磁推力公式采用推力磁链等效直轴磁链的方式，简化了其数学模型，从而解决了交直轴电感不相等对定子磁链和电磁推力观测带来的困难，观测器的模型不再受直轴电感的影响，提高了观测的精度。

与此同时，在观测器中引入定子电阻自适应律，减小了低速段由于定子电阻参数变化引起的定子磁链观测误差，增强了观测器的鲁棒性，从而提高了PMLSM DTC系统的低速性能。

[1] 王成元，夏加宽，杨俊友，等.电机现代控制技术[M].北京：机械工业出版社，2008.

[2] 余佩琼，陆亿红，王涌，等.永磁直线同步电动机无位置传感器控制系统的研究[J].中国电机工程学报，2007，27（24）：53-57.

YU Pei-qiong，LU Yi-hong，WANG Yong et al.Research on permanent magnet linear synchronous motor position sensorless control system[J].Proceedings of the CSEE，2007，27（24）：53-57.

[3] 刘成颖，王昊.基于非线性电感分析的永磁直线同步电机电磁推力特性研究[J].中国电机工程学报，2011，31（30）：73-75.

LIU Chengying，WANG Hao.Research on thrust characteristics in permanent magnet linear synchronous motor based on analysis of nonlinear inductance[J].Proceedings of the CSEE，2011，31（30）：37-75.

[4] 贾洪平，贺益康.一种适合 DTC 应用的非线性正交反馈补偿磁链观测器[J].中国电机工程学报，2006，26（1）：101-105.

Jia Hongping，He Yikang.A new nonlinear perpendicular flux observer with compensation feedback suitable for DTC application [J].Proceedings of the CSEE，2006，26（1）：101-105.

[5] 周扬忠，钟技.用于永磁同步电动机直接转矩控制系统的新型定子磁链滑模观测器[J].中国电机工程学报，2010，30（18）：97-102.

Zhou Yangzhong，Zhong Ji.A novel stator flux linkage estimator based on sliding mode theory for direct torque control of permanent magnet synchronous motor[J].Proceedings of the CSEE，2010，30（18）：97-102.

[6] Hasegawa M，Matsui K.Position sensorless control for interior permanent magnet synchronous motor using adaptive flux observer with inductance identification[J].IET Electric Power Applications，2009，3（3）：209-217.

[7] B.Sheikh-Ghalavand，S.Vaez-Zadeh，A.Hassanpour Isfahani.An mproved Magnetic Equivalent Circuit Model for Iron-Core Linear Permanent-Magnet Synchronous Motors[J].IEEE transactions on magnetices，2010，4（1）：112-119.

[8] Paicu M C，Boldea I，Andreescu G D，et al.Very low speed performance of active flux based sensorless control：interior permanent magnet synchronous motor vector control versus direct torque and flux control[J].IETElectric Power Applications，2009，3（6）：551-561.

A adaptive observer based on thrust fl ux principle for permanent magnet linear synchronous motors

WANG Xing-gui，WANG Hong-yu
（Lanzhou University of Technology，Lanzhou 730050，China ）

The special structure of permanent magnet linear synchronous motor cause direct and cross axis inductance deviation，the mathematical model becomes more complex，the traditional observer is no longer applicable to linear motors.And the direct thrust control is dependent on the accuracy of observations，observer based on linear mode isn't well adapted to the change of motor parameters especially in the low stage.According to the mathematical model of linear motor，the thrust flux is introduced，which simplifies the mathematical model and solves the thrust observation error caused by the deviation between direct and cross axis inductances.Adaptive law of stator resistance is introduced into the adaptive observer，which reduces the error of stator flux observation due to the motor parameter changes and improves the control performance of direct thrust control at low stage.And the simulation model is established，the effectiveness of adaptive observer based on thrust flux is verified through the analysis research stator flux and thrust observations.

permanent magnet linear synchronous motor（PMLSM）；adaptive observer；direct torque control（DTC）；thrust flux

TN06

A

1674-6236（2014）11-0071-04

2014-03-17 稿件编号：201403176

甘肃省科技支撑计划（1204GKCA003）

王兴贵（1963—），男，甘肃天水人，教授。研究方向：可再生能源发电系统与控制，微电网技术，电力电子与电力传动。