简谐激励下一类干摩擦振子的响应计算

王本利，张相盟，刘 源，马 平

（1.哈尔滨工业大学 卫星技术研究所，150080哈尔滨；2.中国人民解放军91216部队，125106辽宁兴城）

装配结构中，大量存在着各种机械连接，诸如螺接、铆接、法兰式连接或其他紧固式连接，这些连接也被称为“硬连接”［1］.实际上，此类连接并不完全紧固，当外激励量级较大时，其连接接触面常会产生微滑移（Microslip）甚至宏滑移（Macroslip），与之伴随的干摩擦是结构阻尼的一个重要来源，这种干摩擦阻尼甚至可占到整个结构阻尼的90%［2］.由于这种连接还会改变连接处的局部刚度，从而会影响整个结构的动力学特性及动态响应［3］.因此，在进行整体装配结构计算时，需要对连接处特别考虑.

库伦模型是一种简单常用的摩擦模型，它已被广泛应用于描述摩擦阻尼或摩擦连接处的建模和计算中.这方面的工作可以追溯到Den Hartog［4］，他首次计算了同时含有库伦阻尼器和粘性阻尼器的振子系统的稳态响应.Lee等［5］计算了含有一个摩擦连接的梁在正弦激励下的稳态解，其连接处摩擦力用库伦模型来描述，得到的数值计算结果与实验结果吻合.Ding等［6］提出了用于计算含有库伦摩擦阻尼器的单自由度振子系统响应的解析计算方法.

库伦模型只能用来描述接触面的粘滞状态和宏滑移状态，而不能用于描述微滑移状态.而实际上，在连接处若产生宏滑移，常会引起连接失效，其并不多见；而微滑移现象更为普遍，它是结构阻尼的重要来源且不会引起连接失效［7-8］，因此其更具研究价值.目前，国内外学者已发展了多种可以描述接触面宏滑移和微滑移的迟滞模型，如Iwan模型［9］、Valanis模型［10］以及Bouc-Wen模型［11-12］等.其中，Iwan模型由于其构型简单直观，近年来颇受关注，已被广泛应用于研究含摩擦连接结构的力学行为和阻尼问题［13-16］.图1（a）和（b）分别是经典Iwan模型和改进Iwan模型构型示意图.经典Iwan模型是由N个Jenkins单元并联而成，每个Jenkins单元（也称为双线性迟滞模型）是由刚度为ki的线性弹簧和屈服力（即临界摩擦力）为fi∗的库伦摩阻片串联构成.修正Iwan模型是在经典Iwan模型的基础上并联一个弹簧单元得到的.由于每个Jenkins单元的屈服位移xi∗（xi∗=fi∗／ki）不同，使得Iwan模型可以用来描述连接处的宏滑移行为（所有Jenkins单元产生滑动）和微滑移行为（部分Jenkins单元出现滑动）.

图1 Iwan模型示意图

本文研究的是由有限个Jenkins单元构成的Iwan模型的摩擦振子在简谐激励下的响应求解问题.针对此类分段线性的振子系统，在文献［6］中方法的基础上，给出了简谐激励下振子系统响应的精确解析求解方法，并分析系统在不同量级的外激励下的动力学特征和阻尼特性.

1 摩擦振子模型

本文研究的振子模型如图2所示，模型为刚度kα，粘性阻尼c，质量块m的振子系统.在外部简谐激励Fesin（ωt）的作用下，质量块将沿摩擦面上运动，位移为x.基于Iwan模型描述的摩擦接触模型见图3：图中，ui为Iwan模型中任意一个摩阻片的位移.系统的运动方程为

其中，｛ui｝是各摩阻片位移的集合，f（x，x，｛ui｝）是Iwan模型描述的接触面摩擦力函数，如下

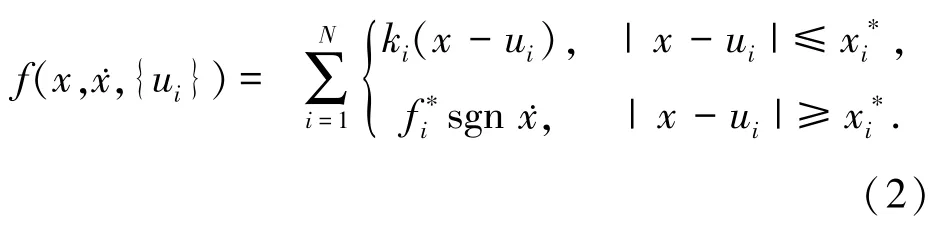
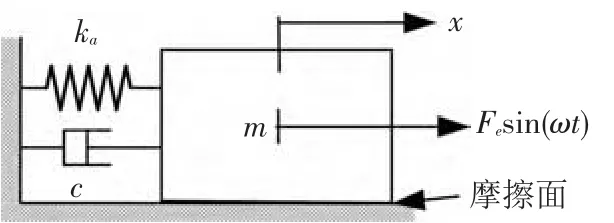
图2 振子模型示意图

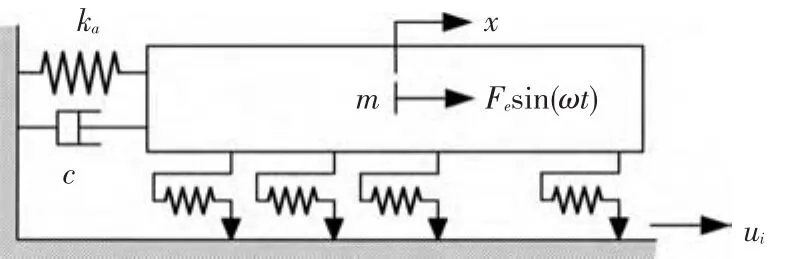
图3 含Iwan摩擦模型的振子模型

当处于粘滞状态时（即所有Jenkins单元均未滑动），系统的总刚度为

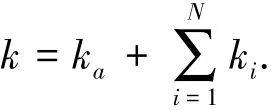
引入下面无量纲化参数

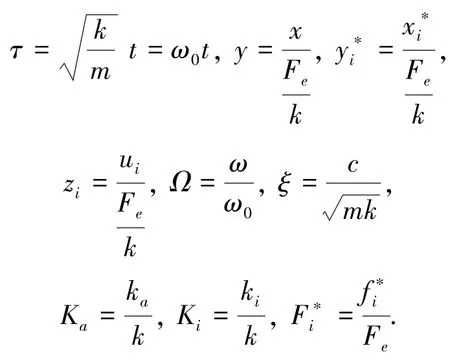
得到无量纲化后的方程（1）为

其中y＇和y″分别表示y对τ的一、二阶导数，F（y，y′，｛zi｝）为无量纲摩擦力函数式如下所示.

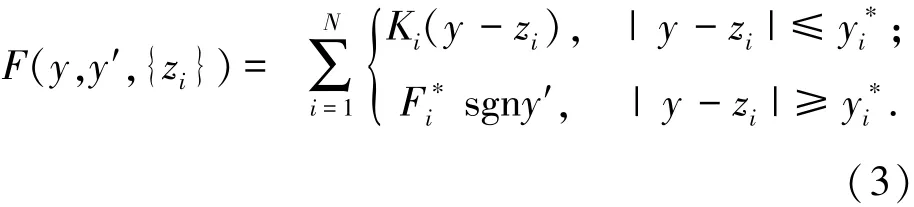
2 振子响应计算

从式（3）可以看出，可根据Iwan模型中发生屈服（滑动）的Jenkins单元数量，将振子每次加载（振子速度为正）／卸载（振子速度为负）的过程分为N+1个阶段，分别命名为S0，S1，S2，…，SN，其中下标i（i=0，1，2，…，N）对应为在该运动阶段已屈服的Jenkins单元的数量.在每个阶段内，振子的刚度不变，其恢复力-位移关系是线性的.在周期外载荷激励下，振子反复经历加载和卸载过程，在任意一次加载／卸载过程中，如果接触面存在滑动，系统将历经多个运动阶段.下面任取一个加载／卸载过程中的一个阶段的运动进行分析.

2.1 各阶段的运动方程

将所有Jenkins单元的屈服位移按从小到大排列，则对于任意运动阶段Si，无量纲位移满足

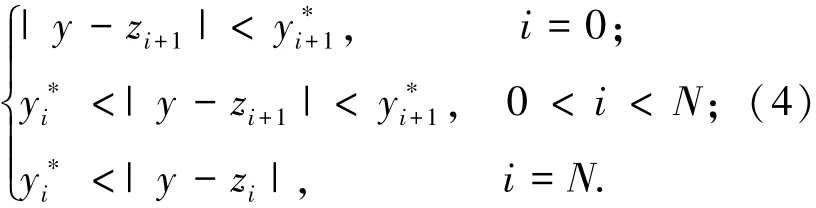
接触面摩擦力可写成

式中F（y＇，｛zi｝）为常数项，Kires为阶段Si中Iwan模型的剩余刚度，两者分别为

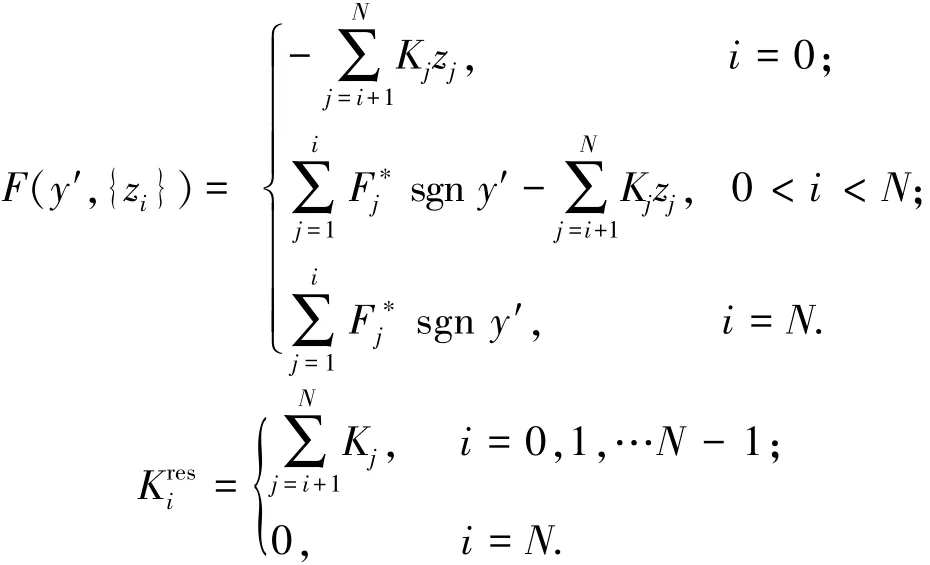
将式（5）代入式（2），得到阶段Si的运动方程为

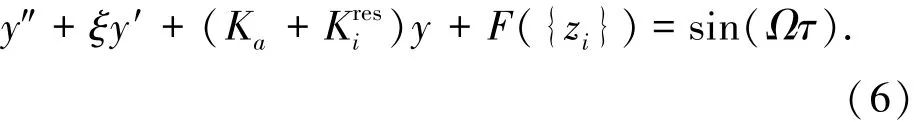
2.2 方程解的一般表达式

假设在τa时刻，运动进入阶段Si，则方程（8）的解可写成下面一般形式

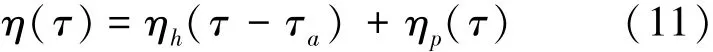
其中ηh为瞬态部分，ηp为稳态部分，它们各自为

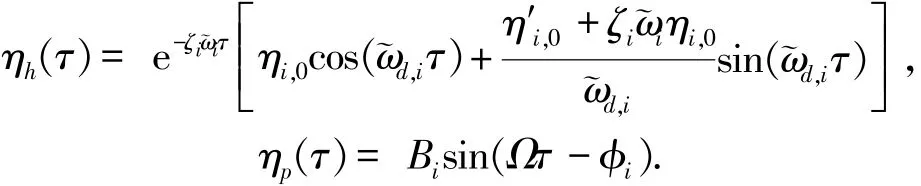
式中

很明显，当λi=1时，Bi达到最大值1／（2~），亦即1／（ξΩ）.

当初值ηi，0与η′i，0已知时，便可求得该运动阶段内任意时刻的η（τ）值，代入式（7）便可进一步求得位移y（τ）.假设Si的前一个运动阶段的系统响应已知，由速度和位移在τa处的连续性，容易求得初值ηi，0与η′i，0分别为

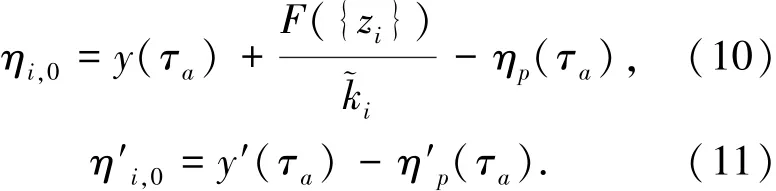
2.3 摩阻片位移值计算

式（10）中变量｛zi｝尚未求得.将构成Iwan模型的Jenkins单元按屈服位移从小到大依次命名为J1、J2、…、JN，并将Si所处的加载／卸载过程的初始时刻和末端时刻分别标记为τ01和τ02.则在运动阶段Si中，Jenkins单元J1至Ji屈服，其余均处于粘滞状态.对于处于粘滞状态的单元，其摩阻片在该阶段任意时刻的位移值与加载／卸载初始时刻的位移值相同：

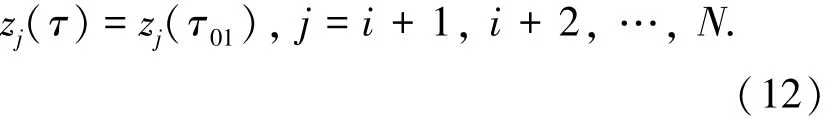
而对于已滑动的单元，在Si阶段滑动的位移与振子在该阶段振子运动位移相同，因此

式（15）表明，每次加载／卸载过程中，初始时刻各摩阻片的位移值正是式（10）中待求的｛zi｝，因此只需求得这些时刻已屈服单元中摩阻片的位移值即可.假设当前加载／卸载过程中，振子的运动经历了S0到Sn（n≤N）的阶段，且zj（τ01）已知，结合式（13）不难求出τ02时刻（下一个卸载／加载初始时刻）各摩阻片的位移值为

式（14）也可视为每次加载／卸载完成后，库伦摩阻片位移值的更新.由于零时刻点摩阻片的位移值已知，则第一个加载／卸载过程内振子的位移值便可求得，下一个卸载／加载过程初始时刻摩阻片的位移值可通过式（14）～（15）求得，依次递推求解，便可获得整个时域内振子响应和每次加载／卸载初始时刻各个摩阻片的位移值.

2.4 阶段转换时刻的确定

确定阶段转换时刻，就是确定各个运动阶段的初始时刻和末端时刻，如式（9）～（11）中的τa，该值显然会影响解的精度.当不等式（4）不再满足时，运动跳出阶段Si，转入其他运动阶段.这里存在两种情况，如果

运动进入阶段Sj，如果速度为零

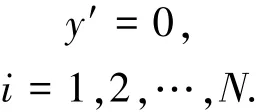
则所有Jenkins单元全部停止滑动，运动转入S0.为了确定状态转换时间，我们构造下面函数

以及

不难看出，确定状态转换时刻实际上就是寻找g1（τ）或g2（τ）的零值点所对应的时刻值，亦即为求方程g1（τ）=0或g2（τ）=0的根.在每一步的计算过程中，应首先判断g2（τ）是否经过零值点：如果过零，则状态转入S0；如果未过零，进一步判断g1（τ）：如果过零，则转入更高阶段Sj，如果未过零，则进行下一步计算.为了获得更准确的两函数零值点所对应的时间值，当g1（τ）或g2（τ）处于零值附近时，应减小步长，可用二分法确定零值点所对应的时刻值.

从前面分析过程不难看出，本文提出的方法是一种“分段-解析”法：先对分段线性运动方程（2）进行分段分析，由于各运动阶段内的运动方程（6）都是线性的，通过变量代换（式（7）），便获得了代换后方程的精确解析解（9），这样顺次求得相应时域内各个阶段运动方程的解析解，自然获得了所求时域上振子系统的响应.由于式（9）为线性方程（8）完全精确的解析解，而方程（8）是通过对方程（6）进行变量代换得到的，变量代换显然不会引入误差，因而将式（9）代入代换式（7）所得的解便是方程（6）的精确解析解.由此可见，如果阶段转换时刻能精确确定，由各阶段的精确解析解连接起来所形成的方程（2）的解便完全精确.但由阶段转换时刻只能通过数值方法确定，这个过程不可避免会产生数值误差，其误差大小由事先设置的误差容限（迭代终止条件）决定.因此，这里的“分段-解析”法的误差仅来源于确定阶段转换时刻的数值误差，这种误差显然要远小于求解非线性振动方程的近似解析方法（如谐波平衡法、小参数摄动法等）由近似所致的误差.与纯数值方法相比（如用四阶龙格库塔法直接求解方程（2）），该“分段-解析”法可给出每个运动阶段所对应方程的精确解析解，因此比数值方法更精确和高效.需要说明的是，当Jenkins单元数量非常大而趋于无穷时，其振子系统不再是分段线性系统，这种情况下，本文方法不再适用.

3 仿真算例及结果讨论

假设Iwan模型中Jenkins单元的刚度和屈服位移满足下面关系：

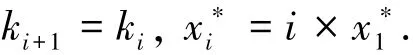
模型参数见表1.

表1 模型参数

取方程参数为表1中的数据，由上节介绍的方法求得的大约30个周期的无量纲位移、速度和摩擦力的时间历程如图4所示.从图中可以看出，由于摩擦阻尼的影响，使得系统运动很快进入稳态.图5为图4中位移和摩擦力稳态阶段一个周期时域曲线的放大图，曲线上的圆圈为阶段转换点.可以看出，在该量级的激励下，在一个加载／卸载过程中依次经历了S0到S4的5个运动阶段.从图还可看出，每个转换点前后位移曲线光滑性要好于恢复力曲线，这是由于恢复力变化量是刚度与位移变化量的乘积，因此阶段转换引起的刚度变化对其影响较大.以图5中位移和摩擦力分别为x轴和y轴，便得到了如图6所示的迟滞环曲线，曲线的斜率值表示了每个运动阶段内系统的刚度.很明显，在S4阶段，Iwan模型恢复力值为定值，Iwan模型刚度为零，表明Iwan模型中所有Jenkins单元均屈服，模型处于宏滑移阶段.

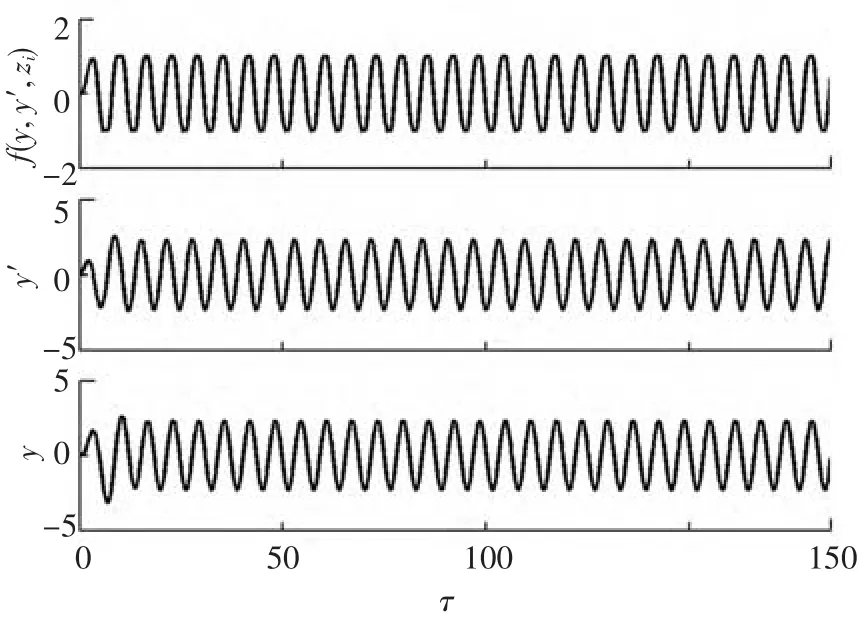
图4 振子无量纲位移、速度和恢复力时间历程图

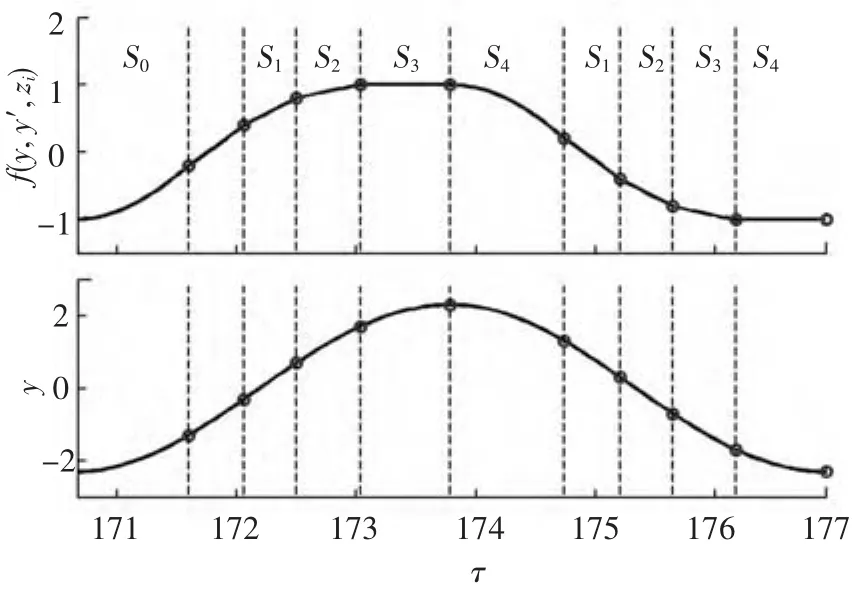
图5 振子稳态阶段一个周期内位移、速度和摩擦力的时域曲线

图6 系统稳态段迟滞环

图7是不同激励幅值下，激励频率在［0.1，1.5］区间内振子系统响应的幅频曲线.图中，γ=Fe／1.579 1.结果显示，当γ=0.2时，其幅频曲线峰值出现在Ω=1处，其值为20，正好等于Bi的极值1／（ξΩ），表明在此激励下，整个振动周期内F（y′，｛zi｝）均为零，表明振子运动一直处于S0阶段，因此振子运动是完全线性的.故该幅频曲线也是线性的.

比较图中的曲线可发现：随着激励力幅值增大，曲线峰值明显左移，表现出刚度软化特征，其原因显而易见：激励力幅值越大，产生屈服Jenkins单元越多，系统刚度递减量就越大.从图中还可发现，随着激励力幅值的增大，幅频曲线的峰值先减小后增大，表明系统阻尼也随之先减小后增大.文献［17］中的实验结果也出现了此现象，但作者并未给出解释.显然这种阻尼特征是由Iwan模型决定的，由于Iwan模型是由一系列Jenkins单元并联而成，故其阻尼特性与单个Jenkins单元的阻尼特性密切相关.对于任意一个Jenkins单元，在简谐激励下发生屈服时的迟滞环的形状如图8所示，图中A为振幅.当振动频率为ω时，Jenkins单元的等效粘性阻尼为

对A求偏导，得到

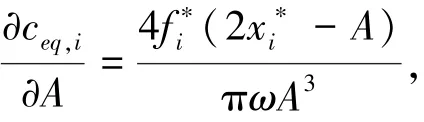
可见，在区间（xi∗，+∞）上，ceq，i随A先增后减，当A的值为2xi∗时，ceq，i有最大值为

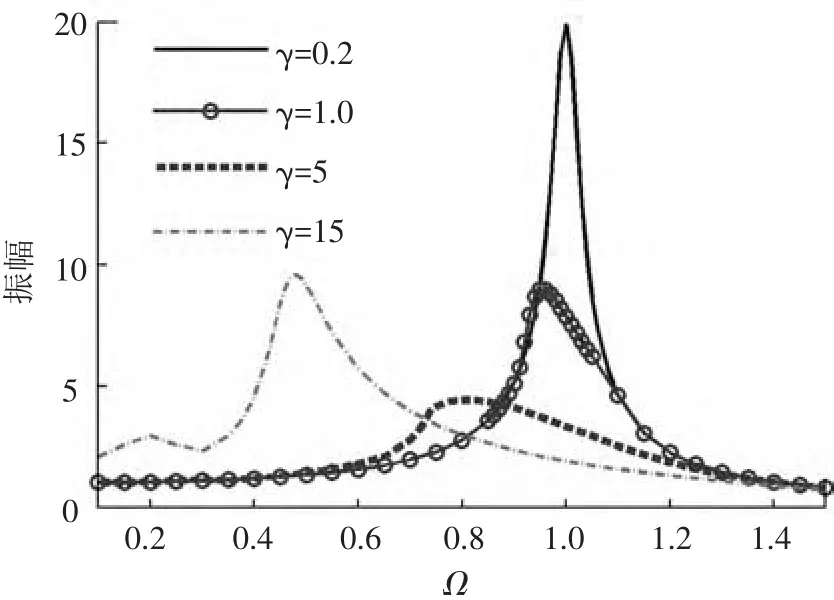
图7 不同量级外激励下的振子响应的幅频曲线

图8 单个Jenkins单元的迟滞回线示意图

而Iwan模型的等效粘性阻尼为

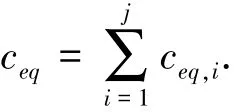
可见，Iwan模型的等效粘性阻尼也会随着振幅的增大而先增大后减小.γ=15对应的幅频曲线上共振带边缘频率点Ω=0.4和Ω=0.6处所对应的稳态段的迟滞环形状如图9所示.可以看出，在一个运动周期的大部分时间内，Iwan模型处在宏滑移阶段（即S4阶段），迟滞环形状与双线性迟滞模型的迟滞环形状（图8）相似，且振幅远大于Iwan模型中屈服位移值最大的J4的屈服位移的2倍，因此其等效阻尼值已经出现减小.

图9 当γ＝15，Ω＝0.4和Ω＝0.6时分别对应的迟滞环

4 结 论

针对简谐激励下一类含Iwan模型的分段线性振子系统的非线性振动问题，提出了用于计算系统响应的“分段-解析”方法.通过对一算例求解，分别得到了系统响应的时域曲线和幅频曲线.在激励量级逐渐递增时，幅频曲线峰值明显向左偏移，使得Jenkins单元滑动所致的刚度软化效应得到了体现.另一方面，摩擦阻尼对系统响应影响也很显著：随着激励量级的递增，幅频曲线峰值先减小后增大.通过对构成Iwan模型的Jenkins单元的等效粘性阻尼分析，得到系统等效粘性阻尼随振幅的增大而先增大后减小，从而解释了幅频曲线峰值产生这种变化的原因.文中方法为存在分段线性问题的系统的响应求解提供了一种有效途径.后面还可进一步开展关于存在摩擦连接边界的连续体的非线性振动方面的研究.

［1］肖世富，陈滨，杜强.宽带随机激励下非线性连接结构振动响应分析［C］／／第十三届全国结构工程学术会议论文集（第Ⅰ册）.井冈山：中国力学学会结构工程专业委员会，2004：405-411.

［2］BEARDS C F.Damping in structural joints［J］.The Shock and Vibration Digest，1992，24（7）：3-7.

［3］IBRAHIM R，PETTIT C.Uncertainties and dynamic problems of bolted joints and other fasteners［J］.Journal of Sound and Vibration，2005，279（3／4／5）：857-936.

［4］DEN HARTOG J P.Forced vibrations with combined Coulomb and viscous friction［J］.Journal of Applied Mechanics，ASME，1931，53（9）：107-115.

［5］LEE Y，FENG Z C.Dynamic responses to sinusoidal excitations of beams with frictional joints［J］.Communications in Nonlinear Science and Numerical Simulation，2004，9：571-581.

［6］DING Q，CHEN Y.Analyzing resonant response of a system with dry friction damper using an analytical method［J］.Journal of Vibration and Control，2008，14（8）：1111-1123.

［7］GUTHRIE M A，KAMMER D C.A general reduced representation of one-dimensional frictional interfaces［J］.Journal of Applied Mechanics，ASME，2008，75（1）：011019.

［8］CHEN W，DENG X.Structural damping caused by micro-slip along frictional interfaces［J］.International Journal of Mechanical Sciences，2005，47（8）：1191-1211.

［9］IWAN W D.A distributed-element model for hysteresis and its steady-state dynamic response［J］.Journal of Applied Mechanics，ASME，1966，33（4）：893-900.

［10］VALANIS K C.Fundamental consequences of a new intrinsic time measure：plasticity as a limit of the endochronic theory［J］.Archiwum Mechaniki Stossowanej，1980，32（2）：171-191.

［11］BOUC R.Forced vibration of mechanical system with hysteresis［C］／／Proceedings of the Fourth Conference on Nonlinear Oscillations.Prague：［s.n.］，1967.

［12］WEN Y K.Method of random vibration of hysteretic systems［J］.Journal of the Engineering Mechanics Division，ASCE，1976，102（2）：249-263.

［13］OUYANG H，OLDFIELD M J，MOTTERSHEAD J E.Experimental and theoretical studies of a bolted joint excited by a torsional dynamic load［J］.International Journal of Mechanical Sciences，2006，48（12）：1447-1455.

［14］SEGALMAN D J.A modal approach to modeling spatially distributed vibration energy dissipation，Technical Report No.SAND2010-4763［R］.New Mexico：Sandia National Laboratories，2010.

［15］ARGATOV I I，BUTCHER E A.On the Iwan models for lap-type bolted joints［J］.International Journal of Non-Linear Mechanics，2011，46（2）：347-356.

［16］QUINN D D.Modal analysis of jointed structures［J］.Journal of Sound and Vibration，2012，331（1）：81-93.

［17］JALALI H，AHMADIAN H.Identification of microvibro-impacts at boundary condition of a nonlinear beam［J］.Mechanical Systems and Signal Processing，2011，25：1073-1085.