基于ZPETC-FF和DOB的精密运动平台控制

陈兴林，刘 川，周乃新，王 斌

（哈尔滨工业大学航天学院，150001哈尔滨）

光刻机的工件台和掩模台是高动态精密伺服运动平台，它要求在高速运动的情况下，采用长行程直线电机宏动跟随平面电机高精密微动的驱动方式，在较短的行程内实现平台高精度的定位与跟踪.以ASML已经商用的最先进光刻机Twinscan XT 1950i机型为例，工作时最高速度大于0.5 m／s，加速度大于15 m／s2，定位精度小于4 nm，稳定时间小于10 ms［1］.为减小平面电机的运动范围和加速度，就必须提高直线电机宏动精密运动平台的轨迹跟踪精度，因此，选择一种能够抗击干扰，提高系统动态性能，减小系统稳定时间，准确控制宏动精密运动平台运动的算法显得尤为重要.

在光刻机的宏动台伺服系统中，系统中的扰动会造成伺服性能的下降，如：齿槽效应、端部效应力、摩擦力、纹波推力等非线性因素［2］，因此对宏动精密运动平台的控制系统性能提出了更高的要求.在提高系统动态跟踪性能方面，Tomizuka M［3］提出了零相位跟踪控制器（zero phase error tracking controller，ZPETC），其基本思想是基于零极点对消来抑制系统延迟而引起的相位误差，并针对那些具有不稳定零极点的系统，在抵消掉不稳定零点之后，ZPETC再补偿这些零点产生的相位移，最终获得零相位误差.但是，ZPETC在具有上述优点的同时，存在着对系统建模误差和对系统参数变化敏感的缺点.为此，赵希梅［4］提出将ZPETC和干扰观测器（disturbance observer，DOB）［5］相结合的方法，仿真得出了很好的效果.Tsu-Chin Tsao等又提出自适应零相位跟踪控制算法［6］，通过系统参数的自适应辨识来建立模型.K.Ohishi等［7］提出一种零相位误差跟踪（zero phase error tracking，ZPET）和前馈（feed forward，FF）控制相结合的控制方法，并将此ZPET-FF方法应用于磁道跟踪伺服控制中.

本文提出将ZPETC-FF和DOB相结合的方法应用到精密运动平台的控制中，首先建立精密运动平台的控制模型，其次规划平台五阶S曲线运动轨迹，再给出ZPETC-FF和DOB相结合的具体算法，最后通过实验验证该方法的有效性.

1 精密运动平台控制模型

本文研究的精密运动平台只针对宏动台，微动台固定在宏动台上不动.宏动台由气浮导轨导向，直线电机驱动，用光栅尺测量台体与基础框架之间的位移x作为位置反馈.考虑平台中各质量块连接刚度足够，建立等效模型示意图，如图1所示.其中，m为直线电机动子上的总质量，F为直线电机力输入，c为阻尼系数.因为系统由气浮导轨支撑，所以台体与气浮台面之间的刚度k，可以忽略不计.

图1 运动平台机械模型

直线电机因为其结构和负载形式的不同，其数学模型差别较大［8-11］，本文结合直线电机的具体结构和负载形式，建立如下的数学模型：

式中：i（t）为直线电机线圈回路中的电流输入；Fd为推力扰动；km表示直线电机的力常数.

式中：U（t）表示加在直线电机动子线圈两边的电压；E表示线圈移动时产生的反电势；R表示线圈回路电阻；L表示线圈回路电感.

式中ke表示和速度有关的反电动势系数.联立解式（1）～（4），可得到直线电机位移与控制电压之间的传递函数为

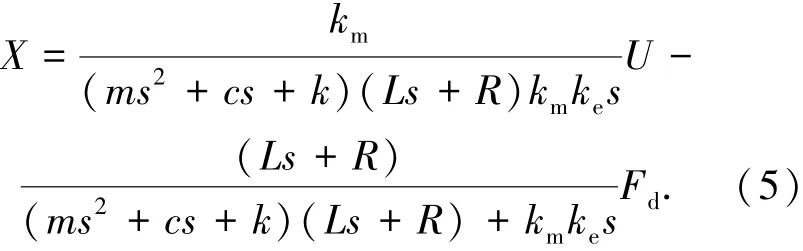
2 轨迹规划

为达到高精度点对点轨迹规划，采用五阶S曲线轨迹.相比低阶轨迹，五阶轨迹的轨迹轮廓更光滑，对基础框架冲击更小，振动更少，达到的位置精度更高［12］.图2所示为一种典型的五阶加速轨迹，改变给定的约束条件，amax，jmax，dmax和fmax都可能不存在，因此轨迹规划存在很多种可能情形.各时间段计算公式见式（6）～（10）.

图2 五阶点对点运动轨迹

式中f0、d0、j0、a0、v0、x0为初始边界条件，t为时间.

3 精密运动平台控制器结构

精密运动平台的控制器结构如图3所示，包括双环PID控制、ZPETC-FF和DOB.双环PID控制器设计了速度环控制器和位置环控制器，采用二自由度控制系统可以在保证系统稳定性及抗干扰能力的情况下，通过配置系统零极点提高系统的动态响应能力.

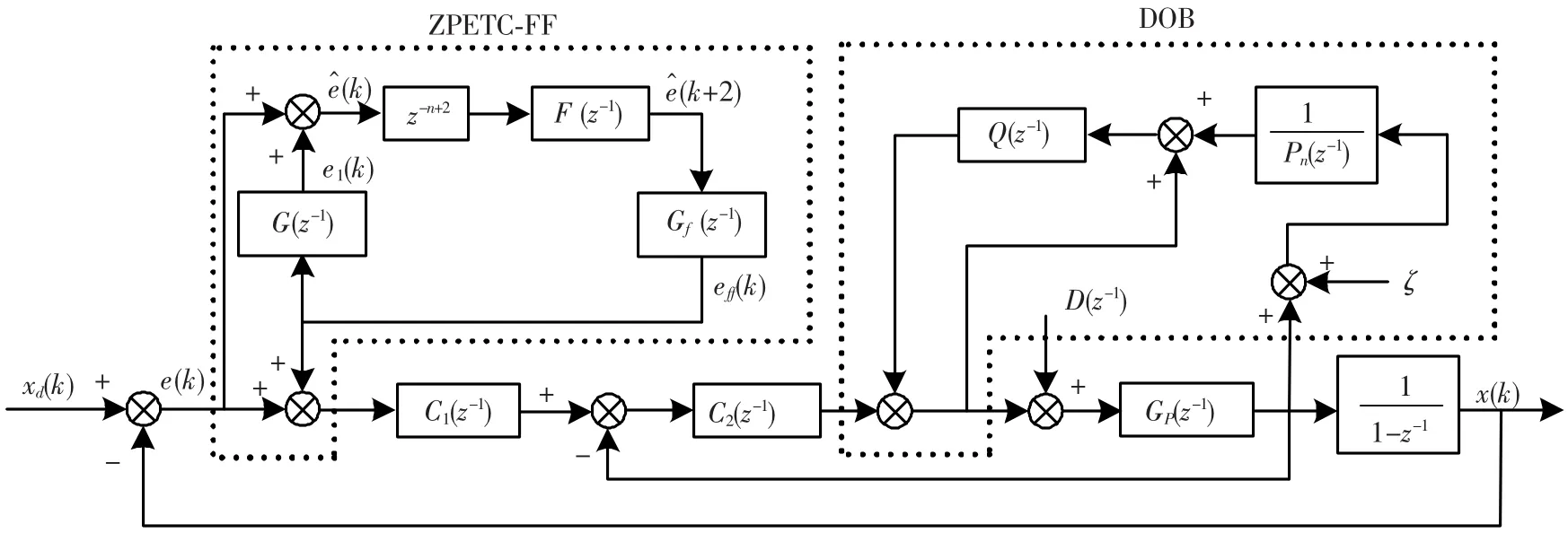
图3 运动平台控制器结构

3.1 ZPETC-FF的设计

前馈控制器采用ZPETC的原理设计，反馈控制则运用两个PID反馈控制器来实现，其传递函数分别为C1（z-1）和C2（z-1）.ZPETC-FF控制器由信号估计器G（z-1）（signal estimator）、储存器z-n+2（memory）、低通滤波器F（z-1）（LPF）和预校正器Gf（z-1）（Pre-compensator）等几个部分组成.

由图3可知，反馈控制系统的闭环系统传递函数为

式中：z-d为闭环系统所造成的d步延迟；Bc+（z-1）为稳定的零点多项式，Bc-（z-1）为不稳定的零点多项式.

前馈控制系统中的Gf（z-1）传递函数为

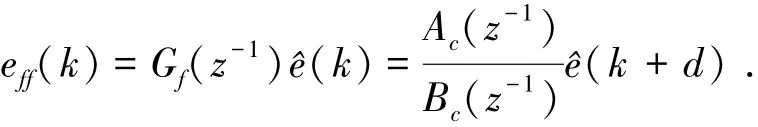
由上式可见，ZPETC是非因果的，在运用时至少要提前1步获得指令，也就是超前两个采样周期的信号（d=2）.

图3中z-n+2中的n为储存器的大小，它和两个采样时间之前的台体运动周期匹配，将以前控制周期内的控制信号作为未来时刻的值，从而实现对系统的重复控制.F（z-1）为低通滤波器，用于消除跟踪误差信号中的高频噪声.G（z-1）用于估计出系统的稳态跟踪误差，以计算Gf（z-1）.图3中的控制系统，满足以下等式：

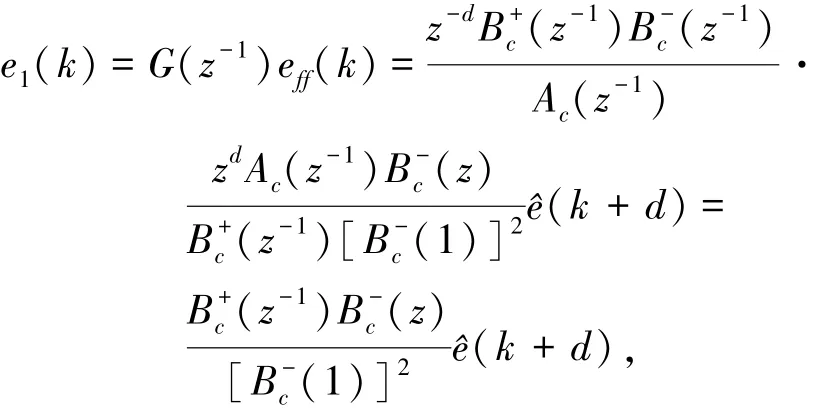
并且有

由此可得系统的跟踪误差为

利用欧拉公式ejωT=cosωT+jsinωT，将复数序列由指数形式转变成三角函数形式可知，当z=ejωT时，表达式Bc+（z-1）Bc-（z）／［Bc-（1）］2的相位差为0；当ω趋近于0时，z趋近于1，则有Bc+（z-1）Bc-（z）／［Bc-（1）］2的幅值也趋近于1，所以系统的跟踪误差收敛于0.

3.2 DOB的设计

DOB的基本原理就是将外部力矩干扰及模型参数变化造成的实际对象与名义模型的逆P-1n（s）的输出的差异，等效到控制输入端，即观测出等效干扰，在控制中引入等量的补偿，实现对干扰的完全抑制.DOB的原理如图4所示.

图4 DOB的原理框图

图中，Gp（s）为对象的传递函数，Gn-1（s）为名义系统模型Gn（s）的逆，u为速度环的给定输入信号，d为系统的外部干扰，为干扰的估计量，ξ为测量噪声，P（s）为实际对象的传递函数，Q（s）为低通滤波器.

由图4求出等效干扰的估计值及从u到y的传递函数GUY（s）分别为

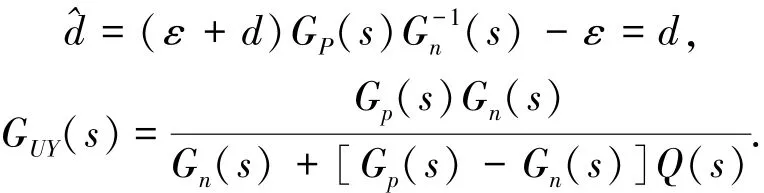
将图4作等效变换，可得到简化的框图，如图5所示.

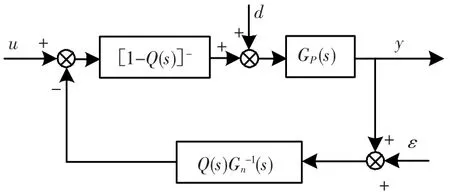
图5 原理图等效变换

由图5可求得从d到y的传递函数GDY（s）和从ε到y的传递函数Gεy（s）分别为

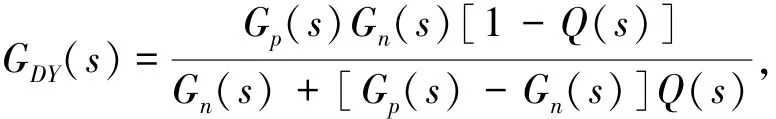
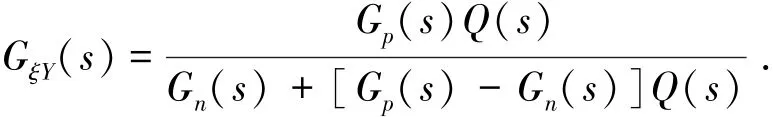
图5表明，这个扰动估计与补偿系统本身也是一个反馈回路，系统的带宽要受到鲁棒稳定性的限制，所以Q（s）的带宽也不能太宽，要在扰动抑制和鲁棒稳定性之间找一个折中，另外，Q（s）的设计要满足Q（s）Gn-1（s）为正则.在本文中，Q（s）为3阶滤波器，时间常数取为τ=0.002，则

在低频段时，Q（s）→1，有

在高频段时，Q（s）→0，有

可以看出，在低频段时，DOB使得实际对象的响应与名义模型的响应一致，实现了对实际模型与名义模型偏差的补偿.

4 实 验

图6为实验系统，精密运动平台电机采用线性无刷直线伺服电机BLMC-192-A，行程为200 mm，母线最高电压320 VDC，运动位置由RENISHAW公司的XL-80激光干涉仪测得，其定位精度±1 nm，线性测量精度±0.5×10-6；运动控制卡为自制版卡，采用TI公司的TMS320C6416型DSP芯片，主频1 GHz；运动平台质量m为38 kg.反电动势常数ke为26.89 V／m／s，力常数km为33.09 N／A，25℃时电阻值R为6.4 Ω，电感值L为1.9 mH.

图6 实验系统实物图

精密运动平台要跟踪的五阶S曲线参数如表1所示，拟合出的曲线见图7.图8为只有PID控制时，运动平台跟踪五阶S曲线的跟踪误差，在加减速时，最大误差为0.16 mm；在速度为匀速时，最大误差为0.05 mm.此时系统跟踪误差较大是因为系统中没有滤波器，引入了很多的噪声，而且没有前馈补偿，带宽有限，最终导致控制误差偏大.

表1 五阶S曲线参数

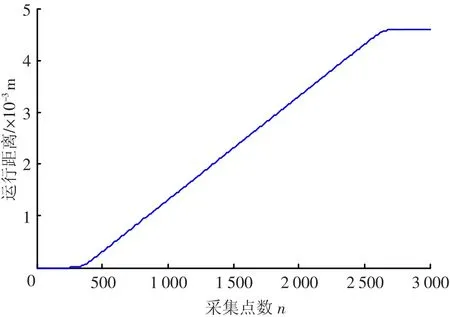
图7 五阶S曲线

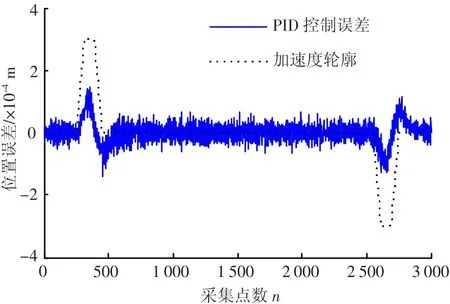
图8 PID控制下的误差曲线

图9为速度和加速度前馈、PID和DOB复合控制下的跟踪误差曲线，图10为图9局部放大的误差曲线.在引入干扰观测器后，系统中的未知扰动和测量噪声得到有效抑制，并对扰动进行估计和补偿，使控制误差明显减小.在加减速时，最大误差为0.8 μm；在匀速运行时，误差逐步减小，在第670个采样点附近，系统趋于稳定，误差始终保持在一定范围内，最大误差为0.03 μm.

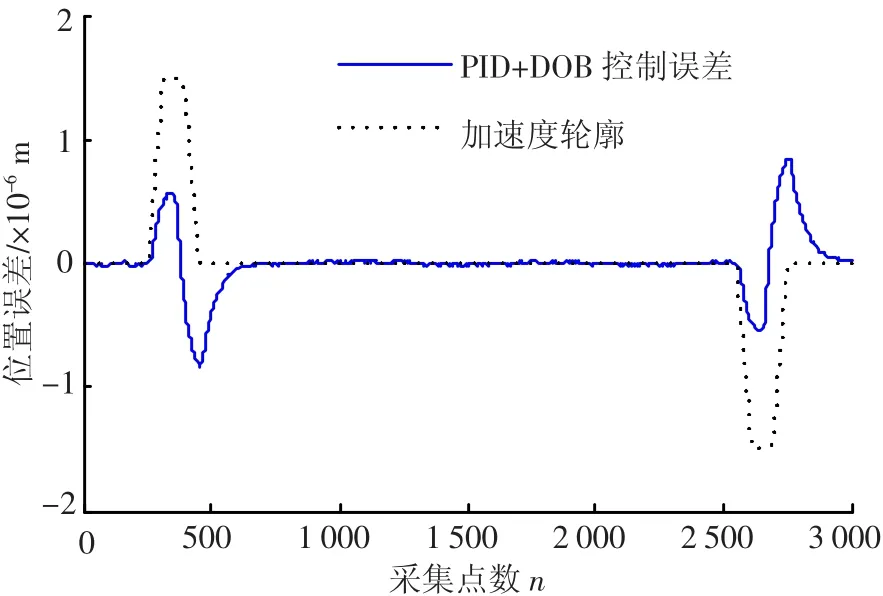
图9 PID＋DOB控制下的误差曲线

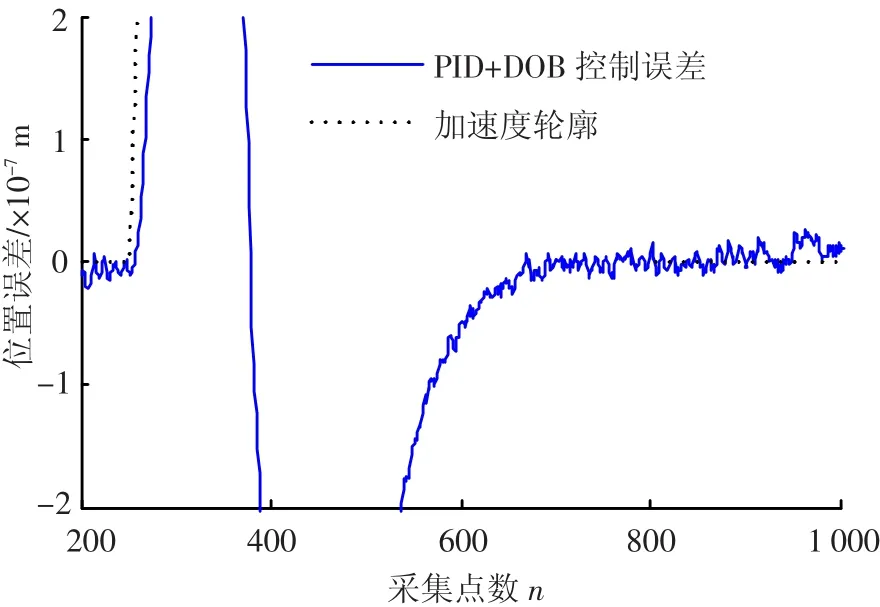
图10 放大的误差曲线（PID＋DOB）

图11为ZPETC-FF、PID和DOB复合控制下的轨迹跟踪误差曲线，图12为图11局部放大的误差曲线.在加减速时，最大误差为0.5 μm；在匀速运行时，误差逐步减小，在第500个采样点附近，系统趋于稳定，误差始终保持在一定范围内，最大误差为0.02 μm.误差减小的原因主要有以下两点：1）台体的运动轨迹已经规划好，ZPETCFF预先获得位置指令，将控制指令提前，并且不断重复修正，所以跟踪误差减小，系统稳定时间也减小；2）ZPETC-FF是一种非因果的前馈控制器，提高了系统位置闭环带宽，减小了加减速时的位置跟踪误差，提高了系统控制精度.

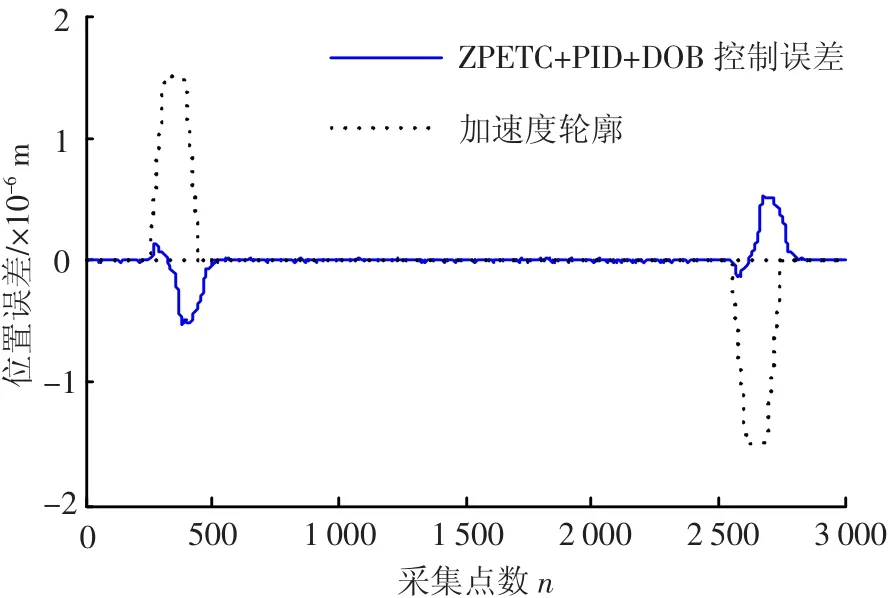
图11 ZPETC-FF＋PID＋DOB控制下的误差曲线

在图9～12中，宏动台在加减速运动时，存在误差峰值，且峰值幅度随速度的增大而增大，原因主要有以下4点：1）电机加减速时，控制指令加减速变化较大，引起绕组电流变化，导致磁阻推力相应变化，从而造成较大位置误差；2）直线电机加减速时，系统冲击较大，电机定子存在较大惯性时滞.台体减速时的误差要小于台体加速时的误差，这是因为台体从高速开始逐步减速时，具有较大的惯性，其运动惯性极大地阻尼掉了磁阻推力的干扰影响，这是实验结果中台体在减速时位置误差相对较小的主要原因.3）台体的运动轨迹为5阶S曲线，系统即有5阶输入指令，在前馈没有完全物理实现的情况下，低阶系统不能够完全跟踪5阶高阶输入指令，系统必然存在静差，从而在加减速时产生相比匀速时更大的位置偏差.4）前馈补偿的式子一般均具有比较复杂的形式，故全补偿条件的物理实现有困难.在工程实际中，大多采用满足跟踪精度要求的部分补偿条件，或者在对系统性能起主要影响的频段内实现近似全补偿，以使前馈补偿的形式简单并易于物理实现，因此在加减速和匀速时，都存在误差.

通过对比3种控制策略的位置跟踪误差曲线，发现采用ZPETC-FF+PID+DOB的控制策略的系统误差更小，系统达到的精度更高，验证了该方法的有效性.

图12 放大的误差曲线（ZPETC-FF＋PID＋DOB）

5 结 论

本文针对精密运动平台系统，提出了基于ZPETC-FF和DOB相结合的复合控制策略，通过实验验证了该方法的有效性.结论如下：

1）对于轨迹预知的系统，ZPETC-FF能够提高系统的带宽和跟踪能力，减小系统稳定时间，使系统达到一个很高的精度.

2）DOB作为鲁棒反馈控制器，能够有效抑制干扰和补偿系统扰动.

3）采用ZPETC-FF、DOB和PID相结合的复合控制方式，可以在保证系统稳定性及抗干扰能力的同时，提高系统的动态响应能力，此控制模型可以推广到其他轨迹预知的控制系统.

实验结果表明，该方法满足光刻机工件台对伺服驱动系统的高速、高精度轨迹控制要求.

［1］SCHMIDT R H.Ultra-precision engineering in lithographic exposure equipment for the semiconductor industry［J］.PhilosophicalTransactionsoftheRoyalSocietyA：Mathematical，Physical and Engineering Sciences，2012，370（1973）：3950-3972.

［2］孙宜标，闫峰，刘春芳.基于μ理论的永磁直线同步电机鲁棒重复控制［J］.中国电机工程学报，2009，29（30）：52-57.

［3］TUMIZUKA M.Zero phase error tracking algorithm for digital control［J］.ASME Journal of Dynamic Systems Measurement and Control，1987，109（4）：65-68.

［4］赵希梅，郭庆鼎.基于ZPETC和DOB的永磁直线同步电机的鲁棒跟踪控制［J］.中国电机工程学报，2007，27（30）：60-63.

［5］OHNISHI K.A new servo method in mechatronics［J］.IEEE Transaction son Electrical and Electronic Engineering，1987，107（D-1）：83-86.

［6］TSAO T C，TOMIZUKA M.Adaptive zero phase error tracking algorithm for digital control［J］.Journal of Dynamic System，Measurement and Control，1987，109（4）：349-354.

［7］OHISHI K，MIYAZAKI T，INOMATA K，et al.Robust feed-forward tracking servo system considering force disturbance for the optical recording system［J］.IEEE Trans.Ind.Electron，2006，53（3）：838-847.

［8］陈幼平，杜志强，艾武，等.一种短行程直线电机的数学模型及其实验研究［J］.中国电机工程学报，2005，25（7）：131-136.

［9］YAN M，HUANG K，SHIU Y，et al.Disturbance observer and adaptive controller design for a linearmotor-driven table system［J］.International Journal of Advanced Manufacturing Technology，2007，35（3／4）：408-415.

［10］LI S H，LIU Z G.Adaptive speed control for permanent magnet synchronous motor system with variations of load inertia［J］.IEEE Transactions on Industrial Electronics，2009，56（8）：3050-3059.

［11］武志鹏，陈兴林，刘川.光刻机工件台宏微系统的滑模变结构控制［J］.光电工程，2011，38（9）：50-54.

［12］武志鹏，陈兴林.精密硅片台步进扫描运动的5阶S曲线规划［J］.光电工程，2012，39（8）：99-104.