过驱动航天器自适应姿态补偿控制及控制分配

张爱华，胡庆雷，霍 星

（1.哈尔滨工业大学 控制科学与工程系，150001哈尔滨；2.渤海大学 工学院，121013辽宁锦州）

针对存在外部干扰及不确定转动惯量的航天器姿态控制问题，国内外众多学者开展了大量的研究.如文献［1］基于自适应可控制理论设计了一种姿态跟踪控制算法，解决了执行器输出力矩饱和与外部干扰问题.文献［2］针对存在不确定转动惯量的航天器姿态跟踪问题，提出一种自适应控制策略.但上述文献［1-2］仅能单一处理外部干扰或者不确定转动惯量问题.进而，文献［3］针对刚体航天器同时存在系统不确定参数与干扰问题，考虑推力器故障，设计了自适应容错控制器.此外，文献［4］设计一种不依赖于转动惯量的姿态控制器.文献［5］设计了姿态输出反馈跟踪控制器.文献［6］针对惯量特性未知、存在外部干扰与控制力矩受限的姿态跟踪问题，设计了一种自适应控制器以实现对期望姿态的一致最终有界跟踪控制.

尽管上述文献所提出的姿态控制方法能够解决航天器转动惯量不确定性与外部干扰问题，但它们并没有考虑执行机构安装偏差问题.在实际的航天工程中，受限于安装技术以及发射过程中运载器振动的影响，航天器执行机构的安装偏差不可避免.而这种安装偏差的存在将对姿态跟踪性能产生影响，严重时将使整个姿态控制任务失败.目前对执行器安装偏差问题的相关研究鲜见报道.虽然文献［7］针对推力器安装存在偏差的卫星编队控制问题设计了一种自适应控制器，以实现对这种安装偏差的补偿控制，但该方法并不适用于反作用飞轮控制器的航天器.

为此，本文在上述研究成果的基础上，针对存在外部干扰、不确定转动惯量以及执行机构安装偏差的过驱动刚体航天器姿态跟踪问题，提出一种自适应姿态补偿控制策略，实现对姿态跟踪闭环系统几乎全局渐近稳定控制.同时以能源消耗为优化目标，提出基于能量最优约束动态控制分配算法，保证动态控制分配后控制力矩的平稳性和能量优化.仿真结果验证了本文所提控制与分配策略的有效性.

1 数学模型

1.1 航天器姿态动力学

采用姿态四元数法描述的航天器姿态动力学与运动学方程为［4］：

其中ω∈R3为航天器相对于惯性系的角速度在本体系中的投影，姿态四元数Q=［q0qT］T∈R4表示本体坐标系相对于惯性坐标系的姿态，且满足等式q20+qTq=1.u∈R3为作用于航天器本体轴的总控制力矩，d（t）∈R3表示总的外部干扰力矩，J∈R3×3为航天器转动惯量，且记为J=J0+ΔJ，其中J0表示标称转动惯量，而ΔJ表示不确定的转动惯量.I3为3阶单位矩阵，对任意的向量a=[a1a2a3]T，定义a×为

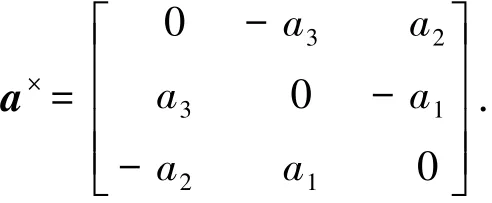
此时，针对姿态动力学方程（3）作如下假设：

假设1转动惯量矩阵J是正定，且存在正常数Jmax满足

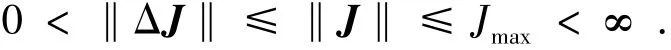
假设2干扰力矩是有界的，存在未知的正常数dmax满足

注1文中‖·‖表示向量的2范数及其诱导范数，‖·‖∞表示矩阵或者向量的无穷范数.

考虑航天器安装N（N＞3）个反作用飞轮进行姿态控制，则此时作用于航天器本体的总控制力矩可计算为

其中D∈R3×N为控制分配矩阵，τ=［τ1τ2…τN］T∈RN为N个反作用飞轮实际输出力矩.

受限于安装技术以及发射过程中振动影响，反作用飞轮将存在小角度的安装偏差.假设航天器反作用飞轮安装偏差矩阵为ΔD，则式（3）可改写成如下形式：

1.2 航天器姿态跟踪数学模型

设航天器期望坐标系T相对于惯性系L的期望角速度为ωd=R3、期望姿态为Qd=［qd0qTd］T∈R4，则有

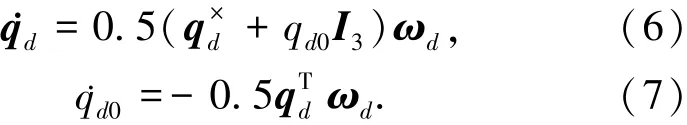
此时航天器实际姿态Q与期望姿态Qd之间的姿态跟踪误差可定义为Qe=Q-1d⊗Q=［e0eT］T∈R4，其中“⊗”表示四元数乘法.定义角速度跟踪误差为ωe=R3，则有

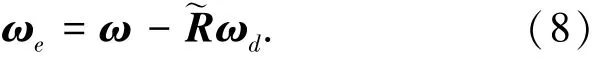
由式（5）～（8）可得出存在执行机构安装偏差的航天器姿态跟踪数学模型为

2 姿态补偿控制器设计

首先设计滑模控制为［8］

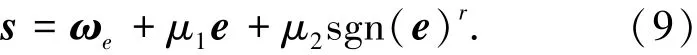
其中μ1、μ2与0＜r＜1均为正常数，sgn（e）r=［｜e1｜rsgn（e1）｜e2｜rsgn（e2）｜e3｜rsgn（e3）］T.

若选取Lyapunov候选函数为

由于对0＜r＜1有不等式恒成立.因此，根据式（9）与文献［8］的引理3.1可得

由于Qe=［-10］T为不稳定姿态平衡点［9］，则当t→∞时由（10）可证明e→0与e0→1.并进一步可得

由此可得

至此根据式（11）可得

显然0.5＜（1+r）／2＜1，故由文献［8］的引理3.3可保证在有限时间tF1内有V1（t）≡0成立.根据V1（t）的定义可进一步证明对于任意的时间t≥tF1，有e（t）≡0、e0（t）≡1与ωe（t）≡0成立.

根据所选取的滑模面（9），考虑常值但不确定的转动惯量J（即J=0），则有

式中‖L‖=≤α0+α1‖ω‖+α2‖ω‖2，且αi（i=0，1，2）为正常数［3］.定义κ≤λmin（DDT），则有如下定理成立.

定理1针对受外部干扰d作用的刚体航天器姿态系统（1）～（3），若反作用飞轮安装偏差ΔD满足不等式ε=｜｜ΔD｜｜＜1，且设计姿态补偿控制器

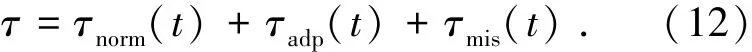
式中

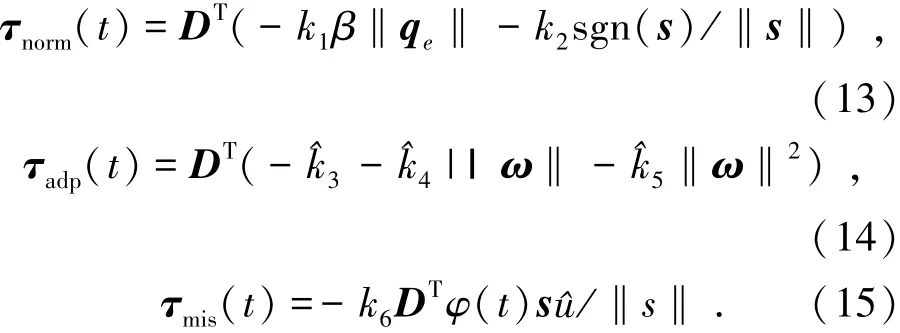
其中sgn（s）=［sgn（s1）sgn（s2）sgn（s3）］T，控制参数k1，k2分别满足k1＞1／κ与k2＞1／κ；、3、4、5分别为u=δ／（κk6）、k3=α0／κ、k4=α1／κ、为k5=α2／κ的估计量，φ（t）=｜｜τnorm+τadp‖∞且φ（t）≥‖τ‖.若设计自适应更新律为=κk6φ（t）‖s‖／l，=κ‖s‖／l3，=κ‖s‖‖ω‖／l4，=κ‖s‖‖ω‖2／l5，其中l1，l3，l4，l5为正常数，则对于任意的初始状态Q（0）、ω（0），系统状态将在有限时间tF2内到达滑模面s（t）=0上，并一直保持在该滑模面上运动.

证明当s≠0时，选取如下的Lyapunov函数：

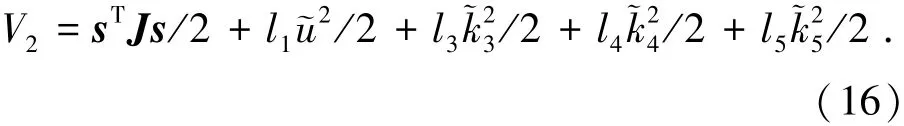
其中，=k3，=k4，=k5式（16）两边同时对时间求导可得

根据式（13）则有

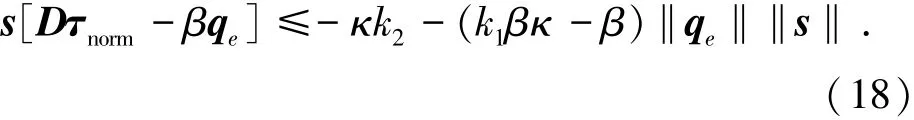
同理根据式（14），则有如下不等式成立：

同理根据式（15）且令‖τ‖≤φ（t），则可得

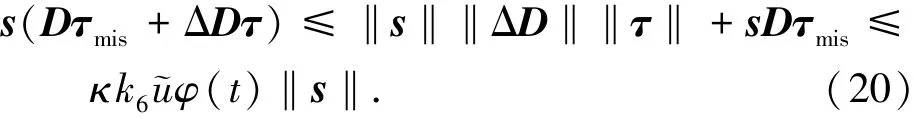
将不等式（18）～（20）代入不等式（17）则有V2≤-（k1βκ-β）‖qe‖‖s‖-κk2≤-κk2，进而有

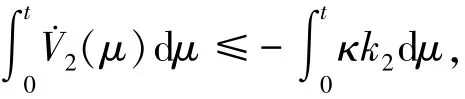
即

由于V2（t）≥0恒成立，因此根据式（21）可证明存在tF2＞V2（0）／（κk2）使得对任意的t≥tF2有V2（t）≡0成立.即在有限时间tF2内，系统状态将到达滑模面s=0上并保持在该滑模面上运动.

证毕.

注2所选取的滑模面（9）是一奇异滑模面，在ei=0（i=1，2，3）处s中的sgn（e）r是连续但不可导的.因此，为了保证因该处不可导而引起控制器（12）产生奇异的情况不发生，控制器（12）的参数以及自适应更新律参数需要小心的选择，确保当s≠0时e≠0得以满足.从而保证在实现（12）时sgn（e）r是可导的，进而避免奇异现象的发生.

根据定理1可确知姿态控制系统状态将在有限时间tF2内到达滑模面s（t）=0上，并一直保持在该滑模面上运动.根据上述分析可知当系统状态到达滑模面（9）时，则在有限时间tF1内系统状态将到达平衡点.因此，对于任意的初始状态Q（0）、ω（0），对t≥tF=tF1+tF2有e（t）≡0、e0（t）≡1与及ωe（t）≡0成立.即当安装偏差满足不等式ε＜1时，在控制器（12）的作用下，将在有限时间tF=tF1+tF2内实现姿态跟踪闭环系统是几乎全局渐近稳定控制.

3 动态控制分配策略

考虑航天器执行机构具有极值约束及速度约束条件：

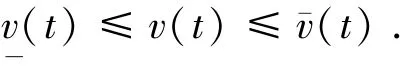
式中v（t）表示控制力矩，且有

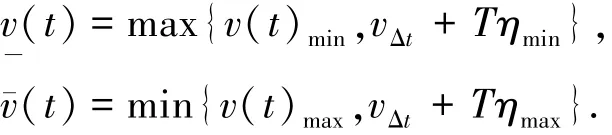
式中ηmin、ηmax分别表示控制力矩变化速度的最小值与最大值，Δt=t-T.进而本文所要实现τ的控制分配问题可描述为

式中W0、W1与W2为相应维数的非奇异权重系数矩阵.

为求解式（22）所描述的优化问题，依据文献［10］中定理1-2，确知动态控制分配问题式（22）的解为

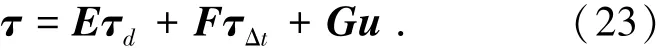
式中：

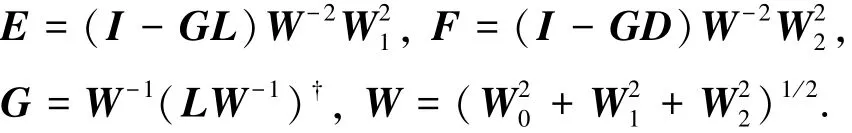
结合式（4）与式（23），可确知本文所采用的动态控制分配策略可以很好的消除误差、抑制干扰，实现理想的控制效果.

4 仿真结果与分析

本文所考虑采用四斜装反作用飞轮控制的航天器，其中3个反作用轮正交安装于航天器本体轴，而在与本体系三轴成等角的方向上安装第4个飞轮.则飞轮实际输出力矩与作用于航天器的总控制力矩之间关系为

设安装偏差角Δαi与Δβi（i=1，2，3，4） 为较小量，

其中：

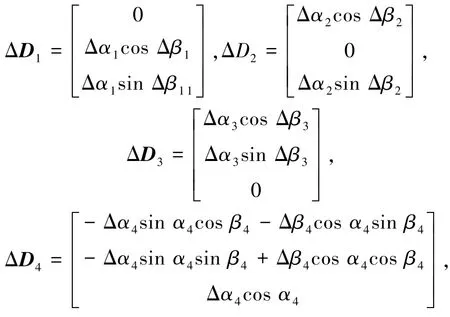
仿真中，Δαi（i=1，2，3）、Δβi（i=1，2，3） 分别在-2°～+2°与-180°～+180°之间随机选择；Δα4、Δβ4在-2°～+2°之间随机选择.航天器外部干扰力矩d（t）采用文献［9］干扰力矩定义.初始角速度以及初始姿态分别为ω（0）=［000］T（rad／s），q（0）=［-0.53-0.260.79］T；期望角速度及期望姿态分别为ωd（t）=0.001sin（2πt）［111］T（rad／s），qd（0）=［000］T.控制器（12）中的控制参数设计为β=0.7，κ=1.05，ki=1.5（i=1，3，41.5（i=1，3，4，5动态控制分配参数设定为：vmin=-0.15 N·m，vmax=0.15 N·m，T=0.2，ηmin=-0.025与ηmax=0.025.航天器标称转动惯量J0与不确定惯量ΔJ分别为

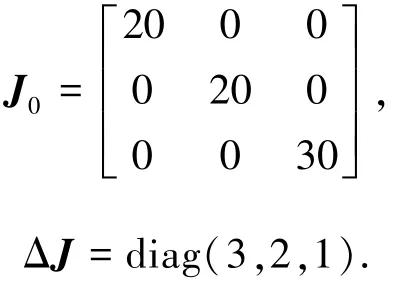
当存在上述反作用飞轮安装偏差、外部干扰、不确定转动惯量时，采用控制器（12）进行姿态跟踪控制，并采用动态控制分配策略（23）进行能量优化控制.

从图1航天器跟踪误差角速度以及姿态跟踪误差的时间响应曲线可知，即使存在大的飞轮安装偏差，文中所设计的控制器可保证星体姿态在30 s内跟踪上期望姿态，实现航天器姿态的高精度稳定控制.图2给出了未加入动态控制分配（NCA）与加入动态控制分配（CA）的力矩输出情况，从图示可知在同时面临外部干扰及安装偏差情况下，本文设计控制器能保证力矩稳定的输出.图3给出了在没有控制分配情况及采用动态控制分配策略两种情况下的能量消耗柱状图，进一步验证了本文所提动态控制分配策略具有较好的实现能源消耗优化的能力.

图1 角速度、姿态跟踪误差时间响应曲线

图2 控制力矩时间响应曲线

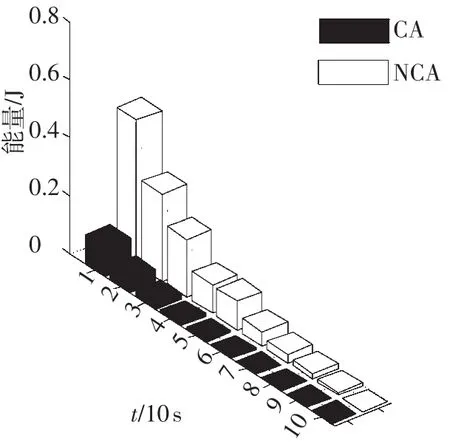
图3 能量消耗对比柱状图

5 结 论

针对存在执行机构安装偏差及外部干扰力矩的过驱动航天器姿态控制问题，本文提出一种姿态控制策略以实现对干扰与安装偏差控制.考虑星载能源消耗的优化、执行机构输出力矩的幅值受限与速率受限等问题，设计了动态控制分配策略实现航天器姿态高精度控制的同时，保证能量消耗最优控制.需要强调的是本文并没有考虑时变的不确定转动惯量，而实际航天工程中由于存在大量柔性机构运动（如太阳帆和天线），因此弹性对测量将产生主要的不确定性影响.为此如何用冗余控制消除弹性对测量造成的不确定性影响将是作者下一步的研究工作.

［1］LI Z X，WANG B L.Robust attitude tracking control of spacecraft in the presence of disturbances［J］.Journal of Guidance Control and Dynamics，2007，30（4）：1156-1159.

［2］YOON H，AGRAWAL B N.Adaptive control of uncertain hamiltonian multi-input multi-output systems：with application to spacecraft control［J］.IEEE Transactions on Control Systems Technology，2009，17（4）：900-906.

［3］CAI W C，LIAO X H，SONG Y D.Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft［J］.Journal of Guidance Control and Dynamics，2008，31（5）：1456-1463.

［4］SANYAL A，FOSBURY A.CHATURVEDI N.Inertiafree spacecraft attitude tracking with disturbance rejection and almost global stabilization［J］.Journal of Guidance Control and Dynamics，2009，32（4）：1167-1178.

［5］TAYEBI A.Unit quaternion-based output feedback for the attitude tracking problem［J］.IEEE Transactions on Automatic Control，2008，53（6）：1516-1520.

［6］SONG Y D，CAI W C.Quaternion observer-based model-independent attitude tracking control of spacecraft［J］.Journal of Guidance Control and Dynamics，2009，32（5）：1476-1482.

［7］LIM H C，BANG H.Adaptive control for satellite formation flying under thrust misalignment［J］.Acta Astronautica，2009，65（1／2）：112-122.

［8］ZHU Z，XIA Y Q，FU M Y.Attitude stabilization of rigid spacecraft with finite-time convergence［J］.International Journal of Robust and Nonlinear Control，2011，21（4）：686-702.

［9］胡庆雷，肖冰，马广富.输入受限的航天器姿态调节小波滑模反步控制 ［J］.哈尔滨工业大学学报，2010，42（5）：678-682.

［10］HARKEGARD O.Dynamic control allocation using constrained quadratic programming［J］.Journal of Guidance，Control and Dynamics，2004，27（2）：1028-1034.