带交易费用和负债的均值-方差投资策略选择

杨 鹏，刘 琦，王献锋

带交易费用和负债的均值-方差投资策略选择

杨 鹏，刘 琦，王献锋*

(西京学院应用理学系, 中国 西安 710123)

研究了均值-方差准则下，带交易费用和负债的投资组合选择问题．研究目标是，在终值财富的均值等于d的限制下，使终值财富的方差最小，即均值-方差组合选择问题．通过使用线性二次控制的理论解决了该问题，获得了最优的投资策略和有效边界的显式解．并通过对所得结果进行进一步分析及实例，在经济上给出了合理的解释．通过本文的研究，可以指导投资者在具有负债时选择恰当的投资策略，使自身获得一定的财富而面临的风险最小．

均值-方差准则; 线性二次控制;交易费用;最优策略;有效边界

自从文献[1]对于单时期均值-方差的有效投资组合开展研究以来，许多学者都研究了该问题．均值-方差问题的目标是，在终值财富的均值给定时使其方差最小．近年来，由于人们对经济问题的持续关注，均值-方差投资组合选择问题已成为数理金融研究的热点问题．文献[2]研究了动态多个时代的均值-方差组合问题, 文献[3]在随机LQ的框架下研究了连续时间均值-方差组合问题，通过随机LQ得到了最优策略和有效边界．文献[4]研究了马尔可夫调制市场上具有资产负债的均值-方差组合问题，获得了最优策略和有效边界．文献[5]研究了基于养老金的最优投资的均值-方差问题，应用随机控制理论求得了最优策略和值函数的显式解.类似的文献[6]也应用随机控制论研究了养老金投资问题.另外，随机控制理论也被广泛用来研究最优投资问题[7-11].

我们知道交易是需要费用的，尤其是频繁交易时，交易费用更大．因此在风险投资时，应考虑交易费用，考虑交易费用才更符合实际情况．文献[12]在保险市场上进行投资时，假设交易时带有交易费用．他们通过使用文献[13]中的结论，使用HJB方程的方法把问题适当转化，得到了最优策略和值函数的显式解．

基于上述文献的工作，本文致力于研究具有交易费用的均值-方差投资组合选择问题．本文考虑交易费用的形式和文献[12]一样，但是得到最优投资策略的方法不再使用HJB方程的方法，而是使用了线性二次控制，这一解决均值-方差组合选择问题的通用方法．另外，在研究中本文还考虑了投资者具有负债，最终得到了最优的投资策略和有效边界的显式解，并通过对所得结果进行进一步分析及实例，在经济上给出了合理的解释．同时分析了负债对最优投资策略和有效边界的影响．通过本文的研究，可以指导投资者在具有负债时选择恰当的投资策略，使自身获得一定的财富而面临的风险最小．

1 模型和均值-方差组合选择问题

1.1 模型

为了使数学上更为严格，假设所有的随机过程和随机变量都定义在完备的概率空间(Ω,F,P)上，并且有一满足通常条件的σ-流{Ft,t≥0}，即Ft右连续且P完备．考虑一个金融市场，由n+1个金融资产组成，其中一个是无风险资产(债券)，时刻t的价格{Bt,t≥0}满足下面的方程

dBt=rBtdt，

其中r>0为无风险利率．n个风险资产(股票)，在时刻t时的价格Si(t)满足下面的随机微分方程

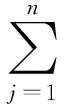
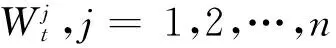
假设投资者在时刻t=0有初始财富x>0与初始负债l(l∈R), 那么投资者在时刻t=0有净初始财富x0=x-l.记Lt为时刻t投资者的累积负债, 假设Lt满足如下的随机微分方程

dLt=Lt[udt+vρdW(t)]，L0=l0>0.

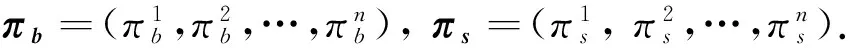
dXt=[rXt+πb(t)B1+πs(t)B2-u]dt+[(πb(t)+πs(t))DT-vρ]dW(t)，

(1)

其中

B1=(r1-r-θb1,…,rn-r-θbn)T,B2=(r1+r-θs1,…,rn+r-θsn)T，D=(σij)n×n．

定义1一个策略π(·)=(πb(·),πs(·))称为可行的，如果π(·)关于流{Ft}是可料的，且对于每个t≥0过程π(·)满足下面的条件

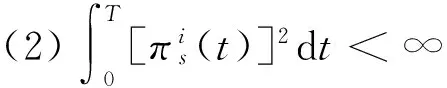
(3) 随机微分方程(1)对于{π(t),t≥0}有唯一的强解，

所有可行的策略记为∏.

1.2 均值-方差组合选择问题

记XT为终值时刻T时投资者的财富，保投资者的目的是，在所有可行策略中找到一个策略π(·)，使得EXT=k，同时使

VarXT=E[XT-EXT]2=E[XT-k]2

最小．该问题称为均值-方差组合选择问题，即如下的描述

定义2均值-方差组合选择问题是以参数k∈R为限制的随机最优化问题，也即

(2)

引理1(2)式定义的均值-方差组合选择问题，对每一个k∈R都是可行的当且仅当ri-r-θbi>0和ri+r-θsi>0，i=1,2,…,n．

证引理的证明和文献[3]相似，因此忽略证明．

有了上述可行性的保证，下面把(2)式定义的均值-方差组合选择问题进行适当的转化．通过应用拉格朗日乘子技巧，上述问题可转化为下面的二次控制问题

J(x0,π(·),λ)=E{[XT-k]2+2λ[XT-k]}=E[XT+λ-k].

因此，目标是求下面无限制的最优化问题

minJ(x0,π(·),λ).

(3)

在下一节里，我们将求解问题(3)．

2 无限制性问题的解

记

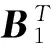
(4)

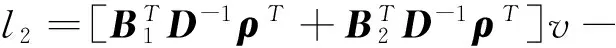
(5)

引理2f(t)满足下面的常微分方程

f′(t)+l1f(t)=0,f(T)=1.

(6)

h(t)满足下面的常微分方程

h′(t)-rh+l2=0,h(T)=0,

(7)

则：

f(t)=el1(T-t),

(8)

(9)

证解常微分方程(6)，(7)即可得到 (8)、(9)．求解过程略．

定理1问题(3)的最优反馈策略为

(10)

(11)

相应的最优值函数为

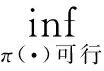
(12)

证令π(·)是任意一个可行的控制策略，并且X(·,π)是(1)的状态轨道．对f(t)[x+(λ-k)e-r(T-t)+h(t)]2应用Ito公式，并应用(6)和(7)，得到

d{f(t)[Xt+(λ-k)e-r(T-t)+h(t)]2}={f′(t)[Xt+(λ-k)e-r(T-t)+h(t)]2+

2f(t)[Xt+(λ-k)e-r(T-t)+h(t)]h′(t)+2f(t)[Xt+(λ-k)e-r(T-t)+h(t)]r(λ-k)e-r(T-t)+

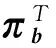
h(t)][(πb(t)+πs(t))DT-vρ]dW(t).

由(8)知f(t)>0．因此，最优反馈策略、最优值函数分别满足(10),(11),(12)．

3 最优策略有和效边界

在这一节中，通过上一节无限制问题的求解，给出(2)定义的均值-方差问题的最优策略和有效边界．

(13)

(14)

有效边界为

(15)

其中λ*满足下式

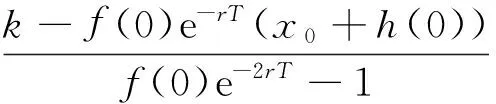
(16)

证根据对偶原理，我们得到

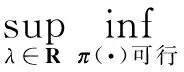
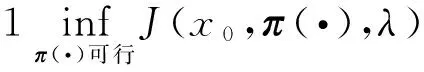
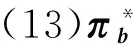
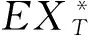
证由式(15)可得到上式．

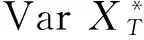
推论3最小最终方差为

(17)

相应的期望终值财富为

(18)

(19)

(20)

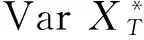
证(15)对k求导数即可得出结论．证明略．

4 数值计算及经济分析

为了解释本文所得结论，本节给出一个数值计算的实例计算上一节得到的最优投资策略和有效边界，并分析负债对最优投资策略和有效边界影响．

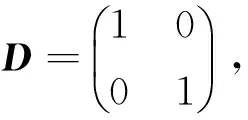
1) 负债的参数v=1，u=0,0.01,0.05,

表1 v=1时最优投资策略和有效边界的取值

表2 u=0.05时最优投资策略和有效边界的取值

[1] MARKOWITZ H M. Portfolio section[J]. J Finance, 1952,7(1):77-91.

[2] LI D, NG W L. Optimal dynamic portfolio selection: multi-period mean-variance formulation[J]. Math Finance, 2000,10(3):387-406.

[3] ZHOU X, YIN G. Markowitz’s mean-variance portfolio selection with rergime switching: A continuous-time model[J]. SIAM J Control Optim, 2003,42(4):1466- 1482

[4] XIE S X. Continuous-time portfolio selection with liability and regime switching[J]. Insurance: Math Econom, 2009,45(1):148-155.

[5] 张初兵，荣喜民. 均值-方差模型下DC型养老金的随机最优控制[J].系统工程理论与实践, 2012,32(6):1314-1323.

[6] 林 祥，杨益非. Heston随机方差模型下确定缴费型养老金的最优投资[J].应用数学, 2010,23(2):413-418.

[7] LIN X, ZHANG C H, SIU T K. Sotchastic differential portfolio games for an insurer in a jump diffusion sisk process[J].Math Methods Oper Res, 2012,75:83-100.

[8] 欧 辉,李代绪,杨向群.债券价格随机时重设型熊市认售权证的定价[J].湖南师范大学自然科学学报, 2011,34(6):16-20.

[9] 周杰明,欧 辉,莫晓云,等.对股东和投保人均分红的带干扰的复合泊松风险模型(英文) [J].湖南师范大学自然科学学报, 2012,35(6):1-13.

[10] 钱艳英.最优投资组合的风险补偿分析[J]. 湘潭大学自然科学学报, 2005,27(3):24-27.

[11] 孟志青,蒋 敏,虞晓芬.基于多目标条件风险值模型的房地产组合投资研究[J].湘潭大学自然科学学报, 2008,30(4):141-148.

[12] ZHANG X L, ZHANG K C, YU X J. Optimal proportional reinsurance and investment with transaction cost maximizing the terminal wealth [J]. Insurance: Math Econom, 2009,44(3):473-478.

[13] SHREVES S, SONER H M. Optimal investment and consumption with transaction costs [J].Ann Appl Probab, 1994,4:609-692.

[14] 杨 鹏,林 祥.带交易费用的最优投资和比例再保险[J].经济数学, 2011,28(2),29-33.

(编辑 胡文杰)

Mean-Variance Portfolio Selection with Transaction Costs and Liability

YANGPeng,LIUQi,WANGXian-feng*

(Department of Applied Science, Xijing University, Xi’an 710123, China)

Investment portfolio selection problem with transaction costs and liability is considered under mean-variance criterion. The main goal is to minimize the variance of the terminal wealth under the constraint that terminal wealth is equivalent tod, namely, the mean-variance portfolio selection problem. Applying linear-quadratic theory, optimal investment strategies as well as the mean-variance valid frontier are then analytically derived. Meanwhile, according to the further analysis and practical example, an explanation in economy is given. This research could be adopted by investors with liability to select the appropriate investment strategy for more wealth while minimizing the risk.

mean-variance criterion; linear-quadratic control; transaction costs; optimal strategies; efficient frontier

2013-03-31

国家自然科学基金资助项目 (11271375)；西京学院校级科研资助项目(XJ130246)

*

,E-mail：yangpeng511@163.com

F830,O211.3

A

1000-2537(2014)06-0073-06