基于Mises屈服条件的外压圆筒自增强研究

唐 峰,朱瑞林,夏新远

(1.湖南师范大学工程与设计学院，中国 长沙 410081；2.中航工业飞机起落架有限责任公司，中国 长沙 410200)

基于Mises屈服条件的外压圆筒自增强研究

唐 峰1*,朱瑞林1,夏新远2

(1.湖南师范大学工程与设计学院，中国 长沙 410081；2.中航工业飞机起落架有限责任公司，中国 长沙 410200)

为了更加准确地确定超应变度，基于米赛斯(Mises)屈服准则，建立了外压圆筒应力方程．在此基础上，按卸载定理分别建立了受外压与受内压圆筒自增强方程，通过对当量应力求解，获得在弹性阶段与塑性阶段产生屈服的规律，并与按屈雷斯加(Tresca)屈服条件导出的方程进行了比较．研究表明，外压圆筒的弹性及塑性应力方程与受内压圆筒状态时方程不同，自增强处理后的残余应力大小也有差异，而且按米赛斯屈服准则的残余应力分量比按屈雷斯加屈服条件的残余应力分量大．但由于内外压圆筒的残余应力的当量应力形式是一样的，所以两个强度理论导出的结果在许多地方相同．

外压圆筒；自增强；弹塑性应力；强度理论

随着外压容器已广泛应用于真空贮罐、减压塔、潜艇外壳等，相应的外压自增强理论的研究也在不断深入．文献[1]按第三强度理论，即屈雷斯加(Tresca)屈服条件导出外压圆筒弹-塑性应力参数方程，即用最大切应力理论较为满意地解释了塑性材料的屈服现象．但不同的材料可能发生不同形式的失效，即使同一材料在不同的应力状态下也可能有不同的失效形式[2]，该理论没有考虑到其它主剪应力的影响．所以，本文基于米赛斯(Mises)屈服条件，即按均方根剪应力理论对圆筒受外压条件下的自增强理论进行了研究，建立了外压圆筒自增强解析解与关系曲线，这对研究外压圆筒自增强有着重要意义．

1 圆筒各向弹-塑性应力计算

设圆筒内、外半径各为ri、ro，所受外压为p，弹-塑性界面半径为rj．为了分析方便，定义k=ro/ri为径比，kj=rj/ri称为塑性区厚度，pj为弹-塑性界面上的压力．

圆筒体一般由钢材料制成，其破坏形式多为塑性屈服，满足米赛斯(Mises)条件，按照第四强度理论，则有[3]

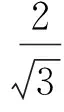
(1)

式中，σr、σt分别为径、周向应力屈服强度．

根据筒壁单元体的平衡方程为：dσr/dr+(σr-σt)/r=0[3]，将式(1)代入该式得：dσr/dr+σs/r=0，则该式的解为：

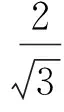
(2)

式(2)的边界条件：(1)r=ri时，σr=0； (2)r=rj时，σr=σpj．

由条件(1)与式(2)联合解出积分常数C，将C代回式(2)得塑性区：

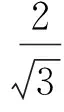
(3)

由式(1)得：

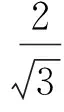
(4)

而轴向应力：

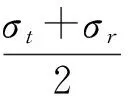
(5)

由条件(2)与式(3) 联合求解，得弹-塑性区界面压力：

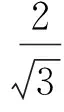
(6)

代入式(1)求解出：

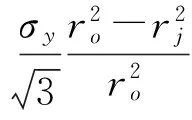
(7)

令式(6)=式(7)得外压与相应的rj的关系：

(8)

该等式的右边第一项表示塑性层全屈服压力大小，第二项表示弹性层内壁面初始屈服压力大小．

在式(8)中，令kj=1得初始屈服载荷：

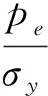
而在弹性区的应力可由文献[3～5]等直接得到：

(9)

(10)

(11)

取k=3.5，kj=1.712 76…(p=1.060 442…σy)和kj=k=3.5(全屈服，p=1.446 566…σy)，得弹-塑性状态应力分布状态，分别如图1(a)、(b)所示．

(a) (b)1. σr/σy; 2.σz/σy; 3. σt/σy

式(8)表示的是进行自增强处理时所需要施加的外压pa大小，即自增强压力，由该式可知，压力与塑性区厚度有关，所以只要rj确定了，自增强压力就可按式(8)求得，并在此基础上，可以对外压自增强进行分析．

2 内外压自增强方程推导及理论的建立

圆筒容器在卸除pa后，筒壁中会存在残余应力大小，按卸载定理[3]推导，分别求得径向、周向、轴向应力改变量：

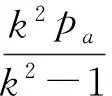
(12)

将式(8)代入式(12)得，应力改变量分别为：

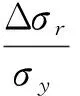
(13)

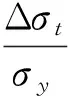
(14)

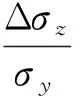
(15)

再将式(3)～(5)和式(9)～(11)与式(13)～(15)相减，求得残余应力．

塑性区：

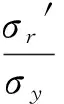
(16)

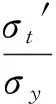
(17)

(18)

弹性区：

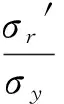
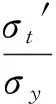
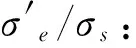
(19)

(20)

尽管由式(19)、(20)公式得出弹-塑性区残余应力的当量应力与按第三强度分析的结果相同[1]，但是由式(16)～(18)所得出的计算结果不相同，这是由于米赛斯(Mises)屈服条件与屈雷斯加( Tresca) 屈服条件之间的条件不同所致，由此可见，虽然两个强度理论都适用于塑性屈服材料，但第三强度理论只适用拉伸屈服极限与压缩屈服极限相同的材料．

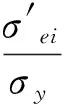
(21)

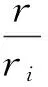
(22)

在式(21)中令kj=k，得全屈服时容器内表面残余应力的当量应力为：

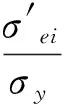
(23)

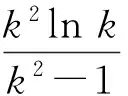
(24)

解式(24)得：

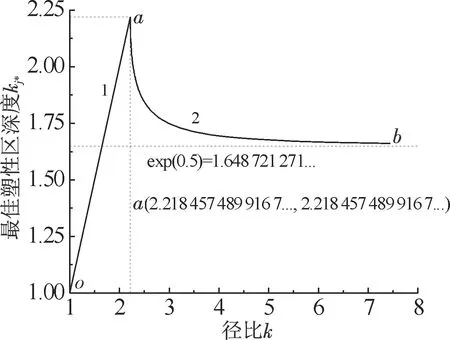
1. kj*=k; 2. k2ln kj*2-k2-kj*2+2=0

k≤2.218 457 489 916 7…=kc,

(25)

令kc=2.218 457 489 916 7…为临界径比．

因此，当k≤kc时，容器不会产生屈服；而k≥kc时，容器会产生屈服．

k2lnkj*2-k2-kj*2+2=0,

(26)

或

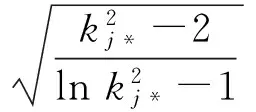
(27)

由以上比较分析可知，式(22)～(27)与外压容器公式相同，并且与按第三强度计算情况相同[1，6-7]．用图表示最佳塑性厚度，如图2(实线oab)所示．

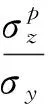
外压引起的当量应力是：

(28)

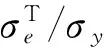
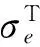
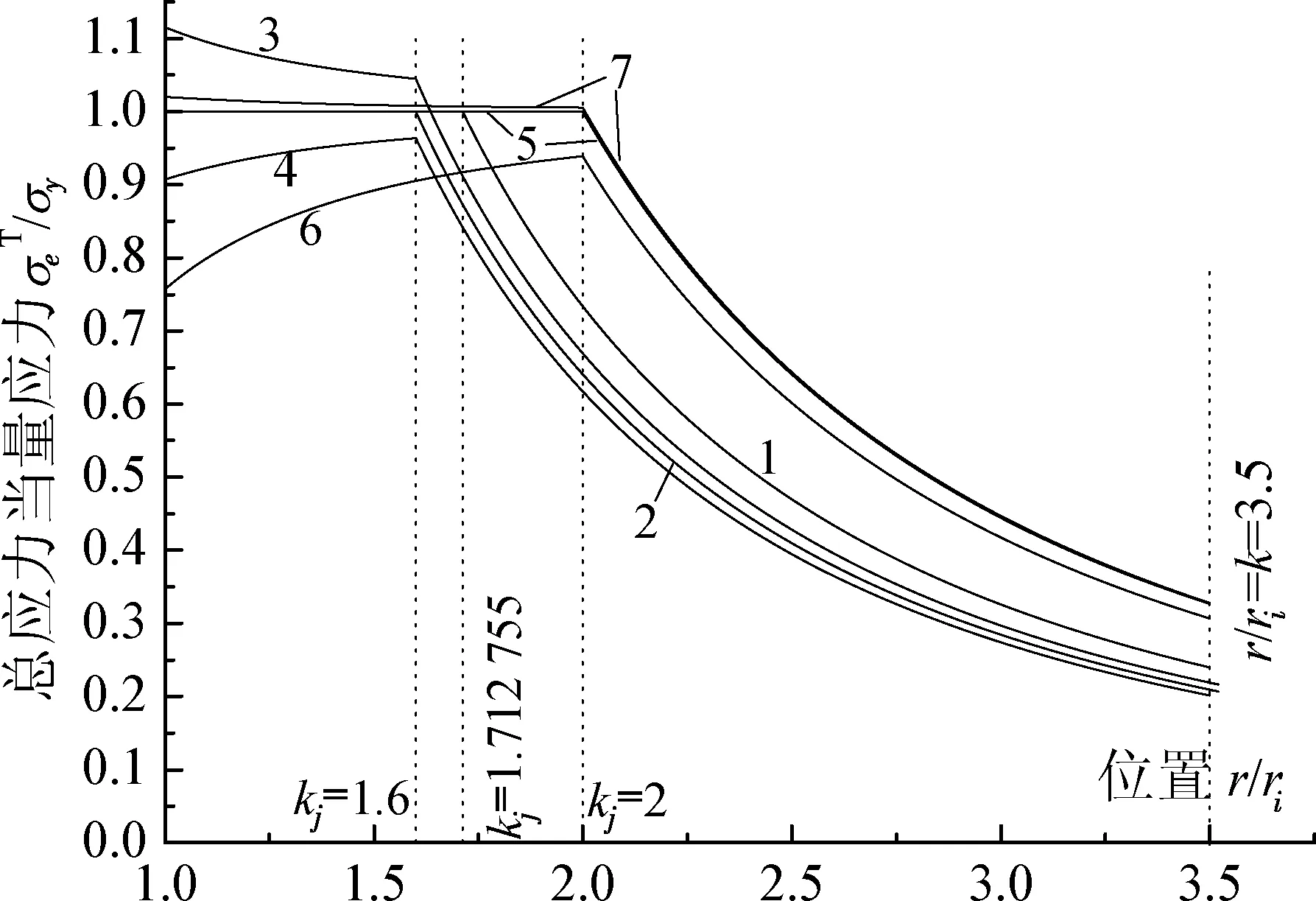
1. k=3.5，kj=1.712 755，p/σy=1.060 439(按式(8)确定);2. k=3.5，kj=1.6，p/σy=0.999 409(按式(8)确定);3. k=3.5，kj=1.6，p/σy=1.060 439(大于式(8)确定的值) ;4. k=3.5，kj=1.6，p/σy=0.95(小于式(8)确定的值);5. k=3.5，kj=2，p/σy=1.189 205(按式(8)确定);6. k=3.5，kj=2，p/σy=1.060 439(小于式(8)确定的值);7. k=3.5，kj=2，p/σy=1.2(大于式(8)确定的值)

由于钢材在外压作用下，会出现弹性与塑性变化情况，因而需要分别讨论．

塑性区内当量应力，由上面讨论可得：

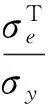
(29)

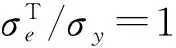
(30)

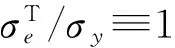
弹性区内当量应力：

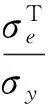
当kj达到k位置时，即kj=k，式(30)成为全屈服压力(py/σy)[1,6-7]：

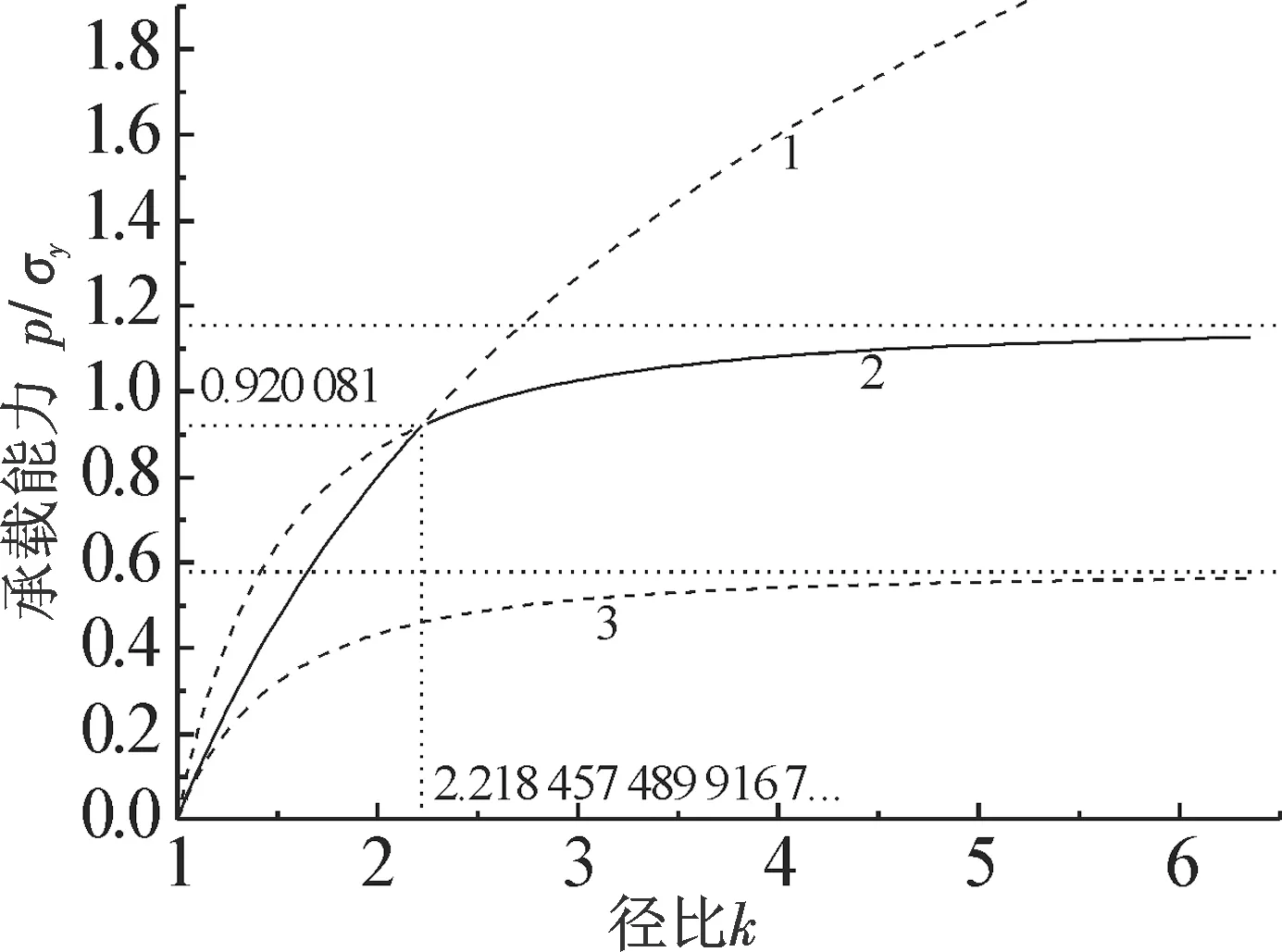
1. py/σy=(2/30.5)ln k; 2. p/σy=2pe/σy; 3. pe/σy

(31)

结合式(30)与(26)可得：当kj=kj*时，自增强容器的承载压力为：

(32)

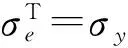
将式(32)代入(29)得：

σep*/σy=2(r/ri)-2,

于是在塑性区当量应力：

(33)

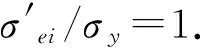
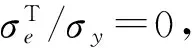
(34)

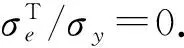
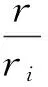
在容器内表面，r/ri=1，于是式(34)成为：

(35)

在容器弹塑性界面处，r/ri=kj，式(34)成为：

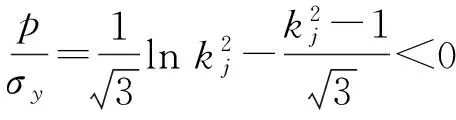
(36)

当kj=kj*时，结合式(36)与(26)可得：

由式(30)/(35)得：

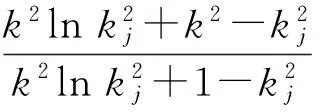
(37)

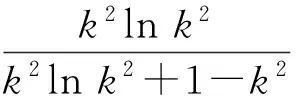
为了求解总当量应力，将式(35)代入式(29)得：

(38)

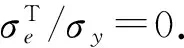
因此，自增强容器承受由式(35)所表达的载荷时，一定不会屈服．

在弹性区当量应力：

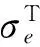
在容器外表面，r/ri=ro/ri=k，则

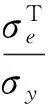
(39)

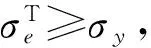
(40)

3 结论

按第四强度理论建立了外压圆筒应力方程，并在此基础上，按卸载定理建立了外压圆筒自增强理论与设计计算方法，通过对该解析解分析，获得产生屈服条件及规律， 这些规律、关系式及数据、图表，可作为圆筒压力容器工程设计时参考的依据．内压自增强圆筒建立过程与外压自增强圆筒相同，所以本文建立的外压圆筒自增强理论同样适用于内压自增强圆筒，其中本文讨论的一些参数可以用于实际生产．

[1] 朱瑞林，朱国林.外压自增强圆筒的设计计算方法[J].中国机械工程， 2010，21(15)：1869-1874.

[2] 刘鸿文. 材料力学[M]. 北京：高等教育出版社， 2008.

[3] 余国琮. 化工容器及设备[M]. 北京：化学工业出版社， 1980.

[4] 陈国理. 压力容器及化工设备[M].广州：华南理工大学出版社， 1994.

[5] 郑津洋，董其伍，桑之富. 过程设备设计 [M].北京：化学工业出版社， 2001.

[6] ZHU R L. Results resulting from autofrettage of cylinder[J]. Chin J Mech Engin, 2008，21(4)：105-110.

[7] ZHU R L. Ultimate load-bearing capacity of cylinder derived from autofrettage under ideal condition[J]. Chin J Mech Engin, 2008，21(5)：80-87.

[8] 《数学手册》编写组. 数学手册[M]. 北京: 高等教育出版社, 1984.

[9] ZHU R L, ZHU G L, TANG F. Anaylysis on autofrettage of clinders[J]. Chin J Mech Engin, 2012，25(3)：615-618.

[10] 贾红光.基于ANSYS的厚壁圆筒的弹塑性应力分析 [J].青海大学学报:自然科学版, 2010，28(3)：8-12.

[11] 唐 峰，许第洪.SolidWorks与Pro/Engineer之间图形数据交换方式的研究[J].湖南师范大学自然科学学报, 2011，34(1):37-42.

[12] 陈盛秒.外层容器设计的公式法及其应用[J].压力容器， 2008，28(1)：30-33.

(编辑 陈笑梅)

Study on Autofrettage of External Pressure Cylinders Based on Mises Yield Criterion

TANGFeng1*,ZHURui-lin1,XIAXin-yuan2

(1. College of Polytechnic, Hunan Normal University, Changsha 410081, China;2. AVIC Landing Gear Advanced Manufacturing Corp, Changsha 410200, China)

In order to accurately determine the value of super strain，the strain equation of pressure cylinders was established on the basis of Mises yield criterion. Based on this，the equation on autofrettage of external pressure cylinders and internal pressure cylinders was built by offloading theorem，the yield rule in the plastic stage and the elastic phase was obtained through solving equivalent stress, and comparison between the results based on Mises and Tresca yield criterion was made. Results show that the elastic and the plastic stresses of the external pressure cylinders are different from equation of the internal pressure cylinders and their residual stresses after removing autofrettage pressure also differ from each other. The components of the residual stresses based on Mises yield criterion are greater than those based on Tresca yield criterion. But the equivalent stress expression of residual stresses of the external pressure cylinders is the same as the internal pressure cylinders. Therefore, the derived results are identical with that according to Tresca yield criterion and Mises yield criterion in many places.

external pressure vessel; autofrettage; elastic-plastic stresses; load-bearing capacity

2013-11-21

国家自然科学基金资助项目(51275060);湖南省科技厅资助项目(2012GK3122);湖南省高等学校科学研究项目(12C0198)

*

,E-mail：ytangfengmm@sina.com

TH49

A

1000-2537(2014)05-0058-07