基于自抗扰技术的火箭炮伺服系统解耦控制

郑 颖，马大为，姚建勇，乐贵高

(南京理工大学 机械工程学院，江苏 南京 210094)

基于自抗扰技术的火箭炮伺服系统解耦控制

郑 颖，马大为，姚建勇，乐贵高

(南京理工大学 机械工程学院，江苏 南京 210094)

火箭炮伺服系统为方位和俯仰两轴耦合的伺服系统。为研究发射时的两轴耦合问题及燃气流冲击强干扰影响，建立了火箭炮伺服系统双轴转台动力矩方程和耦合系统微分方程，采用基于自抗扰技术的解耦控制方法设计了扩张状态观测器及虚拟控制量。通过扩张状态观测器估计系统总扰动并进行实时补偿，通过虚拟控制量得到实际控制量对耦合系统进行控制。仿真结果表明,基于自抗扰技术的解耦控制提高了火箭炮伺服系统跟踪精度，使系统在两轴负载转矩耦合效应和燃气流冲击下有效地抑制了发射平台振动,满足控制性能指标，对火箭炮两轴耦合控制问题具有一定的理论意义和实用价值。

兵器科学与技术；火箭炮；伺服系统；两轴耦合；自抗扰； 解耦控制

火箭炮伺服系统是方位和俯仰两轴耦合的系统，在发射过程中伺服系统受到两轴负载转矩耦合影响，以往火箭炮伺服系统通常只考虑单轴控制，忽略了两轴耦合的特点。因此考虑火箭炮伺服系统作为双输入双输出系统，研究两轴耦合效应是有必要的。对多变量系统采用鲁棒控制[1]的计算量较大。依靠自抗扰控制技术能较好地解决解耦控制，并且计算量不大，鲁棒性好[2]。自抗扰控制方法在多输入多输出系统中得到广泛应用[3-5]，具有较好的控制效果。笔者建立了火箭炮伺服系统方位和俯仰两轴耦合的动力矩方程及双输入双输出系统微分方程。基于自抗扰技术的解耦控制方法采用跟踪微分器、扩张状态观测器和误差反馈得到虚拟控制量，从而对耦合伺服系统进行控制，具有较好的跟踪精度并有效抑制了燃气流冲击影响。

1 火箭炮耦合系统建模

火箭炮两轴耦合系统坐标系关系变换如图1所示。方位轴框架(包括俯仰轴框架)绕其转动轴Oza逆时针转动角度γ，俯仰轴框架绕其转动轴Oyp逆时针旋转角度β。假设方位轴和俯仰轴框架相对于各自的坐标轴系是轴对称的，方位轴框架(含俯仰轴框架)相对于方位轴框架转动轴Oza的转动惯量为

JOza=Jza+Jxpsin2β+Jzpcos2β

(1)

式中：Jxp为俯仰轴框架绕Oxp轴旋转的转动惯量；Jzp为俯仰轴框架绕Ozp轴旋转的转动惯量；Jza为方位轴框架(不包括俯仰轴框架)绕Oza轴旋转的转动惯量。

俯仰轴框架相对于转动轴Oyp的转动惯量为：

JOyp=Jyp

(2)

式中Jyp为俯仰轴框架绕Oyp轴旋转的转动惯量。

方位轴框架转动时的角速度矢量为

(3)

俯仰轴框架角速度为

(4)

刚体的欧拉动力学方程为[6]

(5)

将式(1)～(4)代入式(5)得两轴转矩方程为

(6)

(7)

俯仰轴和方位轴电机电磁转矩方程为

(8)

(9)

式中：KTp、KTa分别为俯仰轴和方位轴电机转矩系数；Rp、Ra分别为两轴电枢电阻；Up、Ua分别为两轴电机电枢端相电压；np、na分别为两轴减速器减速比；Kep、Kea分别为两轴电机电势系数。

两轴运动方程为

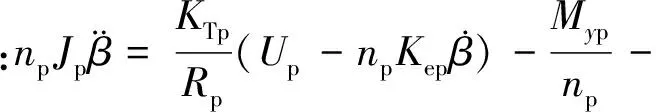
式中：折算到俯仰轴和方位轴电机端的电机及负载转动惯量分别为Jp=9.323×10-3kg·m2，Ja=0.033 kg·m2； 粘滞摩擦系数分别为Bp=1.43×10-4N·m·s/rad，Ba=1.716×10-4N·m·s/rad; 两轴电势系数分别为Kep=0.64 V·s/rad，Kea=0.78 V·s/rad;电枢绕组电阻分别为Rp=2.6 Ω，Ra=1.32 Ω;电机转矩系数分别为KTp=1.11 N·m·A-1，KTa=1.34 N·m·A-1;np=231,na=192;JOza=1 192 kg·m2,JOyp=474 kg·m2。

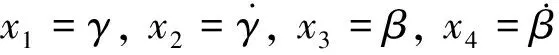
(12)

将各参数数值代入(12)得耦合系统微分方程为

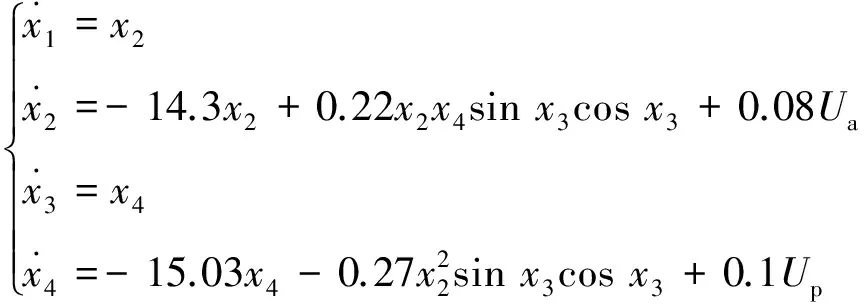
(13)

2 解耦控制

记两轴电机输入相电压虚拟控制量为

(14)

式中,B(t)为耦合系统输入矩阵。

基于自抗扰技术的控制算法为[7]

(15)

(16)

(17)

函数fhan(q1,q2,r,h)定义为

(18)

由式(14)得火箭炮伺服系统两轴实际输入电压值为：

(19)

3 系统仿真

火箭炮耦合系统两轴控制器参数为：r0=500,h=0.01,β1=100,β2=500,β3=3 000,c=1,h1=0.01,r=500。两轴过渡过程初始值均设为0，扩张状态观测器初始值均设为0。

在MATLAB/Simulink中通过S函数建立仿真模型，耦合系统模型为式(13)所示模型，系统输入分别为俯仰和方位两轴实际输入相电压Up和Ua，系统输出分别为火箭炮两轴负载旋转角度β和γ，仿真时间10 s。由式(13)得耦合系统输入矩阵为

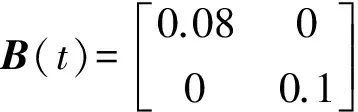
给定火箭炮耦合系统伺服跟踪5 s后每0.5 s间隔发射一次，俯仰轴和方位轴所受燃气流冲击力矩和其他负载扰动如图2所示。

扩张状态观测器对两轴负载旋转角度的估计值和实际输出角度的误差如图3所示。 由图3可得扩张状态观测器能很好估计两轴负载旋转角度值，估计精度较高。

两轴电机输入端电压控制量Up和Ua如图4所示。火箭炮耦合系统两轴输入输出角度误差如图5所示。由图5可得两轴伺服跟踪精度高，跟踪角度误差小于1mrad，满足控制性能指标。在燃气流冲击力矩和负载扰动条件下，耦合系统有效抑制了发射平台振动，使输入输出角度误差限制在1 mrad内，保证了后续射弹精度。

该解耦控制方法和传统PID控制方法对耦合系统的控制误差对比如图6所示。由图6可得火箭炮耦合系统采用传统PID控制输入输出角度误差大于1 mrad，不能满足性能指标。自抗扰控制对耦合系统的控制精度明显高于PID控制，抑制了系统的耦合效应，并有效抑制了燃气流冲击对火箭炮系统的影响。

4 结论

笔者针对火箭炮耦合系统两轴联动时负载耦合的特点，建立了耦合系统的动力矩方程和控制系统耦合微分方程，基于自抗扰控制技术设计了两轴的扩张状态观测器和虚拟控制量从而得到两轴电机输入电压控制量。扩张状态观测器精确估计了两轴负载的旋转角度和系统总扰动，并将总扰动在控制量中予以补偿。同时针对火箭炮伺服系统发射时受燃气流冲击强干扰的特点对耦合系统仿真研究。仿真结果表明,火箭炮耦合系统采用该自抗扰方法在燃气流冲击强干扰条件下具有较好的控制精度，能精确跟踪系统输入指令并有效抑制了负载耦合效应以及燃气流冲击对系统带来的影响。

References)

[1]JAFAROV E M, TASALTIN R. Robust sliding-mode control for the uncertain MIMO Aircraft model F-18[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4): 1127-1141.

[2]HAN Jingqing. From PID to active disturbance rejection control[J]. IEEE Transaction on Industrial Electronics, 2009, 56(3): 900-906.

[3]LIU Bo, XIA Yuanqing, CHEN Jie. Decoupling double loop control system with ADRC[C]∥The 3rd International Conference on Innovative Computing Information and Control.Dalian:[s.n.],2008: 1016-1025.

[4]ZHENG Qing, CHEN Zhongzhou,GAO Zhiqiang. A practical approach to disturbance decoupling control[J]. Control Engineering Practice,2009(17):1016-1025.

[5]XUE Wenchao,HUANG Yi.On performance analysis of ADRC for a class of MIMO lower-triangular nonli-near uncertain systems[J].ISA Transactions,2014,53(4): 955-962.

[6]周长义. 三轴飞行仿真转台控制系统设计与控制算法研究[D].长春：中国科学院长春光学精密机械与物理研究所，2005. ZHOU Changyi. Design control system and study on control algorithm of a three-axis flying-simulating turntable[D].Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2005.(in Chinese)

[7]韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2009:288-292. HAN Jingqing. Active disturbance rejection control technique：the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2009：288-292. (in Chinese)

DecouplingControlofRocketLauncherServoSystemBasedonActiveDisturbanceRejectionTechnique

ZHENG Ying，MA Dawei，YAO Jianyong，LE Guigao

(Mechanical Engineering College, Nanjing University of Science and Technology, Nanjing 210094,Jiangsu, China)

Rocket launcher servo system is a kind of servo system with azimuth axis and pitch axis coupling. For the sake of researching two-axis coupling and strong disturbance of combustion gas flow impact, the two-axis coupling dynamics equations and differential equations of rocket launcher were established. The extended state observer and virtual control variable were designed based on active disturbance rejection control for decoupling. The total disturbance was estimated through extended state observer and system compensation. The real control law was obtained from virtual control variable to control the coupling system. The simulation results indicated that the proposed control method can improve the tracking precision of rocket laun-cher and restrain the vibration of launching platform with two-axis coupling effect and combustion gas flow impact, and the control method can also provide theoretical support and actual value for rocket launcher coupling servo system.

ordnance science and technology； rocket launcher; servo system; two-axis coupling; active disturbance rejection control; decoupling control

2014-06-25；

2014-08-21

国防基础科研项目(B2620110005)；国家自然科学基金(51305203)

郑颖(1984-)，女，博士研究生，主要从事伺服系统控制技术研究。E-mail：zhengyingzky@163.com

TJ393

A

1673-6524(2014)04-0006-05