棕榈叶鞘纤维的拉伸性能

郭 敏，张同华，程 岚，李佳丽

(西南大学 纺织服装学院，重庆 400715)

棕榈叶鞘纤维的拉伸性能

郭 敏，张同华，程 岚，李佳丽

(西南大学 纺织服装学院，重庆 400715)

研究了棕榈叶鞘纤维(棕榈纤维)在4种不同隔距和准静态条件下的拉伸力学行为，应用SEM观察并分析了纤维断裂面的结构，揭示了纤维断裂的机制.结果表明，棕榈纤维的力学指标具有分散性，强度和伸长率随拉伸隔距的增大而变小，而杨氏模量则呈相反趋势.由于棕榈纤维的结构特殊，强度和模量整体呈现随纤维直径增大而变小的特点.在拉伸过程中，微纤丝取向的改变导致了纤维应力应变曲线中的非线性部分变化，断裂面结构展现了受力时4个纤维细胞的变化过程，解释了纤维的断裂机制.

棕榈叶鞘纤维(棕榈纤维)；拉伸强度；微纤丝角；断裂面

天然纤维因其可降解、环保、来源广泛、价格低廉等优势得到了越来越多的关注和研究，尤其是在聚合物基复合材料领域[1-3].棕榈叶鞘纤维(棕榈纤维)在长期的应用过程中，由于其优越的强力、耐腐蚀性和弹性，一直被用于制作农业用绳、雨衣和屋顶材料[4-6].随着天然纤维研究的发展，棕榈纤维的应用范围正逐步扩大，如床垫、弹性材料、复合材料和护坡材料等.本研究在讨论棕榈纤维应力应变曲线和拉伸强力的同时，通过微纤排列变化和断裂面结构揭示了纤维拉伸变形特征.

1 实验

1.1材料

棕皮(图1(a))由云南省红河棕榈协会提供，用自来水浸泡后冲洗掉棕皮在生长过程中附着的杂质，然后在烘箱中干燥.研究所用的棕榈纤维(图1(b))是手工从棕皮中抽取出来的，不进行任何化学处理.从图1(c)，(d)中可以看出，棕榈纤维是天然复合材料，单根纤维(纤维细胞)和导管组织作为增强体，细胞之间的连接物(木质素、果胶和半纤维素)作为基体，其具有与很多天然纤维[7-8]类似的层次结构.其中，单纤维在纵向上相互平行排列，每根单纤维都含有一个中腔.纤维细胞的次生层中含有大量由半纤维素和木质素固着的纤维素微纤丝，其微纤丝角为37.8°～42.2°.

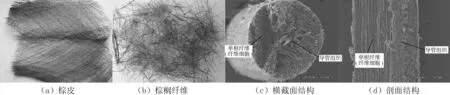
图1 棕榈纤维的结构Fig.1 The structure of palm fiber

1.2纤维的拉伸性能测试

采用标准ASTMD 3379—75中的制样和测试方法对棕榈纤维进行拉伸测试.实验仪器为WDW电子万能试验机，拉伸隔距分别为10 mm，20 mm，30 mm和40 mm，每种隔距测试30个试样，拉伸速度为0.5 mm/min，在此拉伸速度下，棕榈纤维在受力时中体现出准静态拉伸过程[9]，同时利用Zeiss Axioskop 40生物显微镜测量棕榈纤维的直径.

1.3纤维断裂面形貌测试

为了进一步了解纤维的断裂机理，利用S-4800型电子扫描显微镜观察棕榈纤维拉断之后的横截面形貌，测试电压为15 kV.

2 结果与讨论

2.1棕榈纤维的拉伸力学性能

棕榈纤维的典型应力应变曲线如图2(a)所示，该图由3部分组成，对应纤维在拉伸测试时3个不同的变化过程.首先是从0%～1.2%应变的直线部分，其次是从1.2%～13.8%应变的非线性部分，最后是从13.8%应变到纤维发生断裂的线性部分.棕榈纤维在初始受力时，内部的单纤维均受力拉长，应力与应变间呈现线性相关的虎克变形.随着拉伸的进行，纤维发生塑性变形，因为胞壁中微纤丝取向的变化导致纤维内部的非结晶区(主要是半纤维素和木质素部分)的重排.最后，取向排列的微纤丝在持续受力的情况下发生断裂，是对纤维达到一定应变做出的反应.由图2(b)可见，棕榈纤维的拉伸力学行为与亚麻、竹纤维、剑麻纤维以及从棕叶中提取出来的硬质纤维不同，棕榈纤维表现出较低的强力和非常优越的应变拉伸能力，其弹性优势也是用于制作床垫的主要因素之一.

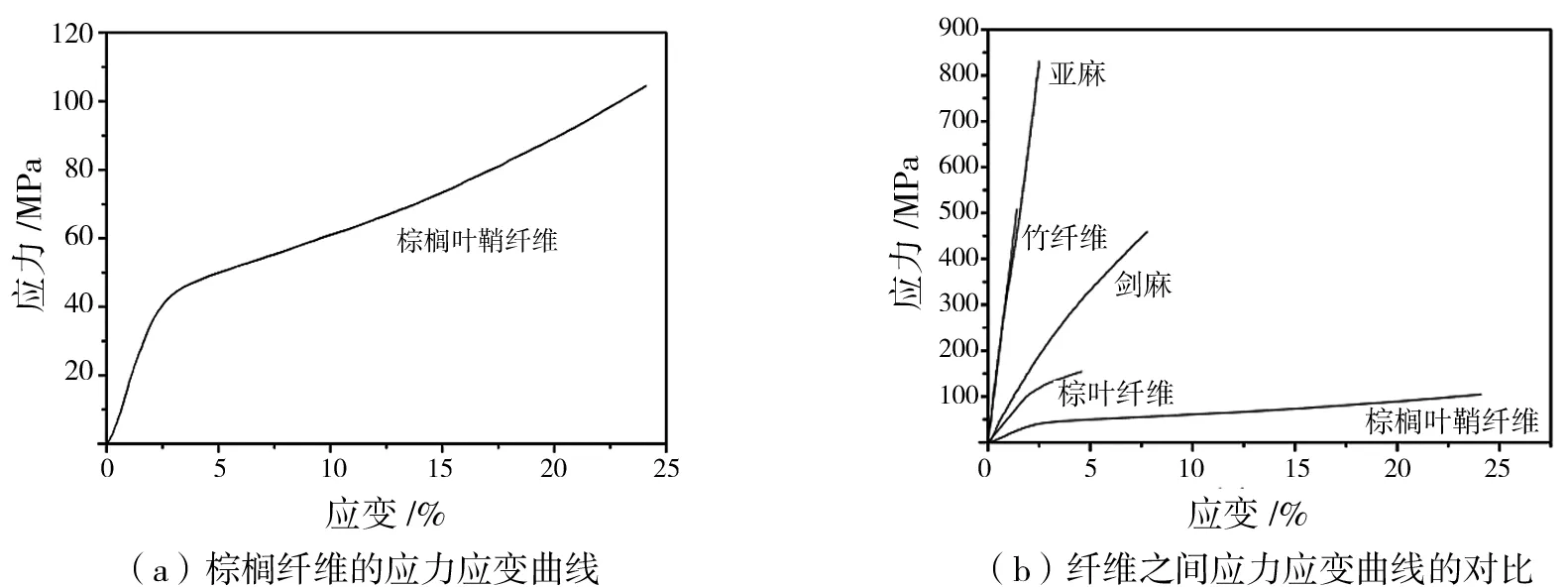
图2 纤维的应力应变曲线Fig.2 The stress-strain curves of fibers

棕榈纤维的拉伸测试结果如表1所示.

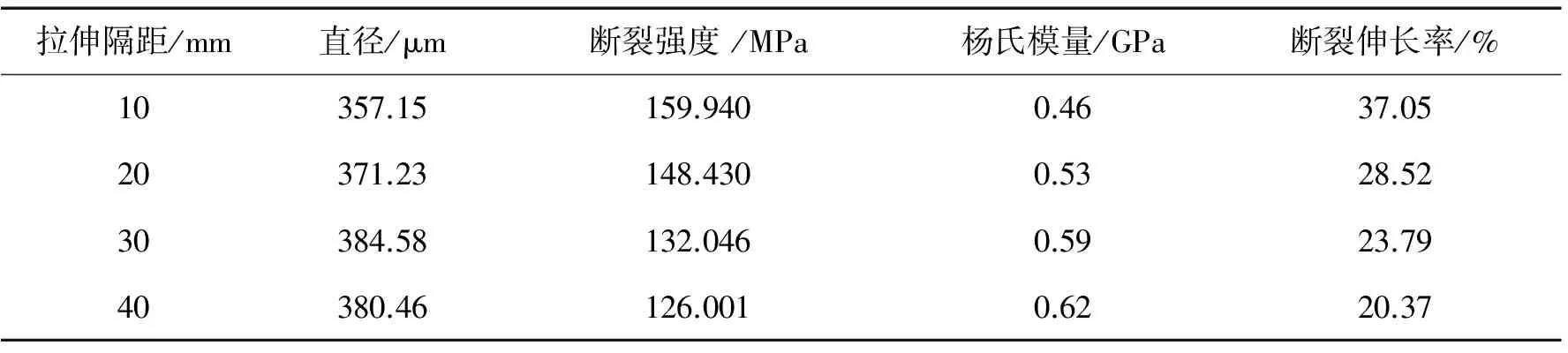
表1 棕榈纤维的拉伸测试结果Tab.1 The tensile test data of palm fiber

由表1可知，棕榈纤维的直径明显大于常用的棉(15～64 μm)、苎麻(30～40 μm)和蚕丝(13～30 μm)等天然纤维，属于一种粗支天然纤维. 纤维的断裂强度和断裂伸长率随着拉伸隔距的增大而变小，杨氏模量则随着隔距的增大而增大，表明棕榈纤维的强度具有一定的分散性且随着隔距的增大强度的分散性亦随之增大，这是天然纤维的典型特征[10-12].因为纤维的断裂首先发生在弱节处，而其在生长过程中，纤维存在各种内部和表面缺陷，测试的长度越长，含有缺陷的概率就越高，纤维就越容易发生形变和断裂，所以纤维的力学性能与拉伸隔距之间有着上述特殊关系.

图3显示了不同拉伸隔距下棕榈纤维的拉伸强度与纤维直径之间的关系.由图3可见，棕榈纤维存在断裂强度和杨氏模量随着纤维直径的增大而变小的整体趋势，Baley[13]也在研究亚麻纤维时表示三者之间类似的关系却没有给出合理的解释.同时，图3揭示了断裂点和纤维平均直径之间没有相关性,纤维的断裂并不是发生在最小直径处(弱节)或者最大直径处，与天然纤维缺陷的随机分布和其所导致的分散性力学性能相一致.

图3 纤维强度和杨氏模量与直径的关系Fig.3 The relationship between strength and diameter of palm fiber

2.2棕榈纤维的拉伸变形

在纤维的拉伸断裂过程中，微纤丝的取向发生变化，给予棕榈纤维特殊的拉伸力学行为.假设棕榈纤维中一根微纤丝的长度为L，与纤维纵轴之间夹角为θ(微纤丝角).纤维在拉伸受力过程中，微纤丝的取向发生变化，并且产生ΔL的伸长量，则可以得到

(1)

图4 棕榈纤维的拉伸微纤丝角Fig.4 The microfibril angles of palm fiber during loading

对应到纤维整体变形中，可以得到

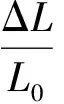
(2)

根据公式(2)计算出纤维变形为13.8%的纤维对应的微纤丝角度θ为29.41°，采用此计算方法得到微纤丝角度分布状况如图4所示.研究表明,通过公式(2)计算得到的这些角度均处在通过XRD测试手段得到的棕榈纤维中微纤丝的角度范围内.同样，利用公式(2)计算通过相同方法进行拉伸测试的亚麻、大麻和苎麻纤维的微纤丝角，也与已有的研究成果一致.

图5 棕榈纤维的拉伸断裂面结构Fig.5 The fracture surfaces of palm fiber

棕榈纤维的拉伸断裂面形貌如图5所示.从图5中可以看出，纤维的断裂由4个不同的纤维细胞变化过程引起，纤维细胞之间因中间连接层在受力拉伸时被破坏而相互分离.图中显示了不同的纤维细胞具有不同的断裂面，且每单个细胞的断裂面也呈现高低不整齐的特点，这是因为每个纤维细胞的随机缺陷分布导致强度的不匀和分散，使得单根纤维在不同的时间不同的平面发生破坏.

3 结论

研究了棕榈纤维的力学行为和断裂机制.棕榈纤维的拉伸力学指标具有非常明显的分散性，强度和伸长率随着隔距的增大而变小，杨氏模量则呈相反的趋势.利用公式计算得到的微纤丝角与实验测试结果相符合.棕榈纤维的断裂面结构显示在纤维拉伸过程中，纤维细胞分离，细胞壁撕裂、剥离和分层，进而引起纤维细胞和纤维整体的断裂.

[1] Obi R K，Sivamohan R G，Uma M C，et al．Structural characterization of coconut tree leaf sheath fiber reinforcement [J]．Journal of Forestry Research，2010，21(1)：53-58．

[2] 王娟，李敏，王绍凯，等．剑麻纤维表面特性及其浸润行为[J]．复合材料学报，2012，29(4)：69-74．

[3] Li Y，Mai Y W，Ye L．Sisal fiber and its composites: a review of recent developments [J]． Composites Science and Technology，2000(60)：2037-2055．

[4] Zhai S C，Li D G，Pan B，et al．Tensile strength of windmill palm (trachycarpus fortunei) fiber bundles and its structural implications [J]．Journal of Materials Science，2012(47)：949-959．

[5] 舒迎澜，陈奕．古代棕榈及其利用[J]．花草撷英，2004(7)：44-45．

[6] 翟胜丞．棕榈类纤维的结构、化学、物理性能[D]．南京：南京林业大学，2010．

[7] Fratzl P，Weinkamer R．Nature’s hierarchical materials [J]．Progress in Materials Science，2007(52)：1263-1334．

[8] Hu K Q．Hierarchical multiscale modeling of statistical strength of fibrous and carbon nanotube composites [D]．New Jersey：Stevens Institute of Technology，2010．

[9] Belaadi A，Bezazi A，Bourchak M，et al．Tensile static and fatigue behaviour of sisal fibers [J]．Materials and Design，2013(46)：76-83．

[10]Andersons J，Porike E S S．The effect of mechanical defects on the strength distribution of elementary flax fibers [J]．Composites Science and Technology，2009(69)：2152-2157．

[11]Charlet K，Eve S，Jernot J P，et al．Tensile deformation of a flax fiber [J]．Procedia Engineering，2009(1)：233-236．

[12]Xia Z P，Yu J Y，Cheng L D，et al．Study on the breaking strength of jute fibers using modified Weibull distribution [J]．Composites，2009(40)：54-59．

[13]Baley C．Analysis of the flax fibers tensile behaviour and analysis of the tensile stiffness increase [J]． Composites，2002(33)：939-948．

Tensilestrengthanddeformationofpalmleafsheathfiber

GUO Min, ZHANG Tong-hua, CHENG Lan, LI Jia-li

(CollegeofTextiles&Garments,SouthwestUniversity,Chongqing400715,China)

In this paper, we investigated the tensile behavior under four different gauge lengths and quasi-static conditions, and the breaking surface was observed and analyzed using SEM in order to reveal the break mechanism. Results show that the mechanical indexes of palm fiber present to be scattered. The strength and elongation decrease, whereas the Young's modulus increases with the increasing of gauge length. According to the special structure, the strength and Young's modulus decrease when the fiber's diameter increases. During the tensile loading, a progressive alignment of the micro-fibrils with the tensile axis provides a quantitative explanation of the nonlinear in stress-strain curve. Additionally, four different processes are illustrated on breaking surfaces instructing the break mechanism of palm fiber.

palm leaf sheath fiber (palm fiber); tensile strength; micro-fibril angle; breaking surface

2013-11-12

中央高校基本科研业务费专项资金资助(XDJK2013A021； XDJK2012D008)

郭敏(1988-)，女，江苏徐州人，硕士研究生，主要研究方向为纤维材料的结构与性能.

张同华(1971-)，男，山东德州人，副教授，博士，主要研究方向为纤维材料的结构与性能.

TS102.1

A

1674-330X(2014)01-0026-04