理想纱条的纤维排列与随机过程分析

严广松，苏玉恒

(1.河南工程学院 理学院，河南 郑州 451191；2. 河南工程学院 纺织学院，河南 郑州 450007)

理想纱条的纤维排列与随机过程分析

严广松1，苏玉恒2

(1.河南工程学院 理学院，河南 郑州 451191；2. 河南工程学院 纺织学院，河南 郑州 450007)

在Rao给出的理想纱条定义的基础上，进一步提出了理想纱条纤维排列的新定义.新定义考虑了纤维的长度分布，从纤维头端排列的概率分布角度指出了理想纱条的形态，新的理想纱条定义完全满足Rao理想纱条的4个条件.使用随机过程对这个新定义的理想纱条进行了分析，证明了这个随机过程是一个弱平稳过程,进一步求出了这个平稳过程的期望、方差和相关函数表达式,为理解理想纱条的意义和拟合非理想纱条建立了理论基础，也给出了理想纱条仿真的数学方法和途径.

理想纱条；纤维排列；纤维头端；随机过程

短纤维纱线一般是指使用具有一定长度分布的天然纤维制造的纤维线性集合体.由于受到纤维长短不一和纺纱加工过程的影响，纤维所形成的纱线会具有一定的均匀度.短纤维纱线的均匀度是重要的纱线质量指标，也一直是纺织基础与应用研究的热点之一,研究短纤维纱线的均匀度对于提高纱线的质量、改进纺纱工艺和研制检测仪器等都具有重要的意义.

纱线的均匀度研究也称为纱线条干不匀研究，这个研究最早起源于20世纪四十年代.Martindale等[1]首先研究了纱线的极限不匀，给出了纱线极限不匀的重要公式，历史上称为Martindale公式.尽管这个公式存在种种缺陷，但是在长期的纺纱工程实践中还是发挥了重要作用.许多学者都对Martindale的纱线不匀理论进行了有益的探索，如Brown, Suh和Zeidman等[2-4]讨论过纱线极限不匀的构成以及概率性质等，取得了一定的进展.近几年来，Yan等[5]研究了纱线截面纤维根数的分布，使用二项分布方法对纱条截面纤维根数进行建模和分析.严广松、苏玉恒[6]建立了平行纤维束头端的一个模型，并且使用Monte Carlo方法对纱线条干均匀度进行了模拟，得到了纱条均匀度的一些性质.为了进一步研究各种纱线中纤维排列的性质，严广松等[7]提出了一种纤维头端的拟均匀分布作为等效分布，对拟合纤维头端的概率分布起到了一定的作用. 匡雪琴、严广松等[8]还提出了极限不匀的一个新数学表达式.

除了研究纱线均匀度的影响因素以及理论分析以外，还有一些关于纱条均匀度的研究集中在理想纱条的研究领域.这个研究最早也是由Martindale提出的，而系统且全面的理想纱条研究则是由Rao完成的[9].

邱燕炜通过对纤维的线密度引入平稳过程和窗函数的概念，对理想纱条的假设进一步减弱，建立了一种更具普遍意义的理想纱条数学模型[10],这也是我国较少见的使用随机过程研究理想纱条的文献之一.

但对理想纱条的研究，迄今为止大部分是基于纱条截面面积的探索，而对纤维在纱线中的排列状态依然缺乏进一步的研究，而且大部分研究都没有考虑纤维的长度分布.如果建立理想纱条中纤维排列的随机规律，而且能够给出理想纱条截面纤维根数变化的随机过程表达，对于随机生成理想纱条进而讨论非理想纱条的随机排列都将是有益的.

本研究假设纤维具有一个长度分布，提出了一个理想纱条纤维排列的分布模型，从而给出了基于纤维随机排列的理想纱条新定义,不仅证明了这个新定义与Rao所给出的定义是一致的，并且进一步分析了这个新定义的理想纱条所形成的截面纤维根数的随机过程,而且证明了这个随机过程是弱平稳的，求出了这个随机过程的期望、方差和相关函数，为今后理想纱条的模拟仿真以及更广泛的讨论打下了基础.

1 理想纱条的新定义

1961年，Rao给出了理想纱条的严格数学定义，按照他的定义，理想纱条是一个满足以下条件的无限长的纤维结构：

(1) 所有纤维顺直且平行于纱线的轴向；

(2) 在纱条的任何一点作为原点，x是离开原点的有向距离，则在区间(x,x+Δx)内恰好出现一个左(右)头端的概率等于μΔx+o(Δx)，其中μ与x无关，o(Δx)是Δx的高阶无穷小；

(3) 单根纤维的线密度均匀不变，不同纤维之间线密度可以不同，但其分布与纤维长度无关；

(4) 各纤维的左(右)头端在轴上的分布相互独立.

Rao在提出上述定义时，强调了纱条形成的前提，也就是任何纺纱过程都无法精确地控制纤维的排列.也就是说，纤维在纱条中只能按照一定概率分布进行排列.上述定义尽管描述了理想纱条的基本结构，但是并没有进一步给出理想纱条中纤维随机排列的规律.如果考虑到纤维的长度分布，而且进一步说明理想纱条的纤维排列，可以将上述定义进一步写成下列新定义：

(1′)所有纤维顺直且平行于纱线的轴向；

(2′)设纤维的长度具有分布密度函数f(x)，最长长度为s，则在纱条上任何长为s区间上，均含有N个纤维的头端,且这些头端在长为s的任何区间内是均匀分布的；

(3′)单根纤维的线密度均匀不变，不同纤维之间线密度可以不同，但其分布与纤维长度无关；

(4′)各纤维的左(右)端头在x轴上的分布相互独立.

这个定义只有第(2′)条与Rao的定义不同，实际上是更进一步指出了理想纱条中纤维的随机排列规律，下面只需证明新定义的第(2′)条满足Rao的第(2)条即可.

按照新定义的均匀分布假设，下面证明在纱条上任取一点，x是离开原点的有向距离，则在区间(x,x+Δx)内恰好出现一个头端的概率等于μΔx+o(Δx)，其中μ与x无关，o(Δx)是Δx的高阶无穷小.

(1)

由于

(2)

代入(1)式，有

(3)

显然，(3)式中的s是一个与Δx无关的量，且(3)式的后一项是Δx的高阶无穷小.这表明，新定义对纤维在纱线中随机排列的描述符合理想纱条的原始定义.

理想纱条的新定义进一步给出了理想纱条中纤维的分布特征，对于具有一定长度分布的纤维，可以按照这个定义来进一步分析.

2 理想纱条纤维的随机排列

2.1理想纱条截面纤维根数的期望与方差

首先要按照理想纱条的新定义，把纤维在纱条中的排列做一个分析.

任何一根纱条截面内的纤维，都是头端在这个截面左侧的纤维向右伸展而形成的.把这个截面记为C-C′，记纤维的最长长度为s，则截面左侧长为s的区段里纤维左头端的个数与纤维长度分布决定着这个截面内纤维根数的分布.

图1 纱条的几何模型Fig.1 The geometric yarn model

图1给出了纤维顺直排列的示意图，其中的C-C′截面是纱条的任一截面.这个截面的横坐标等于纤维的最长长度，这样就能保证这个截面的纤维数是一个典型的纱条.而这个截面的左方，由于纤维都是向右伸展的，所以不是纱条的主体，而是类似于纱线断口的结构.

可以证明，无论纤维长度分布是什么样的，当纤维的左头端在C-C′左侧均匀分布的时候，所得到的C-C′截面上纤维根数的变异系数为最小.

设纤维长度的密度函数是f(x)，纤维的最长长度是s.需要计算通过截面C-C′纤维根数的期望和方差，这个期望与方差就是理想纱条截面纤维根数随机过程的期望与方差.

设纤维的左边头端点为随机变量X，其在0到C-C′截面之间服从均匀分布，其分布密度函数是

(4)

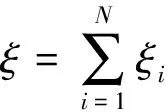
其概率为

P{ξi=1}=p=P{Xi+Yi≥s}，P{ξi=0}=1-p.

(5)

根据二项分布的性质，显然有

(6)

D(ξ)=Np(1-p).

(7)

下面计算P{Xi+Yi≥s}.

带入(6)式和(7)式，有

(8)

从(8)式的结果可以看出，期望与方差都是与随机过程的状态无关的量，于是理想纱条截面纤维根数的随机过程{X(t)}是一个平稳的随机过程.这个随机过程是否为强平稳，取决于它的自相关函数是否与步长有关.

2.2理想纱条截面纤维根数的相关函数

为了能够全面反映理想纱条截面纤维根数随机过程{X(t)}，还需要求出这个随机过程的自相关函数，即R[X(t)X(t+l)].其中,l表示两点间的距离，显然当这个距离大于纤维的最大长度s时，X(t)与X(t+l)无关.

图2 随机过程相邻点之间关系Fig.2 The adjacent points in the stochastic process

按照图1所定义的理想纱条纤维生成过程来求自相关函数显然很难，下面从图2来分析.在图2中，X(t)与X(t+l)相距l，下面来分析计算它们之间的相关函数.

(9)

X(t)和X(t+l)两点上纤维根数的相关系数为

(10)

(10)式的结果显然是合理的，当l变小时，两点之间距离变近，相关系数提高，而当l等于纤维的最大长度s时，相关系数为0.当l=0时，相关系数为1.

按照概率论的知识，相关系数

(11)

所以，

(12)

将(8)式和(10)式的结果代入(12)式，有

(13)

显然，这个随机过程的相关函数是一个与步长有关的量，所以，理想纱条截面纤维根数的随机过程是一个弱平稳的随机过程.

3 结论

在Rao的理想纱条定义基础上，进一步对纱条中纤维的长度分布和纤维头端分布进行了假设，从而给出了与Rao的定义等价的新的理想纱条定义.在使用随机过程对理想纱条截面纤维根数进行分析时，进一步得出，理想纱条截面纤维根数的随机过程是一个弱平稳的过程.根据2.1的分析可以知道，这个弱平稳的随机过程渐进服从正态分布，所以也是个正态过程.

在纤维头端均匀分布假设下，得到了理想纱条截面纤维根数的相关函数，为今后使用随机方法生成纱条的随机过程打下了基础.对理想纱条截面纤维根数的随机过程模拟将采用正态随机过程的性质和Monte Carlo方法进行.对于非理想纱条的建模，还需要在这个基础上进一步研究.

[1] Martindale J G.A new method of measuring the irregularity of yarns with some observations on the origin of irregularities in worsted slivers and yarns[J].Journal of the Textile Institute,1945(36):35-47.

[2] Brown G H,Ly G N. Statistics for the number of fiber ends in a segment of a random assembly of aligned fibers[J].Textile Research Journal,1985,55(4):206-210.

[3] Suh M W.Probabilistic assessment of irregularity in random fiber arrays-effect of fiber length distribution on “variance-length curve”[J].Textile Research Journal,1976(45):291-298.

[4] Zeidman M,Suh M W,Batra S K.A new perspective on yarn unevenness: components and determinants of general unevenness [J].Textile Research Journal,1998,56(4):1-6.

[5] Yan G S,Zhu J Z,Yu C W.A new approach to theoretical yarn unevenness: a binomial distribution model[J]. Journal of the Textile Institute,2010,101(8): 753-757.

[6] 严广松，苏玉恒，朱进忠.纱线条干不匀的随机模拟[J].纺织学报，2012，33(1)：33-37.

[7] 严广松，苏玉恒.棉纱线中纤维头端的等效分布研究[J].河南工程学院学报:自然科学版，2011，23(2)：1-5.

[8] Kuang X,Yan G,Jiang Z, et al.A new mathematical expression of yarn limit unevenness[J].Fibers and Polymers, 2013, 14(11): 1943-1946.

[9] Rao S J.The mathematical model for the ideal sliver and its applications to the theory of roller drafting[J]. Journal of the Textile Institute, 1961(52):570-600.

[10]邱燕炜.理想纱条的数学建模[J].中国纺织大学学报，1999, 25(3): 6-9.

Thealignmentoffibersinidealsliveranditsanalysisbystochasticprocess

YAN Guang-song1, SU Yu-heng2

((1.SchoolofSciences,HenanInstituteofEngineering,Zhengzhou451191,China; 2.CollegeofTextileEngineering,HenanInstituteofEngineering,Zhengzhou450007,China)

Based on the definition of ideal slivers given by Rao, a new definition of ideal slivers concerning the fiber alignment in slivers is proposed. The new definition takes account of the length distribution of the constituent fibers and gives the probability distribution of fiber tips along the length direction of the ideal sliver. The new definition of ideal slivers is proved to be consistent to the four conditions of the former definition given by Rao. A stochastic process analysis is carried out and the result is proved that the stochastic process of the number of fibers in the cross section of the ideal sliver is weakly stationary. And further work is done to have found out the mathematical expectation, the variance and the co-variance of the process. All these works are helpful to the understanding of the ideal sliver and the fitting of the non-ideal slivers. The stochastic process analysis is also a platform of generating ideal silver by simulations.

ideal slivers; fiber alignment; fiber tips; stochastic process

2013-11-18

国家自然科学基金项目(51173023)；河南省高校科技创新团队支持计划项目(13IRTSTHN024)

严广松(1958-)，男，湖北新洲人，教授，博士，主要从事概率与纺纱基础理论研究.

TS101.1

A

1674-330X(2014)01-0001-05