基于AHP的院级科研立项评价研究

周 岩，周 苑

(河南工程学院 计算机学院，河南 郑州 451191)

基于AHP的院级科研立项评价研究

周 岩，周 苑

(河南工程学院 计算机学院，河南 郑州 451191)

从科研项目立项的重要性出发，探讨了层次分析法在立项评价中的应用问题.详细介绍了层次分析法的实施步骤，结合实际建立了一套较科学、公正的项目立项评价模型，最后运用层次分析法确定出评价指标的权重，通过实例测试了立项评价过程的正确性.

科研立项评价；层次分析法；评价模型

无论是评定高校办学实力和科研能力的强弱，还是衡量高校教师个人科研水平的高低，高层次项目的立项都占有举足轻重的地位.但是由于资源有限，很多高校都会限定具有校内项目立项经验之后，才能获得申请高级别项目的资格.而且，很多高层次项目也往往源于校内资助项目.因此，为了在校内项目立项过程中确定优先申报项目，建立一套更高效、更客观的项目立项评价体系变得越来越重要[1].

使用由美国著名运筹学家Saaty提出的层次分析法(Analytic Hierarchy Process，AHP)来尝试构建科研项目立项评价体系，并对学院的两个具有典型性的项目实例进行了评估.

1 AHP方法

AHP是一种定量和定性分析相结合的多目标决策方法[2-3], 能够有效地分析目标准则体系层次间的非序列关系.AHP方法的核心是同一层次的成对比较，在递阶的层次结构下，根据规定的相对标度，充分利用评价者的经验和能力作出相应的判断.先对同一层次有关指标的相对重要性进行两两成对比较，然后按层次从上到下合成对于目标的度量.它是将决策者的思维过程实现数量化，从而解决多目标、多层次、多准则决策问题的方法.运用AHP 解决实际问题，大体可分为建立层次结构模型、构造比较矩阵、计算相对权重并进行一致性检验和计算综合权重4个步骤.

1.1建立递阶层次结构模型

这是 AHP 方法的第一步，也是最重要的一步.首先，对系统进行调查研究，将目标准则体系包含的因素按照属性划分为若干不同的个组，以形成不同层次，如可以分解为目标层、准则层、方案层等.然后，将同一层次的元素视为准则，对下一层次的某些元素起支配作用，同时它又受到上一层次元素的支配，这种至上而下的支配关系形成一个递阶结构.

1.2构造两两比较判断矩阵

判断矩阵是层次分析法的基本内容，它是进行相对重要度计算的重要依据.在递阶层次结构建立后，也就确定了上下层次之间元素的隶属关系.然后，按照层次结构模型，从上到下逐层构造判断矩阵.每一层元素都以相邻上一层次某元素作为评价准则，对本级要素两两比较来确定矩阵中的元素，矩阵形式如式(1)：

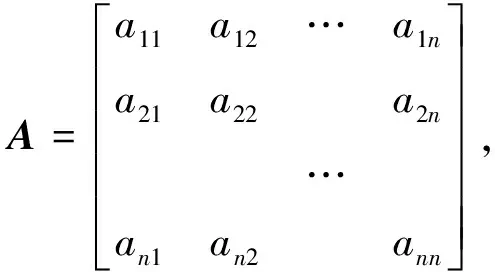
(1)

式(1)中，元素aij的含义为对于评价准则C，元素ai对aj的相对重要性.

判断矩阵的值反映了人们对各元素相对重要性的认识，一般采用1～9比例标度对重要性程度赋值[4]，标度含义如表1所示.

表1 比例标度Tab.1 Ratio scale

1.3计算比较元素的相对权重并进行一致性检验

(1)计算比较元素的相对权重

在进行综合评价时，需要知道下层Ci关于上层C的相对重要度.为此可以求出判断矩阵的最大特征根和对应的特征向量，然后进行归一化处理，即可求出从Ci关于C的相对权重.本研究使用Matlab软件来计算特征值和特征向量w.

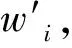
(2)

(2) 进行一致性检验

衡量判断矩阵的标准是矩阵中的元素是否具有一致性.如果某判断矩阵满足如下关系：

aik·akj=aij, 其中i,j,k=1,2,3，…,n,

(3)

则称该判断矩阵具有完全的一致性.但实际情况是，在对评价体系中各元素的重要性进行两两比较时，一般不可能完全精确地判断出wi/wj的比值，只能对它进行估计，所以要求每个判断矩阵具有完全的一致性也是不可能的.因此，为检验层次分析法所得的结果是否合理，需要对判断矩阵进行一致性检验.

第一步，计算矩阵A的最大特征根λmax.为保证决策的一致性，引入了一致性指标

(4)

第二步，查表获得随机一致性指标RI，其中1～10阶判断矩阵的RI值如表2所示.

表2 随机一致性指标Tab.2 Random consistency index

第三步，计算一致性比率CR：

CR=CI/RI,

(5)

若CI和CR均小于0.1，就认为层次单排序值即权重具有一致性，由此计算得到的w值是可以接受的.否则，就要修正检验不合格的判断矩阵, 直到符合满意的一致性标准.

1.4计算组合权重

为了得到递阶层次结构中每一层所有元素相对于总目标的权重，要将上一步的计算结果进行适当组合，并进行一致性检验.这一权重的计算采用从上而下的方法逐层合成.

第k层元素对于总目标的总排序为

(6)

同样，需要对总排序结果进行一致性检验, 若CR(k)<0.1，则认为判断矩阵的整体一致性是可以接受的.

2 实例

2.1建立递阶层次结构模型

建立一套完整的评价指标体系及其评价标准是进行整个评价工作的前提,也是一项复杂的系统工程，必须以先进的评价理论为指导，以科学的设计方法为手段，以现有的对象为基础，以理想的发展目标为导向来构建.在河南工程学院科研项目立项评价指标体系构建的过程中，总结了专家的意见，综合判断后，通过对系统构成因素的深入分析将总体目标逐层分解，划分成若干子目标，最后形成一个由4大类指标构成的树形结构的评价指标体系,共分3层,目标层C、准则层Ci和指标层Cij,如图1所示.

图1 项目立项评价模型Fig.1 Evaluation model of scientific research project

2.2构造两两比较判断矩阵、计算权重并进行一致性检验

对科研项目立项评价系统各指标权重的确定采用图1的评价结构模型，并采用专家咨询的方法来确定评判矩阵.式(7)是专家给出的判断矩阵，按照式(2)计算权重并进行一致性检验.结果如下：

(7)

权重w=(0.096 0.277 0.161 0.466),CI=0.009，CR=0.01<0.1，则矩阵C-Ci具有满意的一致性.

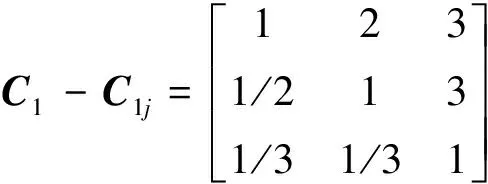
(8)

权重w=(0.525 0.334 0.141 0.466),CI=0.028,CR=0.0481<0.1，则矩阵C1-C1j具有满意的一致性.

(9)

权重w=(0.459 0.226 0.171 0.144),CI=0.014,CR=0.016<0.1，则矩阵C2-C2j具有满意的一致性.

(10)

权重w=(0.500 0.250 0.250),CI=0 <0.1，则矩阵C3-C3j具有满意的一致性.

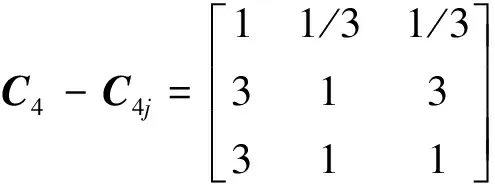
(11)

权重w=(0.143 0.429 0.250),CI=0 <0.1，则矩阵C4-C4j具有满意的一致性.

2.3层次总排序

表3 指标层总权重及排序Tab.3 The total priority of index layer and sorting

利用上一层层次单排序的结果，以上层元素的组合权重为权数，计算对应于本层各元素的加权和，计算结果即为该层元素针对目标层(最上层)的组合权重，进行层次总排序.经计算得出待评目标C各指标的组合权重如表3所示.

接着，计算组合的一致性，即CI=0.005 9,RI=0.254 6,CR=0.023 1<0.1.由此可知，总排序的结果具有满意的一致性，并接受该分析结果.

同理，可以计算出项目D1和项目D2相对立项评价指标C的组合权重.

最后，利用相同的方法计算出项目D1的权重为0.549 1，项目D2的权重为0.449 1，CR= 0.000 0.可以看出，总排序的一致性比率CR<0.1，认为判断矩阵的整体一致性是可以接受的,并且项目D1整体优于项目D2.

3 结论

应用层次分析法构建了项目立项评价模型，并对具有代表性的两个项目实例进行了立项评估.研究结果认为，学院项目申请中比较看重科研实力和应用前景，更注重科研成果的实用性，从而为项目成功申报提供了参考.

[1] 宋云雪,金东瑾,史永胜.基于层次分析法和聚类相结合的科研立项评估系统模型[J].科技管理研究,2009(5)：511-518.

[2] Roussinov D,Chen H.A scalable self-organizing map algorithm for textual classification:a neural network approach to automatic thesaurus generation [J].Communication and Cognition in Artificial Intelligence Journal,1998,15(1/2):81-111.

[3] Saaty T Y .Decision making-the analytic hierarchy and network processes (AHP/ANP)[J].Journal of Systems Science and Systems Engineering,2004(3)：1-35.

[4] Tha J H,Carr V.A proposal for construction project risk assessment using fuzzy logic[J].Construction Management and Economics,2000(18)：491-500.

EvaluationofscientificresearchprojectinregularHEIsbasedonAHP

ZHOU Yan, ZHOU Yuan

(CollegeofComputers,HenanInstituteofEngineering,Zhengzhou451191,China)

Through the importance of the research, the application of AHP in the evaluation of the project is discussed. The AHP method is introduced in detail and a suit of scientific and candid appraisable model is established on the basis of practical case studies. Finally, to compute the weights of the appraisable model are computed using AHP consultation. Real examples are used to verify the correctness of the evaluation process of the project.

evaluation of scientific research project; analytic hierarchy process; evaluation model

2013-12-01

周岩(1981-)，女，河南开封人，讲师，主要研究方向为计算机应用与软件工程.

TP311

A

1674-330X(2014)01-0071-05