La,Ce,Nd掺杂对单层MoS2电子结构的影响∗

雷天民 吴胜宝 张玉明 郭辉 陈德林 张志勇

1)(西安电子科技大学先进材料与纳米科技学院,西安 710071)

2)(西安电子科技大学微电子学院,西安 710071)

3)(西北大学信息科学与技术学院,西安 710069)

1 引 言

随着半导体理论和器件制作工艺技术的不断进步,硅基器件和集成电路的性能愈来愈接近由其材料特性所决定的理论极限,微电子技术的可持续发展迫切需要寻找能替代Si的新型材料.与此同时,石墨烯因其具有独特二维结构和优良电子学特性广受研究者的青睐,成为近十年来全球相关领域的研究热点之一[1−5].然而,本征石墨烯固有的“零带隙”特点对其在半导体器件和集成电路中应用的限制,促使人们把目光转向如MoS2等与石墨烯具有类似层状结构的过渡金属硫族化合物.与石墨烯不同,MoS2本身就是一种天然的半导体[6−8],而且当其由体材料减薄到单层,它的禁带宽度会由1.29 eV增加到1.80 eV,能带结构也由间接带隙转变为直接带隙,意味着单层MoS2材料不仅适合于制作微电子器件,也适合被用来制作光电子器件[9−11]. 因此,国际上已有多个研究小组采用微机械剥离[12]、液相剥离[13,14]和化学气相沉积[15]等方法进行了单层MoS2制备和器件应用研究.研究表明,单层MoS2晶体管室温下的载流子迁移率为200 cm2·V−1·s−1, 电流开关比达到1×108,并且具有超低的待机功耗[16−19],基于MoS2光电探测器[20]以及异质结构[21]研究都说明MoS2具有优良的光电特性,在微电子及光电子器件应用方面具有潜在的应用前景.最近,Zheng等[22]通过使用萘基钠的两步扩张插入方法成功制备出面积达400µm2的高质量单层MoS2;Dankert等[23]在Co和MoS2之间引入薄层TiO2遂道势垒实现了开态电流和迁移率的成倍提升,表明了实现MoS2自旋器件的可能性.同时,运用玻尔兹曼输运理论对不同相MoS2载流子迁移率、稳定相的确定及不同相形成的特殊条件的研究也有报道[24,25].

掺杂是半导体器件或集成电路工艺中最重要的工艺环节之一,通过杂质种类的筛选和掺杂水平的调节,实现半导体光电特性的可控.作为一种新型半导体材料,有关单层MoS2过渡金属掺杂的理论研究已有少量报道,如Tiwari等[26]采用从头算法计算了Fe掺杂MoX2(X=S,Se,Te)的电子结构,发现Fe掺杂对MoX2的电子结构及费米能级附近的能量状态都有影响.吴木生等[27]采用第一性原理研究了Cr和W掺杂对单层MoS2电子结构的影响,发现W掺杂对MoS2的能带结构几乎没有影响,但Cr掺杂则影响很大.曹娟等[28]对V,Cr,Mn掺杂的单层MoS2的磁性进行了计算,发现不同过渡金属掺杂会导致MoS2具有不同的磁表现.众所周知,稀土原子因其存在未充满的4f和5d电子组态、具有丰富的电子能级和长寿命激发态,已经成为ZnO,GaN等宽禁带半导体掺杂体系研究的新热点之一[29−31].但迄今为止尚未发现有关MoS2稀土掺杂的研究报道.本文基于密度泛函理论[32,33]框架下的第一性原理,采用平面波赝势方法对La,Ce和Nd掺杂MoS2的电子结构进行了计算,研究了稀土掺杂对单层MoS2晶体结构和能带结构带来的影响.

2 计算模型与方法

MoS2具有典型的层状结构特点,S原子和Mo原子各自以六边形对称排列,按照S-Mo-S构成三明治结构,每个分子层的层厚为6.5 Å.分子层内原子以共价键结合,层间原子则靠范德华力结合.文中计算所用的MoS26×6×1超晶胞由36个Mo原子和72个S原子构成,通过沿MoS2单胞基矢方向分别扩展6个单位得到.为了不考虑分子层间相互作用,我们把层间真空层设定为18.41 Å.由于主体原子Mo和S的电子组态为[Kr]4d55s1和[Ne]3s23p4,而La,Ce,Nd的电子组态分别为[Xe]5d16s2,[Xe]4f15d16s2,[Xe]4f45d06s2,考虑到稀土原子与主体原子的属性差异以及所建模型的对称性,我们用一个稀土原子替换单层MoS2中一个Mo原子来实现替位式掺杂.所建超胞模型的俯视图及侧视图如图1(a)所示,其中,虚线S-S′,Mo-Mo′代表对差分电荷密度分析时所取的切割面位置.图1(b),(c),(d)分别为La,Ce,Nd掺杂MoS2超胞几何优化后杂质原子附近的晶格变化情况.

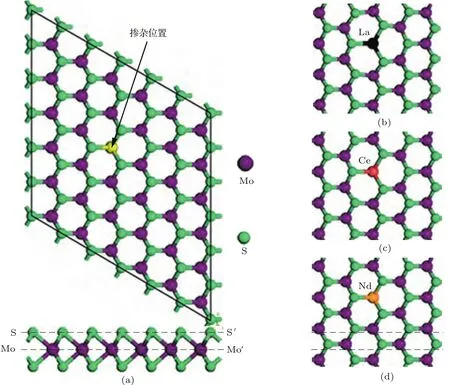
图1 超胞模型及几何结构优化后杂质原子附近晶格变化情况 (a)稀土掺杂MoS2超胞的俯视图和侧视图;(b)La掺杂;(c)Ce掺杂;(d)Nd掺杂

本文计算通过基于密度泛函理论(DFT)的量子力学程序CASTEP来完成.采用平面波赝势法将多电子体系用平面波函数展开,用超软赝势描述离子实与价电子之间的相互作用,电子与电子相互作用交换和相关势由广义梯度近似(GGA)矫正[34].选取的平面波截断能为410 eV,布里渊区能量和电荷密度积分采用倒空间k网格点来处理.同时,采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)方案[35]对稀土掺杂MoS2超胞进行几何结构优化.优化要求原子间作用力不大于0.01 eV/Å,原子的最大位移不大于5.0×10−4Å,能量收敛精度不大于5.0×10−6eV/atom,晶体的内应力不大于0.02 GPa.优化完成后4个参数均达到或优于收敛精度标准.

3 结果与讨论

3.1 La,Ce,Nd杂质附近的晶格畸变

表1给出了本征及稀土掺杂MoS2超胞几何结构优化后的计算结果.其中,dX−S代表X(X=Mo,La,Ce,Nd)原子与其最近邻S原子的键长,dX−Mo代表X 原子与其最近邻Mo原子的距离,dS−S代表离X原子最近的两个S原子之间距离,rX代表X 原子的共价半径,θS−X−S代表X原子与同一S原子面内两个S原子所成的键角.

由表1可以看出,本征MoS2中Mo原子层中的dMo−Mo和S原子层中的dS−S均为3.166 Å,S—Mo键长为2.406 Å,S—Mo—S键角为82.28◦,这些结果与文献[27,36]的计算结果一致.通过表1中的数据对比可以发现,与本征MoS2的晶格参数相比,三种稀土杂质的引入都会导致杂质原子附近的晶格发生畸变,但畸变程度差异较大.就文中所考量的三种杂质而言,La杂质附近的键长变化最大,Nd杂质附近的键长变化最小.当用一个La原子替代单层MoS2中一个Mo原子后,dLa−S和dLa−Mo较之于本征态的相对变化量分别为14.2%和5.6%,dS−S和S—La—S键角的相对变化量甚至高达22.3%和7.7%.我们认为,杂质原子附近的晶格畸变主要源于杂质原子与被替代原子的共价半径不同.由于Ce原子和Nd原子与Mo原子的共价半径之差为0.35 Å和0.34 Å,都小于La与Mo原子的共价半径之差 (0.39 Å),所以其晶格畸变程度略低.其中,Nd原子因其具有最小的共价半径,dNd−S和S—Nd—S键角的相对变化量仅为6.3%和0.3%,远远小于La,Ce掺杂的相应结果.

表1 本征和掺杂MoS2体系优化后的结构参数,X=Mo,La,Ce,Nd

3.2 La,Ce,Nd掺杂MoS2体系的能带结构及态密度

图2为计算所得本征及La,Ce,Nd掺杂MoS2的能带结构,为便于对比分析,能带结构图中的能量统一选取为包含费米能级 (0 eV)在内的−1.0—3.0 eV范围.

从图2可以看出,单层本征MoS2具有直接带隙能带结构,导带底和价带顶都位于布里渊区的K点,禁带宽度约为1.73 eV,且禁带中并无其他能级出现.与本征MoS2相比,La,Ce,Nd掺杂体系的能带结构仍然呈现出直接带隙特点,但与本征MoS2最大的区别是导带底和价带顶都位于G点 (布里渊区中心)而非K点.另外可以发现,除了Nd掺杂体系导带底和价带顶的能量值与本征MoS2相比没有变化之外,La,Ce掺杂体系中两者的能量值都有不同程度的降低,尤其是La掺杂,导带底和价带顶的能量值降低了约0.25—0.45 eV.考虑到La,Ce两个原子的电子组态中都存在d态电子,而Nd的d态电子为零,上述能量值的下降是否与Jahn-Teller效应有关,有待更进一步研究.除此之外,La,Ce,Nd掺杂体系的共同特点是导带的能量状态主要集中在低能量区域,高能量区域的能量状态全部消失,呈现出明显的局域化特点.而且,导带及价带的能级明显比本征态多出许多,这与稀土杂质具有丰富的电子能级特点相符合.

从图2还可以看出,La,Ce,Nd掺杂体系禁带区域的能量状态与本征MoS2完全不同,都出现了数目不等的新能级.La掺杂的禁带中有3个能级,分别位于费米能级以下0.151 eV、费米能级以上0.189 eV和1.276 eV处;Ce掺杂的禁带中有多达6个能级,其中4条主要集中在1.0—1.337 eV的能量范围内;Nd掺杂的四个能级较为集中,主要分布在0.456—0.678 eV能量范围.若从杂质原子最外层的价电子数考虑,由于La原子最外层的价电子数比Mo少3个,禁带中的3个能级恰好对应于La原子依次得到3个电子达到与S原子成键状态的受主能级;Ce原子最外层有4个价电子,其中f,d轨道都只因存在1个电子而未饱和.所以,Ce掺杂MoS2禁带中的6个能级中可能有2条属于施主能级,有4条属于受主能级;Nd的电子组态为[Xe]4f45d06s2,相应禁带中的4个能级属于施主能级的可能性较大,其中亦有可能存在两条受主能级.当然,上述有关杂质能级的讨论,只是我们初步的理论分析,这些能级的具体属性,最终还需通过实验来确认.

图2 本征单层MoS2及掺杂MoS2的能带结构

图3给出了单层本征及稀土掺杂MoS2的总态密度和分态密度按照能量分布的计算结果.其中,图3(a)对应于本征态,选取的能量范围从−19 eV到5.2 eV之间,包含了导带和上、下价带的分布信息.图3(b),(c),(d)分别对应于La,Ce,Nd掺杂MoS2的计算结果,由于3种掺杂体系在高于3.0 eV的能量区域几乎不存在能量状态,为了便于分析,针对3种掺杂体系的能量范围统一选取为−19—3.0 eV.从图3(a)可以看出,掺杂MoS2与本征MoS2导带态密度分布相差较大.本征MoS2导带较宽,其能量分布范围在1.75 eV到12.0 eV之间,且在2.54 eV和9.82 eV能量附近都有较高的能态密度,分波态密度的计算结果说明本征MoS2高能量区域的能量状态主要由S 3s和Mo 5s,Mo 4p电子所贡献.而La,Ce,Nd掺杂体系的导带能量分布范围集中在1.0—3.0 eV,高能量区域原有能量状态的消失有可能是稀土原子与其最近邻S原子按照spd杂化成键而对部分s轨道电子带来限制造成.从图3中3种掺杂体系的总态密度和分态密度分布可以看出,上价带的能量状态主要为S 3p和Mo 4d电子所贡献,下价带的能量状态主要由S 3p和Mo 4d电子所贡献,而导带部分的能量状态仍以S 3p和Mo 4d电子贡献为主,同时也存在杂质原子最外层5d和4f电子贡献,尤其是对于Ce和Nd掺杂,4f电子贡献非常明显,且其态密度的主峰位置都位于禁带当中,与前述能带结构分析吻合.此外,从图3还可以看出,La,Ce,Nd三种原子的5p电子对掺杂体系的能量状态也有贡献,其态密度主峰位置分别位于−15.7 eV,−17.2 eV和−17.6 eV能量位置,相应能级远离费米能级,通常条件下不会对MoS2的光电性能带来影响.需要特别说明的是,Nd从电子组态来看本无d态电子,但当我们对Nd掺杂MoS2超胞采用BFGS方案进行几何优化后发现Nd原子的电子状态中有d态电子出现.由此可以推断,在杂质Nd替代Mo原子与S原子杂化成键过程中,Nd 6s电子跃迁成为5d电子后再与S 3p轨道电子杂化有可能降低体系的总能量,使掺杂体系更加稳定.

图3 (网刊彩色)本征及稀土元素掺杂单层MoS2的态密度 (a)本征MoS2;(b)La掺杂;(c)Ce掺杂;(d)Nd掺杂

3.3 La,Ce,Nd掺杂MoS2的差分电荷密度

为了研究稀土掺杂对MoS2电子分布的影响,更直观地显示因杂质掺入所引起电荷重新分布的物理图像,图4给出了本征MoS2和La,Ce,Nd掺杂MoS2中成键原子与自由原子的差分电荷密度分布.其中,上面4幅图是以Mo原子中心为切割面,下面4幅图是以顶层S原子中心为切割面,图片右侧给出了相应的灰度标尺.

从图4本征MoS2的差分电荷密度图可以看出,所有Mo或S同种原子周围的差分电荷密度分布都相同,但由于二者成键导致Mo或S原子周围的差分电荷密度分布不一样.对于Mo原子切割面,在三个Mo—S键的夹角区域出现3个严格对称的灰色小斑点,其余大部分都为黑色区域,并在Mo—S成键方向上有所延伸,黑色区域对应的差分电荷密度为负值,意味着电子损失;与Mo原子切割面相比,S原子切割面的情况正好相反.S原子周围尤其是在Mo—S成键方向上以白灰色为主要标志,意味着电子聚集.分析认为,本征MoS2中Mo原子的电负性为2.16,S原子的电负性为2.58,由于电负性的大小不同,导致Mo原子易失去电子、S原子易得到电子,故而形成图4所给出的物理图像.

与本征MoS2的差分电荷密度分布相比,La,Ce,Nd掺杂MoS2显示出不同的结果.从Mo原子切割面所显示差分电荷密度图可以看出,La周围大部分呈现出暗灰色区域,其灰度明显低于Mo原子周围的情况,而且也存在较大且层次不同的3个白灰色小斑,这些斑点距三角形中心更远.与Mo原子完全不同的是La原子所在处的中心区域呈现出白色圆斑,意味着该区域电子聚集,与La掺杂MoS2可能存在3条受主能级的前述分析一致.值得注意的是,Ce和Nd掺杂的情况与La掺杂不同,其中心区域类似于Mo原子都为黑色但差分电荷密度分布不同,尤其是Nd原子周围形成了黑白分明、反差极大的不同区域,意味着既有电荷损失,也存在电荷聚集,这点与前述所得的相应杂质能级中有可能出现施主能级和受主能级共存的结论相吻合.结合f态电子和s态电子具有完全不同的波函数分布,我们认为黑白分明的差分电荷密度分布可能与f轨道电子的存在有关.

图4 本征MoS2和掺杂原子附近的差分电荷密度

4 结 论

基于密度泛函理论框架下的第一性原理,本文采用平面波赝势方法分别计算了La,Ce,Nd掺杂单层MoS2的晶格参数、能带结构和态密度、差分电荷密度,并与本征MoS2进行了对比分析.结果表明,La杂质附近的键长变化最大,Nd杂质附近的键长变化最小,分析认为晶格畸变程度的差别与杂质原子的共价半径大小有关.能带结构分析表明,La掺杂可以在MoS2的禁带中引入受主能级,Ce,Nd掺杂可能形成施主、受主能级共存的情况.差分电荷密度分布显示,稀土掺杂可以使单层MoS2中的电子分布发生改变,尤其是f电子的存在会使差分电荷密度呈现出反差极大的物理图像.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004 Science 306 666

[2]Geim A K 2009 Science 324 1530

[3]Geim A K,Novoselov K S 2007 Nat.Mater.6 183

[4]Neto A H C,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[5]Bonaccorso F,Sun Z,Hasan T,Ferrari A C 2010 Nat.Photon.4 611

[6]Mak K F,Lee C,Hone J,Shan J,Heinz T F 2010 Phys.Rev.Lett.105 136805

[7]Liu K K,Zhang W J,Lee Y H,Lin Y C,Chang M T,Su C Y,Chang C S,Li H,Shi Y M,Zhang H,Lai C S,Li L J 2012 Nano Lett.12 1538

[8]Ellis J K,Lucero M J,Scuseria G E 2011 Appl.Phys.Lett.99 261908

[9]Kadantsev E S,Hawrylak P 2012 Sol.Stat.Commun.152 909

[10]Eda G,Yamaguchi H,Voiry D,Fujita T,Chen M,Chhowalla M 2011 Nano Lett.11 5111

[11]Splendiani A,Sun L,Zhang Y,Li T,Kim J,Chim C,Galli G,Wang F 2010 Nano Lett.10 1271

[12]Novoselov K S,Jiang D,Schedin F,Booth T J,Khotkevich V V,Morozov S V,Geim A K 2005 PNAS 102 10451

[13]Zeng Z Y,Yin Z Y,Huang X,Li H,He Q,Lu G,Boey F,Zhang H 2011 Angew.Chem.Int.Ed.50 11093

[14]Coleman J N,Lotya M,O’Neill A 2011 Science 331 568

[15]Lee Y H,Zhang X Q,Zhang W J,Chang M T,Lin C T,Chang K D,Yu Y C,Wang J T W,Chang C S,Li L J,Lin T W 2012 Adv.Mater.24 2320

[16]Radisavljevic B,Radenovic A,Brivio J,Giacometti V,Kis A 2011 Nat.Nanotech.6 147

[17]Radisavljevic B,Whitwick M B,Kis A 2011 ACS Nano 5 9934

[18]Yoon Y,Ganapathi K,Salahuddin S 2011 Nano Lett.11 3768

[19]Yin Z,Li H,Li H,Jiang L,Shi Y,Sun Y,Lu G,Zhang Q,Chen X,Zhang H 2012 ACS Nano 6 74

[20]Tsai D S,Lien D H,Tsai M L,Su S H,Chen K M,Ke J J,Yu Y C,Li L J,He J H 2014 IEEE J.Select.Top.Quant.Elect.20 3800206

[21]Myoung N,Seo K,Lee S J,Ihm G 2013 ACS Nano 7 7021

[22]Zheng J,Zhang H,Dong S H,Liu Y P,Nai C T,Shin H S,Jeong H Y,Liu B,Loh K P 2014 Nat.Commun.(in press)

[23]Dankert A,Langouche L,Mutta V K,Dash S P 2013 ACS Nano 8 476

[24]Dong H M 2013 Acta Phys.Sin.62 206101(in Chinese)[董海明 2013物理学报 62 206101]

[25]Kan M,Wang J Y,Li X W,Zhang S H,Li Y W,Kawazoe Y,Sun Q,Jena P 2014 J.Phys.Chem.C(in press)

[26]Tiwari C,Sharma R,Sharma Y 2012 Proceedings of the 57th Dae Solid State Physics Symposium Mumbai,India,December 3–7,2012 p852

[27]Wu M S,Xu B,Liu G,Ouyang C Y 2013 Acta Phys.Sin.62 037103(in Chinese)[吴木生,徐波,刘刚,欧阳楚英2013物理学报62 037103]

[28]Cao J,Cui L,Pan J 2013 Acta Phys.Sin.62 187102(in Chinese)[曹娟,崔磊,潘靖 2013物理学报 62 187102]

[29]Dar A,Majid A 2013 J.Appl.Phys.114 123703

[30]Li H L,Zhang Z,Lü Y B,Huang J Z,Zhang Y,Liu R X 2013 Acta Phys.Sin.62 047101(in Chinese)[李泓霖,张仲,吕英波,黄金昭,张英,刘如喜2013物理学报62 047101]

[31]Li Q Q,Hao Q Y,Li Y,Liu G D 2013 Acta Phys.Sin.62 017103(in Chinese)[李倩倩,郝秋艳,李英,刘国栋 2013物理学报62 017103]

[32]Hohenberg P,Kohn W 1964 Phys.Rev.136 B864

[33]Kohn W,Sham L J 1965 Phys.Rev.140 A1133

[34]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[35]Pfrommer B G,Cote M,Louie S G,Cohen M L 1997 J.Comput.Phys.131 233

[36]Li Y,Zhou Z,Zhang S,Chen Z 2008 J.Am.Chem.Soc.130 16739