用快速多极方法预测圆柱绕流的气动噪声

刘 超，刘秋洪，蔡晋生

（西北工业大学 翼型叶栅空气动力学国防科技重点实验室，西安710072）

用快速多极方法预测圆柱绕流的气动噪声

刘 超，刘秋洪，蔡晋生

（西北工业大学 翼型叶栅空气动力学国防科技重点实验室，西安710072）

采用声模拟理论预测气动噪声时需要大量的计算时间，快速多极方法将传统点对点计算转变为点集之间的相互作用，可以有效加速计算。基于二维自由空间格林函数的分波展开方式，推导了FW-H方程应用快速多极变换后的积分核函数与计算公式。计算了低马赫数圆柱绕流的非定常流场；并由此预测了气动声源。随后，分别采用传统方法和快速多极方法计算其声场分布。结果表明，基于分波展开方式的快速多极方法能准确计算圆柱绕流气动噪声，在频率较低时能大幅减少声场计算时间，且观测点数越多，加速效果越明显。

声学；气动噪声；数值预测；快速多极；声模拟

快速多极方法[4]对积分核函数引入多极扩展，将源点和场点分离，用节点集之间相互作用取代节点之间一对一计算，使计算量和存储量大幅减少，目前该方法已广泛应用于力学、电磁学等诸多领域。在声学方面，Rokhlin[5]最早使用快速多极方法求解声散射问题，随后国内外很多学者将其与边界元结合用于振动声学计算[6]。然而，在气动声学方面，关于将快速多极方法应用于声模拟理论的文献较少，目前已知Wolf[7—9]利用宽频快速多极方法与声模拟理论相结合，数值计算了圆柱和翼型等流场的气动噪声，但在其文章[7]中仅给出了多极扩展系数的转移公式，而未给出相应的FW-H方程的变换公式。在国内方面，目前为止还没有快速多极方法应用于气动声学计算的公开报道。

本文借鉴Wolf[7]的思路，将快速多极方法应用于声模拟理论，详细推导了FW-H方程应用快速多极变换后的积分核函数与计算公式，并编写相应的计算程序，数值预测了二维圆柱绕流的气动噪声，与传统方法对比验证了快速多极方法的有效性和快速性。

1 气动声学计算的快速多极方法

1.1 传统气动声学计算方法

声模拟理论在忽略声场对流场影响的假设下，将近场非线性流动区域的声源和远场线性区域的声辐射分离求解，其计算流场中固体物绕流诱发气动噪声的FW-H方程[3]为

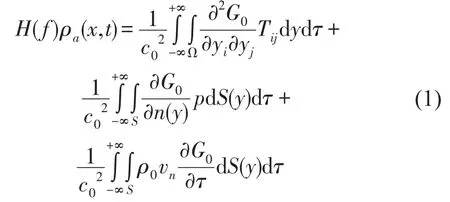
其中H(f)是Heaviside函数，c0是介质中声速，Tij为Lighthill应力张量，G0为自由空间格林函数，p为壁面压力，vn为壁面运动的法向速度，Ω是声源区域，S是固体边界。当边界静止时，式(1)的频域表达式为

1.2 快速多极方法应用于声学控制方程

快速多极方法通过构造自适应四叉树将所有离散的声源点划分成多个点集，然后将积分核函数在树结构的叶子节点处多极展开并计算多级扩展系数，之后通过多极扩展系数转移公式计算每个叶子节点处的局部扩展系数，最后由所有叶子节点处的局部扩展系数计算不同观测点处声压，具体流程如下图1所示：

对于二维问题，式(2)中自由空间格林函数为

设声场点x和声源点y在极坐标系中的表达式为x=(ρx,θx)和y=(ρy,θy)。根据Graf加法定理[10]得零阶第1类汉克尔函数的级数表达式为

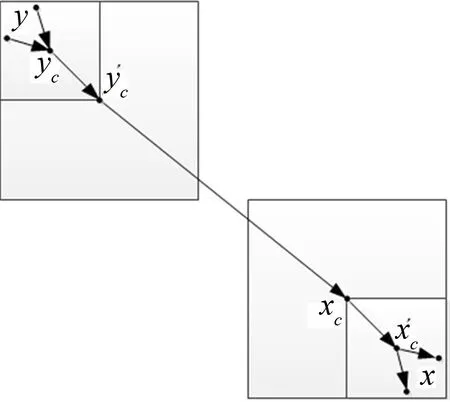
图1 快速多极方法示意图

频率ω固定时，将G0(x,y)在声源点y周围的结构中心yc多极展开为

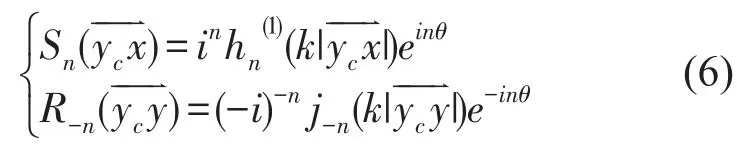
将上述二维自由空间格林函数的多极展开式(5)代入到原频域声学控制方程(2)，得到两个需要重新计算的积分核函数如下

将式(7)代入控制方程(2)，并令多极扩展系数

则式(2)变换为

1.2.1 多极扩展系数转移

当多极展开中心由子正方形中心yc转移到父正方形中心yc'时，多极扩展系数转移按下式计算

可以看出新的多极扩展系数Mn(yc')可以从老的多极扩展系数Mm(yc)计算得到，从而避免了重复计算。通过多极扩展系数的转移可以把同层的子正方形的多极扩展系数总和转移到包含更大边界的父正方形的多极扩展系数中去。此时的频域声学控制方程(9)变换为

1.2.2 局部扩展

当多极扩展系数向局部扩展系数转移，把原配置点y的父正方形的多极扩展系数（中心在yc'）转移到了包含x的父正方形的局部扩展系数（中心在xc）时，局部扩展系数按下式计算

其中Ln(xc)表示中心在xc的局部扩展系数。此时的频域声学控制方程(11)变换为

1.2.3 局部扩展系数转移

当局部扩展中心由父正方形的中心xc转移到子正方形的中心xc'时，局部扩展系数转移按下式计算

通过局部扩展系数转移，将父正方形的局部扩展系数转移到了所包含的子正方形局部扩展系数。此时的频域声学控制方程(13)变换为

在实际计算中，以上公式的无穷级数必须截断，由此引入截断误差并影响声场计算精度。截断项数越多，截断误差越小，声场计算精度越高，但计算时间变长，计算效率下降；若截断项数不足，声场计算则会出现失真。因此需要合理的选择截断项数以同时兼顾计算精度和计算效率。

1.3 快速多极方法的计算过程

1.3.1 建立分层树结构

首先建立根节点使其包含所有流场和声场网格，之后根据每个节点内包含流场和声场网格的数量递归划分四叉树，最后建立邻居节点、相互作用节点和远场节点的索引。

1.3.2 上行遍历计算多极扩展系数

上行遍历指由树结构的叶子节点开始，逐层上行计算所有节点的多极扩展系数，直至第二层。对于叶子节点，直接使用公式(8)计算其多极扩展系数，此时需要计算贝塞尔函数的偏导数及其积分，所需计算时间较长；对于非叶子节点，直接使用公式(10)将子节点的多极扩展系数转移到父节点的多极扩展系数。

1.3.3 下行遍历计算局部扩展系数

下行遍历指由树结构的第二层开始，逐层下行计算出所有节点的局部扩展系数，直至叶子节点。所有节点的局部扩展系数来源于相互作用节点和远场节点两部分贡献量的和。前者的贡献通过公式(12)计算，后者的贡献通过公式(14)计算。

1.3.4 计算总积分

树结构的多极扩展系数及局部扩展系数计算完成后，针对不同的声场观测点，计算两个积分核函数在固体壁面和流体流动区域积分的总和。其中，对于远离声场观测点的流场声源点，使用快速多极算法计算积分；对于临近观测点的声源点则直接计算其积分。

2 算例验证与分析

将上述方法应用于二维圆柱绕流的气动声学计算，使用Fortran 90编写相应的计算程序。

2.1 流场计算模型与结果

流场计算选取直径D=0.019 m的圆柱，均匀来流马赫数为Ma=0.2，雷诺数为Re=9×104，远场采用无反射边界条件，时间推进步长取Δt=2×10-5s，使用k-w SST两方程模型求解湍流雷诺应力，圆柱局部网格如图2所示。

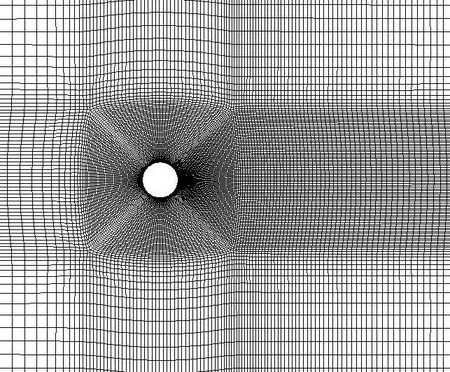
图2 圆柱局部网格

图3给出了圆柱升力系数Cl和阻力系数Cd随时间的变化。可以看出，二维模型所得到的升力系数和阻力系数有规整的周期性波动，其中升力系数的脉动幅值远大于阻力系数，因此卡门涡街中涡脱落形成升力激发的噪声要远大于压差阻力及摩擦阻力引起的噪声。

图4为升阻力系数变化的功率谱密度(PSD)，其中升力系数的基频也即尾涡脱落频率为f0= 897.53 Hz，相应的无量纲斯特劳哈数为St=0.251，与Orselli[11]的计算结果(St=0.235)较符合。此外升力系数较明显的谐波分量为基频的奇数倍，而阻力系数较明显的谐波分量为基频的偶数倍，与Orselli[11]和Takaishi[12]得到的结论一致。

图4 升阻力系数随时间变化的功率谱密度

2.2 声场计算结果与分析

选取36个周期的流场数据输出作为气动声源，采样步长与流场计算的物理时间推进步长一致，总采样步数2 048步，频率分辨率约为24.2 Hz。声场云图计算使用3 000个观测点，布置在以圆柱中心点为圆心，半径10D到128D的环形区域内。自适应四叉树划分时每个叶子节点内最多包含50个声场观测点，得到的自适应树结构共有5层，149个节点，128个叶子节点。

图5为使用传统方法和使用快速多极方法得到的涡脱落频率f=f0下声场观测点位于128D处的声场指向性对比图，其中多极展开的截断项数取p= 20。图中TM-dip和TM-quad表示传统方法得到的偶极子和四极子噪声，FM-dip和FM-quad则表示使用快速多极方法得到的偶极子和四极子噪声。从图中可以看出，偶极子噪声在空间呈正8字形，声压级幅值占优，而四极子噪声则呈现光滑规则的四花瓣状，声压级较小。此外，两种方法得到声场结果一致，验证了本文快速多极方法的准确性。

图5 涡脱落1倍频时声场指向性对比图

图6和图7给出了升力系数变化的基频即涡脱落频率f=f0下声场总声压云图和声压实部，从中可以看出升力脉动引起声场的声压级在空间呈上下对称并沿竖直方向传播，此外，多极展开的截断项数取p=20可以准确计算一倍频下声场声压云图，下面将讨论2倍频时截断项数取值过小导致声场失真的情况。

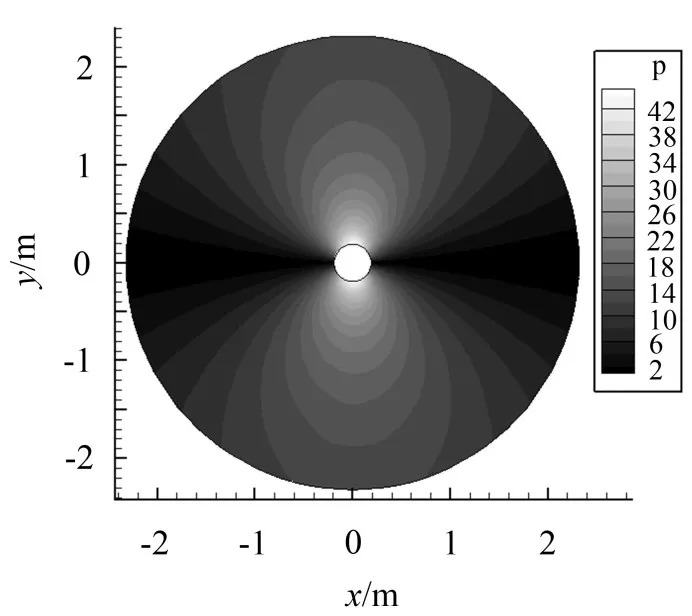
图6 1倍频截断项数p=20时声场云图

图7 一倍频截断项数p=20时声压实部

图8给出了截断项数继续取p=20时涡脱落2倍频f=2 f0下声场总声压云图，可以看出此时部分声场失真，这是由于频率提高，声压量级减小，多极扩展系数所需计算精度提高，截断项数需要相应的增加才能准确计算声场分布。

图8 二倍频截断项数p=20时声场云图

图9和图10给出了p=35时二倍频率下声场总声压云图和声压实部，此时声场呈倒8字，主要由阻力脉动引起，与图4功率谱密度中计算得到阻力系数较明显的谐波分量为基频的偶数倍的结论相符，进一步验证了本文快速多极方法的准确性。

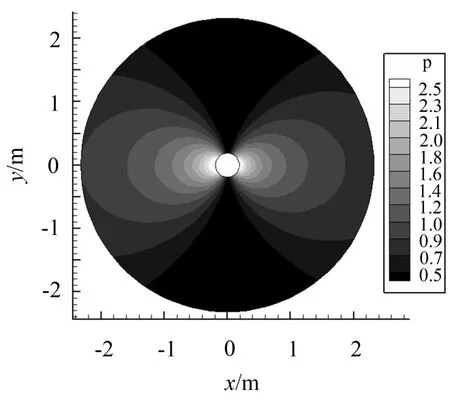
图9 二倍频截断项数p=35时声场云图

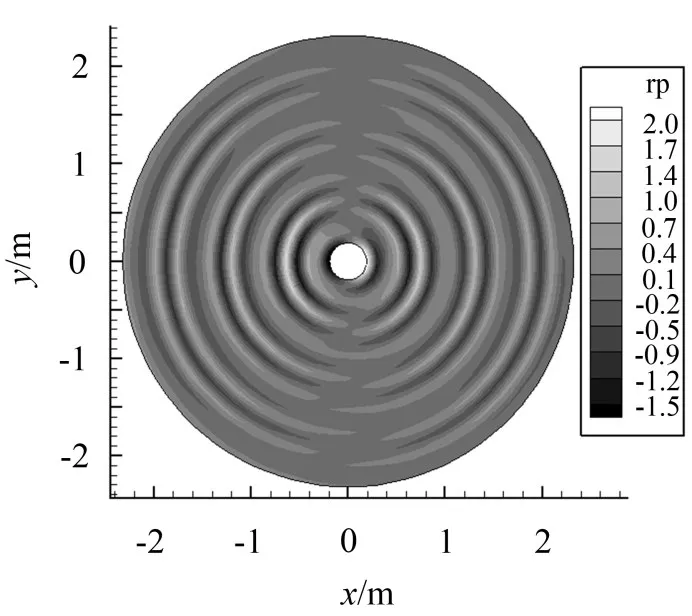
图10 二倍频截断项数p=35时声场实部

图11给出了涡脱落三倍频f=3 f0时声场总声压云图，此时声场恢复正8字形状，对应升力系数脉动的2次谐波分量，但声压量级远远小于一倍频，使用快速多极方法取截断项数p=50计算得到声场结果仍有轻微的失真。

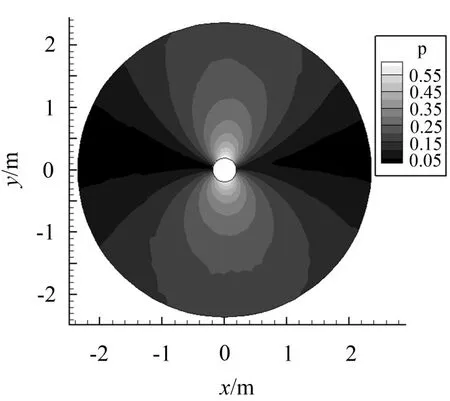
图11 三倍频截断项数p=50时声场云图

表1列出了在圆柱绕流涡脱落的前3个整数倍频下使用传统方法和使用快速多极方法求解FW-H方程所需要的计算时间对比。从表中可以看出，使用传统方法计算3个频率下的声场所需时间差别不大，而使用快速多极方法在频率较低时能大幅缩减声场计算时间，有很高的实用价值和工程应用前景。

表1 快速多极方法加速效率

在1.3.2节提到，对于叶子节点，计算其包含的所有声源点在该叶子节点处的多极扩展系数时，需要计算贝塞尔函数的偏导数及其积分，所需计算时间较长，而由叶子节点的局部扩展系数计算观测点处声压时需要的时间较短，所以观测点数量增多对整体计算时间影响较小。下表列出了涡脱落一倍频时，观测点数量变化导致快速多极方法加速计算效率变化的比较，从中可以看出，基于分波展开方式的快速多极方法特别适合于广域空间内大量声场点的声压计算。

表2 声场观测点数量对加速效率的影响

3 结语

(1)快速多极方法通过格林函数的多极展开将声源点和观测点分离，通过构造自适应四叉树使传统FW-H方程中格林函数点对点积分转化为点集之间的相互作用，从而使声场计算时间大幅缩短；(2)本文使用的分波展开方式由流场信息计算叶子节点的多极扩展系数时所需时间较长，由叶子节点的局部扩展系数计算观测点处声压时需要的时间较短，因此声场观测点数越多，加速效果越明显；

(3)随着频率提高，声压量级降低，需要增大多极截断项数来准确计算声场分布，导致高频时加速效率下降，但工程中往往更关注声压级较高的低频噪声问题，因此本文快速多极加速计算方法具有实际应用价值。

[1]Lighthill M J.On sound generated aeroynam ically.I.general theory[J].Proceedings of the Royal Society of London,SeriesA,1952,A211:564-587.

[2]Lighthill M J.On sound generated aerodynam ically.II.Turbulence as a source of sound[J].Proceedings of the Royal Society of London,Series A,1954,222:1-32.

[3]Curle N.The influence of solid boundaries on aerodynam ic sound[J].Proceedings of the Royal Society of London,SeriesA,1952,213,1187:505-514.

[4]Greengard L,Rokhlin V.A fast algorithm for particle simulations[J].Journal of Computational Physics.1987, 73:325-348.

[5]Rokhlin V.Rapid solution of integral equations of scattering theory in two dimensions[J].Journal of Computational Physics,1990,86:414-439.

[6]崔晓兵，季振林，武 耀.快速多极子边界元法预测船舶舱室噪声[J].噪声与振动控制，2012，32(6)：179-183.

[7]Wolf W R,Lele S K.Acoustic analogy formulations accelerated by fast multipole method for two-dimensional aeroacoustic problems[J].AIAA Journal,2010,48(10): 2274-2285.

[8]Wolf W R,Lele S K.Aeroacoustic integrals accelerated by fast multipole method[J].AIAA Journal,2011,49(7): 1466-1477.

[9]Wolf W R,Lele S K,Jothiprasad G,Cheung L.Investigation of noise generated by a DU 96 airfoil[C].18 th AIAA/CEAS Aeroacoustics Conference,Colorado Springs,CO,2012,2012-2055.

[10]Abramow ita M,Stegun I A.Handbook of mathematical function[M].New York:Dover,1965.

[11]Orselli R M,Meneghini J R,Saltara F.Two and threedimensional simulation of sound generated by flow around a circular cylinder[J].AIAA paper,2009,3270.

[12]Takaishi T,M iyazawa M,Kato C.Computational method of evaluating noncompact sound based on vortex sound theory[J].Journal of Acoustical Society of America, 1998,233-253.

Fast Multipole Method Applied in Prediction ofAeroacoustics Induced by a Circular Cylinder

LIU Chao,LIU Qiu-hong,CAI Jin-sheng

(National Key Laboratory of Aerodynam ic Design and Research, Northwestern Polytechnical University,Xi’an 710072,China)

Prediction of aeroacoustics using acoustic analogy is a time-consum ing process,while the fast multipole method which changes traditional way of node-to-node computing into set-to-set interaction can accelerate the process effectively.In this paper,the FW-H equation and its integral kernel function are derived w ith the fast multipole method based on the partial-wave expansion formulation of free-space Green’s function.The unsteady flow field w ith low Mach’s number near a two-dimensional circular cylinder is computed and exported as the sound source,and the sound field is obtained via traditional method and the fast multipole method.The results show that the fast multipole method based on partial-wave expansion can calculate the aerodynam ic noise accurately,and reduce the computing time greatly for relatively low frequencies.And the acceleration effect is more obvious w ith larger number of observers.

acoustics;aerodynamic noise;numerical prediction;fast multipole method;acoustic analogy

1006-1355(2014)04-0123-05+133

O42 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.027

随着国内外商用飞机的迅速发展，飞机噪声预测与控制受到人们的普遍关注，基于计算流体力学的计算气动声学逐渐成为研究热点。然而，传统的气动声学混合计算方法[1—3]需要计算所有流场声源点和远场观测点之间格林函数的偏导数及其积分，这个过程需要大量的计算时间，而应用于飞机噪声预测等大规模声学计算问题的计算耗时更是难以接受，因此发展快速和有效的气动噪声计算方法越来越受到人们的重视，同时也具有十分重要的工程应用价值。

2013-10-30

国家自然科学基金(基金编号：11002116)

刘超（1990-），男，河北沧州人，硕士研究生，主要研究方向为计算流体力学和气动声学计算。

E-mail:lc1990@mail.nwpu.edu.cn