TBM液压直管道的非线性动力学特性研究

齐征宇，张怀亮1，，彭 欢

(1.中南大学 高性能复杂制造国家重点实验室，长沙410083；2.中南大学 机电工程学院，长沙410083)

TBM液压直管道的非线性动力学特性研究

齐征宇2，张怀亮1，2，彭 欢2

(1.中南大学 高性能复杂制造国家重点实验室，长沙410083；2.中南大学 机电工程学院，长沙410083)

针对TBM掘进过程中产生的振动对液压管道的影响，以液压直管为研究对象，在考虑管道变形的几何非线性及流体脉动的情况下，建立系统的非线性运动微分方程，运用Galerkin方法对其进行离散化，采用数值仿真方法分析基础振动振幅及频率对系统非线性动力学特性的影响规律。结果表明随着基础振动频率和幅值的变化，管道系统交替呈现周期和混沌运动两种形态。系统通过系列倍周期分岔或阵发性混沌进入混沌，通过倍周期倒分岔脱离混沌；当传递到管道上的基础振动频率低于42 Hz时，或者当传递到管道上的基础振动幅值D在(0，2.5)和(6.5，8.4)mm区间时，可以有效避免系统混沌运动的产生，增加管道运动的稳定性。

振动与波；直管道；基础振动；非线性；分岔；混沌

很多学者致力于输流管道的非线性动力学行为的研究，并取得了很多有益的研究成果。针对两端支承管道，Holmes[3]利用Lyapunov直接法严格证明了两端固支的输液管道在自激作用下不可能发生颤振。Namchchivaya[4]应用平均法研究了脉动内流作用下两端固定管道的次谐波共振及组合共振。邹光胜[5―8]研究了两端固定输流管在基础谐激励作用下的混沌运动，考察了流体流速和激振频率对管道振动特性的影响，并研究了输送脉动流管道在基础振动下的分岔行为，重点探讨了流体平均流速、流速脉动振幅对系统动态特性的影响。金志浩[9,10]利用非线性动力学分析方法，研究了两端弹性支承输流直管道系统在自激-参数激励-外激励联合作用下的非线性动力学行为。梁峰[11]采用实验方法对两端支承输流管在脉动内流作用下的参数共振问题和支承激励作用(定常流)下的强迫振动问题进行了研究。张艳雷[12]研究了输流管的分岔特性，得出管内流体因振荡流作用而产生自激振动是分岔与混沌运动的原因。但是针对两端固定输流管道在基础振动及流体脉动联合作用下的非线性振动特性鲜有研究。

本文以两端固定输流管道为研究对象，考虑流体脉动、基础振动及横向弯曲引起的非线性轴向力作用的影响，采用数值仿真方法研究了基础振动振幅及频率对系统振动响应的影响，为TBM液压管道的振动控制提供一定的理论依据。

1 系统运动方程及其离散化

1.1 系统运动方程

将TBM液压直管道简化为两端固定支承直管模型进行研究，理论模型如图1所示。输流管道水平固定在基础上，并且基础也做简谐运动，其运动方向垂直于管道轴线，即

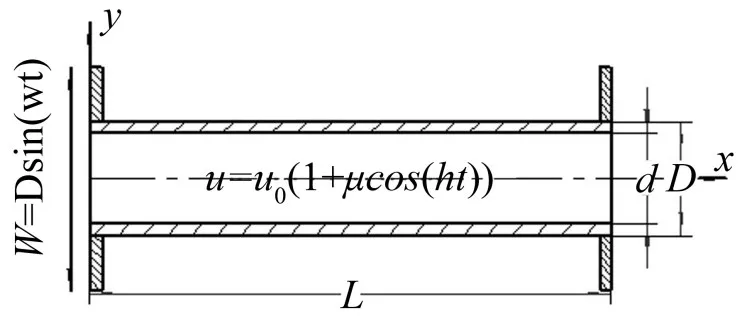
图1 管道理论模型

W=Dsin(ωt)，其中D为激振幅值，ω为激振频率。考虑了横向弯曲时引起的附加非线性轴向力项[13]和管道材料的Kelvin-Voigt粘弹性[14]，运用达朗伯原理和牛顿定理，得到基础振动下输流管道的非线性运动微分方程[15]

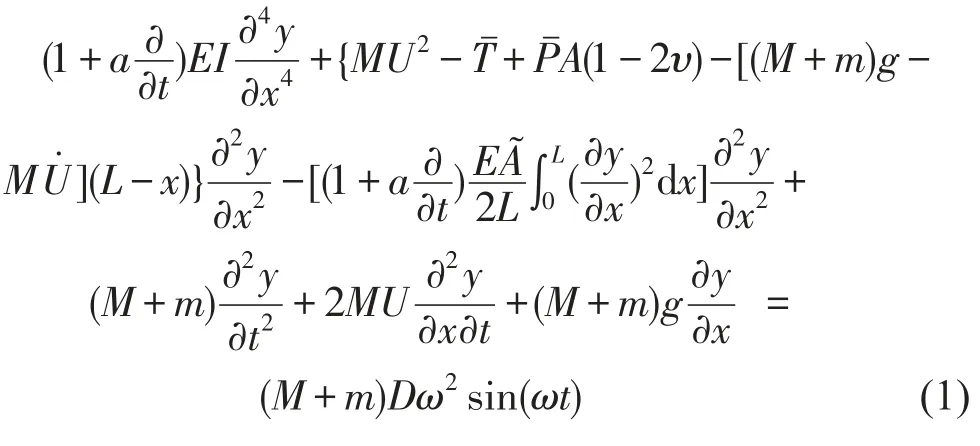
式中，a为管道黏弹性系数，L为管道长度，U为管道内流体流速，M为单位长度流体质量，m为单位长度管道质量，EI为管道抗弯刚度，Tˉ为轴向力，Pˉ为流体压强，υ为泊松比，g为重力加速度，A˜为管道有效横截面积，A为管道过流截面积，t为时间。

引入如下无量纲参数

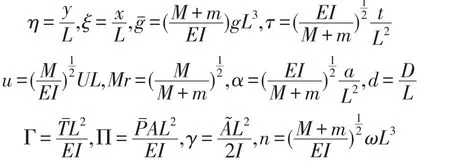
在工程实际中，TBM输流管道内流体是由柱塞泵提供的一种脉动形式的流体，故可将该流速描述成以下无量纲化的形式，即

式中u0为流体的平均流速，μ为流体的脉动幅值，ω1为流体的脉动频率。将上述无量纲参数及式(2)带入式(1)中，得到基础简谐激励及脉动流联合作用下输流管的运动微分方程

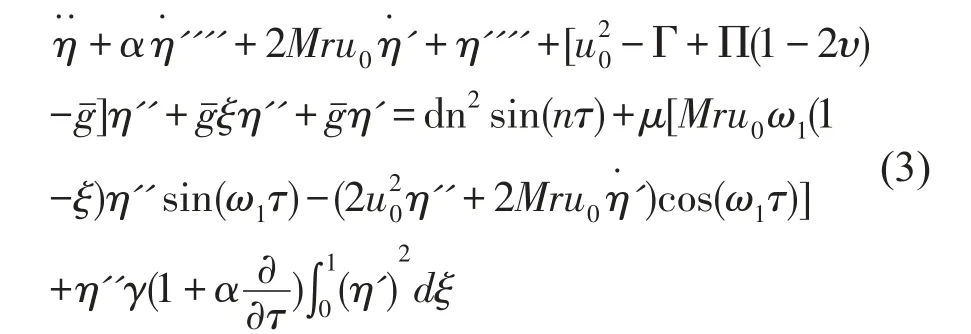
1.2 运动微分方程的离散化

为了便于求解系统的运动偏微分方程，通常采用Galerkin展开式将无量纲化的偏微分方程(3)进行离散化处理，将其降阶为低次的常微分方程组。故设Galerkin展开式为

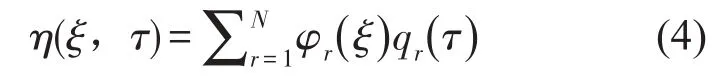
式中φr用相同边界条件下梁模型的模态函数来近似代替输流管的模态函数，qr(τ)为对应的广义坐标，N为模态截断数，且有

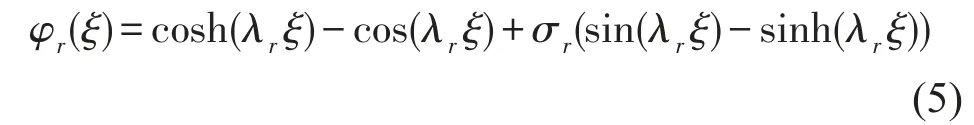
其中 λ1=4.7300;λ2=7.8532;且σr=(cosh(λr)-cos(λr))/((sin(λr)-sinh(λr))。

因为取前两阶振型即可满足精度要求[10]，故在方程(4)中取N=2，则Galerkin 2阶展开式为

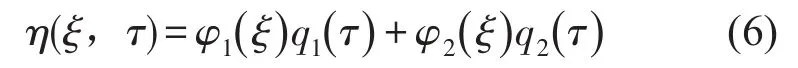
并令T=Γ-Π(1-2υ)，因为重力只会对振动的平衡位置产生影响，对其他的振动特性没有影响，故可以忽略重力的作用[16]，令gˉ=0。引入状态参数x1，x2，x3，x4，经过一系列复杂的数学推导计算，设X=[x1, x2,x3,x4]T=[q1,q2,q3,q4]T，可将2阶微分方程组降阶为1阶微分方程组，令F(X)=[0，0，F3，F4]T。即有1阶线性微分方程组

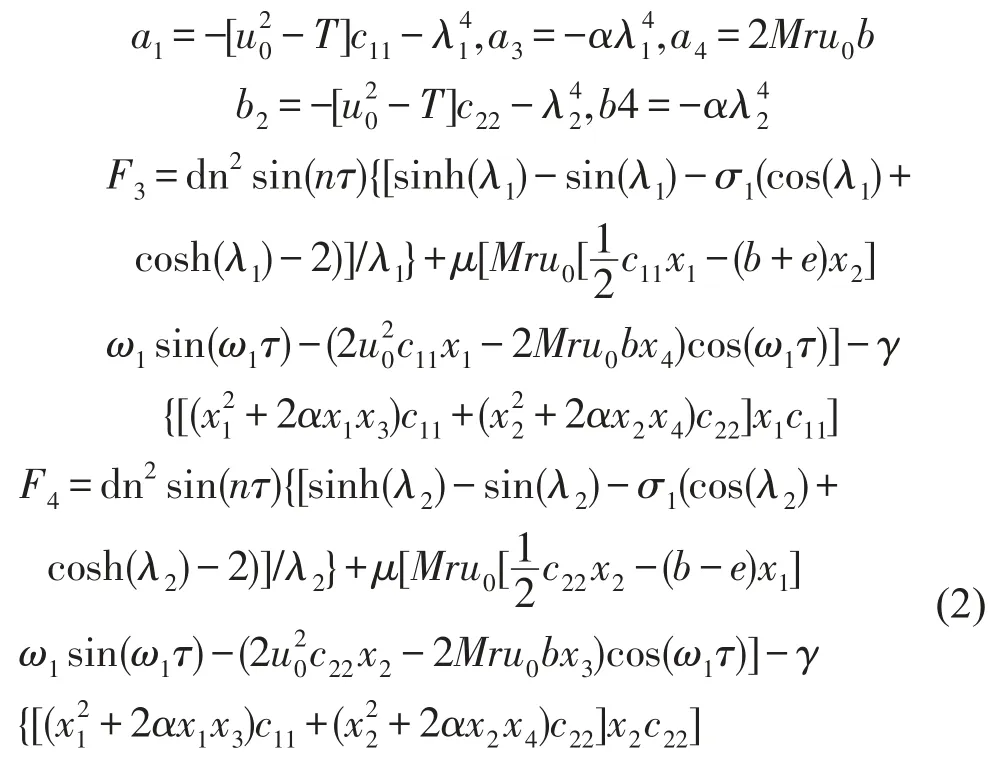
2 仿真分析

根据TBM管道工作参数，设置系统参数如表1所示。

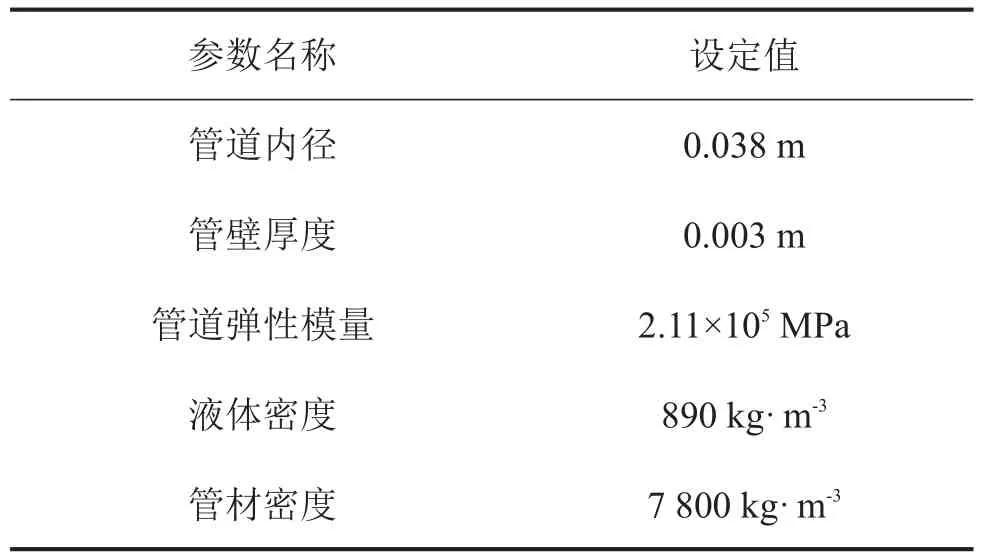
表1 系统参数

无量纲化后的数值仿真参数为

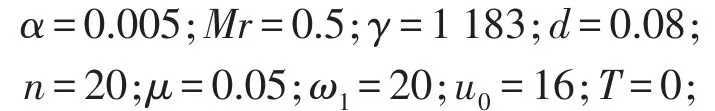
当某一参数作为分岔参数时，此参数取变化的值。采用龙格—库塔法对方程组(7)进行迭代计算，通过分岔图、相图、功率谱图分析系统的非线性动力学行为。初始条件取

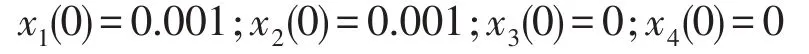
本文在绘制分岔图过程中使用的触发条件是输流管道在中点ξ=0.5位置处的速度从正向趋于零，

2.1 基础振动频率的影响

以基础振动频率n为分岔参数，绘制分岔图(图2)。从分岔图中可以大体看出管道系统运动的分岔路径，但是某些具体的运动形态不能显示出来，因此需要做相图(图3)和功率谱图(图4)来进一步分析系统的动力学响应。图3与图4中的(a)，(b)，(c)，(d)，(e)，(f)分别对应于控制参数n=10，n=30.5，n=40，n=60，n=70，n=95。

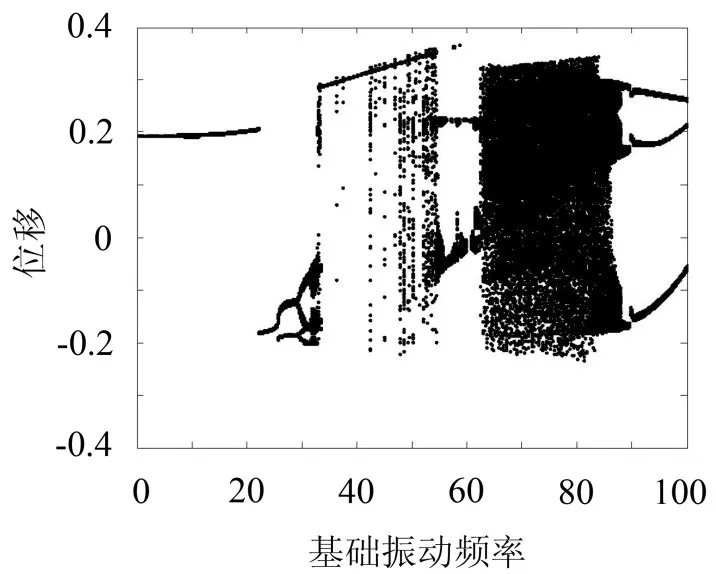
图2 基础振动频率参数区域的分岔图

本文利用功率谱图来区分混沌与周期运动，当系统表现为周期运动时，功率谱图曲线仅有一些狭窄的谱尖点；当系统出现混沌运动时，功率谱图曲线则表现为明显的宽频性质，并伴随噪声背景。因此从分岔图(图2)、相图(图3)和功率谱图(图4)可以看出，两端固定管道系统对于基础振动频率的响应规律，在振动频率较小时(n＜22)，管道系统表现为周期1运动，随着频率的增大，管道运动将发生跳跃现象，体现为围绕另一平衡点的周期1运动，然后在(n=25)是出现周期2运动，且在(n=29.5)时出现了系列倍周期分岔现象，随着频率的进一步增大，系统在(n=64)经由阵发性混沌进入混沌运动状态，频率再增大(n＞88)，管道系统运动最终通过倍周期倒分岔离开混沌运动区域，转化为周期3运动。当传递到管道上的基础振动频率n＜64(转换为有量纲的值为42 Hz)时，系统将不会出现混沌等复杂运动，而是处于稳定的周期运动状态。

2.2 基础振动幅值的影响

以基础振动幅值d为分岔参数，绘制分岔图(5)、相图(图6)和功率谱图(图7)来分析系统的动力学响应。图6与图7中的(a)，(b)，(c)，(d)，(e)，(f)分别对应于控制参数d=0.01，d=0.03，d=0.055，d=0.063，d= 0.075，d=0.086。

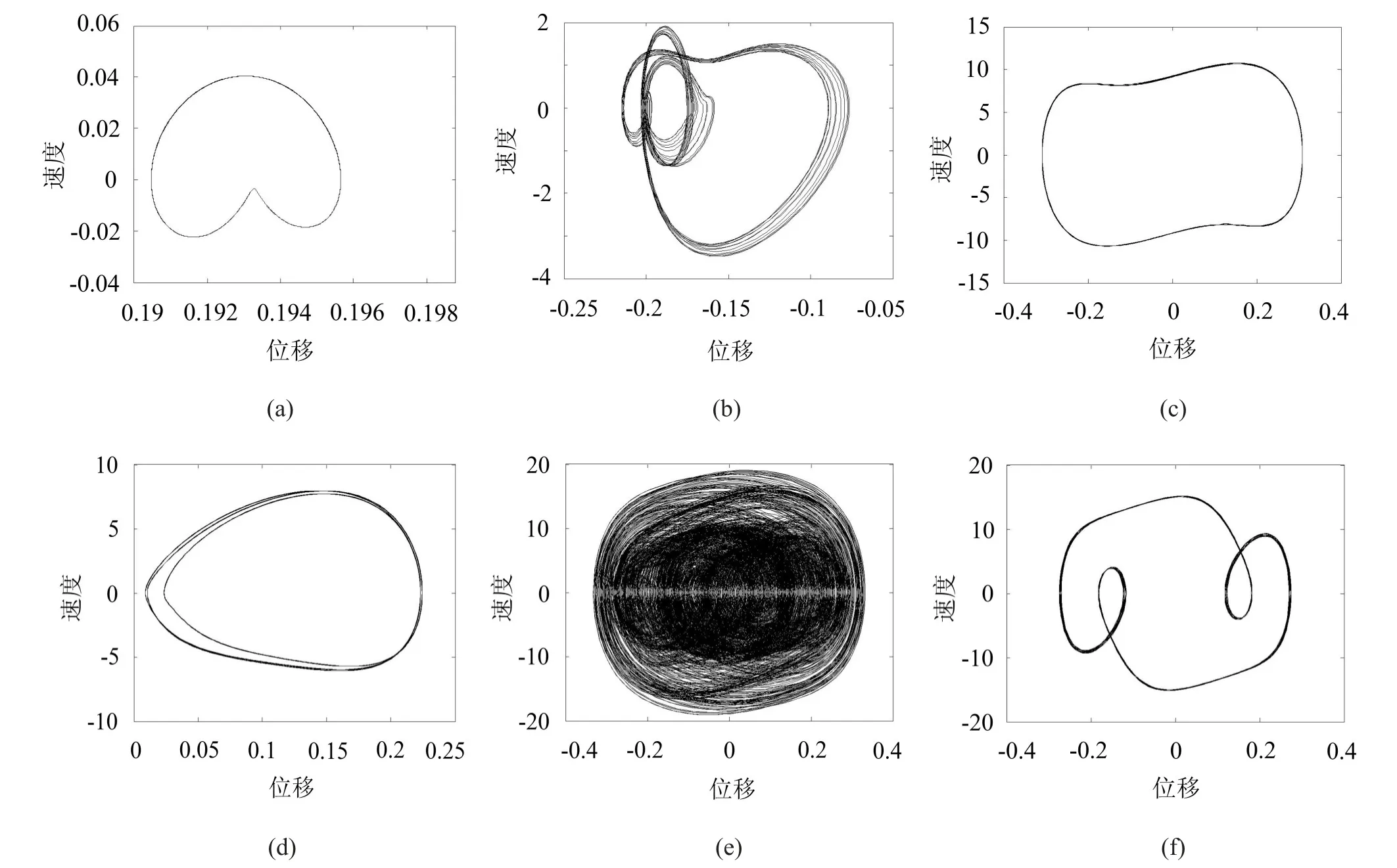
图3 不同基振频率下管道的相平面图

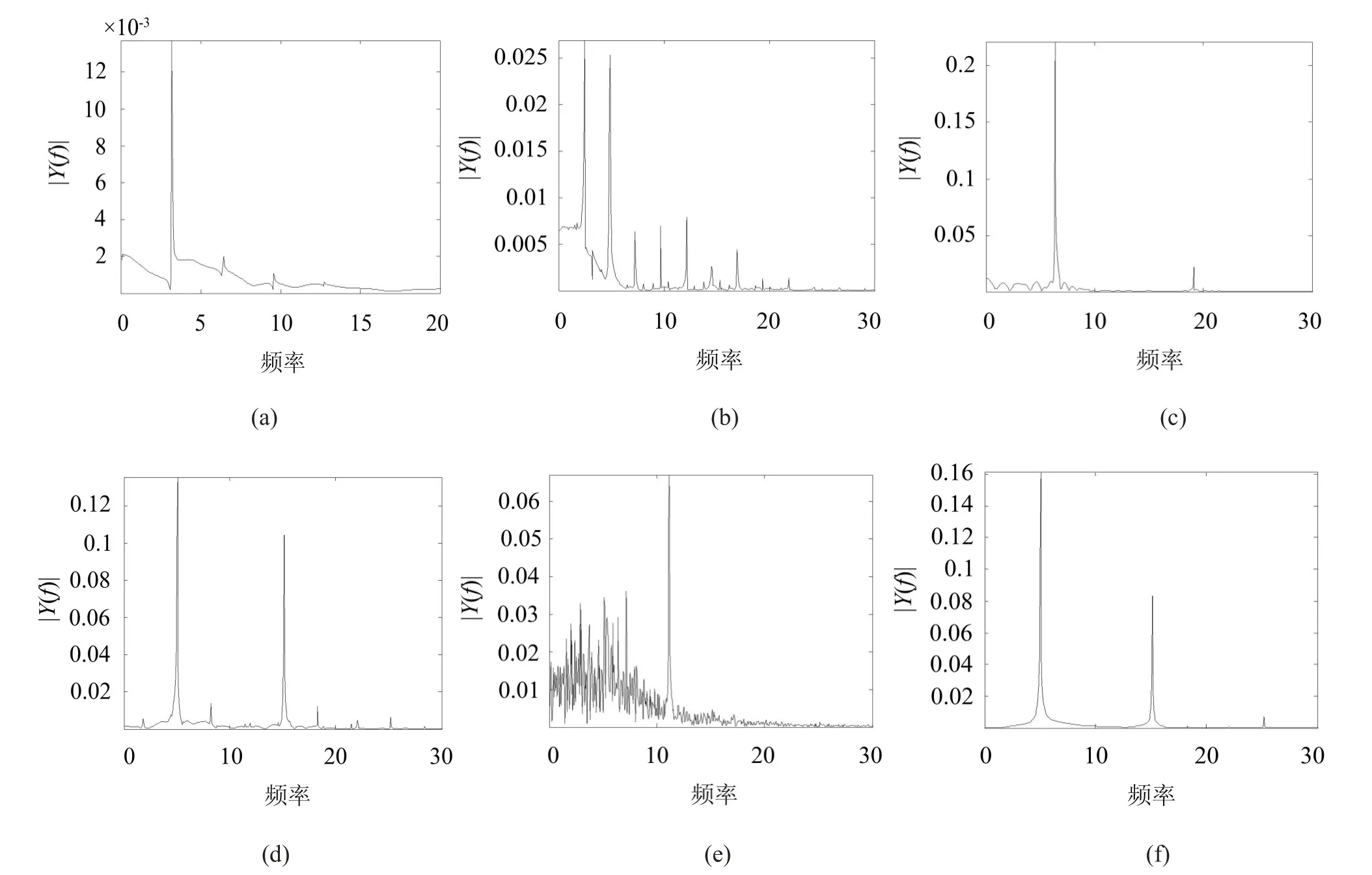
图4 不同基振频率下管道的功率谱图

从基础振动幅值参数区域的分岔图(图5)、不同基振幅值下管道的相图(图6)和功率谱图(图7)可以看出，当基础振动幅值较小时(d＜0.025)，管道发生周期1运动，随着振动幅值的增大(0.025＜d＜0.064)，系统经由阵发性混沌进入一个较宽的混沌区域，在这个混沌区域中，系统出现了几个周期窗口，随着振动幅值的进一步增大(0.064＜d＜0.084)，系统的运动出现通过倍周期倒分岔转化为周期3运动，在d= 0.084时，系统响应出现倍周期分岔，使得系统在d= 0.09时再次进入混沌运动。当传递到管道上的振动幅值d处于[0，0.025]和[0.065，0.084](转换为有量纲的值为[0，2.5]mm和[6.5，8.4]mm)区间时，系统将处于稳定的周期运动状态。

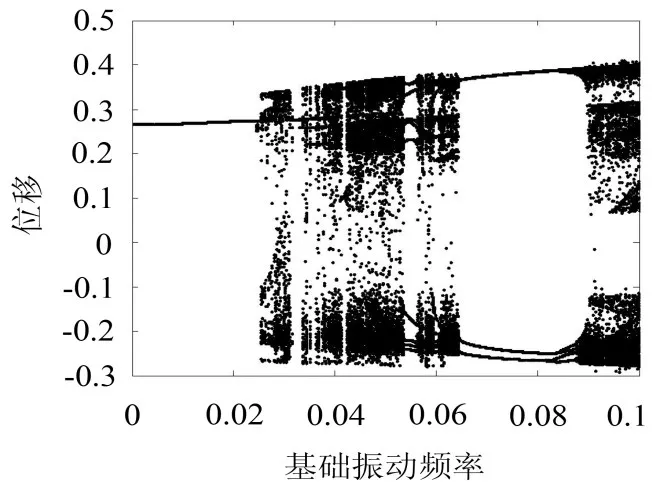
图5 基础振动幅值参数区域的分岔图

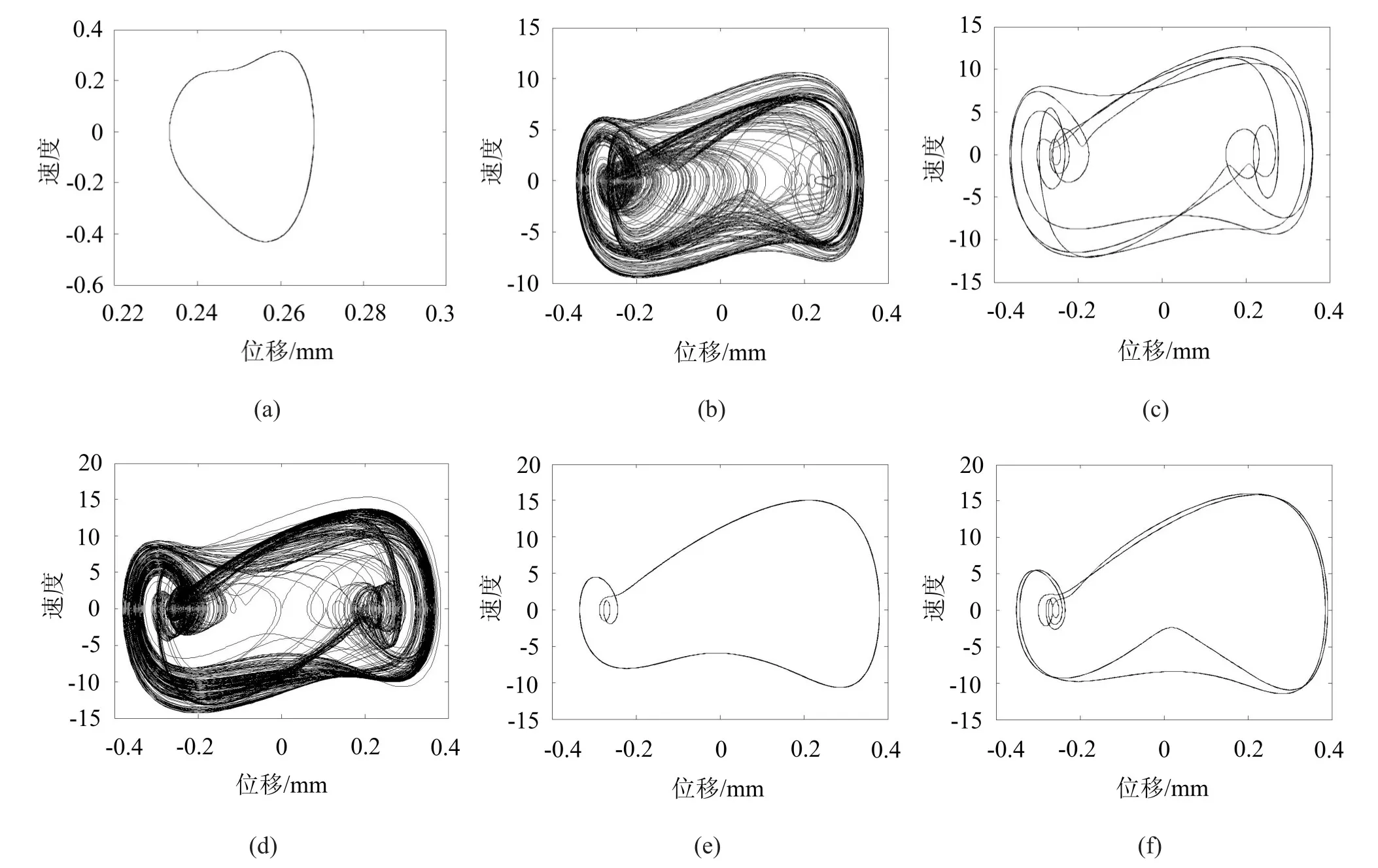
图6 不同基振幅值下管道的相平面图

3 结语

通过对脉动内流及基础振动联合作用下的两端固定直管的仿真计算，得出如下结论：

(1)在基础振动频率n＜64时，系统首先表现为周期运动，随着频率的增大，系统经由阵发性混沌而进入混沌运动状态，又经由倍周期倒分岔而转化为周期运动；

(2)随着基础振动幅值的增大，管道响应首先表现为周期运动，然后通过阵发性混沌途径进入混沌运动，又经由倍周期倒分岔转化为周期运动，之后再次通过倍周期分岔而进入混沌运动状态；

(3)将基础传递到管道上的振动幅值或频率控制在一定的水平，能有效避免系统混沌运动的产生。当基础振动频率ω＜42 Hz时，或者当基础振动幅值D在区间[0，2.5]和[6.5，8.4]mm时，系统将处于稳定的周期状态中。

[1]陈立和.浅析机械应用中的TBM与液压系统[J].吉林省教育学院学报，2011,27(2)：138-139.

[2]陈炳瑞，冯夏庭，曾雄辉，等.深埋隧洞TBM掘进微震实时监测与特征分析[J].岩石力学与工程学报，2011，30 (2)：275-283.

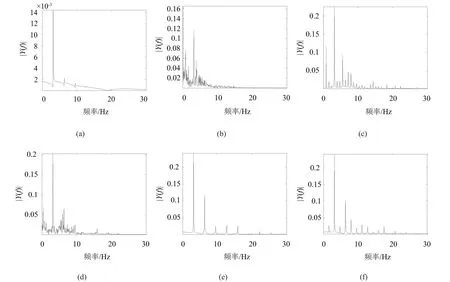
图7 不同基振幅值下管道的功率谱图

[3]Holmes P J.Pipes supported at both ends cannot flutter[J].Journal ofApplied Mechanics,1978,45:619-622.

[4]Namchchivaya N S，Non-linear dynamics of supported pipe conveying pulsating fluid subharmonic resonance[J].International Journal of Non-linear Mechanics,198,24(3): 185-196.

[5]邹光胜，金基铎，闻邦椿.支承运动激励下两端固定输流管道的混沌运动[J].非线性动力学学报，2001，8(1)：27-32.

[6]邹光胜，金基铎，闻邦椿.粘弹性输流管混沌运动的多模态分析[J].东北大学学报，2003，24(2)：132-135.

[7]邹光胜，金基铎，闻邦椿.Melnikov方法在输流管混沌运动研究中的应用[J].力学与实践，2004，26(2)：29-32.

[8]邹光胜，金基铎，闻邦椿.参—强激励联合作用下输流管的分岔和混沌行为研究[J].应用力学学报，2005，22 (1)：111-113.

[9]包日东，金志浩.分析一般支承输流管道的非线性动力学特性[J].振动与冲击，2008，27(7)：87-90.

[10]包日东，金志浩，闻邦椿.一般支承条件下输流管道的非线性动力学特性研究[J].振动与冲击，2009，28(7)：153-157.

[11]梁 峰.输流管道振动特性的实验研究[D].沈阳航空工业学院，2006.

[12]张艳雷.振荡流作用下受约束的悬臂输流管的分岔特性[J].噪声与振动控制，2010，5：46-49.

[13]Semler C,Li G X.P aidoussis M P The non-liner equations of motion of pipes conveying fluid[J].Journal of Sound and Vibration，1994(05).

[14]Jin J D,Zou G S.Bifurcations and chaotic motions in the autonomous system of a restrained pipe conveying fluid [J].Journal of Sound and Vibration,2003,260:783-805.

[15]ZOU Guang-sheng,JIN JI-duo.Stability and chaotic vibrations of a pipe conveying fluid under harmonic excitation[J].Journal of Shanghai University,2000,4(3): 179-185.

[16]唐 冶，方 勃，张业伟.非线性弹簧支承悬臂输液管道的分岔与混沌分析[J].振动与冲击，2011，30(8)：269-274.

Research of Nonlinear Dynamic Characteristics of TBM Hydraulic Straight Pipeline

QI Zheng-yu2,ZHANG Huai-liang1,2,PENGHuan2

(1.State Key Laboratory of High Performance and Complex Manufacturing,Central South University, Changsha 410083,China; 2.College of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)

The influence of foundation vibration in the TBM tunneling process on a hydraulic pipeline is studied.Considering the geometrical nonlinearity of the pipeline deformation and fluid pulsation,the nonlinear dynamic differential equation of the hydraulic straight pipeline is established.Then,this nonlinear differential equation is discretized by Galerkin method.The influence of the amplitude and frequency of the foundation vibration on the nonlinear dynamic features of the pipeline system is analyzed numerically.The results obtained show that the system response is the alternative periodic motion and chaotic motion with the frequency and amplitude of the foundation vibration varying.The response of the system gets into the chaotic motion via series period-doubling bifurcation or intermittent chaos,and it gets back into the periodic motion via series of inverse period-doubling bifurcation.When the frequency of the foundation vibration which transmits to the pipeline is less than 42 Hz or the amplitude D is in the ranges of 0-2.5 mm and 6.5-8.4 mm,the chaotic motion can be effectively avoided,and the stability of the pipeline system movement can be increased.

vibration and wave;straight pipeline;foundation vibration;nonlinear;bifurcation;chaos

1006-1355(2014)03-0061-06

O322

A

10.3969/j.issn.1006-1335.2014.03.013

硬岩掘进机(TBM)是专用于硬岩隧道掘进的专业化装备[1]。因硬岩地质环境的影响，在其作业过程中不可避免的会产生强烈的振动[2]，强振动容易导致液压管路的剧烈振动，影响TBM的工作效率，甚至导致管道的破坏。因此，研究基础振动下液压管道的非线性动力学特性具有重要的工程意义。

2013-08-20

国家重点基础研究发展计划资助项目(2013CB035404)

齐征宇(1986-)，男，硕士生，研究方向：基础振动下液压管道非线性动力学。

E-mail:qizhengyu138@163.com