汽车排气消声器声学性能仿真研究

王新彦, 唐 博, 袁春元, 邱忠华

(1.江苏科技大学 机械工程学院，江苏 镇江 212003)(2. 南京军区联勤部 军事交通运输部, 江苏 南京 210016)

汽车排气消声器声学性能仿真研究

王新彦1, 唐 博1, 袁春元1, 邱忠华2

(1.江苏科技大学 机械工程学院，江苏 镇江 212003)(2. 南京军区联勤部 军事交通运输部, 江苏 南京 210016)

基于三维声波波动方程的有限元软件LMS Virtual.lab Acoustics,采用两种不同的研究方法获得了消声器的传递损失,第1种方法是采用定义入口单位质点振速的方法;第2种方法是采用AML(Automatically Matched Layer)技术直接计算声功率的方法.结果表明两种方法计算出来的结果高度一致,且第2种方法计算步骤简单、计算速度快,对于大截面管路消声器也同样适用.相对传统的传递矩阵法和依靠经验的方法,用三维声学有限元法,在计算速度上有很大的提高,并且有效地减少了基于一维平面波理论所产生的消声器传递损失计算误差.最后利用第2种方法,研究了基于气流速度影响的消声器出口辐射噪声,并建立了其插入损失的有限元计算模型.

传递损失; 声压; 声功率; 辐射噪声; 插入损失

排气噪声是汽车发动机主要噪声源,排气尾管噪声不仅影响汽车车外噪声的大小,同时也是评判排气噪声控制水平的依据[1-2].控制汽车发动机排气噪声的主要途径是安装排气消声器,它是一种阻止声音传播而允许气流通过的降噪装置,其消声器性能直接影响尾管噪声大小.

在评价单个消声元件的消声效果或者初步评价系统的消声性能时,通常用传递损失作为评价指标.当前消声器的设计主要依靠基于一维平面波理论的传递矩阵法,其高度依赖设计者经验知识和试验方法,由于设计者经验的差异和不断重复的试验,导致产品的研发周期较长、成本较高[3-5].而且消声器的内部声场为三维,因此传统上采用一维平面波理论进行设计就必然产生误差.

针对上述问题,文中利用三维声波波动方程的有限元计算方法进行了消声器声学性能研究.首先采用在入口处定义单位质点振速的方法来计算消声器的传递损失，结果发现这种方法计算步骤多、速度慢,存在一定的局限性,且对于大截面管路消声器边界条件不适用.因此提出了一种新的计算传递损失的方法,即通过采用AML技术直接计算声功率来获得消声器传递损失，最后得到基于气流速度影响的消声器出口的辐射噪声.

1 消声器有限元模型

有限元法(finite element method,FEM)是求解各种复杂数学物理问题的重要方法.有限元分析的基本过程是:将介质的复杂几何区域离散为具有简单几何形状的单元,而单元内的材料性质和控制方程通过节点的未知量来进行表达,通过单元组装外载荷和约束条件的处理,得到线性方程组,求解该线性方程组就可以得到该场变量的近似表达,有限元法不仅计算精度高,而且能适应各种复杂的结构形状和复杂的材料特性,因而在实际工程计算中得到广泛应用[6].

文中选择有限元方法计算消声器的声学性能,对介质及声传播过程作以下基本假设:

1)消声器中的媒质为理想流体无粘滞性,声波在介质中传播没有能量损耗；

2)传播过程为绝热过程,与外界不存在热交换;

3) 消声器管道壁面无振动,声能不能沿管道向外透射;

4)介质中传播的是小振幅声波, 介质中各种声场参数都是一阶微量,可用线形波动方程来描述.

对声波在消声器内的传播,应满足三维声波方程,根据理想流体介质的3个基本方程:运动方程、连续性方程和物态方程,可以推导出声波振动的三维声学方程:

2p=

(1)

式中:p,c分别为声压和声速;2为拉普拉斯算子,它在直角坐标系的表达式为2=++.

声压随时间t做简谐振动.令声压p=p(x,y,z)ejωt，并代入式(1),利用变量分离方法得到Helmholtz方程:

2p+k2p=0

(2)

式中:k=ω/c，k和ω分别为声波的波数和角频率.

1.1 消声器的结构模型

图1为消声器内部结构模型,其为抗性消声器.抗性消声器借助于管道截面的扩张或收缩,或旁接共振腔,利用声波的反射、干涉或共振达到消声目的.此消声器共有3个腔体,左边是入口,右边是出口.气流从入口管直接进入第三腔,然后依次通过2个插入管流入第二腔到达第一腔,最后气流通过出口管直接流出.

图1 消声器三维几何模型Fig.1 3-D geometrical model of the muffler

1.2 消声器声学有限元模型

文中在LMS Virtual.lab建立消声器的有限元模型.消声器的有限元网格是内部的空气网格,只需要建立消声器内部介质的仿真模拟.采用LMS Virtual.lab Acoustic进行流体模型分析时,需要考虑声波的反射、衍射和折射等行为,因此计算结果与实际结果之间存在一定误差,这是由于材料定义不准确、几何建模精度不够、边界条件定义不准确等因素造成的,更重要的是在对声场划分网格时,网格划分过于粗糙也会产生较大的误差.因此,为保证计算精度,对于线性模型划分的最大单元的边长应小于计算频率最短波长的1/6,或者要小于最高频率点波长的1/6.图2是消声器声学有限元模型,网格采用四面体结构.

图2 消声器声学有限元模型Fig.2 Acoustic FEM model of muffler

假设声音在某流体介质中的传播速度为c,对于空气,声速c取340m/s,某个单元的长度为L,给定单元是线性单元,那么这个单元可以计算的最大频率为:

(3)

如果知道该模型的最大计算频率fmax,那么所有单元的长度L满足

(4)

文中研究的消声器,最低频率设置为20Hz,最高频率设置为3000Hz.为了提高计算精度,单位长度设置为8mm.划分四面体网格后,VL软件可自动统计出当前有限元模型情况.图3为声学网格计算频率分布，由图3可以看出100%单元的计算上限频率都能达到3177.4 Hz,还有20%的单元能够计算到5897.6Hz.完全满足上限频率为3000Hz的精度要求.

图3 声学网格计算频率分布Fig.3 Calculational frequency distribution ofAcoustic mesh

2 消声器声学性能分析

2.1 传递损失理论

传递损失是表示声音经过消声元件后声音能量的衰减,亦称传声损失或者消声器的隔声量,它是评价消声元件的最简单方法和重要指标.传递损失没有包括声源和管道终结端的声学特性,它只与自身的结构有关.当某个声学元件的结构确定了,那么传递损失也就确定了,而且传递损失与消声元件在一个系统中的位置没有关系,只取决于消声元件的结构、介质的阻抗率和截面面积.

传递损失为消声元件入口处的入射声功率级LWi和出口处的透射声功率级LWt之差,其可用TL(Transmission Loss)表示:

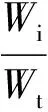
(5)

在汽车进、排气管道所涉及的频率范围内,声波的波长远远大于这些管道的直径,消声器入口和出口的截面通常都不大,声波在其中主要是以平面波的形式进行传播.声波在管道中传播,当达到管道顶端的时候,一部分声波会透过管道继续传播,而另一部分声波则会反射回去,形成反射波,如图4.

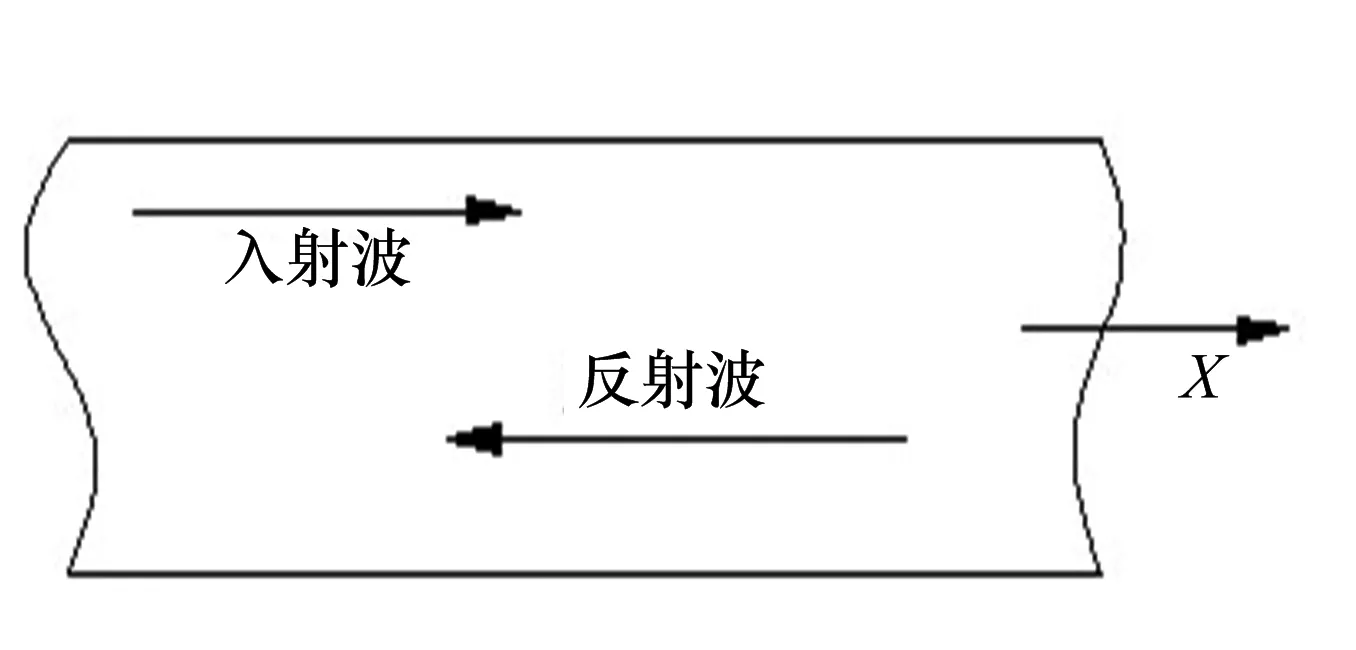
图4 管道中的声波Fig.4 Sound wave in pipe

在这些小截面管道中,声波方程简化为一维波动方程[7]:

(6)

入射波的声压pi和声速ui分别为:

pi(x,t)=Piej(ωt-kx)

(7)

ui(x,t)=umiej(ωt-kx)

(8)

式中:Pi和umi分别为入射声波声压幅值和速度幅值;k和ω分别是声波的波数和角频率.

反射波的声压pr和速度ur分别为:

pr(x,t)=Prej(ωt+kx)

(9)

ur(x,t)=umrej(ωt+kx)

(10)

式中:Pr和umr分别为反射声波声压幅值和速度幅值.

管道中任何一点的声压是入射声压和反射声压的合成,或者说是方程(6)的解,p=p(x,t),可以写成:

p(x,t)=Piej(ωt-kx)+Prej(ωt+kx)

(11)

由于入射波和反射波的速度方向相反,所以合成声速为:

u(x,t)=umiej(ωt-kx)-umrej(ωt+kx)

(12)

声压和速度之间存在下列关系:

(13)

式中:z是声阻抗率.对于自由声场的平面波,声阻抗率就变成了特性阻抗z0=ρc.

2.2 定义入口单位质点振速的方法计算传递损失

图5为消声器的传递损失理论模型.

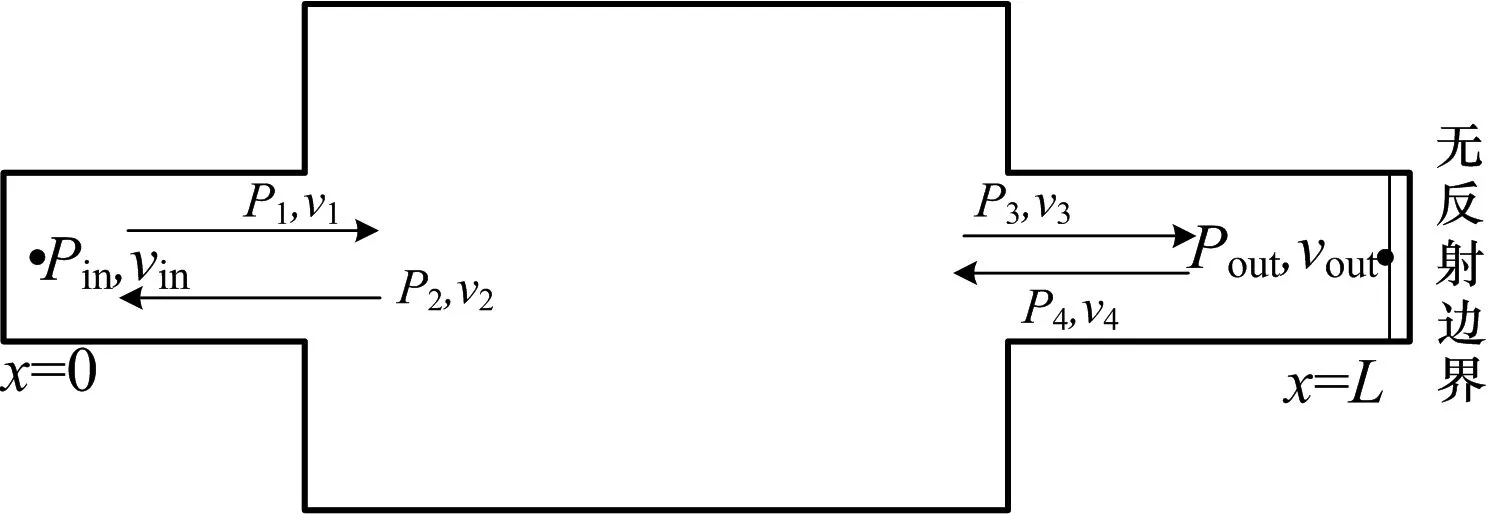
图5 消声器传递损失理论模型Fig.5 Transmission loss model of muffler

由上面管道声学理论,可得在x=0处入射声压p1和入口声压pin的关系:

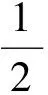
(14)

在x=L处由于定义了无反射边界条件,所以出口的反射声压p4=0,可得出口的透射声压

p3=pout

(15)

根据传递损失的定义及声压和声功率之间的关系,就可以得到传递损失的计算公式:

(16)

式中:Ain为消声器入口截面积,Aout为消声器出口截面积,这里出口和入口截面积相等,即有Ain=Aout.在声学计算中,声压p都是复数.

传递损失是消声器的固有属性,所以可以通过在消声器入口添加单位振动速度来计算出口处的声压响应从而得到传递损失.整个消声器为刚性壁管组成,所以声波不会由管壁透出,只会在管壁位置发生完全反射.出口位置会使声波透出,为代表出口与外界大气相通可以将出口位置的阻抗设为与大气阻抗相同.一般计算消声器的传递损失,需要设定以下3个边界条件:

1) 入口边界条件 入射波为平面波,在入口处施加单位振动速度,vn=-1m·s-1.

2)出口边界条件 在出口处施加无反射边界条件,即在出口处定义声阻抗Zp=ρc.

3)内壁面边界条件 不考虑壁面吸收,认为壁面是刚性壁面,在刚性壁面上介质的法向振动速度为零.

经过以上的前处理后,在Virtual.lab中计算入口处振动速度引起的消声器内部声压分布.图6，7分别是消声器在100，2900Hz时的内部声压分布.

从图6可以看出当在100Hz低频时无论在出入口管和内插管还是扩张室都是以平面波传播,各个截面的声压值相等.而在高频范围内,如图7在2900Hz时,扩张室内已不再是平面波,而是出现了高次波,且声波在壁面的反射效应强烈,各截面的声压值不再相等,此时一维声学已不再适用,不能再用一维平面波理论的计算方法进行设计，但是可以看出，出入管和内插管由于截面积比较小,其内部声波依然是平面波.

在计算消声器传递损失时,需在入口和出口面上定义输入和输出点,得到出入口点的声压响应函数，如图8(实线为入口点声压响应,虚线为出口点声压响应).然后根据消声器传递损失理论,由式(16)即可得到传递损失,如图9.

图6 消声器内部100 Hz的声压分布Fig.6 Sound pressure distribution in muffler(100 Hz)

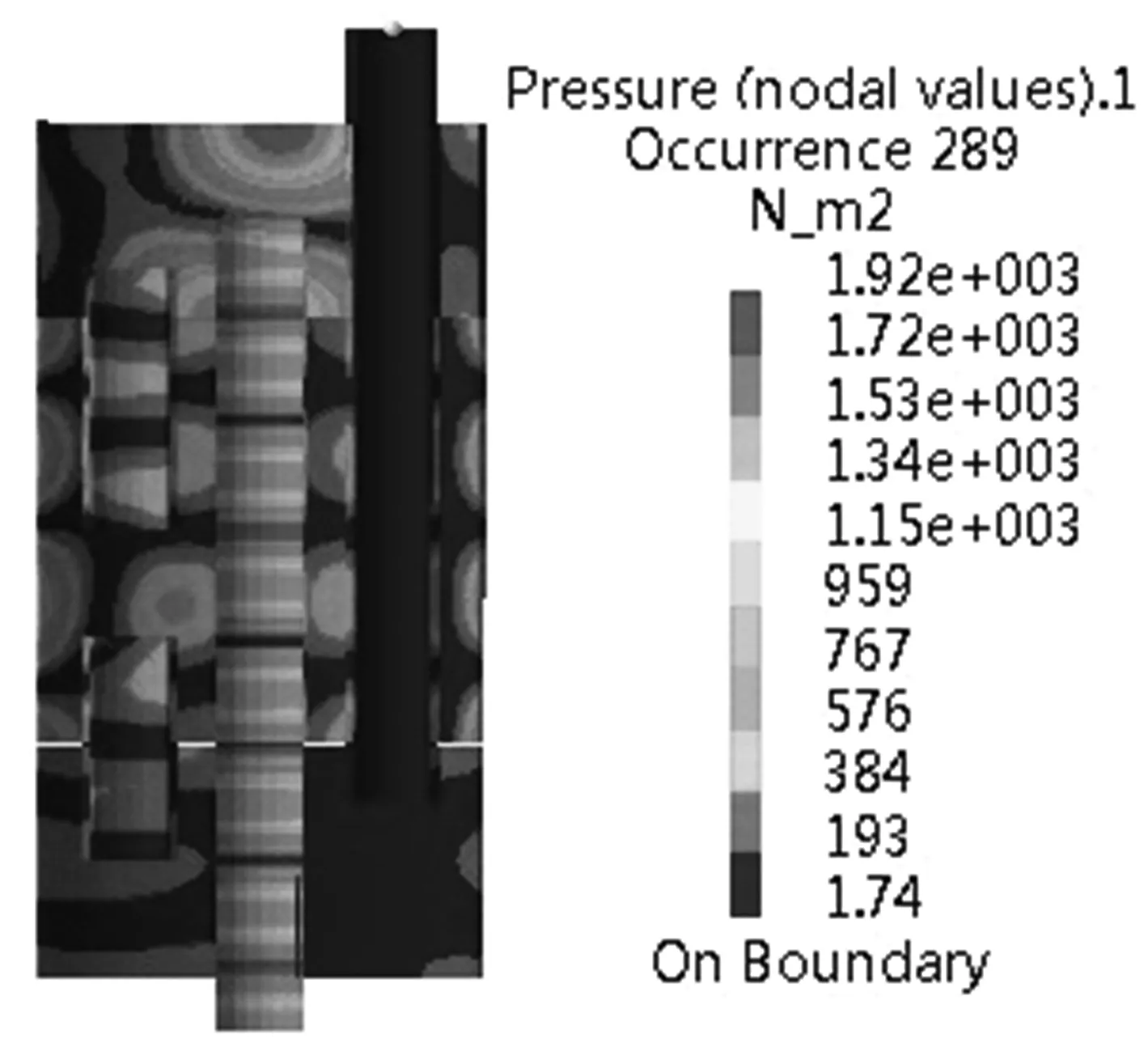
图7 消声器内部2 900 Hz的声压分布Fig.7 Sound pressure distribution in muffler(2 900 Hz)

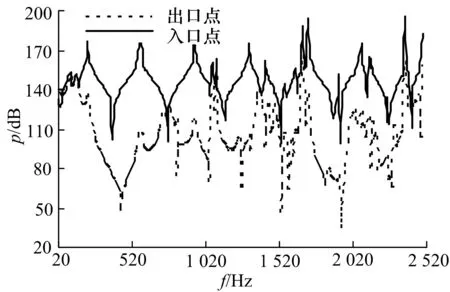
图8 出入口声压频率响应函数Fig.8 Sound pressure frequency response functionon inlet and outlet

图9 第一种方法计算出的传递损失Fig.9 Curve of transmission loss with first method

2.3 利用AML技术直接定义声功率的方法计算传递损失

AML动匹配辐射边界条件是LMS Virtual.Lab的新技术.这种方法不需要添加人工声学吸收层网格,只要画出声学有限元声辐射边界条件,就会自动定义吸收层和吸收系数.这样就能提高计算精度(由于人为划分吸收层网格造成),减少工作量,也提高计算速度.AML除了在计算外场噪声方面更方便外,在管道声学方面也有很多应用.图10为AML方法定义管道无反射边界条件示意图.

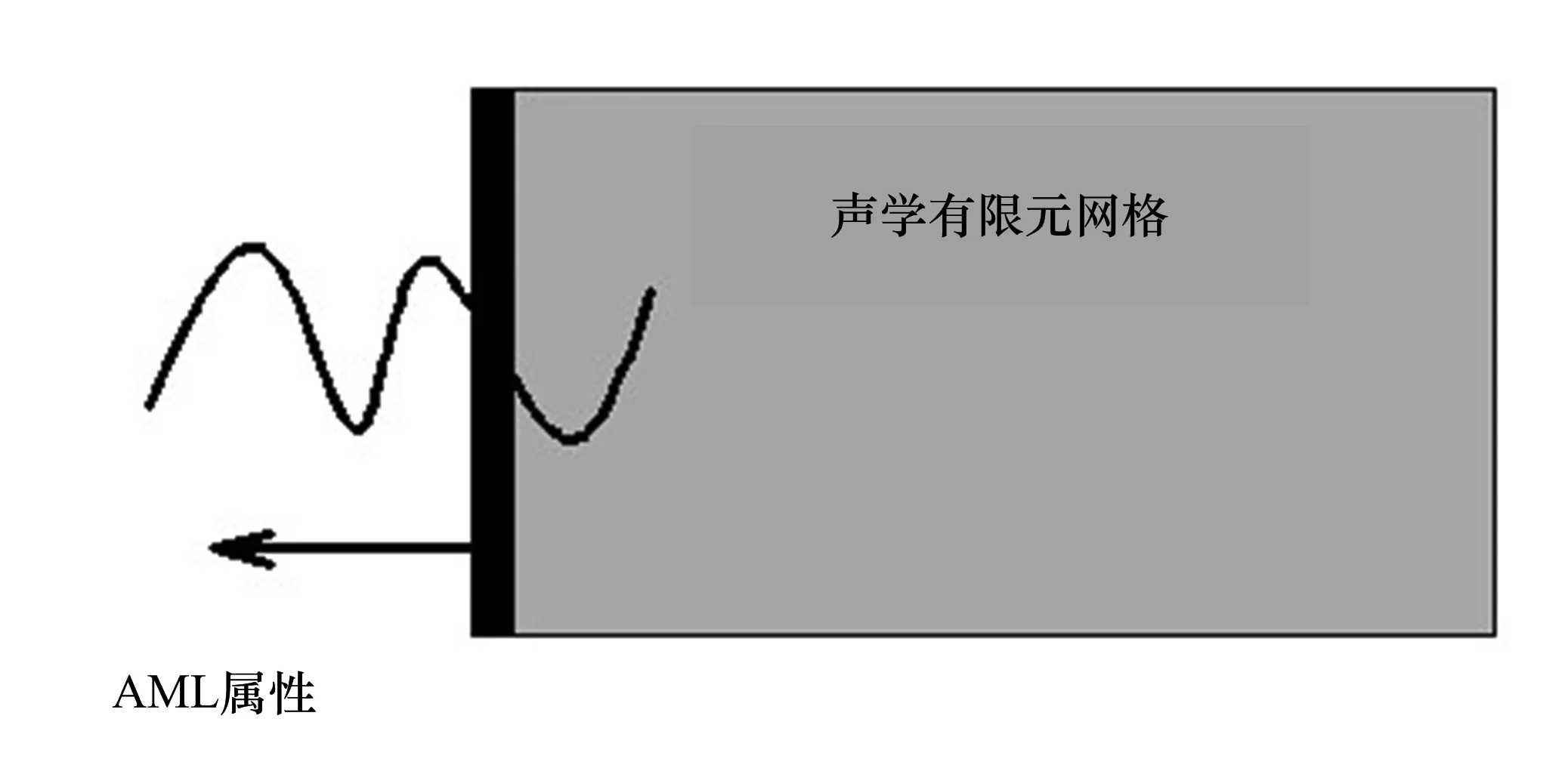
图10 AML方法定义管道无反射边界Fig.10 Anechoic end duct boundary with AML method

用AML方法不需要再去离散部分声学网格作为吸收层,只需要直接在管道出口边界定义AML属性,就可以实现无反射边界条件.

由于消声器的传递损失和声源特性无关,所以可以直接在入口定义延x轴直线传播的(0,1)阶管道声模态,并且赋予1W的声功率,在LMS VL中,(0,1)阶管道声模态即为平面波,其声压方程为:

p01=P01ej(ωt-kx)

(17)

式中:P01为(0,1)阶波声压幅值.

在出口定义AML无反射边界条件,AML就会自动计算出口声功率,直接得到传递损失.图11为计算的出口声功率,图12为计算出的传递损失.

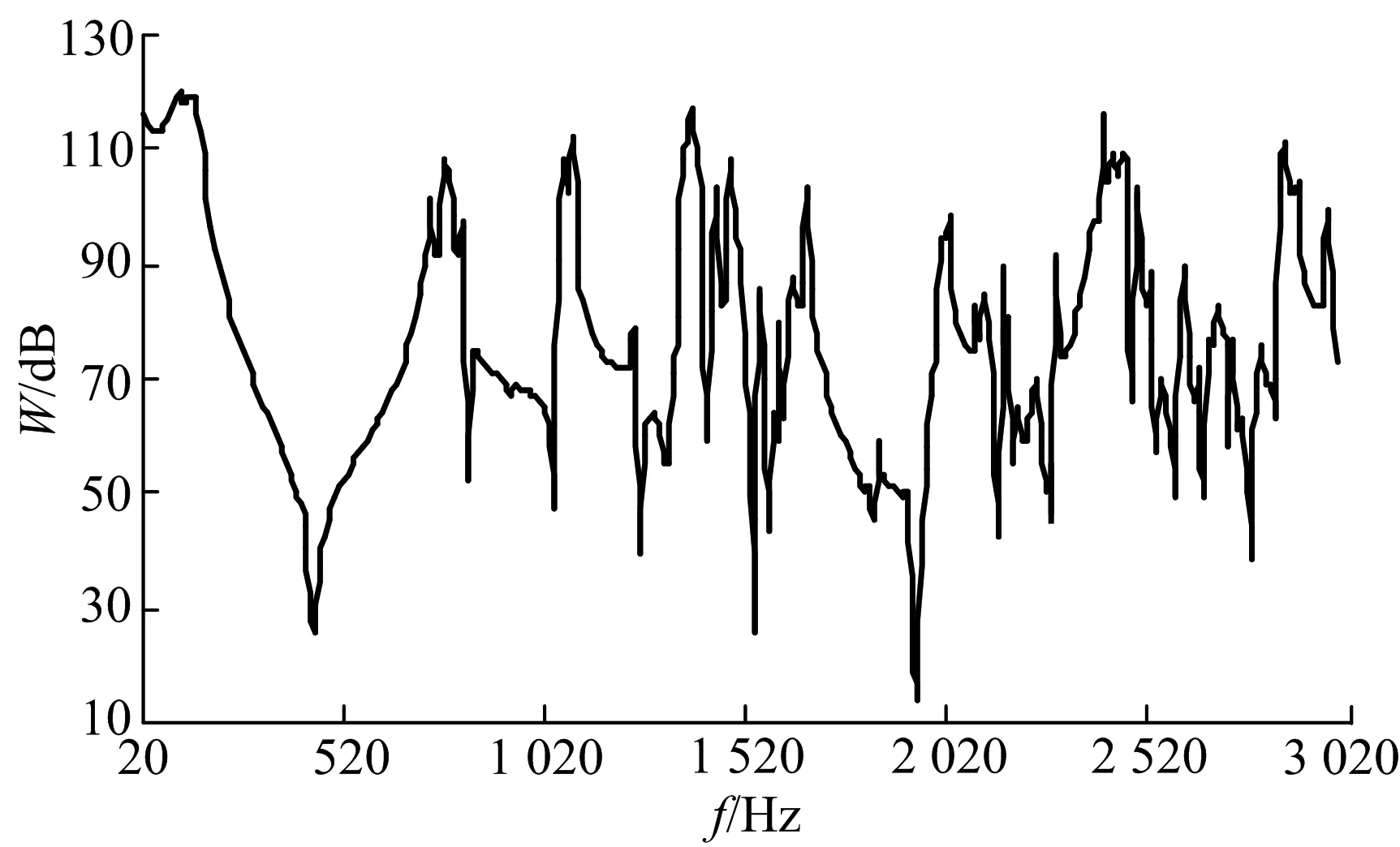
图11 消声器出口的声功率频率响应函数Fig.11 Sound power frequency responsefunction on outlet of muffler

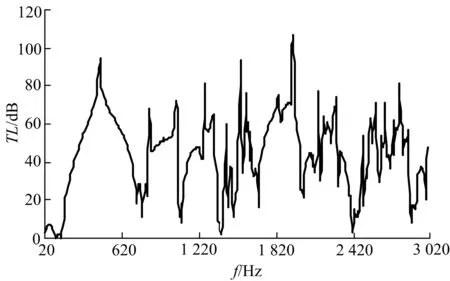
图12 第2种方法计算出的传递损失Fig.12 Curve of transmission loss with second method

通过对传递损失的结果进行分析,这两种方法计算出来的结果高度一致.在110Hz时有最小消声量0.233dB;在1950Hz时有最大的消声量106.485dB.第1种方法首先计算出消声器出入口的声压响应,然后需要通过管道声学理论分离出入口的入射声波和反射声波,最后通过声功率和声压的关系才计算得到其传递损失.而第2种方法直接定义声功率计算传递损失,计算步骤简单、计算速度提高40%左右.

特别对于大截面管路消声器,在出口边界上,传统的空气特性阻抗边界不再适用;声源上,也无法采用平面波进行模拟.而第2种方法不仅适合小截面的管道,而且在大截面管路消声器也同样适用.当入口不再只是平面波时,可以定义其他模态的高次波;在出口边界,可以定义AML属性来代替特性阻抗边界条件.

3 消声器出口辐射噪声的研究

消声器出口的辐射噪声不仅可以反映排气尾管的声学特性,同时也为研究插入损失提供一种仿真方法.

根据内燃机排气消声器测量方法,考虑到气流速度的影响,一般测量点为排气口和排气气流成45°方向,距离排气口500mm.为此以消声器出口为圆心,建立半径为500mm的1/4半球的场点网格,在出口45°的场点网格上取一个IO点作为测量点,如图13.

图13 消声器出口场点网格Fig.13 Field point mesh for outlet of muffler

考虑气流速度的影响,在入口处施加60m/s的流速和1W的声功率,出口出施加AML全透边界条件,即声音传到出口的壁面上,直接传播到大气中.经过计算得到了出口的辐射噪声.图14为场点网格在流速为60m/s，1800Hz的声压云图.

图14 场点1 800 Hz的声压云图Fig.14 Sound pressure on field point mesh

为了反映出整个频率范围内的声压响应,选取场点网格的IO点作为输出点,经过计算得到这个输出点的声压频率响应函数,如图15.

图15 IO点声压频率响应函数Fig.15 IO point sound pressure frequencyresponse function

插入损失一般定义为:装置消声器前后,声源通过排气口向外辐射噪声的声功率级之差.插入损失用IL(insertion loss)表示

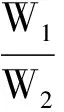
(18)

式中:W1是没有安装消声元件的系统在测量点的声功率;W2是安装了消声元件后在同一点测量的声功率.

与传递损失只考虑消声元件本身不同,插入损失是考虑整个排气系统.也就是除了消声元件外,插入损失还包括了声源和出声口(进气口和排气尾管)的声学特征,所以插入损失相比传递损失更能反映排气消声器的声学性能.

插入损失边界条件需要在入口处加载发动机排气噪声频谱和排气端阻抗边界[6].出口需要考虑尾管效应,管道内的声波要通过管口不断的向周围空间辐射.如图16是建立的插入损失有限元计算模型,该模型的关键是在出口处设计建立一个模拟无穷远的有限元声场,可以在出口管端面定义AML属性便能模拟这种声场特性,从而使消声器的出口阻抗和实际情况一样,并且按照《GB/T 4759-2009内燃机排气消声器测量方法》[8],在出口500mm，45°定义辐射场点的声功率级或者声压级来获取直管和带消声器时的尾管噪声,两者的差值便是插入损失.

图16 插入损失有限元模型Fig.16 FEM modal of insert loss

仿真分析完毕后,通过出入口的位置读取相应节点的数据,并通过4点法[9-10]计算尾管噪声结果(插入损失).

4 结论

文中利用声学有限元理论,对某车消声器的声学性能进行了分析研究,得到了如下结论:

1)用三维声波波动方程的有限元计算方法,在Virtual.Lab Acoustics中仿真消声器的声学性能,相比传统的基于一维平面波理论的研究方法,计算更加准确,研发周期短,而且可以精确模拟消声器的高频特性.

2)采用定义入口单位质点振速的方法,分析了消声器内部声压分布特性,得到了出入口声压响应,为进一步研究消声器内部声学性能提供了一定的依据.

3)采用AML技术直接计算声功率的方法得到消声器的传递损失,并且和第1种方法相比,计算结果高度一致,两者在110Hz时有最小消声量0.233dB;在1950Hz时有最大的消声量106.485dB.但第2种方法步骤简单,且对于大截面管路消声器也同样适用,显示了其计算方法的优越性,为大截面管路消声器传递损失计算提供了一种新方法.

4)利用第2种方法研究分析考虑气流速度影响的消声器出口的辐射噪声,得到了出口场点网格上IO点声压(dB)的频率响应函数,并且建立了消声器插入损失的有限元计算模型,为研究插入损失的研究提供了一种仿真方法.

References)

[1] 马家义,袁兆成.汽车排气消声器传递损失试验方法的研究[J].噪声与振动控制,2009,29(6):161-164. Ma Jiayi, Yuan Zhaocheng.Study on test method of transmission loss of vehicle muffler[J].NoiseandVibrationControl,2009,29(6):161-164.(in Chinese)

[2] Munjal M L. Acoustics of ducts and mufflers with application to exhaust and ventilation system design [M].New York: Wiley-Interseience, 1987.

[3] 杨俊智,马晓光.排气消声器的设计及性能仿真分析[J]. 机械设计与制造,2011,247(9):106-108. Yang Junzhi, Ma Xiaoguang. Design and performance simulation analysis for exhaust muffler[J].MachineryDesign&Manufacture,2011,247(9):106-108. (in Chinese)

[4] 葛蕴珊,张宏波.汽车排气消声器的三维声学性能分析[J].汽车工程,2006,28(1):51-55. Ge Yunshan, Zhang Hongbo. An analysis on 3D acoustic performance of automotive exhaust muffler[J].AutomotiveEngineering,2006,28(1):51-55. (in Chinese)

[5] 袁兆成,丁万龙.排气消声器的边界元仿真设计[J].吉林大学学报,2004,34(7):357-361. Yuan Zhaocheng, Ding Wanlong. Simulation analysis of exhaust muffler with boundary element method[J].JournalofJilinUniversity,2004,34(7):357-361. (in Chinese)

[6] 李沛然.汽车排气消声器设计技术研究及其专家系统开发[D].重庆:重庆大学,2011.

[7] 庞剑,湛刚,何华.汽车噪声与振动:理论与应用[M].北京:高等教育出版社,2006.

[8] 中国机械工业联合会.GB/T4759-2009内燃机排气消声器测量方法[S].北京:中国标准出版社, 2009.

[9] ASTM.ASTM E2611-09Standard test method for measurement of normal incidence sound transmission of acoustical materials based on the transfer matrix method[S]. West Conshohocken, PA: ASTM International, 2009.

[10] 王国治, 胡玉超. 舰船结构声学设计及噪声预报技术探讨[J].江苏科技大学学报:自然科学版, 2012, 26(4): 327-331. Wang Guozhi, Hu Yuchao. Research on acoustic design of warship structure and prediction of underwater noise[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2012, 26(4): 327-331. (in Chinese)

(责任编辑：顾 琳)

Researchonacousticperformancepimulationofautomotiveexhaustmufflers

Wang Xinyan1，Tang Bo1，Yuan Chunyuan1，Qiu Zhonghua2

(1.School of Mechanical Engineering,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)(2.Joint Logistics Department,Nanjing Military Area Command,Nanjing Jiangsu 210016,China)

This paper presents two different methods for the study of transmission loss of mufflers based on three-dimensional acoustic wave equation using the finite element software LMS.Virtual Lab Acoustics. The first method used defined unit velocity of particle vibration on the inlet; another method used technology of AML to calculate sound power. The results show that the calculation results of the two methods are highly consistent. The second method has simpler calculation steps and faster calculation speed and it is suitable for the large cross-section duct muffler; Compared with the traditional transfer matrix method and the empirical method,the calculation speed has been improved by using the three-dimension acoustic finite element method, and the transfer error of muffler based on one-dimensional plane waves has been effectively reduced. Finally, the radiation noise of muffler outlet was studied in the second method based on the effect of flow velocity, and the finite element calculation model of insertion loss was also established.

transmission loss;sound pressure;sound power;radiation noise;insertion loss

10.3969/j.issn.1673-4807.2014.04.010

2014-04-02

江苏省科技厅成果转化专项基金资助项目(BA2009)

王新彦(1962—),女,博士,副教授,研究方向为汽车动力学及汽车振动噪声.E-mail:xinyan@just.edu.cn

U469.5+41

A

1673-4807(2014)04-0351-07