掺钌硅原子簇的结构及其稳定性研究
刘 源, 李国良, 陈红雨, 李前树
(华南师范大学化学与环境学院,环境理论化学省部共建教育部重点实验室,广州市能源转化与储能材料重点实验室,广州 510006)
硅原子簇在微电子工业、能源材料和催化剂等领域有着广泛的应用,吸引着人们的广泛注意[1-2]. 碳原子在成簇时易采用sp2杂化乃至sp杂化形式,通过其自身原子间的共价多重键(σ键+π键)形成直线链状、平面环状或富勒烯笼状结构,与碳原子成族过程不同,硅原子在成簇时多采用sp3杂化形式以共价单键(σ键)相结合,形成紧密的、高价的三维结构[3-4]. 由于大量未成对电子及悬键的存在等因素,纯硅原子簇的结合能低,化学活性高,不易稳定存在. 把过渡金属原子掺入到硅原子簇,饱和了原子簇的未成对电子及悬键,提高其稳定性.这些原子簇还有可能产生新的性质. 1989年,Beck[5]用激光蒸发技术合成了小的TM@Sin(TM=Cr, Mo, W, 等)原子簇,发现在相同的尺寸下,掺杂金属原子的硅原子簇比纯硅原子簇有着更高的稳定性. 从此,实验和理论上对过渡金属掺杂的硅原子簇的研究越来越广泛[3-4,6-9].掺杂过渡金属原子确实能提高硅原子簇的稳定性,而且随着原子簇尺寸的增大,过渡金属原子趋向于进入硅笼中.
钌硅化合物在发光二极管等基于硅的光学应用中有着广阔的前景[10]. 对掺钌硅化合物的研究有助于提高人们对钌硅化合物的认识. Lindholm 和 Morse[11]首次报道了双原子钌硅化合物RuSi的气相光谱研究,显示基态RuSi的电子态为3Δ,电子组态为2δ314σ1. Gueorguiev 和 Pacheco[12]计算了TMSin(TM=Cr, Mo, W, Mn, Tc, Re, Fe, Ru, Os, Co, Rh, Ir)原子簇,发现这些原子簇的结合能随着尺寸的增大有着相似的变化趋势,当n=7,12时,都有着相对较大的结合能. 本文对RuSin(n=1~14)原子簇的结构、稳定性和增长趋势等进行了系统的研究,希望这些结果能对今后有关掺钌硅原子簇的质谱和光电子能谱等研究提供指导和帮助.
1 计算方法
本文采用密度泛函理论中的B3LYP方法进行计算,其中B3是Becke 的三参数交换势能函数[13],LYP是Lee、Yang和Parr的相关势能函数[14]. 该法已被成功用于掺杂的硅原子簇的计算研究[15-17].
由于重原子含有较多的电子,并且有较严重的相对论效应,因此对含重原子体系的理论计算相对较为困难. 为了减少计算量,一种常用的解决办法就是使用相对论有效核势(RECPs)及其相关基组:将重原子的化学惰性的内层电子的影响用RECPs取代,在计算时只计算价层电子的作用. 本文使用SDD[18]和LanL2DZ[19]两种RECPs及其相关基组,它们都用势函数取代了Ru原子的内部1s22s22p63s23p63d10电子的影响,计算时只考虑Ru原子的价层4s24p64d75s电子.
最初考虑4种基组:(1)SDD6311,对Ru原子用SDD势及其相关基组,对Si原子用6-311+G*基组;(2)LanL2DZ6311, 对Ru原子用LanL2DZ势及其相关基组,对Si原子用6-311+G*基组;(3)SDD,对Ru和Si原子都用SDD势及其相关基组;(4)LanL2DZ,对Ru和Si原子都用LanL2DZ势及其相关基组. 用B3LYP方法结合这4种基组分别计算RuSi的键长、解离能和电子态(表1). 与实验结果进行比较,发现用SDD6311基组计算的结果与实验值最接近. 为了进一步验证SDD6311基组对该计算体系的可靠性,采用此基组计算Si原子和Ru原子的电离势(IP)和电子亲合势(EA),结果为IP(Si)=8.11 eV,EA(Si)=1.33 eV,IP(Ru)=7.68 eV,EA(Ru)=1.09 eV, 与实验值IP(Si)=8.15 eV,EA(Si)=1.39 eV,IP(Ru)=7.36 eV,EA(Ru)=1.05 eV[20-21]非常接近;计算出Si2中Si-Si键长和键能,分别为0.228 0 nm和3.36 eV,与实验值0.228 0 nm和3.21 eV[22]也很接近;计算出Ru2中Ru-Ru键的键长和键能分别为0.227 nm和2.56 eV,与实验和其它理论结果[23-24]也相吻合. 因此,本文选用SDD6311基组.
表1用B3LYP方法结合6311SDD、6311LanL2DZ、SDD和LanL2DZ四种基组得到RuSi基态结构的键长、解离能和电子态
Table 1 Bond length, dissociation energy and electronic state for the ground state of the RuSi dimer at the B3LYP level with the 6311SDD, 6311LanL2DZ, SDD, LanL2DZ basis sets
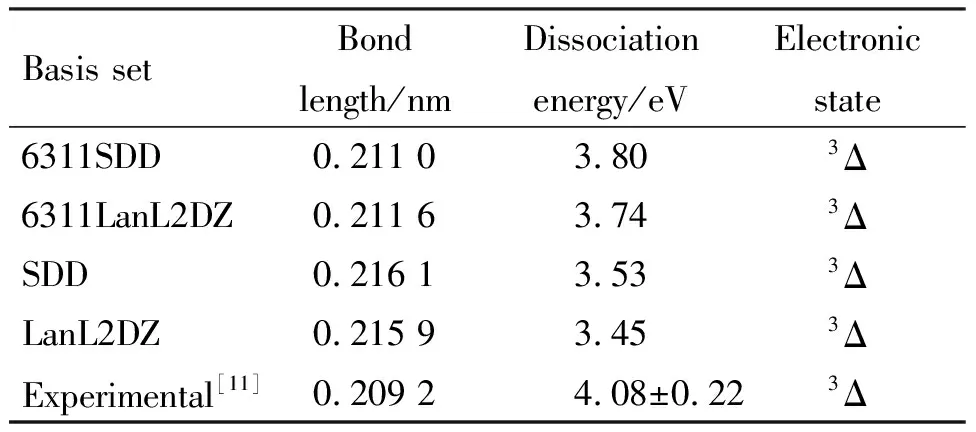
Basis setBond length/nmDissociation energy/eVElectronic state6311SDD0.211 03.803Δ6311LanL2DZ0.211 63.743ΔSDD0.216 13.533ΔLanL2DZ0.215 93.453ΔExperimental[11]0.209 24.08±0.223Δ
为了判断各稳定点(优化结构)的性质,采用B3LYP/6311SDD方法计算其振动频率. 如有虚频出现,则沿着虚频的振动方向修改坐标,直到找到真正的极小点. 除了结构和能量分析,本文还进行了自然键轨道(NBO)分析. 所有的计算均采用Gaussian 03[25]软件包进行.
2 结果与讨论
为了得到RuSin(n=1~14)原子簇的最稳定结构,设计初始结构如下:(1)把Sin+1原子簇基态结构[26]中的一个Si原子用Ru原子取代;(2)把Ru原子加到Sin原子簇基态结构[26]的不同面上;(3)把Si原子加到RuSin-1原子簇基态结构的不同面上;(4)参考其它掺杂硅原子簇的基态结构. 对于同一个结构,我们考虑单态、三态和五态3个电子态.
2.1 RuSin (n=1~14)的稳定结构
(1)n=1.图1为RuSin(n=1~5)原子簇的低能量结构,深色球表示Ru原子,浅色球表示Si原子. 在每个结构图下,标出了其对称性、电子态及相对能量. 对各结构的命名iN-j,i表示Si原子的个数n;N表示中性原子簇;j=1表示基态结构,j=2,3,4,…表示第二、三、四等稳定结构. 双原子分子RuSi的基态1N-1呈三态3Δ(电子组态为2δ314σ1). 相应的单态和五态的能量分别比三态的高22.1和23.7 kcal/mol. 尽管Ru原子半径大于Fe原子,但RuSi的基态结构中的Ru-Si键长为0.211 0 nm,比FeSi的短了0.006 2 nm[27],说明Ru和Si的结合力比Fe和Si的更强. 根据本文计算,Ru和Si的结合能(43.86 kcal/mol),比Fe和Si的结合能大19.45 kcal/mol[27]. 文献报道MnSi与TcSi、CoSi与RhSi[28]也存在类似的结果. NBO分析显示,RuSi存在很强的dπ-pπ键,与实验结果吻合[11].
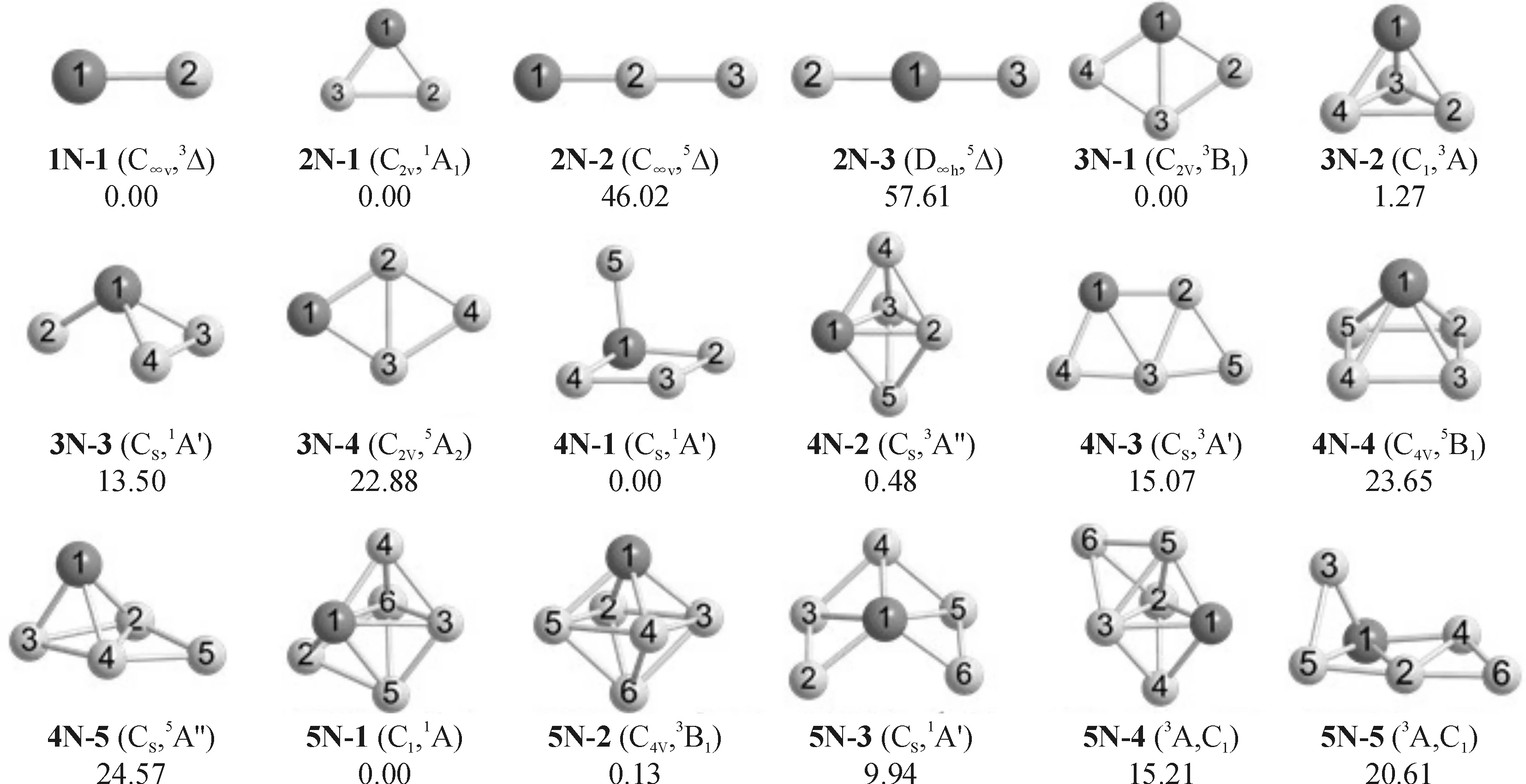
图1 RuSin (n=1~5)原子簇的低能量结构
(2)n=2.与FeSi2相似[27],RuSi2的基态结构2N-1(图1)呈C2v对称(等腰三角形),可由Si3的基态结构[26]用Ru原子代替其中的1个Si原子得到.2N-1结构的电子态为1A1;Si-Si键长为0.251 3 nm,比FeSi2中的Si-Si键长短0.026 0 nm;Ru-Si键长为0.214 0 nm,比FeSi2中的Fe-Si键长短0.016 3 nm[27]. NBO分析表明,2N-1中有一个三中心键,这有利于该结构的稳定性. Ru在一端(2N-2)或Ru在中间(2N-3)的线型结构都有相对较高的能量.
(3)n=3.对RuSi3,Ru原子位于短对角线上的菱形结构3N-1(图1)为基态结构,具有C2v对称性和3B1电子态. 相应单态结构的能量比3N-1高3.53 kcal/mol. Qin[26]等报道了纯硅原子簇Si4的基态结构也为平面菱形结构. NBO分析显示,3N-1中2个三中心键分布于Ru1-Si2-Si3 和Si2-Si3-Si4之间. 三角锥结构3N-2具有3A电子态,能量比3N-1高1.27 kcal/mol. 第三稳定结构3N-3为压扁的三角锥结构,其能量比3N-1高13.50 kcal/mol. 异构体3N-4也为菱形结构,Ru原子位于长对角线上,其能量比3N-1高22.88 kcal/mol.
(4)n=4.RuSi4的基态结构4N-1(图1)可视为1个Si原子接到3N-1的Ru原子上形成的,Si5-Ru-Si3键角为101°.4N-1结构具有Cs对称性和1A′电子态. NBO分析显示,4N-1中在Si2-Si3-Si4之间有1个三中心键,有利于其稳定存在. Ru原子位于赤道位置的三角双锥结构4N-2为RuSi4的次稳定结构.4N-2结构具有Cs对称性和3A″电子态,能量比4N-1高0.48 kcal/mol,也是RuSi4基态结构的候选者. 第三稳定结构4N-3为梯形结构,可看作是在3N-1的Si2-Si3边上加1个Si原子形成的,能量比基态高15.07 kcal/mol. 四角锥结构4N-4具有C4v对称性和5B1电子态. 把Ru原子戴在Si4菱形结构的1个三角面上就得到4N-5结构.4N-4和4N-5结构的能量都较高,分别比4N-1的高23.65和24.57 kcal/mol.
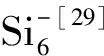
(6)n=6.RuSi6原子簇的5个低能量结构(图2)中,能量最低的6N-1结构为五角双锥结构,Ru原子位于轴上,具有C5v对称性和1A1电子态. NBO分析显示,在6N-1中有4个三中心键,分布于Si2-Si5-Si7, Si2-Si6-Si7 和Si3-Si4-Si5之间. Si7[26]的最稳定结构也是此类构型. 能量次低的6N-2结构具有C3v对称性和1A1电子态,可看作为5N-3结构的衍生结构,能量比6N-1高3.02 kcal/mol. 接下来的2个能量较低结构6N-3和6N-4都是Si戴帽的四角双锥结构,Ru原子位于轴向位置. 前者具有Cs对称性和3A″电子态,后者具有Cs对称性和1A′电子态,能量分别比6N-1高3.08 和3.54 kcal/mol.6N-5结构可视为边戴帽的三棱柱,能量比6N-1高7.04 kcal/mol.
(7)n=7.RuSi7原子簇的低能量结构多为戴帽的双锥结构(7N-1,7N-3~7N-5,图2). 双戴帽的四角双锥结构7N-1为基态结构,它可视为在6N-4的Si2-Si5-Si6面上戴1个Si原子形成的.7N-1结构具有Cs对称性和3A′电子态. NBO分析显示,在7N-1结构中有7个三中心键,分布于Ru1-Si5-Si8, Si2-Si3-Si7, Si2-Si5-Si8, Si2-Si6-Si8, Si3-Si6-Si8, Si4-Si5-Si6, Si4-Si5-Si7之间. 该结构与Si8[29]的基态结构相似. 变形的立方体结构7N-2具有Cs对称性和1A′电子态,能量比基态结构高9.16 kcal/mol. 边戴帽的五角双锥结构7N-3可视为在6N-1的Si5-Si6边上戴帽1个Si原子形成,其能量比7N-1高9.26 kcal/mol. 把2个Si原子分别戴在5N-4的Ru1-Si2-Si4面和Ru1-Si3-Si4面上,得到RuSi7的第四稳定结构7N-4. 该结构具有1A′电子态,能量比基态高12.24 kcal/mol.7N-5结构为另一个双戴帽的四角双锥结构,其能量比7N-1高17.57 kcal/mol.
(8)n=8.对RuSi8,能量最低的结构8N-1(图2)具有Cs对称性和1A′电子态,可视为在7N-1的Ru1-Si8边上戴1个Si原子形成.8N-1结构与Si9[26]、FeSi8[27]的基态结构具有很大的不同,Si9的基态结构为戴帽的不规则四棱柱,而FeSi8的基态结构由两个四角双锥共面形成.8N-1中有5个三中心键,分布于Ru1-Si3-Si7, Ru1-Si4-Si7, Si2-Si3-Si7, Si2-Si5-Si8,Si4-Si5-Si7之间. 次稳定结构8N-2可视为在7N-2的Ru原子上戴1个Si原子形成的,其能量比8N-1的仅高1.99 kcal/mol.8N-3和8N-5都是戴帽的五角双锥结构,能量分别比8N-1高5.30和17.16 kcal/mol. 三戴帽的四角双锥结构8N-4可视为1个Si原子戴在7N-5的Si3-Si7-Si8面上形成,具有Cs对称性和1A′电子态,其能量比8N-1高15.37 kcal/mol.
(9)n=9.把1个Si原子戴在RuSi8的基态结构8N-1上,得到RuSi9的最稳定结构9N-1(图2),其具有Cs对称性和1A′电子态.9N-1结构与Si10[26]和FeSi9[27]的最稳定结构不同. NBO分析发现,在9N-1中有4个三中心键,分布于Si2-Si3-Si8, Si3-Si7-Si9, Si4-Si5-Si8 和Si4-Si7-Si9之间. 次稳定结构9N-2可视为1个半包围的笼状结构,Ru原子陷入了Si3-Si4-Si8-Si9菱形环和Si2-Si5-Si6-Si7-Si10五元环之间.9N-2结构具有Cs对称性,能量比9N-1高12.08 kcal/mol.9N-3和9N-4的构型不同,但它们的能量很接近,分别比基态高17.69和17.83 kcal/mol. 将1个Si原子戴在8N-5的Ru1-Si5边上得到结构9N-5,其具有Cs对称性和1A′电子态,能量比基态高18.33 kcal/mol.
(10)n=10.由RuSi9的次稳定结构9N-2边戴帽1个Si原子,得到RuSi10的最稳定结构10N-1(图3).10N-1结构具有Cs对称性和1A′电子态. NBO分析显示,在10N-1中有8个三中心键,分布于Ru1-Si7-Si10, Si2-Si3-Si9, Si2-Si5-Si6, Si3-Si4-Si5, Si4-Si8-Si9, Si6-Si10-Si11, Si7-Si8-Si9和Si7-Si10-Si11之间.10N-2结构是8N-2的衍生结构,能量比10N-1高5.07 kcal/mol. 异构体10N-3呈半封闭结构,Ru原子趋向于插入Si10笼中,具有Cs对称性和1A′电子态,能量比10N-1高9.60 kcal/mol.
图2 RuSin (n=6~9)原子簇的低能量结构
(11)n=11.RuSi11的基态结构11N-1呈塔状(图3),具有C3v对称性和1A1电子态. 基于NBO分析,11N-1中有3个三中心键,分布于Si6-Si7-Si9, Si6-Si9-Si12 和Si7-Si9-Si12之间.11N-2结构可视为边戴帽的五棱柱结构,Ru原子靠近Si2-Si3-Si4-Si6-Si7面,其能量比11N-1高3.06 kcal/mol.11N-3结构是1个扭曲的长方体结构,具有Cs对称性和1A′电子态,能量比11N-1高4.10 kcal/mol.
(12)n=12.当n≥12时, RuSin原子簇最稳定的结构呈现笼状结构, Ru原子完全陷入Sin笼内. RuSi12最稳定的结构为D6h对称性的六棱柱结构,具有1A1g对称性. Guo等报道过渡金属Ti、V、Cr和Cu也陷入Si12笼中间,形成六棱柱结构[30]. NBO分析显示,12N-1中有9个三中心键,分布于Ru1-Si3-Si7, Ru1-Si4-Si8, Ru1-Si5-Si12, Ru1-Si6-Si10和Ru1-Si9-Si11之间(图4),原子编号见图3中的结构12N-1, 这些三中心键有利于该结构的高稳定性.12N-2结构可看作为1个Si2二聚体戴在扭曲的五棱柱的1条边上形成的,具有D2d对称性和3A1电子态,其能量比12N-1高7.01 kcal/mol.12N-3结构可看成是11N-1的衍生物,具有Cs对称性和1A′电子态,能量比12N-1高19.90 kcal/mol.
(13)n=13.RuSi13的最稳定结构13N-1(图3)是12N-2的衍生结构,视为由Si原子戴在其Si4-Si8边上形成.13N-1结构具有Cs对称性和1A′电子态. 次稳定结构13N-2为笼状结构,Ru原子位于笼中,具有C2v对称性和1A1电子态,能量比13N-1高4.04 kcal/mol. 另一稳定结构13N-3是1个Si原子面戴帽的扭曲六棱柱,能量比13N-1高13.00 kcal/mol.
(14)n=14.RuSi14的基态结构14N-1(图3)是13N-1的衍生结构,可视为1个Si原子戴在13N-1的Si6-Si12边上形成的.14N-1结构具有Cs对称性和1A′电子态. 次稳定结构14N-2具有D4h对称性和1A1g电子态,能量比14N-1高2.71 kcal/mol. 第三稳定结构14N-3可由1个Si原子戴在13N-3的Si6-Si8-Si10面上形成,能量比14N-1高25.78 kcal/mol.

图3 RuSin (n=10~14)原子簇的低能量结构
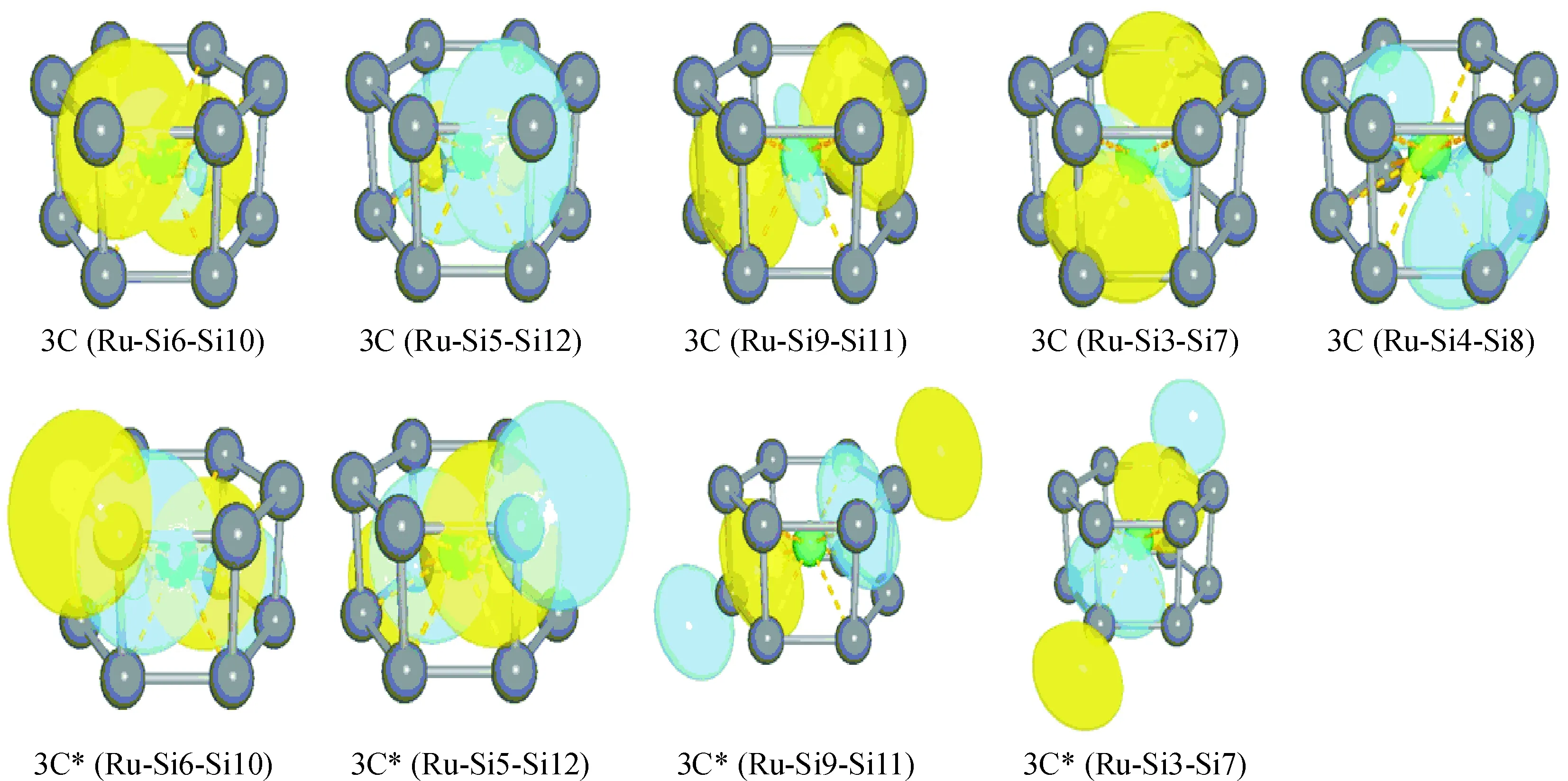
图4 自然键轨道分析(NBO)预测的RuSi12基态结构中的9个三中心键
Figure 4 Nine three-centered (3C) bonds in the most stable structure of the RuSi12cluster predicted by natural bond orbital (NBO) analysis
2.2 相对稳定性
为了讨论不同尺寸的RuSin原子簇的相对稳定性,计算其基态结构的平均结合能(Eb)和二阶差分能(Δ2E),公式如下:
Eb(RuSin)=
[E(Ru)+nE(Si)-E(RuSin)]/(n+1),
(1)
Δ2E(RuSin)=
E(RuSin-1)+E(RuSin+1)-2E(RuSin),
(2)
其中,E(M)代表了M体系的能量.
RuSin原子簇平均结合能随原子簇尺寸的变化情况如图5所示. RuSin原子簇的平均结合能随n的增大而逐渐增加,说明原子簇的稳定性是随其尺寸的增加而逐渐增强的. 当n=9 和12时,存在个峰,说明相应的原子簇比相邻的原子簇更稳定. RuSin的结合能也比相应尺寸的纯硅原子簇的结合能大,说明掺杂Ru原子有助于提高Si原子簇的稳定性.

图5 RuSin(n=2~13)原子簇基态结构的平均结合能(Eb)随原子簇尺寸的变化
Figure 5 Size dependence of the average binding energies (Eb) for the most stable isomers of the RuSin(n=2~13) clusters
二阶差分能也是一个反映原子簇相对稳定性的敏感的量. RuSin原子簇的二阶差分能也在n=9和12时有较大值(图6),说明相应的原子簇具有更高的稳定性,这与平均结合能的结果一致.

图6 RuSin(n=2~13)原子簇基态结构的二阶差分能(Δ2E)随原子簇尺寸的变化
Figure 6 Size dependence of the second-order energy differences (Δ2E) for the most stable isomers of the RuSin(n=2~13) clusters
2.3 HOMO-LUMO能隙
最高占据轨道和最低占据轨道的能量差称为HOMO-LUMO能隙,是反映原子簇化学活性的一个重要参数. 图7显示,RuSi、RuSi3、RuSi5、RuSi9、RuSi11和RuSi12具有相对较大的HOMO-LUMO能隙,表明这些原子簇具有相对较高的化学稳定性.
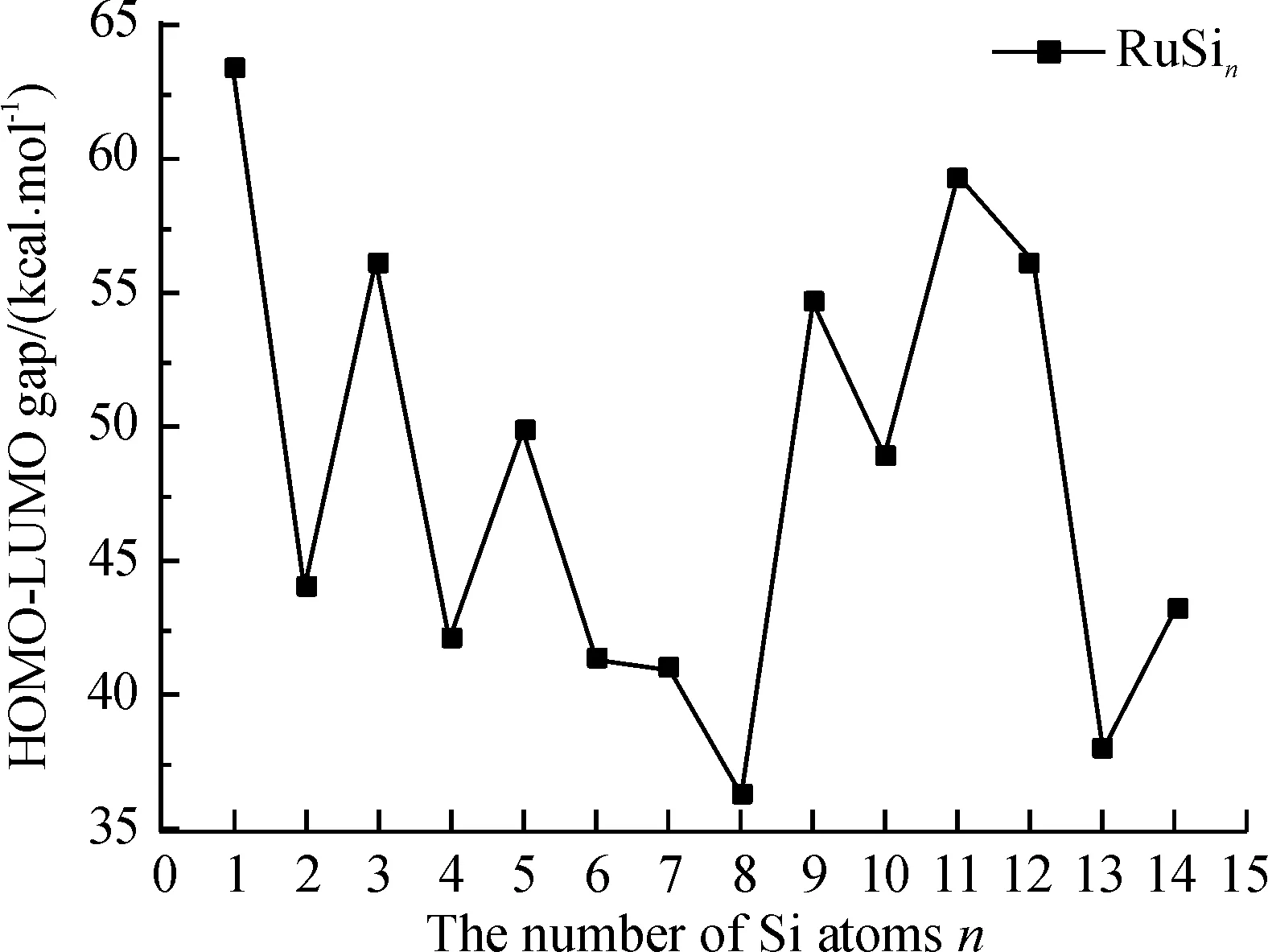
图7 RuSin(n=2~13)原子簇基态结构的HOMO-LUMO能隙随原子簇尺寸的变化
Figure 7 Size dependence of the HOMO-LUMO gaps for the most stable isomers of RuSin(n=2~13) clusters

图8 RuSin(n=1~14)原子簇基态结构的垂直电离势(VIP)和垂直电子亲合势(VEA)随原子簇尺寸的变化
Figure 8 Size dependence of the vertical ionization potentials (VIP) and vertical electron affinities (VEA) for the most stable isomers of the RuSin(n=1~14) clusters
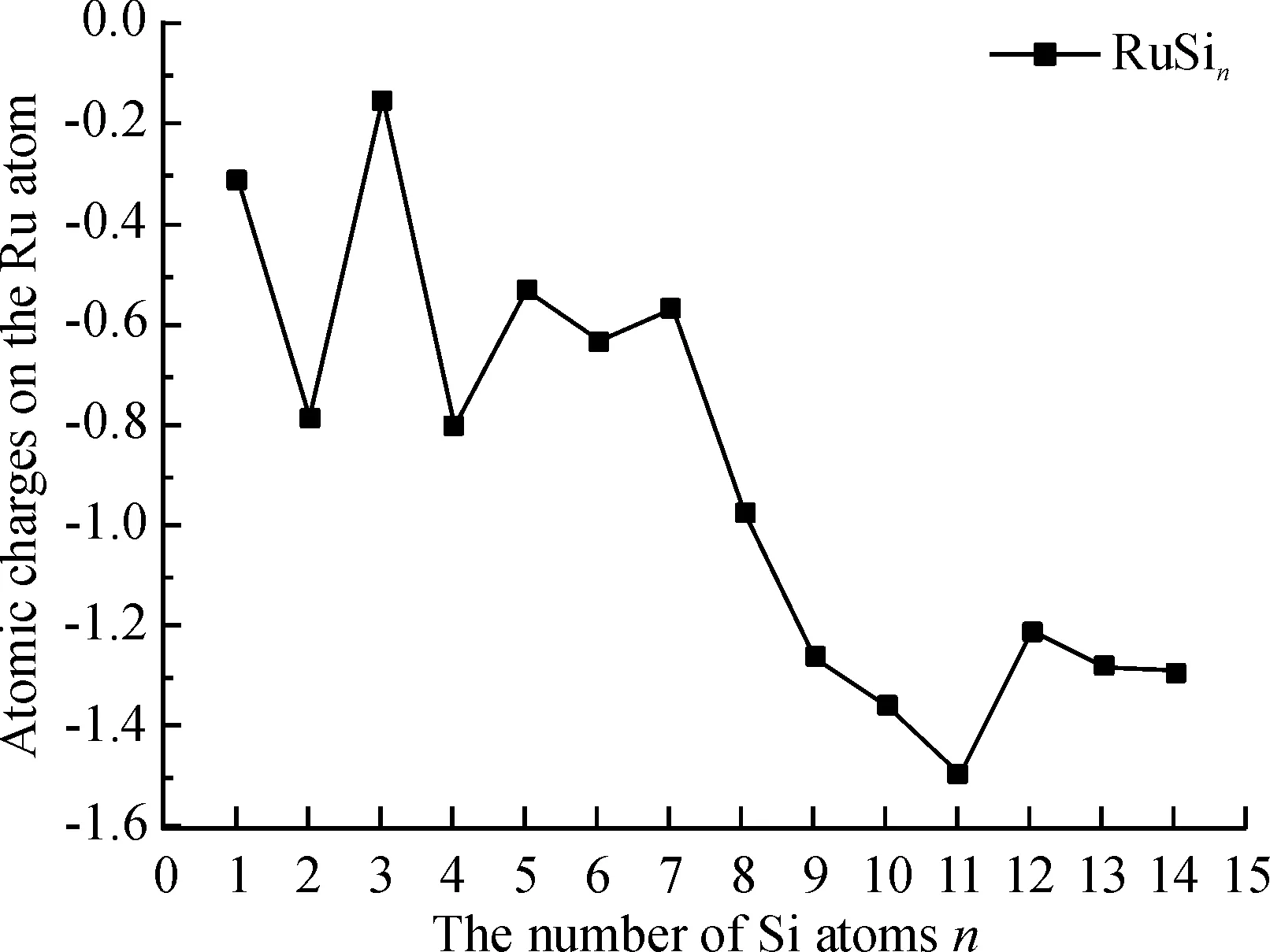
图9 RuSin(n=1~14)原子簇基态结构的电荷转移随原子簇尺寸的变化
Figure 9 Size dependence of the charge transfer from the Sinmoiety to the Ru atom for the most stable isomers of the RuSin(n=1~14) clusters
2.4 电子性质
电离势(IP)和电子亲合势(EA)也能在一定的程度上反映原子簇的稳定性. RuSin原子簇的垂直的电离势(VIP)和垂直的电子亲合势(VEA)定义如下:
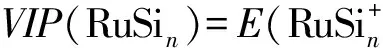
E(optimized RuSin),
(3)
VEA(RuSin)=E(optimized RuSin)-
(4)
如图8所示,RuSin原子簇的垂直电离势都在6.7 eV以上,峰值出现在n=1、3、6、11和13,表明相应的原子簇较难被电离. RuSin原子簇的电子亲合势随着硅原子数n的增大呈增加的趋势. 此外,RuSi6、RuSi8和RuSi13原子簇具有相对较大的VEA值,说明这些原子簇较容易获得一个电子变为负离子.
此外对RuSin原子簇的基态结构进行电荷转移分析(图9). RuSin中电子总是从Sin转移到Ru原子,意味着Sin扮演着电子供体的角色,因为Ru原子的d轨道需要更多电子. 从n=8起,电子转移突然增多,由于Ru原子开始被更多的Si原子包围,可以提供给Ru更多的电子.
3 结论
采用B3LYP/6-311SDD方法对RuSin(n=1~14)原子簇进行了系统的研究. 对每个原子簇,考虑了大量可能的异构体结构. 结果表明,在RuSin原子簇的基态结构中,Ru原子的位置逐渐从原子簇表面转移到原子簇内部;当n=12时,Ru原子完全陷入原子簇内部,形成1个以Ru为中心的硅笼结构. 平均结合能Eb和二阶差分能Δ2E分析表明,RuSi12具有较高的稳定性,可以作为Si纳米线的结构单元的潜在候选者. HOMO-LUMO能隙分析显示,RuSi、RuSi3、RuSi5、RuSi9、RuSi11和RuSi12比其相邻的原子簇具有更高的化学稳定性. 电荷布局分析显示,RuSin原子簇中电子总是从Sin向Ru原子转移.
参考文献:
[1] Ho K M, Shvartsburg A, Pan B C, et al. Structures of medium-sized silicon clusters[J]. Nature, 1998, 392(6676): 582-585.
[2] Hossain D, Hagelberg F, Pittman C, et al. Structures and stabilities of clusters of Si12, Si18, and Si20 containing Endohedral Charged and Neutral Atomic Species[J]. Journal of Physical Chemistry C, 2007, 111(37): 13864-13871.
[3] Ngan V T, Gruene P, Claes P, et al. Disparate effects of Cu and V on structures of exohedral transition metal-doped silicon clusters: a combined far-infrared spectroscopic and computational study[J]. Journal of the American Chemical Society, 2010, 132(44): 15589-15602.
[4] Claes P, Janssens E, Ngan V T, et al. Structural identification of caged vanadium doped silicon clusters[J]. Physical Review Letters, 2011, 107(17): 173401.
[5] Beck S M. Mixed metal-silicon clusters formed by chemical reaction in a supersonic molecular beam: Implications for reactions at the metal/silicon Interface[J]. Journal of Chemical Physics, 1989, 90(11): 6306-6312.
[6] Hiura H, Miyazaki T, Kanayama T. Formation of metal-encapsulating Si cage clusters[J]. Physical Review Letters, 2001, 86(9): 1733-1736.
[7] Hanna S N, Rao B K, Jena P. Magic numbers in metallo-inorganic clusters: chromium encapsulated in silicon cages[J]. Physical Review Letters, 2002, 89(1): 016803.
[8] Lu J, Nagase S. Structural and electronic properties of metal-encapsulated silicon clusters in a large size range[J]. Physical Review Letters, 2003, 90(11): 115506.
[9] Grubisic A, Ko Y J, Wang H P, et al. Photoelectron spectroscopy of lanthanide-silicon cluster anions LnSin- (3≤n≤13; Ln=Ho, Gd, Pr, Sm, Eu, Yb): prospect for magnetic silicon-based clusters[J]. Journal of American Chemical Society, 2009, 131(30): 10783-10790.
[10] Lenssen D, Bay H L, Mesters S, et al. Growth and structural characterization of semiconducting Ru2Si3[J]. Journal of Luminescence, 1999, 80(1-4): 461-465.
[11] Lindholm N, Morse M. Rotationally resolved spectra of jet-cooled RuSi[J]. Journal of Chemical Physics, 2007, 127(8): 084317.
[12] Gueorguiev G K, Pacheco J M. Silicon and metal nanotemplates: size and species dependence of structural and electronic properties[J]. Journal of Chemical Physics, 2003, 119(19): 10313-10317.
[13] Becke A D. Density-functional thermochemistry. III. The role of exact exchange[J]. Journal of Chemical Physics, 1993, 98(7): 5648-5652.
[14] Lee C, Yang W, Parr R G. Development of the colic-salvetti correlation-energy formula into a functional of the electron density[J]. Physical Review B, 1988, 37(2): 785-789.
[15] Xiao C Y, Abraham A, Quinn R, et al. Comparative study on the Interaction of scandium and copper atoms with small silicon clusters[J]. Journal of Physical Chemistry A, 2002, 106(46): 11380-11393.
[16] Xiao C Y, Hagelberg F, Lester W A. Geometric, energetic, and bonding properties of neutral and charged copper-doped silicon clusters[J]. Physical Review B, 2002, 66(7): 075425.
[17] Xu H G, Zhang Z G, Feng Y, et al. Vanadium-doped small silicon clusters: Photoelectron spectroscopy and density-functional calculations[J]. Chemical Physics Letters, 2010, 487(4-6): 204-208.
[18] Andrae D, Haeussermann U, Dolg M, et al. Energy-ajusted ab initio pseudopotentials for the second and third row transiton elements[J]. Theoretica Chimica Acta, 1990, 77(2): 123-141.
[19] Hay P J, Wadt W R. Ab Initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg[J]. Journal of Chemical Physics, 1985, 82(1): 270-283.
[20] Anderson T, Haugen H K, Totop H. Binding energies in atomic negative ions[J]. Journal of Physical and Chemical Reference Data, 1999, 28(6): 1511-1533.
[21] Sansonetti J E, Martin W C. Handbook of basic atomic spectroscopic data[J]. Journal of Physical and Chemical Reference Data, 2005, 34(4): 1559-2259.
[22] Huber K P, Herzberg G. Molecular Spectra and Molecular Structure, Constants of diatomic molecules (vol. IV) [M]. New York: Van Nostrand Reinhold, 1979.
[23] Wang H M, Liu Y F, Haouari H, et al. Raman spectra of ruthenium dimers[J]. Journal of Chemical Physics, 1997, 106(16): 6534-6537.
[24] Du J G, Sun X Y, Wang H Y. The confirmation of accurate combination of functional and basis set for transition-metal dimers: Fe2, Co2, Ni2, Ru2, Rh2, Pd2, Os2, Ir2, and Pt2[J]. International Journal of Quantum Chemistry, 2008, 108(9): 1505-1517.
[25] Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford CT, 2004.
[26] Qin W, Lu W C, Zhao L Z, et al. Stabilities and fragmentation energies of Sinclusters (n=2-33)[J]. Journal of Physics: Condensed Matter, 2009, 21 (45): 455501.

[28] Wu Z J, Su Z M. Electronic structures and chemical bonding in transition metal monosilicides MSi(M=3d, 4d, 5d elements)[J]. Journal of Chemical Physics, 2006, 124(18): 184306.
[29] Yang J C, Xu W G, Xiao W S. The small silicon clusters Sin(n=2-10) and their anions: structures, themochemistry, and electron affinities[J]. Journal of Molecular Structure, 2005, 719(1-3): 89-102.
[30] Guo L J, Zhao G F, Gu Y Z, et al. Density-functional investigation of metal-silicon cage clusters MSin(M=Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn;n=8-16)[J]. Physical Review B, 2008, 77(19): 195417.

