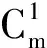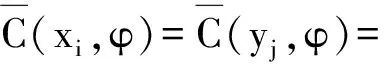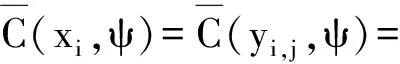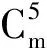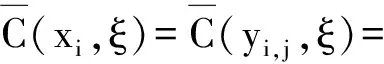复合交叉圈的邻点可区别全色数
杨 超, 姚 兵, 王宏宇
(西北师范大学数学与统计学院, 兰州 730070)
1 引言及概念
图的染色和标号是当今图论学科中十分活跃的分支,它们在编码理论、通讯网络、物流等方面均有应用[1-4].图的邻点可区别全染色的概念第一次被张忠辅等[5]提出,并提出了以下的邻点可区别全染色猜想:
猜想1[5]对于阶数不小于 2的简单连通图G,有
然而, 诸多文献的结论表明, 解决上述猜想较困难. 近些年来,对此猜想的研究成果不断报道[6-10],Wang等[7]对平面图验证了邻点可区别全染色猜想, 取得了较好的结论. 令平面图G的最小圈长为g(G), 他们证明了: 当g(G)≥6和Δ(G)=4时,当g(G)≥8和Δ(G)=3时,5. 然而,对于最小圈长g(G)≤5的平面图的邻点可区别全染色还有待研究, 没有一般的方法来确定他们的邻点可区别全色数.
本文研究一类复合交叉圈,验证了邻点可区别全染色猜想,得到了它在最小圈长不超过5时的邻点可区别全色数,从而促进了对最小圈长不超过5的平面图的邻点可区别全染色问题的研究. 文中论及的图均为有限、无向简单图, 且采用标准的图论术语和符号,可参见文献[11].

引理1[5]设Pn是n阶路. 当n≥4时,当n=2,3时,
引理2[5]设Cn是n阶圈(n≥4),则
引理3[5]如果G有相邻的 Δ-顶点, 则
定义2 一个双圈图G=G[Cm,Cn]满足:
(1)G是平面图,且包含一个m个顶点的圈Cm=x1x2…xmx1和一个n个顶点的圈Cn=y1y2…yny1;
(2)E(G)=E(Cm)∪E(Cn), 以及|V(G)|≤m+n-2;

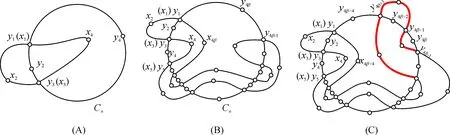
显然, 双圈图G=G[Cm,Cn]的最大度Δ(G)=4, 最小度δ(G)=2, 且没有1度和3度顶点. 相对于圈Cn,如果圈Cm的一条路P(xi,xj)=xixi+1…xj满足V(Cn)∩V(P(xi,xj))={xi,xj},称路P(xi,xj)为双圈图G的一个基于圈Cn的耳朵,简称为耳朵,Cn叫做基圈. 如果路P(xi,xj)位于基圈Cn内(外),就把路P(xi,xj)叫做内(外)耳. 注意到, 双圈图G=G[Cm,Cn]的2个圈相对于耳朵概念是对称的,为可区分,以下不把圈Cn的路叫做耳朵. 容易观察到: 双圈图G=G[Cm,Cn]至少有2个耳朵,G的圈Cm是耳朵的并,它的内耳数目等于外耳数目. 设基圈Cn的一条路Q=ysys+1…ytyt+1…ykyk+1…yl上连接了G的2个内(外)耳P(ys,yl)⊂Cm和P(yt,yk)⊂Cm. 如果在路Q的子路ys+1…yt-1,yt+1…yk-1和yk+1…yl-1上,再没有G的其他耳朵,把路P(ys,yl)和P(yt,yk)叫做G的双(外)耳,不是双耳的耳朵叫做单耳. 按耳朵分类, 可将双圈图分为3类,如图1所示.

图1 双圈图的类型
定义3 一个交叉圈是双圈图G=G[Cm,Cn],满足:(1)当|V(G)|=m+n-2时,G仅含1个单内耳和1个单外耳;(2)当|V(G)| 推广定义3如下: (1)Hk是连通平面图,且含圈Cn1,Cn2,…,Cnk和Cm;Δ(Hk)=4; 符号[s,t]表示非负整数集{s,s+1,s+2,…,t},其中s和t均为整数,且满足0≤s 图中达到最大度的顶点叫做 Δ-顶点. 证明设f为交叉圈G=G[Cm,Cn] 的一个邻点可区别全染色, 且minf(V(G)∪E(G))=令f(uv)=α.下面分 2 种情形证明. 在H中,仅需考虑对顶点w以及它的2条关联边uw和wv进行染色,使得新图H满足定义H的一个正常全染色g如下:g(uw)=a1,a1g(wv)=α;g(w)C{α,a1,g(u),g(v)};g(t)=f(t),t(S1{uv})⊆(S2{uw,w,wv}),其中S1=V(G)∪E(G),S2=V(H)∪E(H). 在H中,仅需考虑对顶点w以及它的2条关联边uw和wv进行染色,使得新图H满足(G).定义H的一个正常全染色h如下:令h(wv)=b1,b1h(w)=α;h(uw)C{α,b1,h(u),h(ux)};h(t)=f(t),t(S1{uv})⊆(S2{uw,w,wv}),其中S1=V(G)∪E(G),S2=V(H)∪E(H). 综合以上讨论,引理得证. □ 运用相似于引理4的证明方法,可证得 引理6 设交叉圈G=G[Cm,Cn]不含相邻的Δ-顶点,且每一个2度顶点都相邻2个Δ-顶点,则=5. 证明运用数学归纳法. 下面证明用5种颜色就可以对G进行邻点可区别全染色.定义交叉圈G的一个正常全染色h如下:h(x1)=h(y1)=1,h(x3)=h(y3)=2,h(y2)=h(y4)=4,h(x2)=h(x4)=3,h(y1y2)=h(y3y4)=3,h(y2y3)=1,h(y1y4)=2,h(x1x2)=h(x3x4)=4,h(x2x3)=h(x1x4)=5. 情形2.假设圈Cm与基圈Cn相交β次,则为便于区别,用表示圈表示圈Cn,不妨设见图2B.由归纳假设,G有一个邻点可区别全染色φ,使得minφ(V(G)∪E(G))=不失一般性,给出G的一个邻点可区别全染色φ如下:φ(xi)=φ(yj)=1,i,j[1,4β]且i,j≡1(mod 4);φ(xi)=φ(yj)=2,i,j[1,4β]且i,j≡3 (mod 4);φ(yj)=4,j[1,4β]e;φ(xi)=3,i[1,4β]e;φ(yjyj+1)=3,j[1,4β]o;φ(yjyj+1)=1,j[1,4β]且j≡2 (mod 4);φ(y1y4β)=φ(yjyj+1)=2,j[1,4β]且j≡0 (mod 4);φ(xixi+1)=4,i[1,4β]o;φ(xixi+1)=φ(x1x4β)=5,i[1,4β]e. 图2 引理6的相关图 综合以上讨论,引理得证. □ 定理1 如果一个交叉圈G=G[Cm,Cn]不含相邻的Δ-顶点,则 证明情形1.交叉圈G=G[Cm,Cn]不含相邻的Δ-顶点,且每一个2度顶点都相邻2个Δ-顶点,由引理6,得 综合以上讨论,定理得证. □ 引理7 设交叉k-圈Hk(k≥1)不含相邻的Δ-顶点,且每一个2度顶点都相邻2个Δ-顶点,则 证明运用数学归纳法. 由归纳假设,Hk有一个邻点可区别全染色ζ,使得minζ(V(Hk)∪E(Hk))=不失一般性,给出Hk的一个邻点可区别全染色ζ如下:ζ(yi,j)=1,i[1,k],j[1,4β]且j≡1(mod 4);ζ(yi,3)=2,i[1,k],j[1,4β]且j≡3(mod 4);ζ(yi,j)=4,i[1,k],j[1,4β]e;ζ(yi,jyi,j+1)=3,i[1,k],j[1,4β]o;ζ(yi,1yi,4β)=ζ(yi,jyi,j+1)=2,i[1,k],j[1,4β]且j≡0(mod 4);ζ(yi,jyi,j+1)=1,i[1,k],j[1,4β]且j≡2(mod 4);ζ(xi)=1,i[1,2kβ]o;ζ(xi)=2,i[2kβ,4kβ]o;ζ(xi)=3,i[1,4kβ]e;ζ(xixi+1)=4,i[1,4kβ]o;ζ(xixi+1)=ζ(x1x4kβ)=5,i[1,4kβ]e. 图3 引理7的相关图 引理得证. 定理2 如果一个交叉k-圈Hk(k≥2)不含相邻的Δ-顶点,则 证明情形1.如果交叉k-圈Hk不含相邻的Δ-顶点,且每一个2度顶点都相邻2个Δ-顶点,则由引理7, □ 参考文献: [1] 周向前, 姚兵, 程辉.关于0-可旋转树[J]. 华南师范大学学报:自然科学版, 2011(4): 54-57. Zhou X Q,Yao B,Cheng H. On 0-rotatable trees[J].Journal of South China Normal University:Natural Science Edition,2011(4): 54-57. [2] 吴康, 薛展充. 关于圈图Cn的连2距k着色计数[J]. 华南师范大学学报:自然科学版, 2007(2): 7-10. Wu K,Xue Z C.The counting of double distancedk-coloring in cycle[J].Journal of South China Normal University:Natural Science Edition,2007(2): 7-10. [3] 卜月华, 朱俊蕾. 不含4-圈和7-圈的平面图的列表均匀染色[J]. 湖南师范大学自然科学学报,2007, 30(4): 6-10. Bu Y H,Zhu J L.Equitable list coloring of planar graphs without 4- and 7- cycles[J].Journal of Natural Science of Hunan Normal University,2007, 30(4): 6-10. [4] 魏白, 黄元秋, 郭婷,等. 一类图在小亏格曲面上的嵌入[J]. 湖南师范大学自然科学学报,2012, 35(5): 24-29. Wei B,Huang Y Q,Guo T,et al.Embedding on surfaces with small genus of one type of graph[J].Journal of Natural Science of Hunan Normal University,2012, 35(5): 24-29. [5] 张忠辅, 陈祥恩, 李敬文, 等.关于图的邻点可区别全染色[J]. 中国科学:A 辑, 2004, 34(5): 574-583. [6] 姚兵,程辉,姚明,等.图着色下的树顶点邻集的行为[J].数学物理学报,2011, 31(2): 567-576. Yao B, Cheng H, Yao M, et al. Behaviors of vertex neighbors of trees under graph colorings[J]. Acta Mathematica Scientia, 2011, 31(2): 567-576. [7] Wang W F,Wang Y Q. Adjacent vertex distinguishing total coloring of graphs with lower average degree[J]. Taiwanese Journal of Mathematics, 2008, 12(4): 979-990. [8] Wang Y Q,Wang W F. Adjacent vertex distinguishing total colorings of outerplanar graphs[J]. Journal of Combinatorial Optimization,2010,19(2):123-133. [9] Hulgan J. Concise proofs for adjacent vetex-distinguishing total colorings[J]. Discrete Mathematics, 2009,309(8): 2548-2550. [10] Wang H Y. On the adjacent vertex-distinguishing total chromatic numbers of the graphs with Δ(G)=3[J]. Journal of Combinatorial Optimization, 2007,14(1): 87-109. [11] Bondy J A,Murty U S R. Graph theory with applications[M]. London, Basingstoke, New York:The MaCmillan Press ltd, 1976.


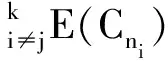
2 主要结果及其证明