多约束在线高斯伪谱末制导方法
杨 良,郑宗贵,徐 衡,陈万春,周 浩
(1.北京航空航天大学 宇航学院,北京 100191;2.第二炮兵装备研究院,北京 100085;3.北京空天技术研究所,北京 100074)
高超声速飞行器在低层稠密大气中的飞行环境特别恶劣,因此,需要设计满足多约束要求的末段制导方法。要实现对终端落点和落角的控制,对动力学方程进行线化后的制导律能很好地满足要求[1-3]。然而对于终端速度,由于其非线性较强,无法线性化,控制相当困难。对此,赵汉元提出了调节攻角的速度控制制导律[4],但该制导律需要飞行器进行快速滚转运动,对于多类飞行器而言并不适用。
近年来,数值方法和计算机技术的发展大大提高了求解非线性最优控制问题的速度。伪谱法[5-6]就是其中一种。Ross I通过勒让德伪谱法提出了一种基于时钟序列保持的伪谱反馈制导策略,并进行了卫星控制和再入制导的在线反馈研究[7-8]。崔锋通过勒让德伪谱法也进行了再入制导的在线反馈研究[9]。伪谱反馈为终端多约束问题尤其是终端速度控制提供了一种很好的求解方法。
本文进行了在线高斯伪谱的反馈方法研究,建立了高斯伪谱法的初值猜测策略,并应用于高超声速飞行器的末段飞行,成功实现了对落角、落速的控制,在无反馈信息的最后一个制导周期引入比例导引方法[10]保证落点精度。蒙特卡罗打靶实验表明,该制导方法能够很好地满足多项终端约束条件,并且具有很高的鲁棒性。高斯伪谱法的微分矩阵满秩,因此其计算结果相比勒让德伪谱具有更高的精度[11]。
1 方法介绍
1.1 方法概述
本文采用高斯伪谱法对非线性状态方程进行末端轨迹优化;在一个制导周期内,采用时钟保持机制将最优控制指令代入实际飞行过程;在同一制导周期上,利用上一周期的全弹道信息及当前状态量进行制导指令的在线重构;在下一制导周期上,重复上述步骤,并在最后一个制导周期应用比例导引方法击中目标,如图1所示。

图1 方法流程图
1.2 高斯伪谱反馈与指令保持
高斯伪谱反馈是通过高斯伪谱法求解基本的最优控制问题,获得离散的时变反馈控制指令。反馈的目的是消除由模型不确定性、外部干扰以及估计误差造成的影响。指令的保持是根据上一步求得的以时间为自变量的控制指令,采用图2的形式进行保持。
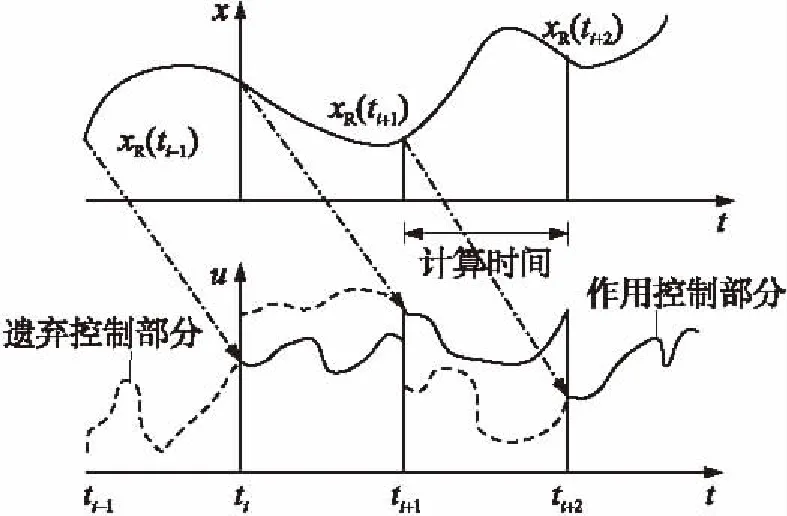
图2 指令保持示意图[7]
图2中,xR(ti)为当前时刻的状态量,u为控制量,ti和ti+1分别为当前时刻和下一个制导时刻。文献[5]指出成功运用反馈控制的关键是能够快速地得到一条开环控制,高斯伪谱法对光滑问题具有的指数收敛特性可以保证这种快速性。
1.3 初值估计策略
对于非线性规划问题,为了加快寻优算法的速度,可以充分利用上一制导周期的最优结果:
(1)
式中:t0是初始时刻;tf是终端时刻,τi∈[-1,1]是高斯拉格朗日(LG)节点;ti,tj∈[t0,tf],是LG节点在时域内的分布;Li(t)为Lagrange插值多项式;X(ti)为上一制导周期优化的LG节点上的状态量和控制量。
对于当前制导周期,去除上一制导周期所用时间tc,可以得到新的时间节点:
进而可以使用上一制导周期的优化结果来估计当前制导周期的初值:
通过后面的仿真结果可以看出,将X(tj)作为初值代入非线性规划问题求解器进行计算具有较高的计算效率。
2 飞行器动力学模型
2.1 动力学方程
考虑大气相对于地球相对静止的无动力三自由度质点弹道运动学方程[12]:
式中:x,y,z为位置坐标;v为速度;m为飞行器质量;γ为弹道倾角;φ为航向角;α为攻角;ε为侧倾角;g=μ/r2是重力加速度,r为地心距,μ为地球重力加速度常数;u1,u2为控制量;升力FL和阻力FD为
式中:q=ρv2/2为动压,CL为升力系数,CD为阻力系数,Sref为飞行器参考面积;ρ为大气密度,其表达式为
ρ=ρ0e-βH
(6)
式中:ρ0为海平面大气密度,H为高度,β为密度常数。
2.2 约束条件
从结构和热防护的角度出发,要求高超声速飞行器在飞行过程中满足动压和过载约束:
式中:qmax和nz,max根据具体飞行器来选取。
考虑到高超声速飞行器在末段飞行过程中的恶劣环境,除了要求攻角α和倾侧角ε应该保持在一定的范围之内,其变化率也必须保持在一定的范围之内,即
2.3 优化性能指标
为使优化得到的攻角和倾侧角足够光滑,选取各控制量的平方和最小作为性能指标。同时,为了增加寻优算法的收敛区域,增强制导算法的鲁棒性,把末端状态量的约束加入到性能指标中,具体形式为
式中:K为加权系数。
对于某些特殊的擦边界最优控制问题,由于原问题在擦边界的过程中不再是光滑的最优控制问题,伪谱法不再具有指数收敛特性,即失去解算的快速性。这时通过改变性能指标可以将该问题转化为光滑问题,进而获得指数收敛特性,可以进行在线优化。
3 仿真结果及分析
3.1 飞行器模型
本文采用的飞行器模型为美国在“猎鹰”计划支持下发展的新一代高超声速远程快速精确打击武器系统——通用航空飞行器(CAV)。该飞行器具有乘波体构型,依靠气动力在大气层内滑行,具有升阻比大、飞行马赫数高、飞行空间环境恶劣、对控制系统要求较高等特点。NASA公布的CAV的总体参数如表1所示。

表1 飞行器总体参数
CAV在低层稠密大气的气动系数公式为
其中各气动参数可参考文献[13]。
3.2 任务要求
飞行器的任务要求是在初始拉偏和过程拉偏的情况下满足以下终端约束条件:
攻角、侧倾角以及控制量的变化范围为

任务要求的主要难点在于速度控制,飞行器的速度对升力、阻力非常敏感,也是长周期的控制过程,调节能力非常有限,因此要求制导律在末段飞行段进行精确的控制。
3.3 不同初始条件下的制导结果
考虑飞行器不同初始条件下的无干扰弹道,可以验证高斯伪谱反馈制导方法对不同初始条件的适应性。表2列出了5种初始条件,初速均为1 718 m/s。表3为终端状态约束。

表2 初始条件

表3 终端状态约束
图3为空间弹道曲线,可以看出不同初始条件下的弹道均能满足终端状态约束,并且以相似形式击中目标。
图4和图5分别为不同初始条件下的速度曲线和弹道倾角曲线。由于终端状态相同,不同初始条件的弹道在末段飞行后期差异不大,因此对于弹道的调整主要集中在末段飞行的前期。虽然末段飞行前期的速度和弹道倾角差异较大,但都能满足终端马赫数为3和终端弹道倾角为-80°的约束条件。

图3 空间弹道
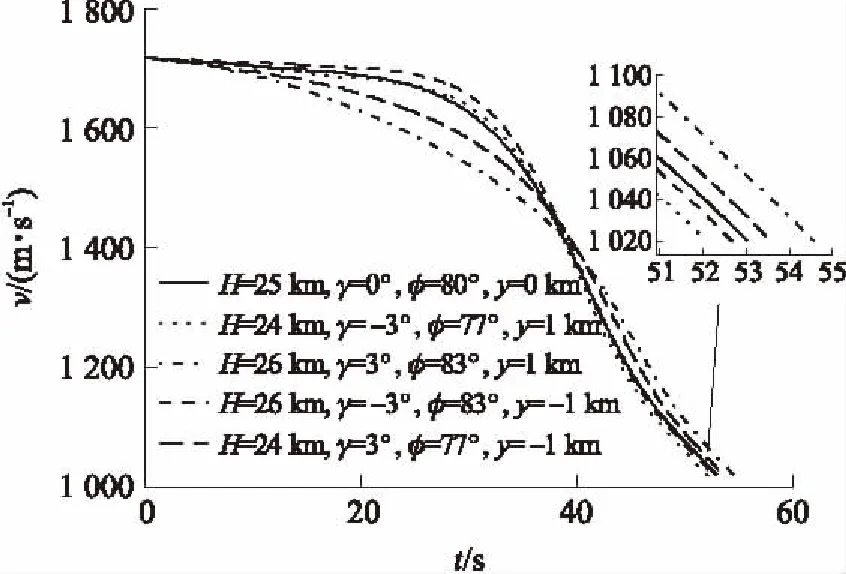
图4 速度曲线

图5 弹道倾角曲线
图6为不同初始条件下的攻角变化曲线。攻角在末段飞行后期差异不大,在末段飞行前期差异很大,弹道的调节也主要是集中在末段飞行的前期。不同初始条件下的终端攻角都能达到0°的约束条件。
图7为每一制导周期内高斯伪谱法单次优化的计算时间。5种初始条件情况均在主频3.3 GHz计算机上使用Matlab 7.0进行仿真,计算时间tcal均集中在0.1 s左右。由于不存在过程干扰,优化时间主要用于克服LG节点之间的龙格现象。结果表明,选取0.8 s的制导周期可以满足指令解算的需要,同时相比50 s以上的末段飞行时间也可以保证合理的制导精度。

图6 攻角曲线

图7 计算时间
表4为不同初始条件下的终端状态偏差。5种初始条件下的脱靶量M和速度偏差都能保证在百分之一的数量级,终端弹道倾角和攻角偏差能保证在万分之一的数量级。

表4 终端状态偏差
3.4 扰动模型
建立风速、大气密度和温度随高度变化的拉偏模型:
式中:v(H),ρ(H),T(H)分别为风速、大气密度和温度干扰随高度变化的函数,v(H)最大能达到50 m/s,ρ(H)最大能达到0.09ρst,T(H)最大能达到30 K。Δv,Δρ,ΔT为[-200%,200%]的拉偏系数。
飞行器的气动拉偏模型是在标准气动升阻力系数的基础上加上偏差值:
考虑扰动模型后,飞行器速度控制的难度增加,需要在末段飞行段之前的巡航段对飞行器进行关机控制。假设飞行器在巡航段匀速飞行,可以利用高斯伪谱法寻找最优关机时刻,并作为初值代入末段飞行段中。
3.5 过程扰动下的蒙特卡洛打靶结果
为了测试高斯伪谱反馈制导方法的鲁棒性,在带关机控制的情况下进行1 000次蒙特卡罗打靶实验,其中考虑初始状态拉偏项和3.4中所述拉偏项,如表5所示,表中,μ为均值,3σ为均方差。由于速度对升力、阻力较为敏感,且速度控制能力有限,因此升力、阻力拉偏相对较小。

表5 蒙特卡洛打靶拉偏分布
图8和图9为终端位置在x和y方向上的误差PΔx,PΔy概率分布,各个方向的误差都在0.1 m以内。图10和图11为终端速度和终端弹道倾角的误差概率PΔv,PΔγ分布,终端速度和终端弹道倾角大部分分布在约束范围之内。图12为终端攻角的误差概率PΔα分布,终端攻角主要集中在-0.7°附近,满足约束条件。

图8 终端位置x方向误差概率分布

图9 终端位置y方向误差概率分布
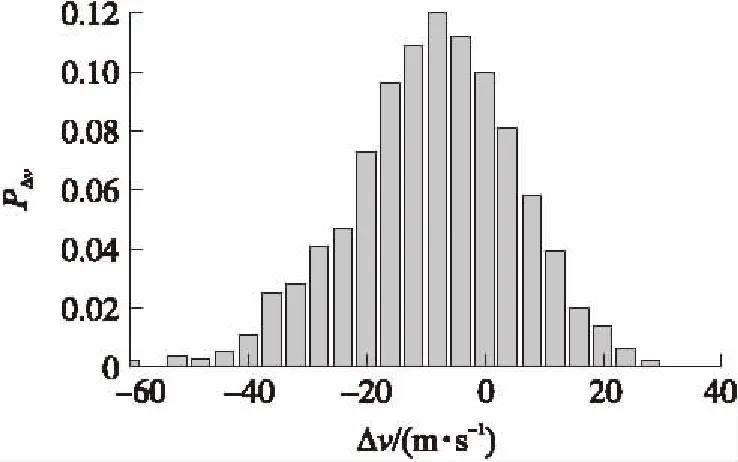
图10 终端速度误差概率分布

图11 终端弹道倾角误差概率分布

图12 终端攻角误差概率分布
对终端状态偏差进行统计,脱靶量的期望为0.092 m,落入概率为100%;速度误差的期望为-6.913 m/s,落入概率为81.2%;弹道倾角偏差的期望为0.040 40°,落入概率为93.3%;攻角偏差的期望为-0.611°,落入概率为99.7%。因此,飞行器终端脱靶量、速度偏差、弹道倾角偏差以及攻角偏差的期望都很小,满足约束条件。值得注意的是,攻角、弹道倾角和速度需要进行全程能量管理才能保证,这反映出在线高斯伪谱制导的效果。落入概率为终端状态偏差落入约束范围内的概率。终端速度偏差的落入概率最低,说明终端速度最难控制。蒙特卡罗打靶结果表明,高斯伪谱反馈制导方法在恶劣的飞行环境下具有很好的制导能力和鲁棒性。
4 结束语
本文针对高超声速飞行器,基于高斯伪谱法,建立了一种在末段飞行段满足多种约束条件的在线反馈制导方法。使用上一制导周期优化结果作为初值猜测的策略,在解算过程中可以有效地加速算法收敛。在最后一个制导周期加入比例导引方法可以保证终端命中点具有较高的精度。不同初始条件下的制导结果说明,该方法具有很好的适用性。各种拉偏情况下的蒙特卡洛打靶实验表明,该方法在恶劣的飞行环境下具有较好的稳定性和鲁棒性,能有效地对终端速度进行控制。
[1] KIM M,GRIDER K V.Terminal guidance for impact attitude angel constrained flight trajecories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,10(6):852-859.
[2] LEE Yong-in,RYOO C K,KIM E.Optimal guidance with constraints on impact angle and terminal acceleration[R].AIAA 2003-5795,2003.
[3] LU P,DOMAN D B,SCHIERMAN J D.Adaptive terminal guidance for hypervelocity impact in specified direction[J].Journal of Guidance,Control,and Dynamics,2006,29(2):269-278.
[4] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997.
ZHAO Han-yuan.Entry dynamics and guidance[M].Changsha:National University of Defence Technology Press,1997.(in Chinese)
[5] DAVID A B,GEOFFREY T H.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1 435-1 440.
[6] FAHROO F,ROSS I M.Costate estimation by a Legendre pseudospectral method[R].AIAA-98-4 222,1998.
[7] ROSS I M,SEKHAVAT P.Optimal feedback control:foundations,examples,and experimental results for a new approach[J].Journal of Guidance,Control,and Dynamics,2008,31(2):307-321.
[8] BOLLONO K P,ROSS I M.A pseudospectral feedback method for real-time optimal guidance of reentry vehicles[C]//Proceedings of the 2007 American Control Conference.New York City,USA:The American Antomatic Control Council,2007:11-13.
[9] 崔锋.采用伪谱法的再入飞行器最优反馈制导方法[J].中国制造业信息化,2011,40(19):42-45.
CUI Feng.The optimal feedback guidance control method of entry vehicles based on pseudospectral method[J].Manufacture Information Engineering of China,2011,40(19):42-45.(in Chinese)
[10] PAUL Z.Tactical and strategic missile guidance[M].Cambridge,Massachusetts:Charles Stark Draper Laboratory,Inc.,1997.
[11] GARG D,PATTERSON M A,HAGER W W,et al.A unified framework for the numerical solution of optimal control problems using pseudospectral methods[J].Automatica,2010,46(11):1 843-1 851.
[12] VINH N X.Flight mechanics of high-performance aircraft[M].Cambridge,England,U.K:Cambridge Univ Press,1993.
[13] TERRY H P.A common aero vehicle model,description,and employment guidance[R].Arlington:Schafer Corporation for AFRL and AFSPC,2003.

