从2013年高考选择(填空)题读高考命题意图

●陈尧明 (上虞区教体局教研室 浙江绍兴 312300)

2013年高考早已尘埃落定，盘点和研究这些高考试题，无不折射出命题者的智慧和他们的匠心独具.这些试题既蕴含着诸多的数学思想、方法及数学的本质，同时又传递和引领着今后一段时期的数学教育理念和教学的改革方向.本文以2013年浙江省数学高考理科选择(填空)题为基本题，分析其命题意图.

1 紧密联系课本内容

选择题第 1，2，3，4，5，11，12 题都是课本“影子题”，即每个题目都可在课本中找到类似题，其难度相当于课本练习题或简单习题.只要基础知识扎实，前3 个题目可“一望即知”，而第 4，5，6，13，14题都在平时的练习、检测或课本的每章复习题中出现过类似的题目.只要认真复习教材，读完题目基本上就能确定解决方案.

2 重视数学本质的考查

2013年选择(填空)题不少试题都呈现出对数学本质的考查.

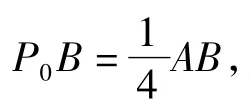
A.∠ABC=90° B.∠BAC=90°

C.AB=AC D.AC=BC

(2013年浙江省数学高考理科试题)

分析解决本题的方法颇多，可以用投影法、坐标法或基向量法，也可采用淘汰法，虽然淘汰法是求解单一选择题的有力利器，特别是当所选题目有较高难度时，更能体现出它的独到之处，但淘汰法需要对每一个选项进行验证而耗时，很不经济.

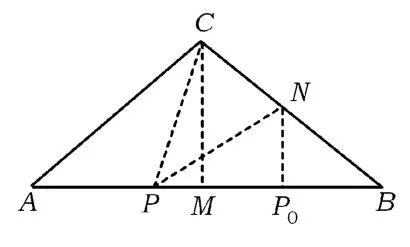
图1

学生最直接的思考方法是建立坐标系，利用坐标将几何问题转化为代数问题，进而借助函数的恒成立问题演绎出三角形的形状，这是一种单线型的思路.在思维难度高一层的是利用投影概念或基向量法，这2种方法都是基于对投影和基向量这2个数学概念上的本质理解.

如果将问题转化为极化恒等式如(a+b)2+(a-b)2=2a2+2b2，也就是我们平时常说的平行四边形的性质：平行四边形对角线的平方和等于4条边的平方和，则问题会简洁很多.

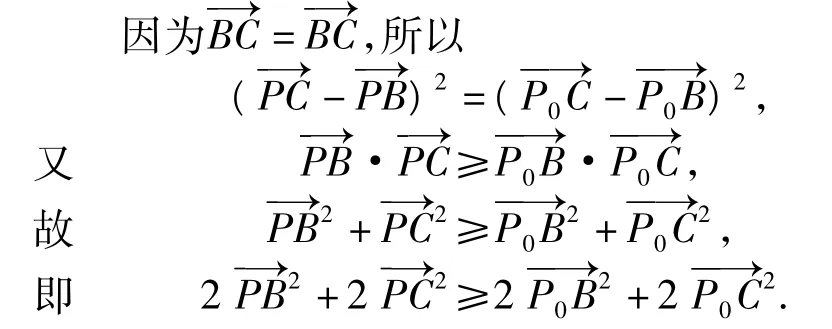
取BC中点 N，AB中点 M，联结 PC，PN，MC，P0B(如图1)，由极化恒等式可知

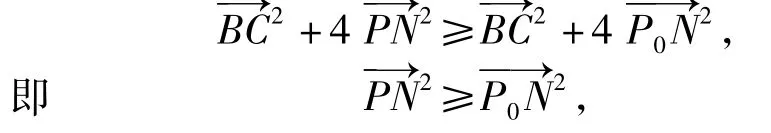
由点 P的任意性知，P0N⊥AB，即CM⊥AB，从而AC=BC.故选 D.

对创新意识的考查是对高层次理性思维的考查，要创设新颖的问题情境，构造有一定深度和广度的数学问题，注重问题的多样性，体现思维的发散性.可以说，利用极化恒等式是解决此题思维的再高层次，因为极化恒等式它剔除了问题的“浮土层”，突出了问题的数学本质，这显然也是本题的立意所在.

例2 已知 e为自然对数的底数，设函数f(x)=(ex-1)(x-1)k(k=1，2)，则 ( )

A.当k=1时，f(x)在x=1处取到极小值

B.当k=1时，f(x)在x=1处取到极大值

C.当k=2时，f(x)在x=1处取到极小值

D.当k=2时，f(x)在x=1处取到极大值

(2013年浙江省数学高考理科试题)

分析本题考查导数公式、导数的四则运算法则和极值的判定方法.我们知道，当k=1时，函数f(x)图像“穿过”点(1，0)，对应方程 f(x)=0来说，存在一个解x=1;当k=2时，函数f(x)的图像“相切”x轴于点(1，0)，对应方程f(x)=0来说，存在2个相同的解x1=x2=1.尽管图像都经过点(1，0)，但蕴藏的数学“风景”不同，具有本质上的差异.因此，基于导数本质上的理解，选项A，B肯定是错误的，考察函数f(x)=(ex-1)(x-1)2，当x＞1且趋于 +∞时，f(x)也趋于 +∞，不难知道f(x)在x=1处取到极小值.故选C.

“少考一点算，多考一点想”，从数学的本质立意，是2013年数学试题命题的一个亮点.

3 传统与创新相结合

作为高等院校的招生考试，毋容置疑应优先考虑选拔性的要求，但也应顾及一般性的要求.如何框定两者的平衡点，试题传统与创新是很好的技术点.为了控制整个选择(填空)题组的难度，试题的设置就要兼顾传统与创新这2个方面.如果试题偏重于传统题，则选拔性差;反之，如果创新题太多，不易发挥正常水平.2013年选择(填空)题的17个试题中，传统与创新比例恰当，除了第 7，8，10，16，17题外，其余均为传统题.这也成功实现了基本题的命题功能.下面以第16题为例作一诠释：

例3 在△ABC中，∠C=90°，M是BC的中点.若sin∠BAM=，则 sin∠BAC= ______.

(2013年浙江省数学高考理科试题)

分析2013年数学高考首次将解斜三角形设置在填空题中，但作为三角大题的“接班”题，既不能像大题那样“厚重”，又不失具有一定的区分度，设置一个动态的三角是情理之中，恰到好处.

不妨设 AC=1，BC=2x(见图2)，则

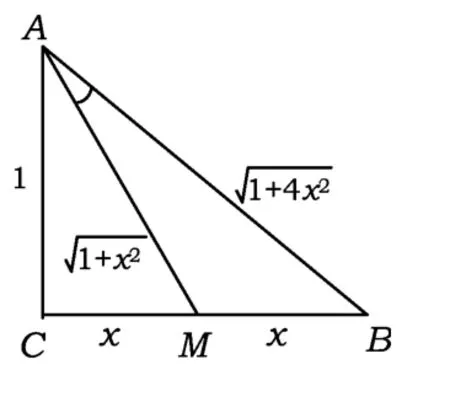
图2

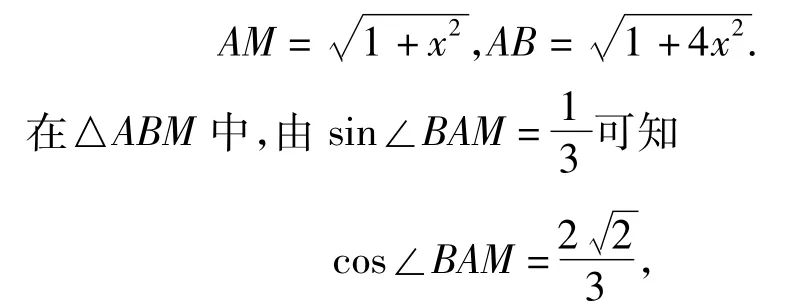
由余弦定理得

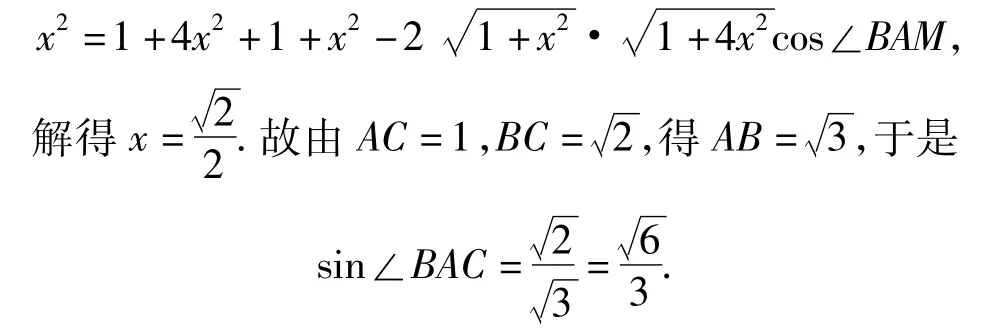
4 突出了数学能力的考查

记忆能力和观察能力是数学能力的先导，对概念、公式、性质、定理的记忆是必备的，可以说每个题目都蕴含着对记忆力和观察力的考查.第13题是典型的三视图，通过观察学生实现三维空间图形在大脑上的定格，明确该空间图形是怎样的几何体，才能准确无误地计算出几何体的体积.

空间想象能力、抽象概括能力、推理论证能力、运算求解能力是《考试说明》中已明确的四大基本能力.2013年的选择(填空)题组的设计，充分考虑了四大基本能力的考查，有些试题还同时考查了几种能力.如重点突出推理论证能力的有第7，8，10，17题，考查运算求解能力的有第 6，9，11，13，15题，考查空间想象能力的有第12题，而第7，14，16，17题又综合考查了运用数学知识和方法分析问题和解决问题的能力.

例4 将6个字母 A，B，C，D，E，F排成一排，且A，B均在 C的同侧，则不同的排法数共有______种(用数字作答).

(2013年浙江省数学高考理科试题)

分析此题考查了除空间想象能力之外的其他三大能力.按字母C的位置分类讨论：

5 加强了速度的考查功能

对数学基础知识的考查，既要全面又要突出重点，对于支撑学科知识体系的重点内容，要占较大的比例，构成数学试卷的主体.显而易见，高考试题的设计离不开试题对教材知识的覆盖面，选择(填空)题共17题，分值达78分，因而对解题速度提出了较高的要求.考生在解题时必须牢记解题的相关知识与方法，具备灵活、敏捷的解题思维，不仅要会解、解对，同时也要解得快.不同的解法，表现出解题速度的巨大差异.比如例4还可以这样解：6个字母 A，B，C，D，E，F 全排有种排法，而对于字母A，B，C 来说，“A，B 均在 C 的同侧”占了 A，B，C全排列的，因此不同的排法数共有=480种.

又如例3，也可利用中点分三角形等面积，即由 S△ABM=S△ACM得

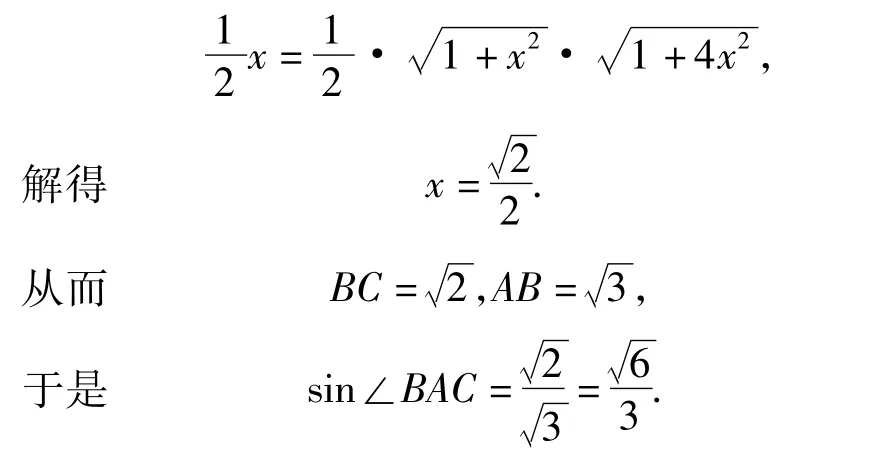
例5 设 e1，e2为单位向量，非零向量 b=xe1+ye2，x，y∈R.若 e1，e2的夹角为，则的最大值等于______.

(2013年浙江省数学高考理科试题)

分析 此题解法很多，一般用向量的代数法.根据题意，得

从上述过程不难看出，分子、分母同除以x的代数变形，对考生来说技术要求有点高，而且还应考虑到等号取到的条件是否具备.事后从学生的反馈看，学生在基本题的解答中，此题的耗时还是不少的.

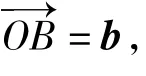
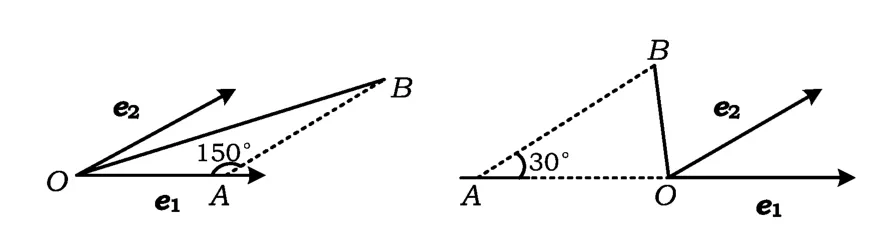
图3 图4

［1］ 中华人民共和国教育部制订.普通高中数学课程标准(实验)［M］.北京：人民教育出版社，2003.

［2］ 浙江省教育考试院.浙江省普通高考考试说明［M］.杭州：浙江摄影出版社，2013.