旋成体环形射流表面优化设计与减阻机理分析

赵刚，李芳，臧东阳

(哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001)

横流中的射流具有广泛的工程应用，如气膜的冷却［1］、污染物的驱散［2］、飞行器姿态的控制［3］等。射流在减阻领域的研究相对较少，主要集中在高超声速飞行器减阻领域。文献［4］在风洞中对高超声速钝头体模型进行了逆向喷流实验研究，并通过改变喷口压力得到了30%～45%的减阻率。文献［5］对2种喷压比下不同射流模式产生的机理进行了分析，并重点分析了湍流机制对流场的影响。周超英等［6］对超声速球头体逆向喷流流场进行数值模拟，结果显示:随着喷流总压的变化，流场可出现2种流动模态，即长射流穿透模态和短射流穿透模态。Shah等［7］对不同来流马赫数下反向喷流的减阻特性进行研究，发现阻力的降低与射流的质量流率相关。

受鲨鱼鳃裂射流的启发，赵刚等对射流平面的减阻特性进行了仿真［8-10］和转化实验研究［11］，取得了显著的减阻效果。然而，平面侧向射流与来流的相互干扰特性与旋成体上的侧向射流不同，因此，本文采用数值模拟方法研究在旋成体上开环形射流孔时的射流参数对减阻效果的影响。

1 旋成体环形射流表面设计

研究发现，在射流孔周长小于旋成体的周长时，在射流孔两侧会形成局部的高应力区，不利于减阻，因此，本文设计的射流孔为环形射流孔，旋成体仿生射流表面模型如图1所示。模型由前端的半球体和后端的圆柱体2部分组成，半球体的半径r=1 mm，圆柱体的直径d=2 mm，模型全长L=10 mm，射流孔中心距旋成体底部的距离为L1，射流孔宽度为b。

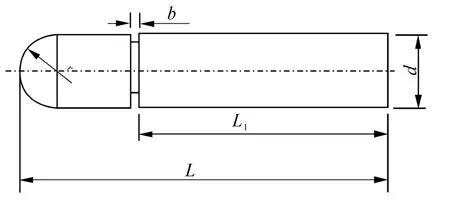
图1 环形射流旋成体模型Fig.1 Model of annular jet flow surface

2 数值模拟

2.1 控制方程和湍流模型

基本方程为

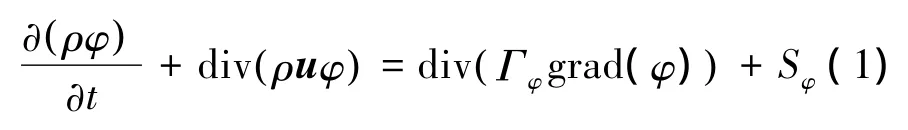
式中:ρ为流体密度，t为时间，u为速度矢量;φ为通用因变量，Sφ为广义源项，Γφ为广义扩散系数。表1给出了式(1)与连续方程、动量方程以及能量方程的对应关系，表中ui为x、y、z方向的速度分量，μ为动力粘度。

表1 控制方程中各符号的具体形式Table 1 Concrete terms of symbols in the governing equation

湍流模型选用SSTk-ω模型。与其他模型相比，SSTk-ω模型在预测近壁区绕流和旋流方面有优势。SSTk-ω流动方程如:

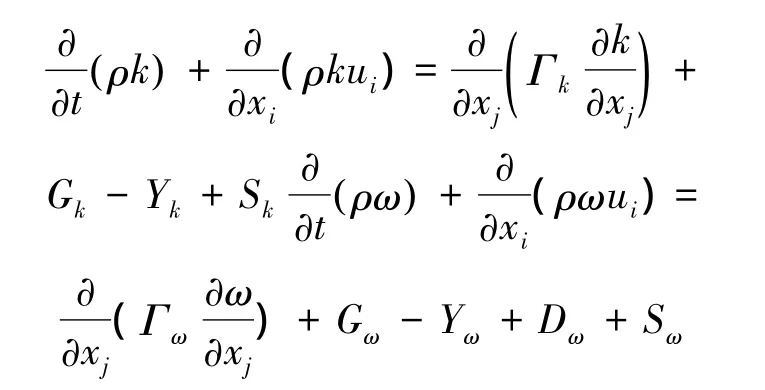
式中:Gk表示湍流的动能，Gω为 ω 方程，Γk、Γω分别代表k及ω方程的有效扩散项，Yk、Yω分别代表k及ω的发散项，Sk与Sω用户自定义，Dω代表正交发散项。

2.2 网格划分

利用ICEM CFD对计算域进行O型网格剖分，为保证计算精度，在旋成体壁面附近进行网格加密处理，所有模型除在射流孔区域网格划分不同外，其余部分采用相同的网格划分，近壁面第一层网格到壁面的距离根据下式［12］

利用

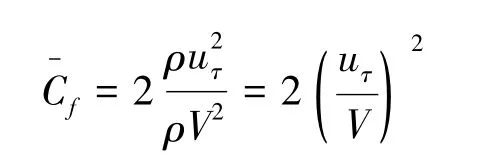
消掉uτ，得

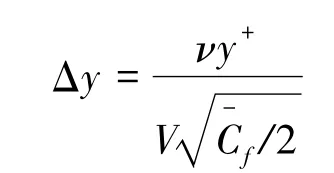
式中:y+为第一层网格到壁面的无量纲距离，uτ为壁面摩擦速度，平均摩擦阻力系数Cf如下

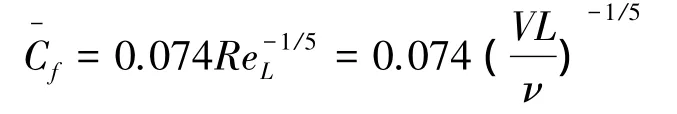
式中:L为旋成体长度，ν为运动粘度系数。

旋成体边界层厚度δ计算式为

通过网格无关性验证，选取全局最大网格尺寸参数为5 mm;采用增强型壁面函数，壁面第一层网格尺寸参数为 0.002 mm，y+为 2～4，网格增长率为1.1，并使法线方向上有15个节点以上，以满足SSTk-ω模型对y+的要求。计算域为10d×10L(计算域入口距旋成体球面顶点的距离为2L)，网格节点总数为 91×104，单元总数为 89×104，旋成体表面网格划分情况如图2所示。

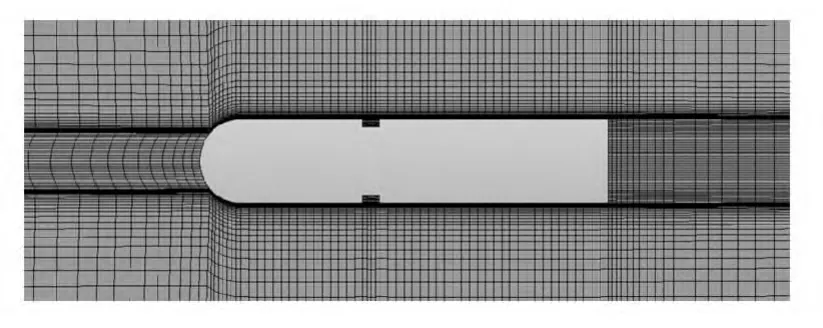
图2 旋成体表面网格Fig.2 Surface mesh of body of revolution

2.3 边界条件

计算域入口:速度入口边界，湍流强度为5%，湍流直径为20 mm，出口为压力出口;旋成体壁面及射流孔内壁为无滑移绝热壁面;射流孔入口为速度入口，湍流强度为5%;远场边界为对称边界;方程残差为1×10-4;选用基于压力基求解器，离散格式为二阶迎风离散格式。

3 减阻性能研究及减阻机理分析

旋成体仿生环形射流表面减阻效果用减阻率表示，计算式为

式中:FS为光滑旋成体模型的总阻力，FJ为射流表面旋成体模型的总阻力，η为总阻力减阻率。

模型表面所受总阻力F包括压差阻力f'和粘性阻力f，即F=f'+f，其中

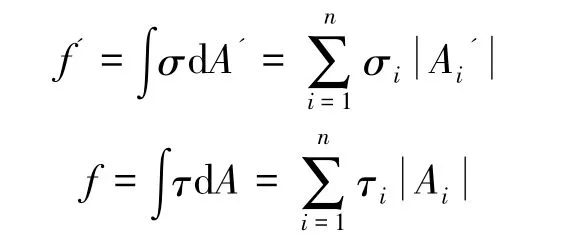
式中:σ为旋成体壁面压应力;σi为旋成体壁面离散单元压应力;A'为旋成体壁面沿主流场方向面积投影;Ai＇为旋成体壁面离散单元沿主流场方向投影;τ为旋成体壁面剪应力;τi为旋成体壁面离散单元剪应力;A为旋成体壁面面积;Ai为旋成体壁面离散单元面积。

压差阻力减阻率计算式为

式中:fs＇为光滑旋成体模型的压差阻力，fj＇为射流表面旋成体模型的压差阻力，m为压差阻力减阻率。

粘性阻力减阻率计算式为

式中:fs为光滑旋成体的粘性阻力，fj为射流旋成体模型的粘性阻力，n为粘性阻力减阻率。

射流改变了边界层内的流场结构，减小了旋成体壁面的摩擦阻力并节约了能量。将单位时间内因摩擦阻力减小所节约的能量和射流供给所需能量的比值定义为节能效率K，K值越大，节能效果越好，计算式如下

式中:AJ为射流孔面积。

3.1 正交设计

采用数值模拟与正交试验相结合的方法，分析旋成体射流表面减阻因素及减阻机理。影响旋成体环形射流模型减阻节能效果的参数主要包括主流场速度、射流速度、射流孔宽度及射流孔位置4个因素，为增大设计结果的通用性，分别对射流孔宽度和射流孔位置参数进行量纲一化，为了较全面的了解每个因素对减阻效果的影响程度，每个因素取3个水平，选用L9(34)正交表。

试验因素选择:A为主流场速度、B为射流速度、C为射流孔宽度b与旋成体直径d的比值、D为射流孔距旋成体底部的距离L1与旋成体长度L的比值，试验方案选择及结果见表2～6。

表2 试验方案及结果分析Table 2 Experiment scheme and results analysis

表3 各因素对压差阻力减阻率影响正交试验结果极差分析Table 3 Range analysis of orthogonal experiment results for various factors on the efficiency of pressure drag reduction %

表4 各因素对粘性阻力减阻率影响正交试验结果极差分析Table 4 Range analysis of orthogonal experiment results for various factors on the efficiency of viscous drag reduction %

表5 各因素对总阻力减阻率影响的正交试验结果极差分析Table 5 Range analysis of orthogonal experiment results for various factors on the efficiency of total resistance of drag reduction %

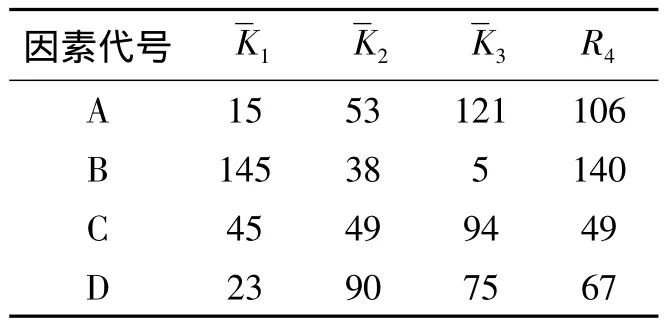
表6 各因素对节能效率影响的正交试验结果极差分析Table 6 Range analysis of orthogonal experiment results for various factors on the Energy-efficiency

3.2 模拟结果与分析

图3为各因素不同水平均值对压差阻力、粘性阻力、总阻力减阻率以及节能效率的影响规律，由极差分析可知:

1)分析射流参数对总阻力的影响规律可知，射流孔位置对总阻力的影响最大，当其余因素固定不变时，射流孔位置与总阻力减阻率呈线性关系，射流孔离旋成体的底部越远，减阻效果越好;射流速度对总阻力的影响其次，射流速度与总阻力减阻率呈抛物线关系，当射流速度为4 m/s时，减阻效果最好;射流孔宽度与总阻力减阻率呈抛物线关系，当b=0.2d时，减阻效果最好;主流场速度的变化对总阻力的影响最小，主流场速度与总阻力减阻率呈抛物线关系，当主流场速度为20 m/s时，减阻效果最好。

2)各射流参数对压差阻力的影响规律与总阻力一致。

3)分析射流速度对粘性阻力的影响可知，射流速度对粘性阻力影响最大，当其余因素固定不变时，射流速度与粘性阻力减阻率呈线性关系，随着射流速度的增大，粘性阻力减阻率增大;主流速度对粘性阻力的影响其次，主流场速度与粘性阻力减阻率呈线性关系，随着主流场速度的增大，粘性阻力减阻率减小;射流孔宽度与粘性阻力减阻率呈抛物线关系，当射流孔宽度为0.2d时，粘性阻力减阻率最大;射流孔位置对粘性阻力的影响最小，二者呈抛物线关系，当射流孔距旋成体底部的距离为0.6L时，粘性阻力减阻率最大。

4)分析射流参数对节能效率的影响规律可知，射流速度对节能效率影响最大，当其他因素固定不变时，射流速度与节能效率呈线性关系，射流速度越大，节能效率越小;主流场速度对节能效率影响其次，主流场速度与节能效率呈线性关系，随着主流场速度的增大，节能效率增大;射流孔位置与节能效率呈抛物线关系，当射流孔位置居中时，节能效果最好;射流孔宽度对节能效率影响最小，射流孔宽度与节能效率呈线性关系，随着射流孔宽度的增大，节能率逐渐增大。

由极差分析可知，节能效率的最优组合为7号模型，即当主流场速度为30 m/s、射流速度为2 m/s、射流孔宽度为0.3d、射流孔位于旋成体中部时节能效果最好，最大节能效率为262，介于“壁面吹吸”和“智能蒙皮”［13］的节能效率之间(“壁面吹吸”和“智能蒙皮”的节能效率分别为150和300)。

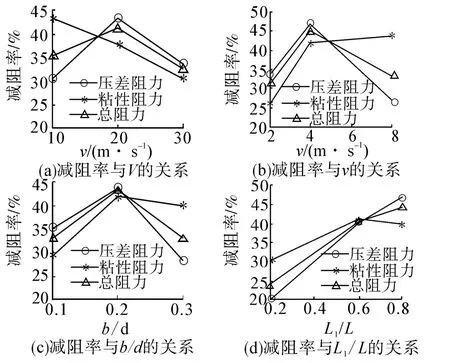
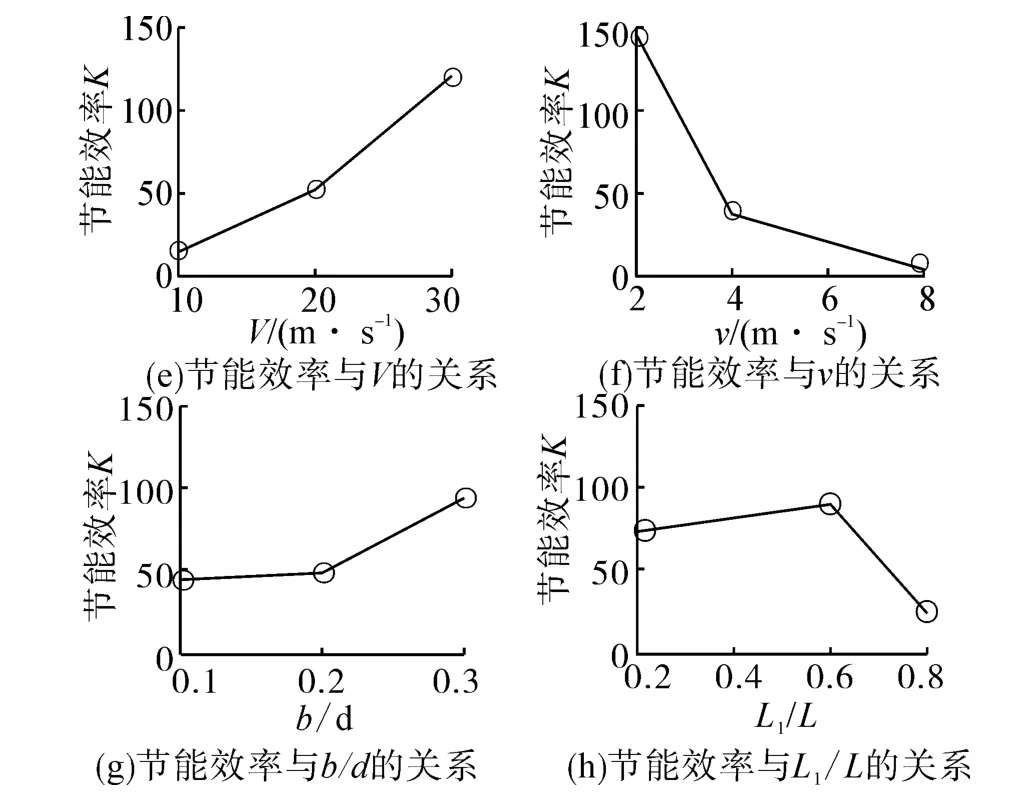
图3 各因素水平对减阻率和节能效率的影响结果Fig.3 Results for various factors on the efficiency of drag reduction and saving efficiency

从构成总阻力的各阻力单元看，本文所建立的模型压差阻力占总阻力的比重为62%，粘性阻力占总阻力的38%，所以对各影响因素来说，压差阻力减阻率几乎与总阻力减阻率有相同的变化规律。

3.3 减阻机理分析

3.3.1 环形射流旋成体减小粘性阻力的原因

图4是光滑旋成体在主流场速度为10 m/s时与2号实验模型旋成体壁面剪应力对比云图。

图4 旋成体壁面剪应力云图Fig.4 Stress nephogram for wall of body of revolution

分析图4可知，在射流孔迎流面和背流面旋成体壁面剪应力明显降低，其原因可以通过图5中的距离壁面同一高度处的速度对比得到解释。图5为光滑旋成体和环形射流旋成体相同位置的速度对比云图，图5(c)中δ+为监测点至壁面的距离与边界层厚度δ的比，δ+取值相同时，除了在射流孔附近，其余部分环形射流壁面的速度均小于光滑旋成体壁面的速度。由此可推出环形射流旋成体壁面附近流场的速度梯度减小，边界层粘性底层的厚度增加，因此粘性阻力减小。

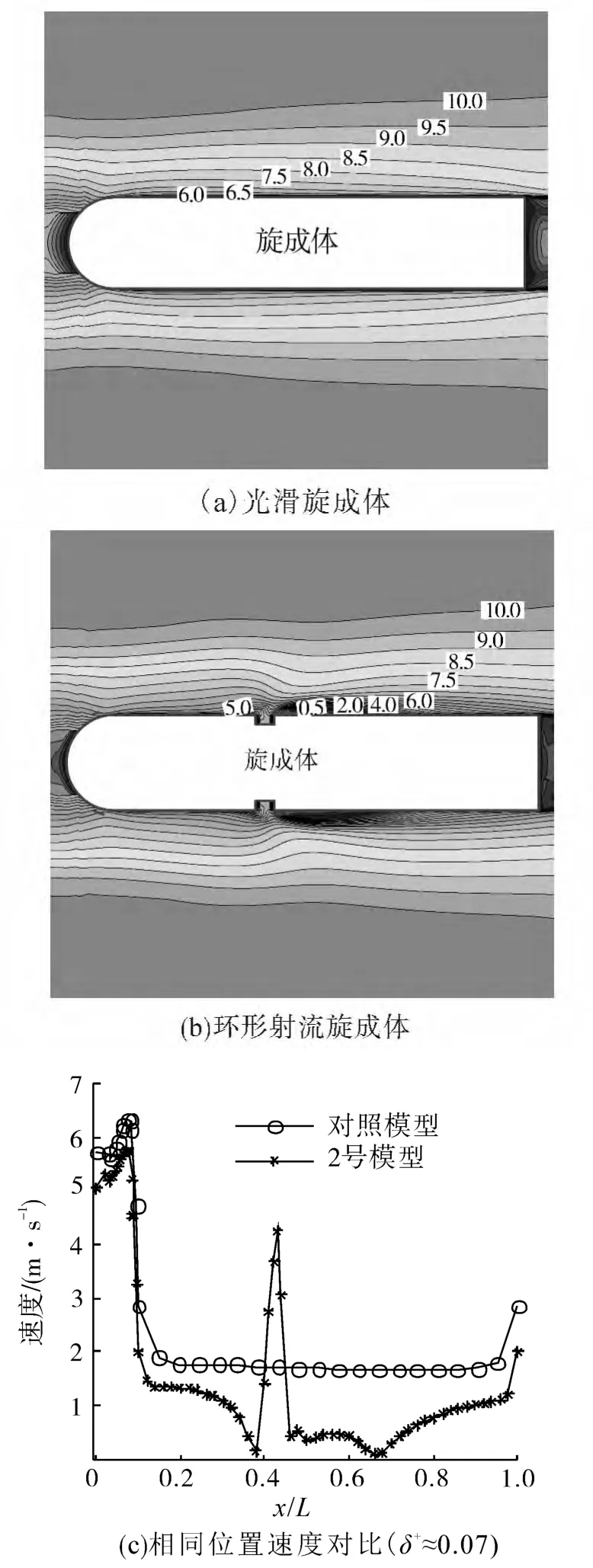
图5 环形射流旋成体与光滑旋成体近壁区速度对比Fig.5 Comparison of near-wall velocities between the annular jet flow and the smooth bodies of revolution

分析图5可知，在射流孔迎流面和射流孔下游存在低速区，其主要原因是射流对来流的阻挡，分别在射流孔迎流面和背流面形成局部高压区和局部低压区，在逆压梯度的作用下形成逆流区，在逆流区内边界层底层速度方向与主流场方向相反，近壁面处形成的剪应力作为一种附加动力作用于环形射流旋成体壁面，达到了减小粘性阻力的目的。

3.3.2 环形射流旋成体表面对压差阻力的影响

在本文的数值模拟条件下，旋成体的压差阻力主要来自于底部阻力。底部阻力系数的计算公式为

式中:Sb为旋成体底部面积;SM为旋成体最大横截面积;pb＜p∞，可通过增大旋成体底部压力来减小旋成体的底部阻力。图6给出了2号实验模型和光滑旋成体在主流场速度为10 m/s时底压曲线及云图。

图6 环形射流旋成体与光滑旋成体底部静压对比Fig.6 Comparison of static pressure between the annular jet flow and the smooth bodies of revolution

分析图6可知，环形射流旋成体的底部压力大于光滑旋成体的底部压力，表明环形射流表面在一定程度上减小了旋成体前后的压力差。

图7为2号模型与光滑旋成体底部尾流区速度曲线对比。分析图7可知，2号模型旋成体底部回流区长度(旋成体底部中心位置到后尾迹平均流向速度为零的点之间的距离)大于光滑旋成体回流区长度值，其原因是:射流速度远低于主流速度，射流的穿透能力较弱，射流基本被封锁在边界层内，边界层内的低速流体不断向下游延伸，能够对旋成体底部流体进行补充，继而推迟边界层的分离点以增加回流区的范围。较长的回流区长度表明环形射流旋成体尾迹的低压中心远离旋成体的后表面，从而使旋成体前后表面的压差减小。

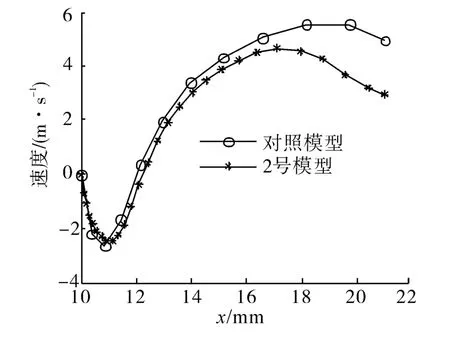
图7 尾流区速度曲线Fig.7 Velocity curves in zone of wake

综上，环形射流旋成体通过增大逆流区的范围和边界层的厚度来减小粘性阻力，通过增大底部静压和回流区长度来减小压差阻力，继而实现减阻目的。

4 结论

1)环形射流旋成体具有明显减阻、节能效果，7号模型节能效果最好，最大节能效率为262，介于“壁面吹吸”和“智能蒙皮”之间，此时的减阻率为27.74%，表明射流减阻具有较好的工程应用前景。

2)环形射流旋成体各射流参数均具有节能效果，各射流参数对节能效率影响显著性依次为:射流速度、主流场速度、射流孔位置、射流孔宽度。射流孔位置与节能效率呈抛物线关系，射流速度、主流场速度、射流孔宽度与节能效率呈线性关系，随着主流场速度、射流孔宽度增大，节能效率增大，随着射流速度增大，节能效率减小。

3)射流对主流场的阻碍作用，在射流孔迎流面和背流面形成逆流区，逆流区近壁面形成的剪应力作为一种附加动力能够显著减小粘性摩擦阻力;由于射流的推力作用，使得射流孔下游边界层厚度增大，速度梯度减小，进一步减小了粘性摩擦阻力;由于射流流体对旋成体底部流体的补充，使得边界层的分离点推迟，压差阻力减小。

［1］YU Y.Effect of hole configurations on film cooling from cylindrical inclined holes for the application to gas turbine blades［D］.Baton Rouge:Louisiana State University，2007:1-3.

［2］姜国强，任秀文，李炜.横流环境湍射流涡动力学特性数值模拟［J］.水科学进展，2010，21(3):307-314.JIANG Guoqiang，REN Xiuwen，LI Wei.Numerical simulation of vorticity dynamics for turbulent jet in crossflow［J］.Advances in Water Science，2010，21(3):307-314.

［3］蔡晋生，刘秋洪.超声速流场中侧向射流的数值研究［J］.空气动力学学报，2010，28(5):553-558.CAI Jinsheng，LIU Qiuhong.Numerical investigation of lateral jets in supersonic cross-flows［J］.Acta Aerodynamica Sinica，2010，28(5):553-558.

［4］VENUKUMAR B，JAGADEESH G，REDDY K P J.Counterflow drag reduction by supersonic jet for a blunt body in hypersonic flow ［J］.Physics of Fluids，2006，18(11):81041-81044.

［5］CHEN Liwei，WANG Guolei，LU Xiyun.Numerical investigation of a jet from a blunt body opposing a supersonic flow［J］.Journal of Fluid Mechanics，2011，684:85-110.

［6］周超英，纪文英，张兴伟，等.超声速钝体逆向喷流减阻的数值模拟研究［J］.应用力学学报，2012，29(2):159-164.ZHOU Chaoying，JI Wenying，ZHANG Xingwei，et al.Numerical investigation on counter-flow jet drag reduction of a bluff body in supersonic flow ［J］.Chinese Journal of Applied Mechanics，2012，29(2):159-164.

［7］SHAH S B H，LU X Y.Computational study of drag reduction at various freestream flows using a counterflow jet from a hemispherical cylinder［J］.Engin Appl Comput Fluid Mech，2010，4(1):150-163.

［8］ZHAO Gang，GU Yuqing，ZHENG Jinxing，et al.A testing platform based on bionics drag reduction theory for friction resistance［J］.Communications in Information Science and Management Engineering，2012，2(5):34-39.

［9］ZHAO Gang，ZHAO Hualin，SHU Haisheng，et al.Simulation study of bionic jetting direction influence on drag reduction effect［J］.Advances in Nature Science，2010，3(2):17-26.

［10］谷云庆，赵刚，赵华琳，等.仿鲨鱼鳃部射流减阻特性的仿真研究［J］.兵工学报，2012，33(10):1230-1236.GU Yunqing，ZHAO Gang，ZHAO Hualin，et al.Simulation study on drag reduction characteristics of bionic jet flow based on shark gill［J］.Acta Armamentarii，2012，33(10):1230-1236.

［11］赵刚，谷云庆，许国玉，等.仿生射流表面减阻特性实验研究［J］.中南大学学报:自然科学版，2012，43(8):3007-3012.ZHAO Gang，GU Yunqing，XU Guoyu，et al.Experimental study on drag reduction characteristics of bionic jet surface［J］.Journal of Central South University:Science and Technology，2012，43(8):3007-3012.

［12］张成春，任露泉，王晶，等.旋成体仿生凹坑表面流场控制减阻仿真分析［J］.兵工学报，2009，30(8):1066-1072.ZHANG Chengchun，REN Luquan，WANG Jing，et al.Simulation on flow control for drag reduction of revolution body using bionic dimpled surface ［J］.Acta Armamentarii，2009，30(8):1066-1072.

［13］葛铭纬.基于近壁相干结构的湍流减阻主动控制研究［D］.北京:清华大学，2011:1.GE Mingwei.Study on active control of turbulence for drag reduction based on near-wall coherent structures［D］.Beijing:Tsinghua University，2011:1.