随机搜索变量方法在滞后回归模型中的应用

曾丽娟

(中山大学新华学院，广东 广州 510642)

大量的医学研究[1]表明，大气污染对人体呼吸系统会造成较大的损害，空气污染物的增加在一定程度上使得呼吸系统疾病的患病率上升.因此，研究空气污染与呼吸疾病患病的关系，具有重要的意义.

目前，不少的研究工作者对空气污染物与呼吸疾病的关系进行了分析[2-3].李宁等[3]采用时间序列方法建立呼吸系统疾病日门诊量的自回归模型，并分别将污染物SO2, NO2,PM10和PM2.5加入到模型中，得到对应4种污染物的回归方程.然而，这种方法侧重于对病人数的单一建模，而且忽略了空气污染物的滞后效应，具有一定的局限性.相比之下，时间序列滞后回归模型同时考虑了自变量在当前时刻以及滞后时刻对因变量的影响，用该模型来分析空气污染物与呼吸疾病患病人数的关系，更能体现空气污染物对人体呼吸系统损害的滞后效应.

因此，本文将建立空气污染物与患呼吸疾病人数的时间序列滞后回归模型，并运用随机搜索变量选择方法(Stochastic Search Variable Selection,SSVS)[4-5]进行空气污染变量及滞后变量的选择.SSVS的基本思想是通过建立一个层次贝叶斯正态混合模型，利用Gibbs抽样[6]从后验分布中抽样，借助示性变量来判别变量是否被选入模型，最终得到后验概率最高的子模型.相比于传统的变量选择准则，如AIC准则，SSVS避免了计算所有可能子模型的模型信息，具有潜在的优越性.

1 滞后回归模型的统计结构

(1)

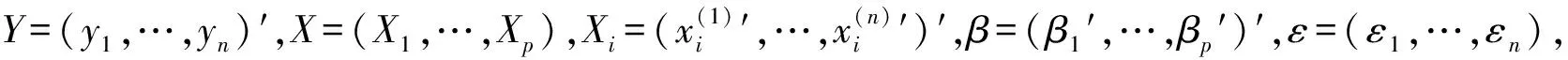
2 滞后回归模型的贝叶斯推断

为了将SSVS运用于滞后回归模型的自变量选择，引入示性变量γ=(γ1′,…,γp′)′,γi=(γi,0,γi,1,…,γi,d)′,i=1,…,p.示性变量γi,j的作用是：当所选择模型包含xi,j项时，则γi,j=1，反之，则γi,j=0.在下面的推断中，根据自变量顺序和滞后阶数大小对示性变量进行重新排序，γ=((γ1,γ2,…,γd+1),…,(γ(p-1)(d+1)+1,…,γp(d+1))),其中,γj,j=1,2,…,p(d+1)取值为0或1.下面为模型参数设定相应的先验信息：

1)系数β的每个分量看成来自由不同方差的两个正态分布组成的混合正态分布：

(2)

3)对于正态分布，当均值已知方差未知时，σ的共轭先验分布为逆Gamma分布族，即σ2|γ～IG(vγ/2,vγλγ/2),为了简化计算，超参数vγ和λγ一般选取υγ=υ和λγ=λ.

根据模型的似然函数和参数的先验分布，可以得到参数β,σ2和γ的条件后验密度：

π(β|Y,σ2,γ)∝f(Y|β,σ2)π(β|γ)∝

π(σ2|Y,β,γ)∝f(Y|β,σ2)π(σ2|γ)∝

π(γj|β,σ2,γ(-j),Y)∝f(Y|β,σ2)π(β|γ(-j),γj)π(σ2|γ(-j),γj)π(γ(-j),γj)，令

aj=f(Y|β,σ2)π(β|γ(-j),γj=1)π(σ2|γ(-j),γj=1)π(γ(-j),γj=1)，

bj=f(Y|β,σ2)π(β|γ(-j),γj=0)π(σ2|γ(-j),γj=0)π(γ(-j),γj=0)，

3 滞后回归模型的Gibbs抽样

SSVS利用Gibbs抽样从γ的后验分布中产生样本{γl,l=1,2,…,L}，并筛选出MCMC估计中γj接近1的项，作为模型选择的变量.具体抽样步骤如下：

1)设定初始状态，给出起始点φ(0)=(β(0),(σ2)(0),γ(0))；

上述过程完成了第一轮抽样，第二轮以φ(1)=(β(1),(σ2)(1),γ(1))作为初始值，重复上述过程.在足够次数的迭代后，样本序列收敛到一个独立于初始值的平稳分布.对于得到的长度为k的Gibbs序列ψ(k)=(φ(1),φ(2),…,φ(k)),舍弃前m次的预迭代，则马尔科夫链的实现值为ψ(m+1,…,k)=(φ(m+1),φ(m+2),…,φ(k))，取其平均值作为参数的估计值.

4 香港空气污染与呼吸疾病数据分析

4.1 数据的选取

4.2 贝叶斯计算

根据香港空气污染与呼吸道疾病相关文献[7],SO2,TSP,NO,NO2是造成患呼吸疾病的主要因素，故xi,t-j,i=1,…,4,j=0,1,2，对应的γ先验选取为p(γ=1)=U(0.75,0.95),其余的γ先验选取为p(γ=1)=0.5.τj取模型系数β最小二乘估计的标准差的均值，(σ2)0取方差的最小二乘估计值，超参数cj=10,j=1,…,21.R取单位阵I.SSVS选择模型变量的Gibbs抽样过程分成两个步骤，在每个步骤的抽样中均造两条马尔可夫链，燃烧期为10 000次，抽样总次数为20 000次.

2)在变量缩减模型下进行随机变量搜索，对1)中第一阶段随机搜索筛选后的自变量进行重新排序：x1,t-2,x2,t-0,x2,t-1,x2,t-2,x3,t-0,x4,t-0,x4,t-2,x7,t-0,对应的γ编号为γ1,…,γ8.超参数τj≈0.03,j=1,2,…,8,(σ2)0≈190,σ2|γ～IG(2,95).表1给出了几种模型变量选择结果,可见，具有最大后验概率的滞后回归模型包含的自变量有x7,t-0,x4,t-2,x2,t-0,x4,t-0，即湿度、NO2及其二阶滞后值、TSP对呼吸疾病影响显著.

表1 几种具有较大后验概率的模型变量选择结果

此外，示性变量的抽样结果中,γ8,γ7,γ2,γ6,γ3,γ4,γ1,γ5分别为1,0.885 2,0.691 6,0.615,0.502 7,0.482,0.405 4,0.389 1，同样说明湿度、NO2及其二阶滞后值、TSP对呼吸疾病的影响较为显著.

可见，SSVS根据γ值可以一次性准确地找出模型，表2给出了最优模型的贝叶斯估计结果.

表2 最优滞后回归模型参数的MCMC估计结果

图1和图2为对呼吸疾病人数影响最显著的污染物NO2和TSP的后验密度估计.

图1 二氧化氮后验密度

图2 悬浮粒子后验密度

因此，相关空气污染与患呼吸疾病人数的滞后回归模型表示为：

yt=0.072 74x2,t-0+0.063 55x4,t-0+0.116 9x4,t-2+0.508 6x7,t-0.

(3)

模型表明，湿度是影响患呼吸疾病人数最显著的因素，NO2的二阶滞后值对呼吸疾病的影响比当前值显著，TSP也会影响呼吸疾病患病人数.各种污染物对呼吸疾病的影响呈现正相关性，即污染物的增加均会在一定程度上使得患呼吸疾病人数上升.模型的变量选择结果中，SO2并没被筛选到模型中，这是因为在香港空气污染物中，SO2的浓度在污染水平下[7]，模型体现了香港空气污染的真实情况.

表3 两个模型的估计精度对比

5 结 论

本文将随机搜索变量选择方法运用于空气污染与呼吸疾病的时间序列滞后回归模型的变量选择中,借助WinBUGS软件，构造基于Gibbs抽样的数值计算,对模型参数进行估计.SSVS较好地结合各种空气污染物以及呼吸疾病人数的数据特征进行变量选择，得出湿度对香港患呼吸疾病人数影响最显著，NO2和TSP也是两种影响比较显著的空气污染影响因素，此外，NO2的二阶滞后值也对呼吸疾病人数有一定影响.

[1] Zanobetti A, Schwartz J. The effect of fine and coarse particulate air pollution on mortality: a national analysis[J]. Environmental Health Perspectives,2009,117(6):898-903.

[2] 刘迎春，龚洁，杨念念，等．武汉市大气污染与居民呼吸系统疾病死亡关系的病例交叉研究[J]．环境与健康杂志，2012，29(3)：241-244．

[3] 李宁，彭晓武，张本延，等．大气污染与呼吸系统疾病日门诊量的时间序列分析[J]．环境与健康杂志，2009，26(12)：1077-1080．

[4] Chen M H,Shao Q M,Ibrahim J G.Monte carlo methods in bayesian computation[M].New York:Springer,2000:267-304

[5] Kwon D, Landi M T, Vannucci M,etal. An efficient stochastic search for bayesian variable selection with High-Dimensional correlated predictors[J]. Computational Statistics & Data Analysis,2011,55(10):2807-2818.

[6] George E I,McCulloch R E. Variable selection via gibbs sampling[J]. Journal of American Statistical Association,1993,88(423):881-889.

[7] Brajer V, Mead R W, Xiao F.Valuing the health impacts of airpollution in Hong Kong[J]. Journal of Asian Economics,2006,17(1):85-102.