多重网格求解动力方程方法研究
杨 强,党亚民,赵文娇,2,杜 彬,2
(1.中国测绘科学研究院,北京 100830;2.山东科技大学,山东 青岛 266590)
多重网格求解动力方程方法研究
杨 强1,党亚民1,赵文娇1,2,杜 彬1,2
(1.中国测绘科学研究院,北京 100830;2.山东科技大学,山东 青岛 266590)
在求解动力方程过程中,引入多重网格方法,通过多次迭代、逐渐细分网格的方法简化有限元模型的计算,并进行实例分析。研究结果表明,多重网格方法运用灵活、减少运算量、计算简便且具有降噪的优势,这种方法的引入,为地壳运动和形变的研究提供了一个有用的工具。
多重网格;有限元;动力方程;迭代方法
利用大地测量技术研究地表形变特征,并进一步确定地壳的应变特征是大地测量和地球动力学主要研究内容之一。而地壳运动作为一个动态演化过程,其位移、应力随时间不断演化发展。地壳应力、应变场的动态演化过程,体现了地壳内部各物理因素的变化与影响程度[1-2]。
一个动态系统的动力特性主要包括:几何结构、边界条件和材料性质,其解析表达式则是将其质量、刚度和阻尼分布分别利用质量矩阵、刚度矩阵和粘滞矩阵表示出来,以此来确定系统运动的动力特性。解算方法很多,比较典型的方法是有限元方法[3]。
传统有限元方法的离散化过程和数值求解过程是相互独立、互无作用的,其离散化过程不能预测合适的解,往往造成计算上的浪费。而将网格划分很细,又使得代数方程组阶数过大,而精度没有提高。为了克服这种缺陷,本文将多重网格理论与有限元方法相结合,提出一种有效求解地壳动力方程的方法。
1 多重网格求解过程
多重网格方法的主要特点就是在粗网格层上迭代求解其误差方程直到误差收敛的基础上,通过插值的方法将误差校正结果返回到细网格层上进行校正。通过这种迭代、校正的过程,减少了计算量、提高了解算精度,在一定程度上弥补了传统有限元方法的不足[4-5]。
动力响应分析是一个多自由度系统问题,其动力方程可以表示为
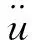
(1)
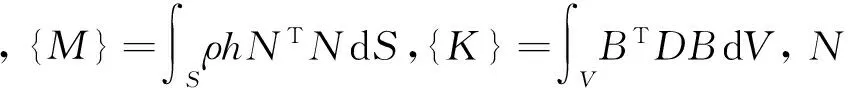
1.1 初始网格位移解算
利用有限元方法,首先求解初始网格各节点位移uk-1。初始网格划分数量较少,称为粗网格。
1.2 定义向下延拓双线性插值算子
通过双线性插值算子,获取k层网格下的位移向量uk。定义双线性插值算子

(2)

1.3 前光滑过程
细网格下的方程组表示为
{Kk}u(t+Δt)={Qt+Δt}.
(3)

1.4 粗网格修正过程

}.
(4)
2)限制残量。利用限制算子以减少误差影响,通过对细网格的限制
}.
(5)
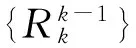
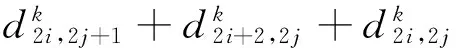
(6)
3)误差求解。对于误差,同样需要进行解算、插值、迭代的计算过程。通过求解粗网格下的方程组
{Kk-1}{vk-1}={dk-1}
(7)
获取粗网格下解的误差vk-1。误差的求解同样也采用高斯-赛德尔迭代方法。

(8)
5)细网格校正。最后对k层网格进行精确校正
(9)
1.5 后光滑过程
综上所述,多重网格算法可描述如下:
1)计算粗网格初始位移;
2)插值计算细网格位移初值;
3)迭代解算细网格位移向量;
4)位移修正;
5)后光滑消除高频误差。
为使结果更加真实可靠,初始网格位移必须相对精确,本文使用长期观测的GPS观测站观测结果检核初始网格节点位移。
2 算例分析
本文利用Fortran语言编程,通过算例进行分析。
算例:如图1所示,结构上部y方向固定和右部上半部x方向固定,每单元横向跨度为5 m,纵向为4 m,厚度为0.5 m,介质弹性模量为90 GPa,泊松比为0.25,密度为2 750 kg/m3,粘滞系数为5.0×1021Pa·s,左侧加载向右荷载P=10 MPa。加载时间长度为10 s,步长Δt=0.004 s。本文采用弹性模型进行计算,A点假设当时间为t=2 s时发生断裂,断裂带发生右旋走滑,滑动量为2.5e-4 m。

图1 算例示意图


图2 有限元直接解算位移场和最大主应力场
本文利用Fortran语言编程,分别利用普通有限元法和多重网格有限元方法对模型进行计算,得到位移场和应力场,并进行对比。
模型计算得到的位移场及应力场如图2~4所示。在多重网格计算过程中,首先将结构划分为较大单元,利用有限元法直接解算位移,将其作为初始网格位移。为更为细致研究结构各部分对荷载的动力响应,利用多重网格方法将各个单元进一步细分。
以图1中A点为例,以结构力学解析解作为真值[6],比较有限元直接解算结果与多重网格解算结果见表1。

表1 结果比较(Δt=0.004 s)

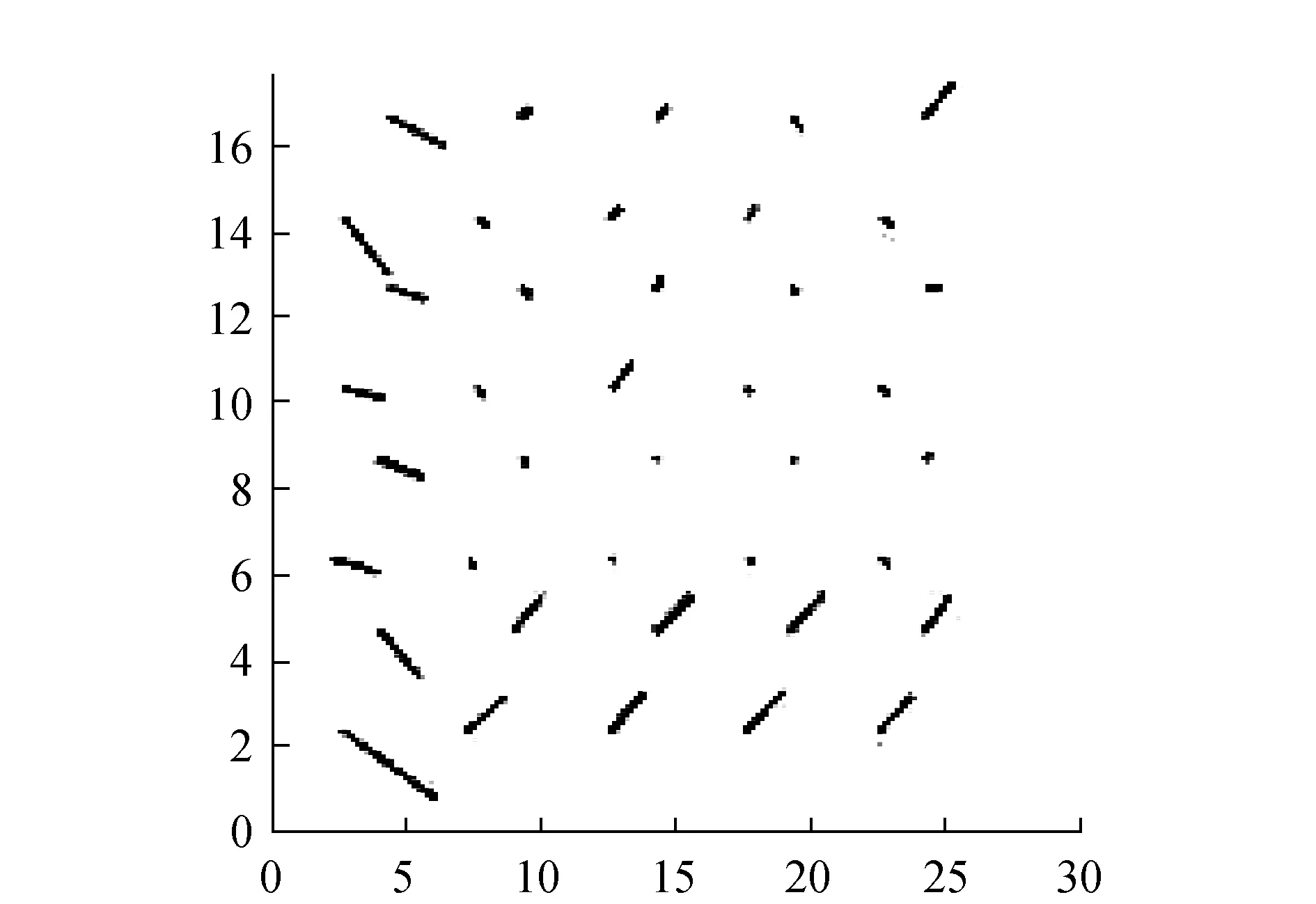
图3 多重网格初始网格位移场和最大主应力场

从表1中可以看出,有限元直接解误差并不稳定,而多重网格解误差随着时间的增加逐渐降低。因此,使用多重网格求解动力模型有其精度上的优势。
3 结 论
通过以上研究,本文得出以下结论:
1)针对有限元方法运算量较大,大量网格往往需要专业软件进行解算的问题,本文提出了多重网格解算方法,以数量较少的初始网格直接采用有限元解算,然后通过细分网格,采用迭代方法就可以实现大量网格的解算,大大简化了运算量,可以自主编程实现;
2)随着时间的增加,多重网格精度逐渐提高,而有限元解则没有明显提高,显示出多重网格具有降噪、提高精度的优势;
3)实际解算中,多重网格的运用可以非常灵活,既可以对整个结构进行细分,也可以对某一大单元进行细分,计算简便且精度较高。
综上所述,多重网格方法的引入,为地壳运动和形变的研究提供了一个有用的工具。
[1]党亚民,晁定波,许才军,等.利用GPS形变资料确定地壳形变的应变特征[J].测绘科学,2001,26(3):10-13.
[2]党亚民,陈俊勇,张燕平,等.利用GPS资料分析南天山地区的地壳形变特征[J].测绘科学,2002,27(4):13-15.
[3]张东宁,许忠淮.中国大陆岩石层动力学数值模型的边界条件[J].地震学报,1999,21(2):133-139.
[4]ZHANG J.Accelerated multigrid high accuracy solution of the convection diffusion equation with high Reynolds number[J].Numerical Methods for Partial Differential Equations,1997,13:77-92.
[5]张淼.结构动力响应分析多重网格方法研究[D].长春:吉林大学,2008.
[6]张森文,曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报,2000,17(1):94-97.
[7]杨强,党亚民.利用GPS速度场估算青藏高原地壳韧性层等效粘滞系数分布的研究[J].测绘学报,2010,39(5):497-502.
[责任编辑:刘文霞]
Researchonthesolutiontothedynamicequationwithmultigridmethod
YANG Qiang1,DANG Ya-min1,ZHAO Wen-jiao1,2,DU Bin1,2
(1.Chinese Academy of Surveying and Mapping,Beijing 100830,China; 2.Shandong University of Science and Technology,Qingdao 266590,China)
The method is introduced. Multigri mothod is used during solving the dynamic equations,of which the several times iterative and gradual grid subdivision are used to simplify the calculation of FEM.Its case analysis shows the multigrid method has the advantages of using flexibly,reducing operand,simplifying calculation and restraining noise.The introduction of multi-grid method provides a useful tool for the study of crustal movement and deformation.
multigrid;finite element;dynamic equation;iterative method
2012-09-11
杨 强(1975-),男,博士.
P227
:A
:1006-7949(2014)01-0017-04

