基于EKF和自适应抗差滤波的星载GPS定轨方法
段 宇,吴江飞
(信息工程大学 地理空间信息学院,河南 郑州 450052)
基于EKF和自适应抗差滤波的星载GPS定轨方法
段 宇,吴江飞
(信息工程大学 地理空间信息学院,河南 郑州 450052)
针对在星载GPS卫星定轨中由于卫星动力学模型误差和不可避免的观测异常严重影响定轨精度的问题,通过采用适当的自适应控制因子和应用抗差估计原理,构造自适应抗差扩展卡尔曼滤波(RAEKF)来实现星载GPS卫星定轨。实测计算表明,自适应抗差扩展卡尔曼滤波对观测误差和状态扰动有一定的抵制能力,与一般扩展卡尔曼滤波相比提高了精度,证明其理论的可行性。
非线性滤波;定轨;扩展卡尔曼滤波;自适应滤波;抗差估计
国内外学者提出多种自适应滤波算法并广泛地应用于各种工程实践中[1-3]。利用抗差估计原理也可以实现动态系统的自适应滤波[3]。卡尔曼滤波应用于星载GPS实时定轨的情况下,由于一方面低轨卫星的受力情况复杂,其动力学模型的精确度难以保证。另一方面其数据采集装置星载GPS接收机处在外空高速运动状态,环境变换大,可观测性不强。这些特点导致星载GPS观测值出现异常甚至粗差的几率与地面观测的情形相比有明显的增大。上述问题若无法解决,卡尔曼滤波结果的精确性和稳定性会显著降低,严重情况下甚至会导致滤波器的发散。因此,在使用卡尔曼滤波器进行迭代计算时,对于状态噪声协方差矩阵和观测噪声协方差阵采用抗差估计的原理自适应的求解,可以有效地减弱和控制观测噪声和状态噪声对状态估计的影响[4-5]。
EKF(extended Kalman filter)是一种非线性滤波算法。它是在卡尔曼滤波的框架下,使用展开泰勒级数的方法对动态方程和误差方程作一阶线性化处理,来近似非线性滤波的方法[6]。它是到目前为止应用最为广泛的一种非线性滤波,且在某些情况下仍为解决问题的最佳方法[7-8]。本文基于非线性滤波EKF研究了一种新的非线性自适应抗差滤波(adaptively robust extended Kalman filter, AREKF),并将这种算法在MicroLab-1卫星的精密定轨中进行应用,实测计算结果证明该算法的有效性和可行性。
1 非线性自适应抗差滤波[9]
本文研究的卫星轨道确定问题是一个非线性系统。非线性系统的状态方程和观测方程分别为
Xk=f(Xk-1)+Wk,
(1)
Lk=h(Xk)+ek.
(2)
式中:Xk为状态向量;f(·)为状态转移方程;Wk为状态噪声向量;Lk为观测向量;h(·)为观测方程;ek为观测噪声向量。其中Wk和ek的期望为零,且不相关,协方差分别为∑Wk和∑k。
为控制观测异常和状态噪声导致的状态预测信息异常对状态参数估值的影响,可以构造如下极值原则:
n.
(3)
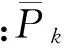
对式(3)求极值可得
).
(4)
在扩展卡尔曼滤波框架下,式(4)可等价为
).
(5)
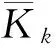
(6)
状态向量验后协方差矩阵为
(7)
由以上公式可得,要实现自适应抗差滤波,就必须求得观测向量等价协方差矩阵和自适应因子。
1.1 观测噪声等价协方差阵[3]
观测向量等价协方差阵可通过双因子方差膨胀模型求得[9]。观测向量的协方差矩阵是一种观测量的精度评定指标,它能够定量地反映观测量的离散程度。如果观测向量等价协方差小,则说明观测量的质量好,精度高,该观测所占的权重就大;相反地,若观测量的质量较低,精度一般,则该观测所占的权重就小。

(8)

由此生成的协方差矩阵称为等价协方差矩阵。由上述推导可以知道,通过加入膨胀因子构造的等价协方差阵仍然能够与原来的协方差阵保持相关性。
为了在观测误差超过阈值时,相应的方差膨胀,否则原有的方差不变,以λii为例,其膨胀因子可构造为
(9)

(10)
式中:vi,σvi分别为残差向量Vk和残差向量协方差矩阵∑Vi中的元素。可由以下公式求得
(11)
(12)
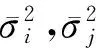
由膨胀因子的构造过程可以得知,当观测值的误差超过某一设定值时,相应的方差会膨胀,即对原协方差矩阵作降权处理。反之,膨胀因子的值为1,原方差保持不变。
1.2 自适应因子
不同的误差判别统计量[10]或衡量了动态载体实时位置状态与模型标定状态的差异,或衡量了动力学模型的误差大小。基于这样的原理,可以构造自适应因子α,以调节状态信息与观测信息对参数估计的影响。本文中选择了两段函数模型作为自适应因子,其具体形式为
(13)
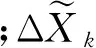
(14)
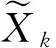
(15)
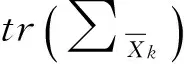
1.3 非线性自适应抗差扩展卡尔曼滤波算法
以标准EKF算法框架为基础,结合1.1、1.2所述理论,可以建立如下的非线性自适应抗差卡尔曼滤波算法:
状态更新:
(16)
(17)
量测更新:
(18)
(19)
(20)

2 计算与分析
为了验证所提出的算法性能,实验中选取MicroLab-1卫星星载GPS接收机所采集的数据进行定轨解算[11]。在数据处理时进行了一定的简化。本算例使用了预测残差统计量作为误差判别统计量,采用两段式函数构成自适应因子。对于膨胀因子和预测残差统计量的阈值选取,经过多次计算和比较,确定为0.9和0.8。
本算例中为研究自适应抗差滤波的性能,设置了A,B,C 3种情况,其参数设置如表1所示;同时将24 h内分别由标准扩展Kalman滤波(EKF)和抗差自适应Kalman滤波(RAEKF)计算的位置误差和速度误差绘制成图,如图1~6所示。

表1 A,B,C 3种情况下的滤波参数

图1 情况A的位置误差

图2 情况A的速度误差

图3 情况B的位置误差

图4 情况B的速度误差

图5 情况C的位置误差

图6 情况C的位置误差
由图1~6可以得出:
1)滤波结果在前5 000 s 历元内极不稳定,位置误差最大约达180 m,速度误差最大达0.29 m/s,其后趋于稳定,这是由滤波的原理造成的;
2)自适应抗差滤波相对于EKF的滤波结果有所改善,大部分历元的误差均有所降低,但误差仍在同一个数量级;
3)从自适应抗差滤波结果相对EKF滤波结果的改善情况来看,情况B改善最大,误差减小幅度最大,情况A次之,情况C基本无明显改善,说明状态噪声的权越大,自适应抗差滤波的效果越明显。
均方根误差(RMS)是估值与真值之差的平方与观测次数比值的平方根,能很好地反应出估值的精度。本算例中,分别计算了状态向量估值各维的均方根误差和位置、速度均方根误差。其中位置分量的均方根误差[12]计算公式为

(21)

(22)
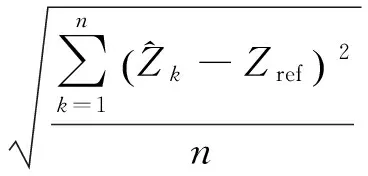
(23)

(24)
速度分量的均方根误差计算公式依此类推。其计算结果如表2所示。
表2给出了A,B,C 3种方案的RMS误差统计结果。可以看出,AREKF的轨道确定结果在各个分量上的RMS误差均小于EKF的轨道确定结果在各个分量上的RMS误差。各种情况的自适应抗差滤波结果的均方根误差相对于EKF均有所减小,说明估值的精度均有所提高,但并不十分明显,其中,情况B精度提高最大,情况A次之,情况C精度提高最小。这与上图的分析是一致的。
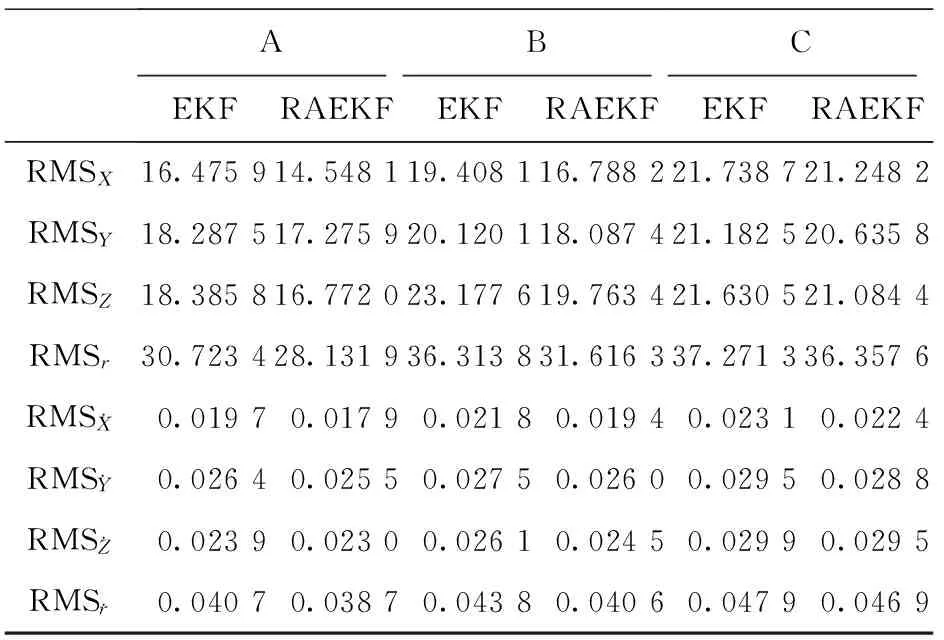
表2 A,B,C 3种方案的RMS误差统计结果 m
3 结束语
结合上一节的图表可知,个别历元自适应抗差滤波的解反而比EKF解的误差更大。这一方面是因为原始观测数据误差较大,无论使用何种滤波方法均不可能实现高精度的定轨,另一方面因为自适应抗差滤波只是修改了观测噪声协方差阵和预测状态协方差阵,只能消减观测误差和状态噪声的扰动对滤波结果的影响,提升总体滤波精度,并不能使每个历元的误差都降低。总的来说,本文提出的自适应抗差扩展卡尔曼滤波算法(RAEKF)对状态扰动和观测误差有一定的抵制能力,与标准扩展卡尔曼滤波(EKF)相比提高了精度,证明其理论的可行性。
[1]YANG YUANXI,HE HAIBO,XU GUOCHANG. Adaptively Robust Filtering for Kinematic Geodetic Position[J]. Journal of Geodesy,2001,75(2):109-116.
[2]杨元喜,何海波,徐天河. 论动态自适应滤波[J]. 测绘学报,2001,30(4):293-298.
[3]杨元喜,文援兰. 卫星精密轨道综合自适应抗差滤波技术[J]. 中国科学(D辑),2003,33(11):1 112-1 119.
[4]陈蕾,刘立龙,陈东银. 自适应卡尔曼滤波法用于变形监测数据处理[J]. 测绘工程,2008,17(1):48-54.
[5]李勇军,左娟. GPS动态定位自适应卡尔曼滤波算法研究[J]. 测绘工程,2012,21(4):30-32.
[6]吴江飞. 星载GPS卫星定轨若干问题的研究[D]. 上海:中国科学院上海天文台,2006:100-101.
[7]郭雪姣. 非线性滤波算法研究及其在卫星高精度定轨中的应用[D]. 长沙:国防科技大学,2010:23-24.
[8]吴江飞,雷辉,王世忠. 一种新型非线性滤波理论及其应用[J]. 测绘工程,2008,17(6):16-19.
[9]吴江飞,黄珹. 非线性自适应抗差滤波定轨算法研究[J]. 武汉大学学报:信息科学版,2008,33(2):187-190.
[10]杨元喜. 自适应动态导航定位[M]. 北京:测绘出版社,2006.
[11]OLIVER MONTENBRUCK,EBERHARD GILL. Satellite Orbits[M]. Berlin:Springer-Verlag,Germany,2000:297.
[12]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉:武汉大学出版社,2003.
[责任编辑:刘文霞]
Methodofsatellite-borneGPSorbitdeterminationbasedonEKFandadaptiverobustfilter
DUAN Yu, WU Jiang-fei
(School of Geospatial Information, Information Engineer University, Zhengzhou 450052, China)
The satellite dynamic model errors and the inevitable observation anomaly have a serious influence on the orbit determination accuracy of satellites based on GPS. An appropriate adaptive control factor and the robust estimation theory are used to establish an adaptive robust extended Kalman filter(AREKF) to complete the orbit determination of satellites based on GPS. The measured calculation shows that the adaptive robust extended Kalman filter serves a certain resistance against the observation error and state disturbance. The precision is improved and the feasibility of the theory compared with the standard extended kalman filter is verified.
nonlinear filter; orbit determination; EKF; adaptive filter; robust estimation
2013-03-19
国家自然科学基金资助项目(41174006;40974010;41274016)
段 宇(1989-),男,硕士研究生.
P228.4
:A
:1006-7949(2014)01-0021-04

